Phasenraum
Der Phasenraum beschreibt die Menge aller möglichen Zustände eines dynamischen Systems. Ein Zustand wird durch einen Punkt im Phasenraum eindeutig abgebildet. In der Mechanik besteht er aus verallgemeinerten Koordinaten (Konfigurationsraum) und zugehörigen verallgemeinerten Geschwindigkeiten (siehe Prinzip der virtuellen Leistung).
Hauptteil[Bearbeiten | Quelltext bearbeiten]
Bei Freiheitsgraden (Anzahl generalisierter Koordinaten oder Ortskoordinaten) ist der Phasenraum -dimensional. Beispielsweise hat ein Gasteilchen im dreidimensionalen Raum Freiheitsgrade, mit den zugehörigen Impulsen sind das Phasenraumkoordinaten. Ein System (Gas) von Teilchen hat einen -dimensionalen Phasenraum. Es werden aber auch Phasenräume in anderen Anwendungen außerhalb der Mechanik untersucht.
Die zeitliche Entwicklung eines Punktes im Phasenraum wird durch Differentialgleichungen beschrieben und durch Trajektorien (Bahnkurven, Orbit) im Phasenraum dargestellt. Diese sind durch Differentialgleichungen erster Ordnung in der Zeit beschrieben und durch einen Anfangspunkt eindeutig festgelegt (ist die Differentialgleichung zeitunabhängig, sind dies autonome Differentialgleichungen). Dementsprechend kreuzen sich zwei Trajektorien im Phasenraum auch nicht,[1] da an einem Kreuzungspunkt der weitere Verlauf nicht eindeutig ist. Geschlossene Kurven beschreiben oszillierende (periodische) Systeme.

Für Systeme mit bis zu drei Variablen kann der Phasenraum graphisch dargestellt werden. Insbesondere für zwei Variable kann man so die Bewegung (Trajektorien, Phasenraumfluss als Vektorfeld) in einem Phasenraumporträt oder Phasenporträt anschaulich darstellen und qualitativ analysieren (Phasenraumanalyse, Nullklinen und Fixpunkte).
Der historische Ursprung der Verwendung von Phasenräumen wird häufig auf Joseph Liouville zurückgeführt – wegen des Satzes von Liouville (1838), dass bei konservativen Systemen (mit Energieerhaltung) das Phasenraumvolumen benachbarter Trajektorien zeitlich konstant ist. Liouville hatte aber kein mechanisches System im Auge, sondern bewies den Satz für allgemeine gewöhnliche Differentialgleichungen erster Ordnung, die Verbindung zur Mechanik schlug erst Carl Gustav Jacobi vor.[2] Das Phasenraumkonzept entstand erst, nachdem im weiteren Verlauf des 19. Jahrhunderts die Mathematiker zur Betrachtung höherdimensionaler Räume übergingen. Die erste Verwendung des Phasenraums im heutigen Sinn war bei Ludwig Boltzmann 1872[3] im Rahmen seiner Untersuchungen der statistischen Mechanik, was 1879 von James Clerk Maxwell übernommen wurde[4]. Das Konzept fand dann Verwendung in den Vorlesungen von Boltzmann und Josiah Willard Gibbs zur statistischen Mechanik, im Artikel zur statistischen Mechanik in der Enzyklopädie der mathematischen Wissenschaften von 1911 von Paul Ehrenfest und Tatjana Ehrenfest (die die Bezeichnung für den Phasenraum einführten) und in der qualitativen Theorie der Differentialgleichungen durch Henri Poincaré.
Ein dynamisches System, dessen Trajektorien den gesamten Phasenraum ausfüllen, also jedem Punkt im Phasenraum beliebig nahekommen, nennt man ergodisch, siehe auch Ergodenhypothese. Bei konservativen mechanischen Systemen (abgeschlossenen Systemen) ist nach dem Satz von Liouville das Phasenraumvolumen benachbarter Trajektorien zeitlich konstant, bei dissipativen Systemen nimmt es ab (offene Systeme).
In der hamiltonschen Mechanik ist der Phasenraum ein Beispiel für eine symplektische Geometrie und die hamiltonsche Mechanik nach den Worten von Wladimir Arnold ist die Geometrie des Phasenraums[5]. Da die Impulse als Ableitungen der Hamiltonfunktion nach den generalisierten Koordinaten definiert sind, ist der Phasenraum dort ein Kotangentialbündel über dem Konfigurationsraum.
In der Quantenmechanik drückt die Heisenbergsche Unschärferelation eine Quantisierung des Phasenraums aus. In der älteren Quantentheorie erfolgt dies durch die Bohr-Sommerfeld-Quantisierung. Übergänge von Verteilungsfunktionen vom klassischen zum quantenmechanischen Phasenraum (und umgekehrt) liefern die Wigner-Funktion und Weyl-Quantisierung.
Beispiel einer Phasenraumanalyse[Bearbeiten | Quelltext bearbeiten]
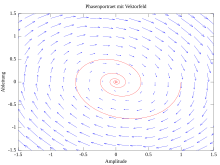

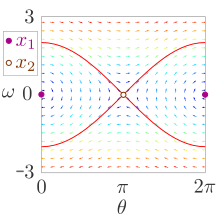
Das Phasenraumporträt gibt eine Möglichkeit, die zeitlichen Entwicklungen dynamischer Systeme graphisch zu analysieren. Dazu werden nur die dynamischen Gleichungen des Systems benötigt, eine explizite Darstellung der Zeitentwicklung, etwa durch analytisches Lösen einer Differentialgleichung, ist nicht nötig.
Als Beispiel folgen einige Elemente der Phasenraumanalyse in einem zweidimensionalen System , das durch die Differentialgleichungen (, )
beschrieben ist:
- Einzeichnen des Vektorfelds der Dynamik: Für ein Raster von Punkten wird die Richtung der Bewegung im Phasenraum durch Pfeile dargestellt. Folgt man nun ausgehend von einem bestimmten Startpunkt dem Pfeil, kommt man zu einem neuen Punkt, wo man dieses Vorgehen wiederholen kann. So kann man anhand des Vektorfelds zusätzlich typische Trajektorien in das Phasenraumporträt einzeichnen, die das qualitative Verhalten der zeitlichen Entwicklung einzuschätzen helfen. Beim van-der-Pol-Oszillator zum Beispiel laufen alle Trajektorien auf einen Grenzzyklus zu, was sich anhand von Beispieltrajektorien innerhalb und außerhalb des Zyklus illustrieren lässt. Für einfache dynamische Systeme kann man Vektorfeld und Beispieltrajektorien oft mit der Hand einzeichnen, bei komplexeren Systemen kann dies durch Computerprogramme geschehen.
- Einzeichnen der Nullklinen: Eine Nullkline bezeichnet eine Kurve im Phasenraum, entlang der sich eine der dynamischen Variablen nicht ändert. Im Fall des obigen zweidimensionalen Systems ist die x-Nullkline durch die Bedingung und die y-Nullkline durch definiert. Diese Gleichungen lassen sich häufig auch dann nach einer der Variablen auflösen, wenn die Gesamtdynamik nicht analytisch integriert werden kann.
- Bestimmen von Fixpunkten und ihrer Stabilität: Als Fixpunkte werden Zustände bezeichnet, die sich mit der Zeit nicht ändern. Solche Fixpunkte entsprechen den Kreuzungspunkten der Nullklinen im Phasenraum. Im obigen zweidimensionalen System erklärt sich das dadurch, dass an so einem Kreuzungspunkt die Bedingung erfüllt ist. Durch eine lineare Stabilitätsanalyse kann auch bestimmt werden, ob Trajektorien in der Nähe dieser Punkte angezogen oder abgestoßen werden.
- Finden von Separatrizen: Als Separatrix (abgeleitet von lat. separare „trennen“) wird eine Kurve bzw. (Hyper-)Fläche bezeichnet, die Phasenraumgebiete mit unterschiedlichem (Langzeit-)Verhalten voneinander trennt.[6] Gibt es beispielsweise zwei Fixpunkte, die Trajektorien anziehen, gibt es unter Umständen eine Separatrix, die die beiden Einzugsbereiche voneinander trennt. Mit den Orten und der Stabilität aller Fixpunkte bzw. mit dem Vektorfeld der Dynamik können in geeigneten Fällen die Separatrizen ohne weitere Berechnungen gefunden werden.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Zustandssumme
- Zustandsraum (Mechanik), Erweiterung des Phasenraums um die Zeit
- Diskussion von Fixpunkten bei Autonome Differentialgleichung
- Impulsraum, Unterraum des Phasenraums
- Ergebnisraum, die Menge aller möglichen Ergebnisse eines Zufallsexperiments
Literatur[Bearbeiten | Quelltext bearbeiten]
- Y. S. Kim, W. W. Zachary (Hrsg.): The physics of phase space., Proc. First Int. Conf. Physics Phase Space, College Park, Maryland 1986, Lecture Notes in Physics 278, Springer, Berlin 1987, ISBN 3-540-17894-5.
- Cosmas K. Zachos: Quantum mechanics in phase space – an overview with selected papers. World Scientific, Singapore 2005, ISBN 978-981-238-384-6.
- V. Arnold: Mathematical methods of classical mechanics. Springer 1989.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- State space. In: Scholarpedia.org. (Englisch, inkl. Literaturangaben).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Es kann allerdings der Fall auftreten, dass im Phasenraumporträt zwei Kurven einander schneiden wie die Separatrix beim Pendel, der Kreuzungspunkt wird aber bei der Bewegung auf Trajektorien des Systems nicht erreicht.
- ↑ David Nolte: The tangled tale of phase space. In: Physics Today. April 2010, S. 33.
- ↑ Ludwig Boltzmann: Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. In: Sitz.-Ber. Akad. Wiss. Wien (II). Band 66, 1872, S. 275–370.
- ↑ James Clerk Maxwell: On Boltzmann’s Theorem on the average Distribution of Energy in a System of Material Points. In: Transactions of the Cambridge Philosophical Society. Band 12, 1879, S. 547–570 (hathitrust.org).
- ↑ Arnold: Mathematical methods of classical mechanics. Springer, 1989, S. 161.
- ↑ Steven H. Strogatz: Nonlinear Dynamics And Chaos. Westview Press, 2000, ISBN 978-0-7382-0453-6, S. 159.



















