Ornstein-Uhlenbeck-Prozess

Der Ornstein-Uhlenbeck-Prozess (oft abgekürzt OU-Prozess oder noch kürzer O-U) ist ein spezieller stochastischer Prozess, welcher nach den beiden niederländischen Physikern George Uhlenbeck (1900–1988) und Leonard Ornstein (1880–1941) benannt ist. Er ist neben der geometrischen Brownschen Bewegung einer der einfachsten und gleichzeitig wichtigsten über eine stochastische Differentialgleichung definierten Prozesse. Im Vasicek-Modell zur Zinssatzmodellierung werden Ornstein-Uhlenbeck-Prozesse verwendet.
Definition und Parameter[Bearbeiten | Quelltext bearbeiten]
Seien und Konstanten. Ein stochastischer Prozess heißt Ornstein-Uhlenbeck-Prozess mit Anfangswert , Gleichgewichtsniveau , Steifigkeit und Diffusion , wenn er das folgende stochastische Anfangswertproblem löst:
- ,
wobei ein Standard-Wienerprozess ist.
Die Parameter lassen sich einfach interpretieren und somit bei der Modellierung einer stochastischen Zeitreihe einfach als „Stellschrauben“ verwenden:
- ist das gleichgewichtige Niveau des Prozesses (englisch: mean reversion level). Liegt über diesem Wert, so ist der Driftterm negativ, und die Drift wird den Prozess tendenziell nach unten „ziehen“. Ist kleiner, so ist die Drift positiv und der Prozess wird in Erwartung nach oben gezogen.
- (englisch mean reversion speed oder mean reversion rate) gibt an, wie stark die oben beschriebene „Anziehungskraft“ von ist. Für kleine Werte von verschwindet dieser Effekt, für große Werte wird sich sehr steif um entwickeln.
- gibt an, wie stark der Einfluss von (also des Zufalls) auf den Prozess ist. Für wird einfach exponentiell gegen konvergieren, bei starker Diffusion wird diese Konvergenz zufällig gestört.
Der Unterschied zum ebenfalls mit dem mean-reversion-Mechanismus ausgestatteten Wurzel-Diffusionsprozess oder der geometrischen Brownschen Bewegung besteht im Wesentlichen darin, dass beim OU-Prozess der Diffusionsterm konstant, also unabhängig von ist. Dies führt dazu, dass der OU-Prozess im Gegensatz zu den anderen beiden auch negative Werte annehmen kann.
Lösung der Differentialgleichung[Bearbeiten | Quelltext bearbeiten]
Im Gegensatz zum Wurzel-Diffusionsprozess ist die obige Differentialgleichung explizit lösbar, wenn auch nicht (wie bei der geometrischen brownschen Bewegung) integralfrei darstellbar: Mit der Lösung der zugehörigen homogenen Gleichung führt Variation der Konstanten auf den Ansatz , also . Wendet man auf die Funktion einerseits die Itō-Formel, andererseits die gewöhnliche Kettenregel der Differentialrechnung an, so erhält man
- .
Die obige Identität von 0 bis aufintegriert (wobei ) ergibt die Lösung
- .
Eigenschaften[Bearbeiten | Quelltext bearbeiten]

- Ein Ornstein-Uhlenbeck-Prozess ist ein Gauß-Prozess. Dies erkennt man an der obigen Lösung: Der Integrand ist deterministisch, also ist der Wert des Ito-Integrals stets normalverteilt. Wie für jeden Gauß-Prozess ist die Verteilung des Ornstein-Uhlenbeck-Prozesses durch seine Erwartungswert- und Kovarianzfunktion eindeutig bestimmt. Diese ergeben sich als
- und
- .
- Die univariaten Verteilungen der für sind Normalverteilungen:
- .
- Ein Ornstein-Uhlenbeck-Prozess mit nichtstochastischem Anfangswert besitzt eine konstante Erwartungswertfunktion im Fall .
- Ein Ornstein-Uhlenbeck-Prozess mit nichtstochastischem Anfangswert ist nicht stationär, wie man an der Kovarianzfunktion erkennt, die nicht nur von der Zeitdiffererenz abhängt. Mit stochastischem Anfangswert existiert ein stationärer Ornstein-Uhlenbeck-Prozess, siehe weiter unten.
- Ein Ornstein-Uhlenbeck-Prozess ist ein gaußscher Markow-Prozess.
- Ein Ornstein-Uhlenbeck-Prozess ist – wie auch der Wurzel-Diffusionsprozess – ein affiner Prozess.
- Ein Ornstein-Uhlenbeck-Prozess entspricht einem Tiefpass-gefilterten weißen Rauschen mit einem linearen IIR-Tiefpassfilter 1. Ordnung mit Grenzfrequenz .[1] Sein Spektrum ist daher für niedrige Frequenzen flach, wie beim weißen Rauschen, und für hohe Frequenzen proportional zu 1/f², wie beim roten Rauschen. Im Gegensatz zum rein weißen und roten Rauschen ist das Spektrum des Ornstein-Uhlenbeck-Prozess damit quadratintegrierbar, und der Prozess besser als ideales weißes oder rotes Rauschen auf physikalische Situationen anwendbar, die grundsätzlich amplituden-, bandbreiten und leistungslimitiert sind.
- Ein Ornstein-Uhlenbeck-Prozess entspricht auch einem Hochpass-gefilterten Wiener-Prozess mit einem linearen IIR-Hochpassfilter 1. Ordnung mit Grenzfrequenz (siehe Abbildung). Dies geht direkt aus der Definition hervor, die zu einem bestehenden Wiener-Prozess den linearen Filterterm addiert, der tiefe Frequenzkomponenten dämpft. Im Gegensatz zum skaleninvarianten Wiener-Prozess besitzt der Ornstein-Uhlenbeck-Prozess damit eine Zeitskala und ist in dieser Hinsicht komplizierter. Für Zeitskalen deutlich kleiner als 1/θ kann der Ornstein-Uhlenbeck-Prozess jedoch durch den Wiener-Prozess approximiert werden. Es gilt im Sinne der Verteilungskonvergenz[2]
Stochastischer Anfangswert und stationärer Ornstein-Uhlenbeck-Prozess[Bearbeiten | Quelltext bearbeiten]
Ein Ornstein-Uhlenbeck-Prozess mit stochastischen Anfangswert ist
- .
Erwartungswert- und Kovarianzfunktion[Bearbeiten | Quelltext bearbeiten]
Ein Ornstein-Uhlenbeck-Prozess mit stochastischen Anfangswert hat die auf den Anfangswert bedingte Erwartungswertfunktion
und die auf den Anfangswert bedingte Kovarianzfunktion
Hieraus ergeben sich mit die (unbedingte) Erwartungswertfunktion
und mit die (unbedingte) Kovarianzfunktion
Die weiter oben angegebenen Erwartungswert- und Kovarianzfunktionen für einen Ornstein-Uhlenbeck-Prozess mit nichtstochastischem Anfangswert erhält man als Spezialfall für und .
Stationarität[Bearbeiten | Quelltext bearbeiten]
Da ein Ornstein-Uhlenbeck-Prozess ein Gauß-Prozess ist, fallen die Konzepte der Stationarität im engeren Sinn und der Stationarität im weiteren Sinn zusammen.
Für den speziellen stochastischen Startwert mit
erhält man einen stationären Ornstein-Uhlenbeck-Prozess mit der Erwartungswertfunktion
und der Kovarianzfunktion
Alle Zufallsvariablen des stationären Ornstein-Uhlenbeck-Prozess haben dieselbe univariate Wahrscheinlichkeitsverteilung
Stabilität[Bearbeiten | Quelltext bearbeiten]
Der stationäre Ornstein-Uhlenbeck-Prozess kann durch folgende Stabilitätseigenschaft ergänzt werden. Für jeden Ornstein-Uhlenbeck-Prozess mit nichtstochastischem Startwert gilt
und
Da die Verteilungen von Gauß-Prozessen durch ihre Erwartungswert- und Kovarianzfunktion festliegen, bedeutet dies, dass sich alle Ornstein-Uhlenbeck-Prozesse, die mit nichtstochastischem Anfangswert starten, für fortschreitende Zeit dem stationären Ornstein-Uhlenbeck-Prozess mit der Erwartungswertfunktion und der Kovarianzfunktion annähern.
Lévy-Prozesse[Bearbeiten | Quelltext bearbeiten]
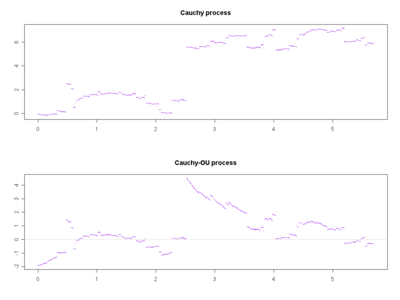
Wird die definierende Differentialgleichung von einem anderen Lévy-Prozess als der brownschen Bewegung angetrieben, so erhält man auch einen (nicht-gaußschen) Ornstein-Uhlenbeck-Prozess.
Literatur[Bearbeiten | Quelltext bearbeiten]
- G. E. Uhlenbeck, L. S. Ornstein: On the Theory of the Brownian Motion. In: Physical Review. 36. Jahrgang, Nr. 5, 1. September 1930, ISSN 0031-899X, S. 823–841, doi:10.1103/PhysRev.36.823 (englisch).
- Daniel T. Gillespie: Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. In: Physical Review E. 54. Jahrgang, Nr. 2, 1. August 1996, ISSN 1063-651X, S. 2084–2091, doi:10.1103/PhysRevE.54.2084, PMID 9965289 (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Enrico Bibbona, Gianna Panfilo, Patrizia Tavella: The Ornstein–Uhlenbeck process as a model of a low pass filtered white noise. In: Metrologia. 45. Jahrgang, Nr. 6, 5. Dezember 2008, ISSN 0026-1394, S. S117–S126, doi:10.1088/0026-1394/45/6/S17 (englisch).
- ↑ L. C. G. Rogers and D. Williams: Diffusions, Markov Processes and Martingales. Vol. 1. Cambridge University Press, Cambridge, 2000, S. 54.
























![{\displaystyle \mathrm {E} [X_{t}]=ae^{-\theta t}+\mu (1-e^{-\theta t}),\quad t\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82dd468b22179492551f4f1f74b03c0890a7190e)
![{\displaystyle \operatorname {Cov} [X_{s},X_{t}]={\frac {\sigma ^{2}}{2\theta }}\,(e^{-\theta |s-t|}-e^{-\theta (s+t)}),\quad s,t\geq 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab287aa071659b3c30ccd640647a291404db6d4)










![{\displaystyle \mathrm {E} [X_{t}|X_{0}]=X_{0}e^{-\theta t}+\mu (1-e^{-\theta t}),\quad t\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7cacf0a1ae948909dbcb453f099525484648dc4)
![{\displaystyle \operatorname {Cov} [X_{s},X_{t}|X_{0}]={\frac {\sigma ^{2}}{2\theta }}\,(e^{-\theta |s-t|}-e^{-\theta (s+t)}),\quad s,t\geq 0\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63475cdd8fbae3434cd47042d504659fc6f4b415)
![{\displaystyle \mathrm {E} [X_{t}]=\mathrm {E} [\mathrm {E} [X_{t}|X_{0}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae858216a275f104e89ea39826b96833ac07d98)
![{\displaystyle \mathrm {E} [X_{t}]=\mu _{0}e^{-\theta t}+\mu (1-e^{-\theta t}),\quad t\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9cdee4372176a1ea5206e2c57c8dc2dd982fdae)
![{\displaystyle \mathrm {Cov} [X_{s},X_{t}]=\mathrm {E} [\mathrm {Cov} [X_{s},X_{t}|X_{0}]]+\mathrm {Cov} [\mathrm {E} [X_{s}|X_{0}],\mathrm {E} [X_{t}|X_{0}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e76060e6d89fb0ea4d92517749e29b76924ae48)
![{\displaystyle \operatorname {Cov} [X_{s},X_{t}]={\frac {\sigma ^{2}}{2\theta }}\,(e^{-\theta |s-t|}-e^{-\theta (s+t)})+\sigma _{0}^{2}e^{-\theta (s+t)}\quad s,t\geq 0\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9aa46130db4acf14d7f301ed636fcf3ac69eb4e)




![{\displaystyle \mu ^{*}(t):=\mathrm {E} [X_{t}]=\mu ,\quad t\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62f2110d9c9a36460d32c0e8d5e19008d5df3663)
![{\displaystyle \gamma ^{*}(s,t):=\mathrm {Cov} [X_{s},X_{t}]={\frac {\sigma ^{2}}{2\theta }}e^{-\theta |s-t|},\quad s,t\geq 0\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36eb3e8dd15b3c482a6be5111cfd54bd46667a31)

![{\displaystyle \lim _{t\to \infty }|\mathrm {E} [X_{t}]-\mu ^{*}(t)|=\lim _{t\to \infty }\left|ae^{-\theta t}+\mu (1-e^{-\theta t})-\mu \right|=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e7f4329f30c6721a009120a293a83322d5737d)
![{\displaystyle \lim _{\min\{s,t\}\to \infty }|\mathrm {Cov} [X_{s},X_{t}]-\gamma ^{*}(s,t)|=\lim _{\min\{s,t\}\to \infty }\left|{\frac {\sigma ^{2}}{2\theta }}(e^{-\theta |s-t|}-e^{-\theta (s+t)})-{\frac {\sigma ^{2}}{2\theta }}e^{-\theta |s-t|}\right|=0\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348cdff011f68b6548356f502f5d98b3d566f79c)

