Summennorm

Die Summennorm, Betragssummennorm oder 1-Norm ist in der Mathematik eine Vektornorm. Sie ist definiert als die Summe der Beträge der Vektorkomponenten und ist eine spezielle p-Norm für die Wahl von . Die Einheitssphäre der reellen Summennorm ist ein Kreuzpolytop mit minimalem Volumen über alle p-Normen. Daher ergibt die Summennorm für einen gegebenen Vektor den größten Wert aller p-Normen. Die von der Summennorm abgeleitete Metrik ist die Manhattan-Metrik.
Definition[Bearbeiten | Quelltext bearbeiten]
Ist ein n-dimensionaler Vektor mit reellen oder komplexen Einträgen für , dann ist die Summennorm des Vektors definiert als
- .
Die Summennorm entspricht damit der Summe der Beträge der Komponenten des Vektors und wird daher auch etwas genauer Betragssummennorm genannt.[1] Sie ist eine spezielle p-Norm für die Wahl von und heißt deswegen auch 1-Norm.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Reeller Vektor
Die Summennorm des reellen Vektors ist gegeben als
- .
Komplexer Vektor
Die Summennorm des komplexen Vektors ist gegeben als
- .
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Normeigenschaften[Bearbeiten | Quelltext bearbeiten]
Die Summennorm erfüllt wie alle p-Normen die drei Normaxiome, die hier besonders leicht zu zeigen sind. Die Definitheit folgt aus der Eindeutigkeit der Nullstelle der Betragsfunktion durch
- ,
die absolute Homogenität folgt aus der Homogenität der Betragsnorm über
und die Subadditivität folgt direkt aus der Dreiecksungleichung für reelle oder komplexe Zahlen
- .
Einheitssphäre[Bearbeiten | Quelltext bearbeiten]

Die Einheitssphäre der reellen Summennorm, also die Menge
hat in zwei Dimensionen die Form eines Quadrats, in drei Dimensionen die Form eines Oktaeders und in allgemeinen Dimensionen die Form eines Kreuzpolytops. Das Volumen der Einheitskugel der Summennorm ist dabei minimal über alle p-Normen; es beträgt .
Vergleich mit den anderen p-Normen[Bearbeiten | Quelltext bearbeiten]
Die Summennorm ist von allen p-Normen die größte, das heißt für einen gegebenen Vektor und gilt
- ,
wobei Gleichheit genau dann gilt, wenn der Vektor der Nullvektor oder ein Vielfaches eines Einheitsvektors ist. Umgekehrt kann die Summennorm aufgrund der Äquivalenz von Normen in endlichdimensionalen Vektorräumen nach oben gegen jede p-Norm durch
abgeschätzt werden, wobei Gleichheit für einen konstanten Vektor gilt. Die Äquivalenzkonstante bezüglich der Maximumsnorm ist dabei gleich , was maximal zwischen allen p-Normen ist.
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Abgeleitete Begriffe[Bearbeiten | Quelltext bearbeiten]
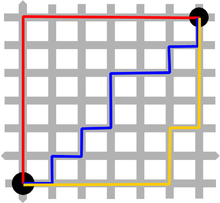
Die Summennorm ist im Gegensatz zur euklidischen Norm (2-Norm) nicht von einem Skalarprodukt induziert. Die von der Summennorm abgeleitete Metrik ist die Manhattan-Metrik oder Taxi-Metrik
- .
Im reellen zweidimensionalen Raum misst sie den Abstand zweier Punkte wie die Fahrtstrecke auf einem gitterförmigen Stadtplan, auf dem man sich nur in senkrechten und waagerechten Abschnitten bewegen kann. Die von der Summennorm induzierte Matrixnorm ist die Spaltensummennorm.
Betrag von Multiindizes[Bearbeiten | Quelltext bearbeiten]
Die Summennorm wird häufig als Betrag eines Multiindex mit nichtnegativen Einträgen verwendet. Beispielsweise kann eine partielle Ableitung einer Funktion mehrerer Veränderlicher als
geschrieben werden, wobei dann die Ordnung der Ableitung ist.
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Die Summennorm kann auch auf unendlichdimensionale Vektorräume über den reellen oder komplexen Zahlen verallgemeinert werden und hat dann eigene Namen.
ℓ1-Norm[Bearbeiten | Quelltext bearbeiten]
Die ℓ1-Norm ist die Verallgemeinerung der Summennorm auf den Folgenraum der betragsweise summierbaren Folgen . Hierbei wird lediglich die endliche Summe durch eine unendliche ersetzt und die ℓ1-Norm ist dann gegeben als
- .
L1-Norm[Bearbeiten | Quelltext bearbeiten]
Weiter kann die Summennorm auf den Funktionenraum der auf einer Menge betragsweise integrierbaren Funktionen verallgemeinert werden, was in zwei Schritten geschieht. Zunächst wird die -Norm einer betragsweise Lebesgue-integrierbaren Funktion als
- ,
definiert, wobei im Vergleich zur ℓ1-Norm lediglich die Summe durch ein Integral ersetzt wurde. Dies ist zunächst nur eine Halbnorm, da nicht nur die Nullfunktion, sondern auch alle Funktionen, die sich nur an einer Menge mit Lebesgue-Maß Null von der Nullfunktion unterscheiden, zu Null integriert werden. Daher betrachtet man die Menge der Äquivalenzklassen von Funktionen , die fast überall gleich sind, und erhält auf diesem L1-Raum die L1-Norm durch
- .
Literatur[Bearbeiten | Quelltext bearbeiten]
- Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2008, ISBN 3-540-34186-2.
- Rolf Walter: Einführung in die Analysis 2. de Gruyter, 2007, ISBN 978-3-11-019540-8.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: L^1-Norm. In: MathWorld (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Rolf Walter: Einführung in die Analysis 2. S. 37.


































![{\displaystyle [f]\in L^{1}(\Omega )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40aa97b4c7d9feff76a51e6aea6a15d4864be66)
![{\displaystyle \|\,[f]\,\|_{L^{1}(\Omega )}=\|f\|_{{\mathcal {L}}^{1}(\Omega )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93b236d2632e646e61af5b61dc0176d904b8fbe)