Quadrat

In der Geometrie ist ein Quadrat (alter Name: Geviert) ein spezielles Polygon, nämlich ein ebenes, konvexes und regelmäßiges Viereck. Es hat vier gleich lange Seiten und vier rechte Winkel. Das Quadrat ist ein Sonderfall des Rechtecks, der Raute, des Parallelogramms, des Trapezes und des Drachenvierecks. Für die Konstruktion eines Quadrats genügt eine Angabe, z. B. der Länge der Seite oder der Diagonalen.
Quadrate sind die Seitenflächen eines platonischen Körpers, nämlich des Würfels. Das Quadrat ist zudem Grundform einer platonischen Parkettierung. Als Spezialfall entsprechender allgemeiner n-dimensionaler Körper ist das Quadrat sowohl der zweidimensionale Hyperwürfel als auch das zweidimensionale Kreuzpolytop.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Für das Quadrat gilt:
- Die vier Seiten sind gleich lang, d. h., es ist eine Raute und ein gleichseitiges Polygon.
- Die vier Innenwinkel sind gleich, d. h., es ist ein Rechteck und ein gleichwinkliges Polygon. Die Innenwinkel sind rechte Winkel.
- Die beiden Diagonalen sind gleich lang, halbieren einander und sind orthogonal.
- Der Schnittpunkt der Diagonalen ist Umkreis- und Inkreismittelpunkt und Symmetriezentrum. Das Quadrat ist sowohl Sehnen- als auch Tangentenviereck.
- Der Flächeninhalt des Umkreises ist doppelt so groß wie der des Inkreises.
- Es hat 4 Symmetrieachsen: die beiden Mittelsenkrechten und die beiden Diagonalen.
- Es ist 4-zählig drehsymmetrisch und daher auch punktsymmetrisch.
- Die Symmetriegruppe ist die Diedergruppe .
Das Quadrat kann charakterisiert werden als:
- Rechteck mit zwei benachbarten gleich langen Seiten
- Raute mit zwei benachbarten gleichen Winkeln
- Raute mit einem rechten Winkel
- Parallelogramm mit zwei benachbarten gleich langen Seiten und zwei benachbarten gleichen Winkeln
- Parallelogramm mit zwei benachbarten gleich langen Seiten und einem rechten Winkel
- Viereck mit gleich langen, orthogonalen Diagonalen, die sich halbieren
Formeln[Bearbeiten | Quelltext bearbeiten]
| Mathematische Formeln zum Quadrat | ||
|---|---|---|
| Flächeninhalt | ||
| Umfang | ||
| Länge der Diagonalen | ||
| Inkreisradius | ||
| Umkreisradius | ||
| Innenwinkel | ||
Konstruktion[Bearbeiten | Quelltext bearbeiten]
Das Quadrat ist ein mit Zirkel und Lineal konstruierbares regelmäßiges Polygon.
Konstruktion mit gegebener Seitenlänge[Bearbeiten | Quelltext bearbeiten]
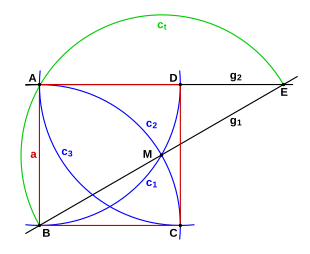
- Gegeben: Die Seite a mit den Endpunkten A und B.
- Ziehe um Ende A einen Kreisbogen (c1, mindestens ein Viertelkreis) mit der Seitenlänge als Radius.
- Ziehe um Ende B einen Kreisbogen (c2, mindestens ein Viertelkreis) mit der Seitenlänge als Radius. Der Schnittpunkt der Kreise ist Punkt M.
- Zeichne eine Gerade durch die Punkte B und M (mindestens doppelt so lang wie BM)
- Zeichne einen Thaleskreis (ct) um M durch B. Man erhält Punkt E.
- Zeichne eine Gerade durch die Punkte A und E. Der Schnittpunkt mit c1 ist Ecke D des späteren Quadrats.
- Ziehe um D der einen Kreisbogen (c3) mit der Seitenlänge als Radius. Der Schnittpunkt mit c2 ist Ecke C.
- Verbinde die Ecken zu einem Quadrat.
Konstruktion mit gegebener Diagonale[Bearbeiten | Quelltext bearbeiten]

- Gegeben: Die Diagonale d mit den Endpunkten A und C.
- Konstruiere auf der Diagonale die Mittelsenkrechte (blau). Der Schnittpunkt mit der Diagonalen ist der Mittelpunkt M.
- Ziehe um M einen Kreis durch A. Die Schnittpunkte mit der Mittelsenkrechten sind die beiden fehlenden Ecken B und D.
- Verbinde die Ecken A, B, C, und D zyklisch miteinander.
Animationen[Bearbeiten | Quelltext bearbeiten]
Ineinander liegende Quadrate[Bearbeiten | Quelltext bearbeiten]

Der kanadische Mathematiker Ross Honsberger verglich in einer seiner Schriften unter anderem die Flächenmaßzahlen zweier ineinander liegender Quadrate und entdeckte folgenden Zusammenhang:
- Verbindet man die vier Eckpunkte eines Quadrats geradlinig mit den Mittelpunkten der gegenüber liegenden Seiten, so entsteht ein zweites inneres Quadrat, dessen Flächenmaßzahl ein Fünftel der Flächenmaßzahl des Ausgangsquadrats beträgt.[1][2]
Diese Aussage lässt sich geometrisch durch Umordnung von Teilflächen veranschaulichen.
Die dunkelblauen kongruenten rechtwinkligen Dreiecke werden dem Ausgangsquadrat (linke Figur) entnommen und ergänzen die hellblauen Trapeze zu Quadraten (rechte Figur). Somit ist die linke Figur flächengleich zu der aus fünf kongruenten Quadraten bestehenden rechten kreuzförmigen Figur.
Der Anteil des roten Quadrats an der Gesamtfigur beträgt demnach ein Fünftel.
Zwei sich berührende Quadrate[Bearbeiten | Quelltext bearbeiten]




Im Folgenden seien jeweils zwei Quadrate gegeben, die sich an einer Ecke berühren, und durch je zwei (grün und gelb gefärbte) sogenannte Flankendreiecke ergänzt werden. Aus der besonderen Lage der beiden Quadrate zueinander lassen sich Eigenschaften der Flankendreiecke bezüglich ihrer Flächenmaßzahlen und ihrer Transversalen herleiten.
Flächengleichheit von Flankendreiecken[Bearbeiten | Quelltext bearbeiten]
Eigenschaft 1:
- Die beiden Flankendreiecke zweier sich an einer Ecke berührender Quadrate sind flächengleich.
Algebraischer Beweis:
- Wegen gilt . Durch Multiplikation mit auf beiden Seiten der Gleichung folgt weiter
- .
- Deshalb sind nach der Flächeninhaltsformel für allgemeine Dreiecke die beiden Flankendreiecke flächengleich.
Geometrischer Beweis:
- Dreht man im Uhrzeigersinn das obere grüne Dreieck um 90° um den gemeinsamen Eckpunkt der beiden Quadrate, so erkennt man, dass das grüne und das gelbe Dreieck in der Länge einer Seite und der darauf errichteten Höhe übereinstimmen, woraus unmittelbar die behauptete Flächengleichheit folgt (Figur 1 und 2).
Transversalen in Flankendreiecken[Bearbeiten | Quelltext bearbeiten]
Eigenschaft 2:
- Die Höhe eines der beiden Flankendreiecke und die Seitenhalbierende des anderen Flankendreiecks zweier sich an einer Ecke berührender Quadrate liegen auf einer gemeinsamen Transversalen beider Dreiecke.
Geometrischer Beweis:
- Dreht man das obere grüne Dreieck zunächst um 90° im Uhrzeigersinn und anschließend um 90° gegen den Uhrzeigersinn um den gemeinsamen Eckpunkt der beiden Quadrate, so liegen die gedrehten roten Strecken parallel zur Grundseite des gelben Dreiecks. Die äußeren Seiten der gedrehten Flankendreiecke sind ebenfalls parallel zueinander. Damit gilt . Hieraus folgt, dass die zur Grundseite des gelben Dreiecks gedrehten roten Strecken Seitenhalbierenden der grünen Dreiecke sind. Nach dem Zurückdrehen in die ursprüngliche Position liegen somit die roten Strecken auf einer gemeinsamen Transversalen beider Dreiecke (Figur 3 und 4).[3]
Quadrate in der erweiterten Vecten-Figur[Bearbeiten | Quelltext bearbeiten]

Erweitert man die Vecten-Figur um drei weitere Quadrate wie in Figur 5, so ist die Flächeninhaltssumme der drei äußeren Quadrate dreimal so groß wie die der drei inneren Quadrate:
Beweis:
- Bezüglich der Lage der Seiten und Winkel im mittleren Dreieck der Figur 5 werden die Standardbezeichnungen , und sowie , und in der üblichen Reihenfolge gegen den Uhrzeigersinn verwendet. Nach dem Kosinussatz und der Symmetrieeigenschaft
- gelten die Beziehungen
- und
- .
- Hieraus folgt:
- (1)
- Analog erhält man:
- (2)
- (3)
- Aus (1), (2) und (3) folgt unmittelbar:
- was zu zeigen war.[4]
Quadrate im Kreis und im Halbkreis[Bearbeiten | Quelltext bearbeiten]
Einem Kreis sei ein Quadrat und einem Halbkreis mit demselben Radius ein weiteres Quadrat einbeschrieben. Dann hat das größere Quadrat den -fachen Flächeninhalt des kleineren Quadrats.
Die Beweisfiguren werden wie abgebildet in eine Parkettierung aus Einheitsquadraten eingebettet. Hierbei wurden die Seiten des größeren Quadrats so gedreht, dass der Satz des Pythagoras anwendbar ist. Das kleinere Quadrat hat den Flächeninhalt . Nach dem Satz des Pythagoras beträgt die Seitenlänge des größeren Quadrats . Demnach hat es den Flächeninhalt und ist somit -mal so groß wie das kleinere Quadrat.[5]
Quadrate am Sinusgraphen[Bearbeiten | Quelltext bearbeiten]

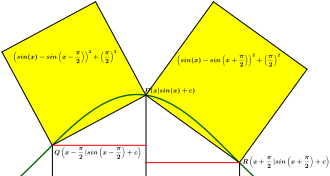
Die Invarianz von Quadratsummen gilt für die Kathetenquadrate beim Satz des Pythagoras. In gewisser Analogie hierzu treten unter bestimmten Voraussetzungen invariante Quadratsummen auch im Zusammenhang mit der Sinusfunktion auf.[6][7]
Gegeben sei der ganz oberhalb der x-Achse verlaufende Graph einer Sinusfunktion mit der Gleichung für und ein beliebiger Punkt des Graphen, sowie ein Punkt links von und ein Punkt rechts von , wobei die x-Koordinaten von und eine halbe Periodenlänge, also , voneinander entfernt sind.
Dann hat die Gesamt-Flächenmaßzahl der beiden Quadrate über und unabhängig von der Lage des Punktes stets denselben Wert, nämlich .
In der abgebildeten Beispielfigur sind obige Voraussetzungen erfüllt. Die fünf verschieden gefärbten Quadratpaare haben dieselbe Flächenmaßzahl.
Der Beweis verwendet den Satz des Pythagoras und die Additionstheoreme der Trigonometrie. Die Punkte , , haben folgende Koordinaten:
- , ,
Dann beträgt die Gesamt-Flächenmaßzahl der beiden Quadrate nach zweimaliger Anwendung des Pythagoras-Satzes und elementaren Termumformungen unter Verwendung der Additionstheoreme:
Parkettierungen mit Quadraten[Bearbeiten | Quelltext bearbeiten]
Einige platonische und archimedische Parkettierungen enthalten Quadrate. Diese Parkettierungen sind periodisch, drehsymmetrisch und translationssymmetrisch und enthalten ausschließlich regelmäßige Polygone.
-
3-3-3-4-4
-
3-3-4-3-4
-
3-4-6-4
-
4-8-8
-
4-6-12
Die Zahlen unter den Abbildungen geben an, wie viele Ecken die regelmäßigen Polygone haben, die jeweils an einem Punkt zusammenstoßen. Die Innenwinkel ergeben zusammen 360°.
Polyeder mit Quadraten[Bearbeiten | Quelltext bearbeiten]
Der Würfel ist der einzige platonischen Körper, der quadratische Seitenflächen hat. Auch einige archimedische Körper enthalten Quadrate, zum Beispiel das Kuboktaeder, der Oktaederstumpf, das Rhombenkuboktaeder und das Rhombenikosidodekaeder.
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
In der euklidischen Geometrie ist das Quadrat der zweidimensionale Spezialfall von Hyperwürfel und Kreuzpolytop.
Der Begriff Quadrat wird in der synthetischen Geometrie der affinen Ebene verallgemeinert, indem eine der äquivalenten Aussagen, die ein Quadrat in der elementaren Geometrie beschreiben, zur Definition des Begriffes verwendet wird. Zum Beispiel wird für präeuklidische Ebenen die Existenz dieser Figuren zu einem zusätzlichen Axiom.
In nichteuklidische Geometrien sind Quadrate allgemein Polygone mit 4 gleich langen Seiten und gleichen Innenwinkeln.
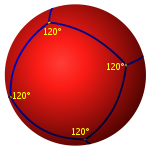
In der sphärischen Geometrie ist ein Quadrat ein Polygon, dessen Seiten Großkreise sind, die sich im gleichen Winkel schneiden. Anders als bei Quadraten der ebenen Geometrie sind die Winkel eines sphärischen Quadrats größer als ein rechter Winkel. Größere sphärische Quadrate haben größere Winkel.
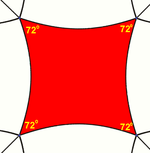
In der hyperbolischen Geometrie existieren keine Quadrate mit rechten Winkeln. Stattdessen haben Quadrate Winkel, die kleiner als ein rechter Winkel sind. Größere hyperbolische Quadrate haben kleinere Winkel.
| Verallgemeinerungen des Quadrats | ||||
|---|---|---|---|---|
| Geometrie | sphärische Geometrie | sphärische Geometrie | euklidische Geometrie | hyperbolische Geometrie |
| Innenwinkel | 180° | 120° | 90° | 72° |
| Schläfli-Symbol | {4, 2} | {4, 3} | {4, 4} | {4, 5} |
| Anzahl der Quadrate in der Parkettierung | 2 | 6 | unendlich | unendlich |
|
|

|
| |
Lateinisches Quadrat[Bearbeiten | Quelltext bearbeiten]
Ein lateinisches Quadrat ist ein quadratisches Schema mit n Reihen und Spalten, wobei jedes Feld mit einem von n verschiedenen Symbolen belegt ist, so dass jedes Symbol in jeder Zeile und in jeder Spalte jeweils genau einmal auftritt. Die natürliche Zahl n wird Ordnung des lateinischen Quadrats genannt.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Magisches Quadrat[Bearbeiten | Quelltext bearbeiten]

Ein magisches Quadrat der Kantenlänge n ist eine quadratische Anordnung der natürlichen Zahlen 1, 2, …, n², bei der die Summen der Zahlen aller Zeilen, Spalten und der beiden Diagonalen gleich sind. Diese Summe wird als die magische Zahl des magischen Quadrates bezeichnet.
Quadratur des Quadrates[Bearbeiten | Quelltext bearbeiten]

Die Quadratur des Quadrates ist die Parkettierung eines gegebenen Quadrates mit kleineren Quadraten, deren Seitenlängen ganzzahlige Werte haben. Interessant und anspruchsvoll wird die Aufgabenstellung durch folgende Zusatzbedingungen:
- Keine zwei Teilquadrate sollen die gleiche Größe haben. Eine Quadrat-Parkettierung, die diese Bedingung erfüllt, heißt perfekt.
- Wenn eine Teilmenge der Teilquadrate ein Rechteck bildet, heißt die Quadratur zusammengesetzt, andernfalls einfach.
Quadratur des Kreises[Bearbeiten | Quelltext bearbeiten]

Die Quadratur des Kreises ist ein klassisches Problem der Geometrie. Die Aufgabe besteht darin, aus einem gegebenen Kreis in endlich vielen Schritten ein Quadrat mit dem gleichen Flächeninhalt zu konstruieren. Sie ist äquivalent zur sogenannten Rektifikation des Kreises, also der Konstruktion einer geraden Strecke, die dem Kreisumfang entspricht. Das wiederum entspricht der Konstruktion der Kreiszahl aus der Strecke 1. Beschränkt man die Konstruktionsmittel auf Lineal und Zirkel, so ist die Aufgabe aufgrund der Transzendenz von unlösbar. Dies konnte 1882 von dem deutschen Mathematiker Ferdinand von Lindemann bewiesen werden.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Quadratur des Rechtecks
- Quadratur des Polygons
- Animierte Lernsequenz (Konstruktion, Umfang, Flächeninhalt)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 157
- ↑ Ross Honsberger: Mathematical Morsels Mathematical Association of America, Washington 1978, S. 204–205
- ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie - Eine etwas andere Einführung in die Euklidische Geometrie. Zweite korrigierte und ergänzte Auflage, Springer Spektrum, Springer-Verlag GmbH, Berlin 2021, ISBN 978-3-662-63830-9, S. 85–90
- ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie - Eine etwas andere Einführung in die Euklidische Geometrie. Zweite korrigierte und ergänzte Auflage, Springer Spektrum, Springer-Verlag GmbH, Berlin 2021, ISBN 978-3-662-63830-9, S. 94/95
- ↑ Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik - 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen, Springer Spektrum, Springer-Verlag GmbH Berlin 2015, ISBN 978-3-662-45460-2, Seiten 257, 258, 304
- ↑ Hans Walser: Spiel mit Quadraten In: MU, Der Mathematikunterricht, Jahrgang 67, Heft 3-2021, S. 17-27, ISSN 0025-5807
- ↑ Invariante Flächensumme auf der Sinuskurve PDF-Skript zum Vortrag von Hans Walser, Buchautor und Lehrbeauftragter für Mathematik an mehreren Schweizer Hochschulen, auf dem 24. Forum für Begabungsförderung in Mathematik 2023, Wolfratshausen, abgerufen am 13. August 2023