Windschiefe


In der Geometrie nennt man zwei Geraden windschief, wenn sie sich weder schneiden noch parallel zueinander sind.[1] Dies ist im zweidimensionalen Raum nicht möglich, da hier alle denkbaren Geraden in der gleichen Ebene liegen und sich schneiden oder parallel sind. Windschiefe Geraden gibt es daher nur in mindestens dreidimensionalen Räumen.
Das Wort „windschief“ stammt von der Vorstellung, dass zwei ursprünglich parallele Geraden um ihre Verbindungsachse (Transversale) „gewunden“, also verdreht wurden.[2]
Zum Nachweis, dass zwei Geraden und windschief sind, genügt es zu zeigen, dass ein Richtungsvektor von , ein Richtungsvektor von und ein Verschiebungsvektor von einem Punkt auf zu einem Punkt auf linear unabhängig sind. Äquivalent kann man zeigen, dass es keine Ebene gibt, die beide Geraden enthält.
Berechnung des Abstandes zweier windschiefer Geraden[Bearbeiten | Quelltext bearbeiten]
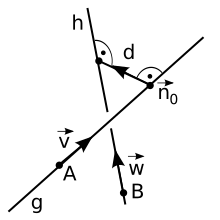
Die eindeutig bestimmte Strecke kleinster Länge, die zwei windschiefe Geraden und verbindet, nennt man Gemeinlot der beiden Geraden. Die Gerade, auf der das Gemeinlot liegt, nennt man die Minimaltransversale der beiden Geraden. Diese ist diejenige eindeutig bestimmte Gerade, welche im rechten Winkel zu den beiden Geraden steht. Die Länge des Gemeinlots von und ist der Abstand der beiden Geraden.
Gegeben seien die windschiefen Geraden und mit den Stützpunkten und bzw. den Stützvektoren und den Richtungsvektoren und . Dann sind die Parameterformen der Geradengleichungen
- ,
wobei gilt und die drei Vektoren linear unabhängig sein müssen.
Der Normalenvektor , der senkrecht auf den beiden Richtungsvektoren und steht, lässt sich über das Kreuzprodukt berechnen:
- und auf die Länge 1 bringen: .
Die Berechnung des Abstandes ist möglich durch die orthogonale Projektion des Verbindungsvektors der Stützpunkte auf den Normalenvektor. Dazu wird der Normalenvektor auf die Länge 1 gebracht. Der Abstand der beiden windschiefen Geraden beträgt dann
- .
Schreibweise mit Determinanten[Bearbeiten | Quelltext bearbeiten]
Die beiden Geradengleichungen lauten ausgeschrieben
- .
Der Abstand der beiden windschiefen Geraden mit Hilfe der Determinante det beträgt dann
- .
Bestimmung der Lotfußpunkte[Bearbeiten | Quelltext bearbeiten]

Den Lotfußpunkt erhält man, indem man eine Hilfsebene aufstellt. Der Punkt liegt auf der Hilfsebene, und spannen die Hilfsebene auf.
- ,
wobei der Normalenvektor bestimmt wird durch
- .
Der Schnittpunkt von und ergibt den Lotfußpunkt :
- mit
Analog erhält man mit der Ebene und ihrem Schnittpunkt mit :
- mit
Bei dieser Methode muss der Abstand nicht berechnet werden.
Die Lotfußpunkte können auch so bestimmt werden, dass man die beiden (vorerst unbekannten) Punkte ansetzt:
- und
und dann einen entlang verschiebt und ihn mit dem anderen zur Deckung bringt:
- .
Eine zeilenweise Auflösung ergibt ein System mit drei Variablen: , und . Die Fußpunkte sind dann:
- und .
Der Abstand ergibt sich aus
Bemerkung[Bearbeiten | Quelltext bearbeiten]
- Im Taschenbuch der Mathematik von I.N. Bronstein und K.A. Semendjajew wird „kreuzend“ als Synonym für „windschief“ genannt.[3]
Literatur[Bearbeiten | Quelltext bearbeiten]
- M. Jeger, B. Eckmann: Einführung in die vektorielle Geometrie und lineare Algebra für Ingenieure und Naturwissenschafter. Birkhäuser Verlag, Basel / Stuttgart 1967.
- Joachim Köhler et al.: Analytische Geometrie und Abbildungsgeometrie in vektorieller Darstellung. Diesterweg-Verlag, Frankfurt am Main 1971, ISBN 3-425-05302-7
- Joachim Köhler et al.: Analytische Geometrie und Abbildungsgeometrie in vektorieller Darstellung. Diesterweg-Verlag, Frankfurt am Main 1971, ISBN 3-425-05302-7
- Wilmut Kohlmann et al.: Lineare Algebra und Analytische Geometrie. Vieweg-Verlag, Braunschweig 1977, ISBN 3-594-10826-0
- Elisabeth und Friedrich Barth, Gert Krumbacher: Anschauliche Analytische Geometrie. Oldenbourg-Verlag, München 1997, ISBN 3-486-03500-2
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Meyers Rechenduden. Bibliographisches Institut, Mannheim 1960, S. 807
- ↑ DWDS – Digitales Wörterbuch der deutschen Sprache. Abgerufen am 20. Mai 2021.
- ↑ Abschnitt 3.3.1.1 Zwei Geraden in der Google-Bücher-Suche für das Taschenbuch der Mathematik
















![{\displaystyle g\colon {\vec {x}}=\left({\begin{smallmatrix}a_{1}\\[0.7ex]a_{2}\\[0.7ex]a_{3}\end{smallmatrix}}\right)+r\left({\begin{smallmatrix}v_{1}\\[0.7ex]v_{2}\\[0.7ex]v_{3}\end{smallmatrix}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3160bfc87366a2eac81e4665f233f44189958a4)
![{\displaystyle h\colon {\vec {x}}=\left({\begin{smallmatrix}b_{1}\\[0.7ex]b_{2}\\[0.7ex]b_{3}\end{smallmatrix}}\right)+s\left({\begin{smallmatrix}w_{1}\\[0.7ex]w_{2}\\[0.7ex]w_{3}\end{smallmatrix}}\right)\ \ \,r,s\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e993c87603d44aa990413dee0130fdc4c25de39e)



















