Ähnlichkeit (Geometrie)

In der Geometrie sind zwei Figuren genau dann zueinander ähnlich, wenn sie durch eine Ähnlichkeitsabbildung (auch diese Abbildung wird häufig als Ähnlichkeit bezeichnet) ineinander überführt werden können. Das heißt, es gibt eine geometrische Abbildung, die sich aus zentrischen Streckungen und Kongruenzabbildungen (also Verschiebungen, Drehungen, Spiegelungen) zusammensetzen lässt und die eine Figur auf die andere abbildet. Ähnlichkeit erweitert somit die Kongruenz (Deckungsgleichheit) von Figuren um die Möglichkeit der Streckung.
In der Tabelle sind die ersten drei Kongruenz-Abbildungen. Man beachte, dass eine Spiegelung Orientierungen umkehrt. Nur zentrische Streckungen ändern Längen.
 |
 |
 |
 |
Eigenschaften[Bearbeiten | Quelltext bearbeiten]

Winkel und Streckenverhältnisse stimmen in ähnlichen Figuren überein; somit sind alle Kreise sowie jeweils alle regelmäßigen Vielecke gleicher Eckenzahl, wie gleichseitige Dreiecke oder Quadrate, zueinander ähnlich.
Es gilt, dass kongruente Figuren stets ähnlich sind. Das Umgekehrte ist hingegen falsch: Ähnliche Figuren sind nicht notwendigerweise kongruent, da sie verschieden groß sein können.
Als mathematisches Zeichen für geometrische Ähnlichkeit wird (die Tilde) verwendet, z.B: bedeutet, dass die Dreiecke und ähnlich sind. Will man dagegen Kongruenz ausdrücken, so kann stattdessen oder (eine „Mischung“ mit dem Gleichheitszeichen) verwendet werden.
Ähnlichkeit bei Dreiecken[Bearbeiten | Quelltext bearbeiten]
Dreiecke spielen hier eine zentrale Rolle, da sich sehr viele Figuren auf solche zurückführen lassen. Es gilt:
Zwei Dreiecke sind zueinander ähnlich, wenn
- sie in zwei (und somit in allen drei) Winkeln übereinstimmen; oder
- sie in allen Verhältnissen entsprechender Seiten übereinstimmen; oder
- sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen; oder
- sie im Verhältnis zweier Seiten und im Gegenwinkel der größeren Seite übereinstimmen.
Diese Sätze werden Ähnlichkeitssätze genannt.

Strahlensätze[Bearbeiten | Quelltext bearbeiten]
Die Strahlensätze machen über die Verhältnisse der Dreiecksseiten bestimmter ähnlicher Dreiecke wichtige Aussagen.
Ähnliche Kegelschnitte[Bearbeiten | Quelltext bearbeiten]
- Zwei nicht ausgeartete Kegelschnitte (Ellipse, Hyperbel, Parabel) sind ähnlich, wenn sie dieselbe Exzentrizität besitzen.
Die Ähnlichkeit aller Parabeln (ihre Exzentrizität ist 1) wird in dem Artikel Parabeln gezeigt.
Eine Ellipse/Hyperbel mit Halbachsen besitzt die Exzentrizität Eine Streckung um den Faktor am Mittelpunkt ändert die Exzentrizität nicht.
Selbstähnlichkeit logarithmischer Spiralen[Bearbeiten | Quelltext bearbeiten]

Die logarithmische Spirale kann man einerseits als Bild der Spirale unter der Streckung am Nullpunkt mit dem Faktor , aber auch als Bild von unter der Rotation um den Winkel auffassen.
Eine Kurve, deren Bilder unter zentrischen Streckungen zu ihr selbst kongruent sind, nennt man selbstähnlich. Also:
- Die Spirale ist selbstähnlich.
Im Bild: Die Spiralen für können auch durch Drehung der roten Spirale um erhalten werden.
Zusammengesetzte ähnliche Figuren (Reptiles)[Bearbeiten | Quelltext bearbeiten]
Definitionen[Bearbeiten | Quelltext bearbeiten]
Ähnliche Figuren, die sich lückenlos zu einer größeren Figur, die zu den kleineren Figuren ähnlich ist, zusammensetzen lassen, werden im Englischen als Reptiles (Abkürzung für replicating tiles) bezeichnet.
Ist die Anzahl der ähnlichen Teilfiguren, so wird die zusammengesetzte Figur rep--Figur genannt.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Im Folgenden sei .
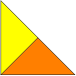
- Jedes Dreieck ist eine rep--Figur (Figuren 1 und 2).
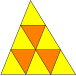
- Jedes gleichschenklig-rechtwinklige Dreieck ist zusätzlich eine rep--Figur (Figur 3).
- Jedes Dreieck mit den Innenwinkeln 30°, 60° und 90° ist zusätzlich eine rep--Figur (Figur 4).
- Jedes rechtwinklige Dreieck, bei dem eine Kathete die doppelte Länge der anderen hat, ist zusätzlich eine rep--Figur (Figur 5).
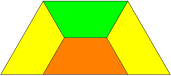
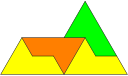
- Unter den gleichschenkligen Trapezen gibt es rep--Figuren und rep--Figuren (Figuren 6 und 7).
- Es gibt besondere konkave Fünfecke, die an die Form der Sphinx erinnern und deshalb in der englischsprachigen Wikipedia unter Sphinx tiling zu finden sind. Unter diesen Fünfecken gibt es ebenfalls rep--Figuren und rep--Figuren (Figuren 8 und 9).
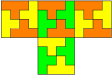
- Unter den verschiedenen Arten von Polyominos gibt es rep--Figuren und rep--Figuren (Figuren 10, 11 und 12).[1][2]
-
Figur 1
-
Figur 2
-
Figur 3
-
Figur 4
-
Figur 5
-
Figur 6
-
Figur 7
-
Figur 8
-
Figur 9
-
Figur 10
-
Figur 11
-
Figur 12
Ähnlichkeit in der fraktalen Geometrie[Bearbeiten | Quelltext bearbeiten]

Skaleninvariante Ähnlichkeit in gebrochenen, „fraktalen“ Dimensionen ist Gegenstand der fraktalen Geometrie.
Die Ähnlichkeit ist dabei das Ergebnis der Rekursion nichtlinearer Algorithmen. Ein bekanntes Beispiel ist die Mandelbrot-Menge, deren Grenzlinie an jeder Stelle Ähnlichkeit mit den angrenzenden Abschnitten in allen Größenordnungen aufweist.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik - 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen, Springer Spektrum, Springer-Verlag GmbH Berlin Heidelberg 2015, ISBN 978-3-662-45460-2, Seiten 51 bis 54
- ↑ George E. Martin: Polyominoes: A Guide to Puzzles and Problems in Tiling, AMS/MAA, Washington 1991