Höhe (Geometrie)

Die Höhen und verlaufen außerhalb des Dreiecks, da sich bei B ein stumpfer Winkel befindet. Verlängert man diese Höhen jeweils über die zugehörigen Lotfußpunkte La und Lc sowie die Höhe über den Eckpunkt B hinaus, so schneiden sich alle drei Geraden im Höhenschnittpunkt H.
Unter einer Höhe versteht man in der Geometrie ein besonderes Lot (Senkrechte) auf eine Strecke oder eine Fläche sowie dessen Länge. Höhen spielen bei der Berechnung von Flächen- und Rauminhalten (Volumina) eine wichtige Rolle. Sie können auch außerhalb von Figuren und Körpern liegen, z. B. bei stumpfwinkligen Dreiecken.
Höhen bei Dreiecken[Bearbeiten | Quelltext bearbeiten]
Fällt man das Lot von einer Ecke auf die gegenüberliegende Dreiecksseite, so schneidet es diese Seite im Lotfußpunkt. Die Strecke zwischen Ecke und Lotfußpunkt nennt man Höhe und das von den drei Lotfußpunkten gebildete Dreieck wird auch als Höhenfußpunktdreieck bezeichnet. Jedes Dreieck besitzt genau drei Höhen. Diese schneiden sich in einem gemeinsamen Punkt, dem Höhenschnittpunkt. Er liegt für spitzwinklige Dreiecke innerhalb und für stumpfwinklige Dreiecke außerhalb des Dreiecks. Beim rechtwinkligen Dreieck fällt er mit der rechtwinkligen Ecke zusammen. Die Höhen eines Dreieck sind zudem die Winkelhalbierenden seines Höhenfußpunktdreiecks. Für die Höhen , und in einem Dreieck mit Seiten , und bezeichnen im Folgenden die Radien des In- und Umkreises und die Innenwinkel in den Eckpunkten . Zwischen den Seiten und Höhen des Dreieck besteht die folgende Beziehung:
Über diese Verhältnisgleichung hinaus gilt genauer:
Hieraus erhält man die folgende Darstellung des Produktes der drei Höhen:
Zum Radius des Inkreis besteht die Beziehung:
Bei rechtwinkligen Dreiecken spielt der Höhensatz des Euklid eine große Rolle.
 |
 |
Höhe von Trapez und Parallelogramm[Bearbeiten | Quelltext bearbeiten]
- Ein Trapez besitzt zwei gegenüberliegende Seiten, die parallel zueinander sind. Den Abstand dieser beiden Parallelen nennt man Höhe des Trapezes.
- Die Höhe eines Parallelogramms ist der senkrechte Abstand der jeweils gegenüberliegenden Seiten.
Höhen weiterer geometrischer Objekte[Bearbeiten | Quelltext bearbeiten]
- Bei Prismen und Zylindern ist die Höhe der senkrechte Abstand von Grund- und Deckfläche.
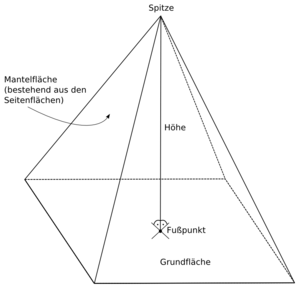
- Bei Pyramiden und Kegeln ist die Höhe der lotrechte Abstand der Spitze von der Grundfläche.
- Auch in höherdimensionalen geometrischen Objekten, wie zum Beispiel der Hyperpyramide, bezeichnet man den (senkrechten) Abstand eines Eckpunktes im n-dimensionalen Raum von einer in einer Hyperebene liegenden Hyperfläche als Höhe.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Schülerduden: Mathematik I, Dudenverlag, 8. Auflage, Mannheim 2008, S. 192–193
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Altitude. In: MathWorld (englisch).
- Höhen im Dreieck auf mathematische-basteleien.de
- All About Altitudes auf cut-the-knot.org