Kaleidozyklus


Ein Kaleidozyklus (von καλός kalós schön, εἶδος eidos Form, Gestalt, κύκλος kyklos Ring, Kreis) ist ein Ring aus einer geraden Anzahl von dreiseitigen Pyramiden (Dreieckspyramiden), die an jeweils zwei gegenüberliegenden windschiefen und senkrecht zueinander verlaufenden Kanten miteinander verbunden sind.
Den Namen prägten die US-amerikanische Professorin für Mathematik am Moravian College in Bethlehem (Pennsylvania), Doris Schattschneider, und der freie Künstler Wallace Walker, die sich mit den Eigenschaften und der Konstruktion solcher Ringe beschäftigten und sie mit Motiven von M. C. Escher dekorierten.
Die Anzahl verschiedener Kaleidozyklen ist unendlich. Sie alle lassen sich fortlaufend in sich so drehen, dass jede Pyramide von allen Seiten sichtbar wird.
Kaleidozyklen aus sechs und acht Dreieckspyramiden
[Bearbeiten | Quelltext bearbeiten]

Bei einem Kaleidozyklus aus sechs Dreieckspyramiden sind diese nicht regelmäßig. In diesem Fall schließt sich der Ring beim Drehen.
Besteht ein Kaleidozyklus aus acht Dreieckspyramiden und handelt es sich bei diesen um regelmäßige Tetraeder, so schließt sich der Ring beim Drehen nicht, sondern lässt in der Mitte eine Lücke. Soll sich der Ring beim Drehen in der Mitte schließen, so muss auf die Regelmäßigkeit der acht Dreieckspyramiden verzichtet werden. Deren Seitenflächen sind dann gleichschenklige statt gleichseitige Dreiecke.[1][2]
Kaleidozyklus als Teil eines Würfels
[Bearbeiten | Quelltext bearbeiten]Ein spezieller Kaleidozyklus aus sechs Dreieckspyramiden besteht aus dem mittleren der drei volumengleichen Teile des umstülpbaren Würfels von Paul Schatz. Während die beiden kongruenten Riegelkörper starr sind, ist der Würfelgürtel ein in sich beweglicher Kaleidozyklus (Abbildungen 1 bis 3).
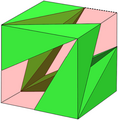
Die auf der Würfeloberfläche liegenden kongruenten Dreiecke sind Begrenzungsflächen der Dreieckspyramiden. Diese Begrenzungsflächen bestehen aus denjenigen rechtwinkligen Dreiecken, die durch Teilung gleichseitiger Dreiecke entlang ihrer Symmetrieachsen entstehen. In der Aufteilung der Würfeloberfläche sind diese Dreiecke sichtbar (Abbildung 4).
Das Netz des Kaleidozyklus-Würfelgürtels besteht aus 12 dieser rechtwinkligen Dreiecke (sechs kongruent und sechs gegensinnig kongruent) sowie sechs Rechtecken (Abbildung 5).[3]
-
Abb. 1: Erster Würfelriegel nach Paul Schatz
-
Abb. 2: Würfelgürtel nach Paul Schatz als Kaleidozyklus
-
Abb. 3: Zweiter Würfelriegel nach Paul Schatz
-
Abb. 4: Dreiecksaufteilung auf der Würfeloberfläche
-
Abb. 5: Netz des Kaleidozyklus-Würfelgürtels
Literatur
[Bearbeiten | Quelltext bearbeiten]- Doris Schattschneider, Wallace G. Walker: M.C. Escher Kaleidozyklen, Taschen Verlag Köln 2019, ISBN 3-822-89600-4 / ISBN 978-3-8228-9600-6
- Peter Berger: Aspekte der Körpergeometrie, PH Ludwigsburg (2016)
- Frankie Jones: Kaleidocycles Paper Shapers, Templar Publishing (2019), ISBN 1-787-41276-8 / ISBN 978-1-7874-1276-7
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Kaleidozyklen falten EDUTHEK des österreichischen Bundesministeriums für Bildung, Wissenschaft und Forschung, abgerufen am 15. Januar 2022
- Mehr Ordnung im „Unendlichkeitszoo“ aus science.orf.at vom 24. Juli 2023, abgerufen am 26. Juli 2023
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Kaleidozyklus Mathematik alpha, abgerufen am 15. Januar 2022
- ↑ Kaleidozyklen Mathematische Basteleien, abgerufen am 15. Januar 2022
- ↑ Die Netze von Kaleidozyklen Website von Prof. Dr. Peter Berger (PH Ludwigsburg) über Aspekte der figurativen Mathematik, abgerufen am 15. Januar 2022