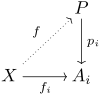In vielen Gebieten der Mathematik spielen direkte Produkte und Koprodukte der betrachteten Objekte eine besondere Rolle. Die Konstruktion solcher Produkte von Objektfamilien fußt oft auf dem kartesischen Produkt von Mengen.
In der Mengenlehre wird das kartesische Produkt einer Familie von Mengen  folgendermaßen definiert:
folgendermaßen definiert:

Sind die  alles Rechtsmoduln über dem unitären Ring
alles Rechtsmoduln über dem unitären Ring  , so hat
, so hat  eine Modulstruktur. Dies ist ein Produkt von Moduln, das Produkt der Modulfamilie
eine Modulstruktur. Dies ist ein Produkt von Moduln, das Produkt der Modulfamilie  .
.
Ist  eine Familie von Rechtsmoduln über dem Ring
eine Familie von Rechtsmoduln über dem Ring  so heißt
so heißt  das Produkt der Moduln. Ist
das Produkt der Moduln. Ist  , so heißt
, so heißt  die
die  -te Komponente von
-te Komponente von  . Das Produkt
. Das Produkt  erhält durch die folgenden beiden Verknüpfungen eine Modulstruktur.
erhält durch die folgenden beiden Verknüpfungen eine Modulstruktur.

Ist die Funktion  , so schreibt man dafür oft
, so schreibt man dafür oft  , analog wie das bei reellen Zahlenfolgen üblich ist[1]. Dabei ist
, analog wie das bei reellen Zahlenfolgen üblich ist[1]. Dabei ist  die
die  -te Komponente. Man addiert also komponentenweise und mit den Skalaren wird komponentenweise multipliziert.
-te Komponente. Man addiert also komponentenweise und mit den Skalaren wird komponentenweise multipliziert.
Ist  das Produkt der Moduln
das Produkt der Moduln  so bilden die Funktionen
so bilden die Funktionen  das Produkt
das Produkt  epimorph auf
epimorph auf  ab. Sie heißen Projektionen.
Das Paar
ab. Sie heißen Projektionen.
Das Paar  hat die folgende Eigenschaft:
hat die folgende Eigenschaft:
Zu jedem Rechtsmodul  über
über  und jeder Familie von Homomorphismen
und jeder Familie von Homomorphismen  gibt es genau einen Homomorphismus
gibt es genau einen Homomorphismus  , so dass
, so dass  für alle
für alle  gilt.
gilt.
In der Kategorientheorie nennt man eine solche Eigenschaft universell, sie kennzeichnet das Produkt von Objekten bis auf Isomorphie, das heißt:
Ist  ein Modul und
ein Modul und  eine Familie von Homomorphismen und gibt es zu jedem Modul
eine Familie von Homomorphismen und gibt es zu jedem Modul  und jeder Familie
und jeder Familie  von Homomorphismen genau ein
von Homomorphismen genau ein  mit
mit  , so ist
, so ist  . Ein Diagramm zu dieser Situation sieht so aus:
. Ein Diagramm zu dieser Situation sieht so aus:
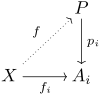
Die oben angegebene Konstruktion zusammen mit dem Nachweis der universellen Eigenschaft fasst man auch kurz so zusammen: In der Kategorie der Moduln gibt es Produkte.
Ist  eine Familie von Homomorphismen, so ist
eine Familie von Homomorphismen, so ist
 genau dann ein Produkt der Familie
genau dann ein Produkt der Familie  , wenn der
Homomorphismus
, wenn der
Homomorphismus

für alle Rechtsmoduln  ein Isomorphismus ist. Insbesondere ist:
ein Isomorphismus ist. Insbesondere ist:

eine natürliche Transformation, die für jeden Modul  ein Isomorphismus ist.
ein Isomorphismus ist.  ist ein funktorieller Isomorphismus.
ist ein funktorieller Isomorphismus.
- Ist für alle
 , so schreibt man
, so schreibt man  und nennt dies eine Potenz von
und nennt dies eine Potenz von  .
.
- Für jede Indexmenge
 ist
ist  sogar ein Ring, wenn man komponentenweise multipliziert.
sogar ein Ring, wenn man komponentenweise multipliziert.  ist auf der linken und rechten Seite ein Modul über dem Ring
ist auf der linken und rechten Seite ein Modul über dem Ring  . Die Diagonalabbildung
. Die Diagonalabbildung ist ein Homomorphismus der Ringe und der Moduln. Dabei sind alle Komponenten von
ist ein Homomorphismus der Ringe und der Moduln. Dabei sind alle Komponenten von  gleich r.
gleich r.
- Ist
 eine Familie von Untermoduln, so gibt es einen eindeutig bestimmten Homomorphismus
eine Familie von Untermoduln, so gibt es einen eindeutig bestimmten Homomorphismus  mit
mit  . Dabei ist
. Dabei ist  die Familie der kanonischen Homomorphismen von
die Familie der kanonischen Homomorphismen von  auf die Faktormoduln
auf die Faktormoduln  . Der Kern dieses Homomorphismus ist
. Der Kern dieses Homomorphismus ist  .
.
- Sind
 und
und  zwei Familien von Moduln und ist
zwei Familien von Moduln und ist  eine Familie von Homomorphismen, so ist die Abbildung
eine Familie von Homomorphismen, so ist die Abbildung  ein Homomorphismus. Es ist
ein Homomorphismus. Es ist  . Weiter ist
. Weiter ist  .
.
- Ist auch
 eine Familie von Moduln und ist für alle
eine Familie von Moduln und ist für alle  die Folge
die Folge  exakt, so ist
exakt, so ist  exakt.
exakt.
- Sind
 Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus
Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus  mit
mit  für alle
für alle  . Es ist
. Es ist  . Ist
. Ist  der Endomorphismenring von
der Endomorphismenring von  , so ist
, so ist  auf der linken Seite ein S– Untermodul von
auf der linken Seite ein S– Untermodul von  . Ist
. Ist  so koerzeugt der Modul
so koerzeugt der Modul  den Modul
den Modul  . Ein Modul, der alle Rechtsmoduln koerzeugt heißt Kogenerator. Der Modul
. Ein Modul, der alle Rechtsmoduln koerzeugt heißt Kogenerator. Der Modul  ist daher ein Kogenerator, wenn es zu jedem Rechtsmodul
ist daher ein Kogenerator, wenn es zu jedem Rechtsmodul  einen Monomorphismus
einen Monomorphismus  gibt, für eine gewisse Indexmenge
gibt, für eine gewisse Indexmenge  [2].
[2].
- Ist
 eine abelsche Gruppe, so ist
eine abelsche Gruppe, so ist  torsionsfrei genau dann, wenn
torsionsfrei genau dann, wenn  von
von  koerzeugt wird.[3]
koerzeugt wird.[3]
 ist ein Kogenerator in der Kategorie der abelschen Gruppen. Dies ist nicht mehr ganz einfach. Es setzt die Theorie der injektiven Moduln voraus. Siehe dazu zum Beispiel[4]
ist ein Kogenerator in der Kategorie der abelschen Gruppen. Dies ist nicht mehr ganz einfach. Es setzt die Theorie der injektiven Moduln voraus. Siehe dazu zum Beispiel[4]
Eine Funktion  heißt endlichwertig, wenn
heißt endlichwertig, wenn  nur für endlich viele
nur für endlich viele  gilt. Man meint dasselbe, wenn man sagt
gilt. Man meint dasselbe, wenn man sagt  für fast alle
für fast alle  . Die Menge der endlichwertigen Abbildungen aus
. Die Menge der endlichwertigen Abbildungen aus  wird Koprodukt (oder äußere direkte Summe) der Familie
wird Koprodukt (oder äußere direkte Summe) der Familie  genannt und mit
genannt und mit  bezeichnet.
bezeichnet.  ist ein Untermodul des Produktes.
ist ein Untermodul des Produktes.
Ist  , so sei
, so sei  die folgende Abbildung aus
die folgende Abbildung aus  :
:

Schreibt man die Abbildung  als Tupel, so ist
als Tupel, so ist  . An allen Stellen des Tupels steht 0 nur an der j-ten Stelle steht a.
. An allen Stellen des Tupels steht 0 nur an der j-ten Stelle steht a.
 ist der einzige Homomorphismus
ist der einzige Homomorphismus  , welcher folgende Bedingung erfüllt:
, welcher folgende Bedingung erfüllt:
Dies ergibt sich aus der universellen Eigenschaft des Produktes.
Die  sind alles Monomorphismen und es ist
sind alles Monomorphismen und es ist  die direkte Summe der
die direkte Summe der  in dem Produkt der
in dem Produkt der  .
.
Ist  das Koprodukt der Moduln
das Koprodukt der Moduln  so bilden die Funktionen
so bilden die Funktionen

die  monomorph nach
monomorph nach  ab. Sie heißen Injektionen.
Das Paar
ab. Sie heißen Injektionen.
Das Paar  hat die folgende Eigenschaft:
hat die folgende Eigenschaft:
Zu jedem Modul  und jeder Familie von Homomorphismen
und jeder Familie von Homomorphismen  gibt es genau einen Homomorphismus
gibt es genau einen Homomorphismus  , so dass
, so dass  für alle
für alle  gilt.
gilt.
In der Kategorientheorie kennzeichnet diese universelle Eigenschaft das Koprodukt von Objekten bis auf Isomorphie, das heißt:
Ist  ein Modul und
ein Modul und  eine Familie von Homomorphismen und gibt es zu jedem Modul
eine Familie von Homomorphismen und gibt es zu jedem Modul  und jeder Familie
und jeder Familie  von Homomorphismen genau ein
von Homomorphismen genau ein  mit
mit  , so ist
, so ist  .
.
Die oben angegebene Konstruktion zusammen mit dem Nachweis der universellen Eigenschaft fasst man auch kurz so zusammen: In der Kategorie der Moduln gibt es Koprodukte.
Ist  eine Familie von Homomorphismen, so ist
eine Familie von Homomorphismen, so ist
 genau dann ein Koprodukt der Familie
genau dann ein Koprodukt der Familie  , wenn der
Homomorphismus
, wenn der
Homomorphismus

für alle Rechtsmoduln  ein Isomorphismus ist. Insbesondere ist:
ein Isomorphismus ist. Insbesondere ist:

ein  funktorieller Isomorphismus.
funktorieller Isomorphismus.
- Meist identifiziert man die
 mit den
mit den  in
in  . Dann schreibt man
. Dann schreibt man  anstelle von
anstelle von  . Normalerweise ist keine Verwechslung zu befürchten.
. Normalerweise ist keine Verwechslung zu befürchten.
- Ist
 für alle
für alle  so schreibt man
so schreibt man  anstelle von
anstelle von  .
.
- Ist
 für alle
für alle  , so ist
, so ist  ein freier Modul. Eine Basis ist die Familie
ein freier Modul. Eine Basis ist die Familie  mit
mit  .
.
- Ist die Indexmenge
 endlich, so sind direkte Summe und direktes Produkt identisch.
endlich, so sind direkte Summe und direktes Produkt identisch.
- Ist
 eine endliche Teilmenge von
eine endliche Teilmenge von  und
und  , so ist
, so ist  direkter Summand in
direkter Summand in  . Der Homomorphismus
. Der Homomorphismus  erfüllt die Bedingungen
erfüllt die Bedingungen  und
und  . Für unendliche Mengen ist die direkte Summe normalerweise keineswegs direkter Summand im direkten Produkt. So ist
. Für unendliche Mengen ist die direkte Summe normalerweise keineswegs direkter Summand im direkten Produkt. So ist  kein direkter Summand in
kein direkter Summand in  . Eine schwierige Frage ist: Für welche Moduln
. Eine schwierige Frage ist: Für welche Moduln  ist
ist  direkter Summand im Produkt
direkter Summand im Produkt  ? Ist beispielsweise
? Ist beispielsweise  halbeinfach und endlich erzeugt, so ist dies der Fall.
halbeinfach und endlich erzeugt, so ist dies der Fall.
- Sind
 Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus
Rechtsmoduln, so gibt es einen eindeutig bestimmten Homomorphismus  mit
mit  für alle
für alle  . Es ist
. Es ist  . Ist
. Ist  der Endomorphismenring von
der Endomorphismenring von  , so ist
, so ist  auf der linken Seite ein S– Untermodul von
auf der linken Seite ein S– Untermodul von  . Ist
. Ist  , so erzeugt der Modul
, so erzeugt der Modul  den Modul
den Modul  . Ein Modul, der alle Rechtsmoduln erzeugt heißt Generator. Der Modul
. Ein Modul, der alle Rechtsmoduln erzeugt heißt Generator. Der Modul  ist daher ein Generator, wenn es zu jedem Rechtsmodul
ist daher ein Generator, wenn es zu jedem Rechtsmodul  einen Epimorphismus
einen Epimorphismus  gibt, für eine gewisse Indexmenge
gibt, für eine gewisse Indexmenge  . Da jeder Modul das epimorphe Bild eines freien Moduls ist, ist
. Da jeder Modul das epimorphe Bild eines freien Moduls ist, ist  ein Generator.
ein Generator.
Sei  eine unendliche Kardinalzahl. Ist der Modul
eine unendliche Kardinalzahl. Ist der Modul  direkte Summe von
direkte Summe von  erzeugbaren Untermoduln, so ist jeder direkte Summand von
erzeugbaren Untermoduln, so ist jeder direkte Summand von  direkte Summe von
direkte Summe von  erzeugbaren Untermoduln.
erzeugbaren Untermoduln.
Der wichtigste Fall ist: Ist  direkte Summe von abzählbar erzeugten Untermoduln, so hat jeder direkte Summand diese Eigenschaft. In dieser Form hat Irving Kaplansky den Satz ursprünglich bewiesen. Daraus folgt beispielsweise, dass jeder projektive Modul direkte Summe von abzählbar erzeugten Moduln ist. Will man daher Struktursätze über projektive Moduln beweisen, so kann man sich dank Kaplansky auf abzählbar erzeugte beschränken. Jeder projektive Modul ist ja direkter Summand in einem freien Modul.
direkte Summe von abzählbar erzeugten Untermoduln, so hat jeder direkte Summand diese Eigenschaft. In dieser Form hat Irving Kaplansky den Satz ursprünglich bewiesen. Daraus folgt beispielsweise, dass jeder projektive Modul direkte Summe von abzählbar erzeugten Moduln ist. Will man daher Struktursätze über projektive Moduln beweisen, so kann man sich dank Kaplansky auf abzählbar erzeugte beschränken. Jeder projektive Modul ist ja direkter Summand in einem freien Modul.
Seien  zwei Zerlegungen von
zwei Zerlegungen von  . Sind die Endomorphismenringe aller
. Sind die Endomorphismenringe aller  lokal und sind alle
lokal und sind alle  unzerlegbar, so gibt es eine Bijektion
unzerlegbar, so gibt es eine Bijektion  mit
mit  für alle
für alle  .
.
Dieser Satz verallgemeinert viele wichtige Sätze. So zum Beispiel:
- Je zwei Basen eines Vektorraumes haben gleiche Mächtigkeit.
- Die Zerlegung eines halbeinfachen Moduls in eine direkte Summe von einfachen Moduln ist im Sinne des Satzes eindeutig.
- Der Zerlegungssatz von Satz von Krull-Remak-Schmidt für Moduln endlicher Länge.
- ↑ Friedrich Kasch Moduln und Ringe. Teubner, Stuttgart 1977, Seite 77 ISBN 3-519-02211-7
- ↑ Robert Wisbauer, Grundlagen der Modul – und Ringtheorie, Verlag Reinhard Fischer, München 1988 Seite 112 ISBN 3-88927-044-1
- ↑ Frank W. Anderson, Kent R. Fuller, Rings and Categories of modules Springe, New York Berlin Heidelberg, 1992, Seite 106, ISBN 0-387-97845-3
- ↑ Friedrich Kasch Moduln und Ringe. Teubner, Stuttgart 1977, Seite 127 ISBN 3-519-02211-7
- Frank W. Anderson and Kent R. Fuller: Rings and Categories of Modules. Springer, New-York 1992, ISBN 0-387-97845-3
- Friedrich Kasch: Moduln und Ringe. Teubner, Stuttgart 1977, ISBN 3-519-02211-7
- Robert Wisbauer: Grundlagen der Modul- und Ringtheorie. Reinhard Fischer, München 1988, ISBN 3-88927-044-1