Blockplan
Ein Blockplan (auch Block-Design oder kombinatorisches Design) ist eine endliche Inzidenzstruktur, die insbesondere in der endlichen Geometrie, der Kombinatorik sowie der statistischen Versuchsplanung von Bedeutung ist. Blockpläne sind eine gemeinsame Verallgemeinerung der endlichen affinen Ebenen und der endlichen projektiven Ebenen.
Wichtige Methoden zur Charakterisierung von Blockplänen und zur Konstruktion neuer Blockpläne aus bekannten sind die Auflösung und die taktische Zerlegung eines Blockplanes. Die Auflösung verallgemeinert das Konzept des Parallelismus eines Blockplanes, wie es dieser Artikel beschreibt, und ist selbst ein Spezialfall der taktischen Zerlegung.
Definitionen und Schreibweisen
[Bearbeiten | Quelltext bearbeiten]Sei eine endliche Inzidenzstruktur, bei der die Elemente von als Punkte und die Elemente von als Blöcke bezeichnet werden. Des Weiteren seien natürliche Zahlen, dann wird die Inzidenzstruktur als -Blockplan bezeichnet, wenn die folgenden Axiome gelten:[1][2]
- (B1) hat genau Punkte, also ,
- (B2) jeder Block von inzidiert mit genau Punkten, also ,
- (B3) für jede Punktmenge mit verschiedenen Punkten existieren genau verschiedene Blöcke, die jeweils mit allen Punkten von inzidieren, also und
- (B4) , das heißt, ist eine nichtausgeartete oder echte Inzidenzstruktur.
Als alternative Bezeichnung für einen -Blockplan wird auch verwendet. Im Falle von schreibt man auch einfach und spricht von einem Steinersystem (nach Jakob Steiner). Ein -Blockplan () wird auch als Steiner-Tripel-System bezeichnet.[3] Teilweise wird ein Blockdesign auch als geschrieben, der zusätzliche Parameter wird weiter unten erläutert.
Einen -Blockplan bezeichnet man oft kurz auch -Blockplan und einen -Blockplan einfach als Blockplan, da der am meisten verwendete Fall ist.
Die konstante Anzahl aller Blöcke von durch einen Punkt von wird mit bezeichnet und die Anzahl aller Blöcke von mit .
In Anlehnung an bestimmte geometrische Modelle für einen Blockplan werden seine Blöcke gelegentlich auch als Geraden, Kreise, Ebenen oder Ähnliches bezeichnet. Wenn ein Punkt mit einem Block inzidiert, also , so sind auch die folgen Sprechweisen üblich: liegt auf oder geht durch . Inzidiert ein Punkt mit mehreren Blöcken, so sagt man auch, dass die Blöcke sich in schneiden.
Blockpläne, bei denen ein Block mit allen Punkten inzidiert, oder bei denen die -elementigen Teilmengen der Punktmenge genau den Blöcken entsprechen, werden als triviale Blockpläne bezeichnet.
Ein Block muss formal von der mit ihm inzidierenden Punktmenge unterschieden werden, allerdings ist es in der Praxis meist möglich, einen Block mit seiner inzidierenden Punktmenge zu identifizieren und die Inzidenzrelation als mengentheoretisches Enthaltensein zu interpretieren. Solche Blockpläne werden auch als einfach bezeichnet (vgl. die Beispiele im Artikel „Inzidenzstruktur“).
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Für die Anzahl der Blöcke eines -Blockplans gilt:
- .
Mit für bezeichnet man die Anzahl der Blöcke, die mit allen Punkten einer beliebigen Punktmenge mit Punkten inzidieren, also , für diese gilt:
- .
Ein Blockplan mit gegebenen Parametern kann nur dann existieren, wenn diese ganze Zahlen sind. Dies nennt man die Teilbarkeitsbedingungen für die Existenz von Blockplänen.
Für -Blockpläne ergibt sich aus den beiden Formeln unter Berücksichtigung von :
- .
Außerdem gilt für die -Blockpläne die Fisher-Ungleichung:[4]
- .
Neben den unten bei den Beispielen erwähnten, endlichen, projektiven und affinen Räumen stehen Blockpläne in Wechselbeziehungen zu vielen anderen Strukturen der Kombinatorik. So ist zum Beispiel die Existenz eines -Blockplans mit äquivalent zur Existenz einer Hadamard-Matrix der Ordnung . Aus diesem Grund werden solche Blockpläne auch als Hadamard-Blockpläne bezeichnet. Den Zusammenhang zwischen Codes und Blockplänen beschreibt der Satz von Assmus-Mattson.
Eine zentrale Frage in der Theorie der Blockpläne ist, für welche Werte der Parameter überhaupt ein Blockplan existiert. Ein bahnbrechendes Ergebnis von Peter Keevash (2014) zeigt, dass die Teilbarkeitsbedingungen für die Existenz hinreichend sind, wenn die Zahl der Punkte genügend groß ist.[5][6][7][8]
Außerdem gibt es eine Reihe von notwendigen Kriterien für die Existenz bestimmter Blockpläne, mit denen man viele Parameterkombinationen ausschließen kann. Solche Kriterien liefern zum Beispiel die verallgemeinerte Fisher-Ungleichung (auch Satz von Ray-Chaudhuri-Wilson genannt) und der Satz von Bruck-Ryser-Chowla.
Symmetrische Blockpläne
[Bearbeiten | Quelltext bearbeiten]Ein Blockplan, der genauso viele Blöcke wie Punkte besitzt , wird als symmetrisch oder projektiv bezeichnet. Symmetrische Blockpläne können unter den 2-Blockplänen durch verschiedene, gleichwertige Aussagen charakterisiert werden: Sei ein -Blockplan, sei die Gesamtzahl seiner Blöcke und sei eine Inzidenzmatrix dieses Blockplanes. Dann sind die folgenden Aussagen gleichwertig:[9]
- Die Anzahl der Punkte ist gleich der Anzahl der Blöcke und damit gilt auch , das heißt ist symmetrisch. Es gilt
- Die Zahl der Blöcke, mit denen ein beliebiger Punkt inzidiert, ist gleich der Zahl der Punkte, mit denen ein beliebiger Block inzidiert .
- hierbei ist die -Einheitsmatrix, die -Einsmatrix
- hierbei ist die -Einheitsmatrix, die -Einsmatrix
- Je zwei verschiedene Blöcke schneiden sich in genau Punkten.
- Je zwei verschiedene Blöcke haben eine konstante, positive Anzahl von Punkten gemeinsam, das heißt, erfüllt die Regularitätsbedingung . Siehe Regularitätsbedingungen und Typen von endlichen Inzidenzstrukturen.
- hat als Inzidenzstruktur den Typ , das heißt, erfüllt die Regularitätsbedingungen .
Das Intervall, in dem die Anzahl der Punkte (bzw. Blöcke) in Bezug auf die Ordnung eines symmetrischen -Blockplans variiert, ergibt sich als , sofern ein nicht trivialer Blockplan mit vorliegt. Der untere Extremalfall ist gegeben für Hadamard-Blockpläne und der obere Extremalfall für die endlichen projektiven Ebenen.[10][11]
Parallelismen und affine Blockpläne
[Bearbeiten | Quelltext bearbeiten]Ein Parallelismus eines Blockplans ist eine Äquivalenzrelation auf der Menge der Blöcke, für die das euklidische Parallelenpostulat gilt:
- Zu jedem Block und jedem Punkt gibt es genau einen Block inzident mit der zu parallel ist.
Hierbei werden Blöcke als parallel (Schreibweise ) bezeichnet, wenn sie in derselben Äquivalenzklasse liegen. Die Äquivalenzklassen selbst werden auch als Parallelenklassen oder Parallelenscharen bezeichnet. Für zwei parallele Blöcke gilt, dass sie (genauer: die mit ihnen inzidierenden Punktmengen) entweder identisch oder disjunkt sind:
- .
Ein Parallelismus eines Blockplans, bei dem zwei beliebige, nicht parallele Blöcke stets dieselbe Anzahl von Punkten gemeinsam haben, heißt affin und der zugehörige Blockplan wird als affiner Blockplan bezeichnet. Während im Allgemeinen ein Blockplan mehrere Parallelismen zulassen kann, ist in einem affinen Blockplan der Parallelismus eindeutig bestimmt und es gilt auch die Umkehrung der obigen Beziehung:
- .
Für Blockpläne mit Parallelismen gilt der Satz von Bose, der für diesen Fall eine Verschärfung der Fisher-Ungleichung darstellt.
Beispiele
[Bearbeiten | Quelltext bearbeiten]Die Wittschen Blockpläne (im engeren Sinn) sind einfache 5-Blockpläne, ihre Ableitungen, die oft auch als Wittsche Blockpläne bezeichnet werden, liefern Beispiele für nichttriviale einfache 4- und 3-Blockpläne.
Affine Geometrien als Blockpläne
[Bearbeiten | Quelltext bearbeiten]Der affine Raum der Dimension über dem endlichen Körper mit Elementen wird als notiert.[12] Er wird zu einem Blockplan , indem man die Punktmenge des affinen Raumes als Menge der Punkte und die -dimensionalen affinen Teilräume als Blöcke verwendet. Genauer handelt es sich bei um einen -Blockplan. Der gewöhnliche Parallelismus der affinen Geometrie ist ein Parallelismus für den Blockplan und der Blockplan wird damit genau dann zu einem affinen Blockplan, wenn gilt, also die Blöcke Hyperebenen des Raumes sind. Die Parameter des Blockplanes lauten:
- .
Hier steht für den Gaußschen Binomialkoeffizienten,[12] der durch die Formel
für berechnet werden kann. Die Räume sind für sogar 3-Blockpläne mit . Speziell ist mit seinem geometrischen Parallelismus ein affiner -Blockplan.
Projektive Geometrien als Blockpläne
[Bearbeiten | Quelltext bearbeiten]Der projektive Raum der Dimension über dem endlichen Körper wird als notiert.[12][13] Der Blockplan hat als Punktmenge die Menge der projektiven Punkte und als Blockmenge die Menge der -dimensionalen projektiven Teilräume des . Dies ist ein -Blockplan mit den Parametern
- .
Im Falle also falls die Blöcke die Hyperebenen des Raumes sind, ist der Blockplan symmetrisch.
Anschauliche Beispiele
[Bearbeiten | Quelltext bearbeiten]Als Spezialfälle der obengenannten klassischen geometrischen Räume kann man eine endliche projektive Ebene der Ordnung als einen -Blockplan und eine endliche affine Ebene der Ordnung als einen -Blockplan auffassen. Hierbei entsprechen die Punkte der Ebene den Punkten des Blockplans und die Geraden der Ebene den Blöcken des Blockplans. Allerdings wird die Existenz der entsprechenden Ebene der Ordnung vorausgesetzt und diese ist nicht für alle gegeben.
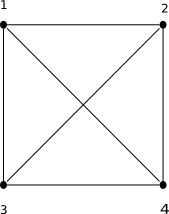
Kleine Ebenen, siehe auch die Abbildungen am Ende des Abschnitts:
- Die projektive Ebene der Ordnung 2, (die Fano-Ebene) ist ein symmetrischer -Blockplan zugleich ist sie „der“ kleinste Hadamard-Blockplan.
- Die affinen Ebenen der Ordnung 2 und 3 und bilden mit ihrer gewöhnlichen und einzig möglichen Parallelität einen affinen -Blockplan bzw. -Blockplan.
| 7 Pkte, 7 Blöcke mit je 3 Pkten | 4 Pkte, 6 Blöcke mit je 2 Pkten | 9 Pkte, 12 Blöcke mit je 3 Pkten |
Weitere (Gegen)beispiele einfacher Blockpläne
[Bearbeiten | Quelltext bearbeiten]Nicht existierende einfache 2-Blockpläne
[Bearbeiten | Quelltext bearbeiten]Für die in der folgenden Liste erscheinenden Parametertripel (im Bereich ) existieren keine einfachen -Blockpläne, obwohl die üblichen Parameterbedingungen erfüllt sind:[14]
Existierende einfache t-Blockpläne mit t ≥ 4
[Bearbeiten | Quelltext bearbeiten]Konkrete Beispiele für einfache -Blockpläne mit waren lange nur vereinzelt bekannt.
- und
- und
- und
- und
- und
- und
Bis in die 1980er Jahre war sogar unklar, ob (etwa) einfache -Blockpläne überhaupt vorkommen. Dann wurden nach und nach mehrere Beispiele gefunden:[17][19]
- und
- und
- und
- und
- und
In den letzten Jahren ist mit Hilfe weiter verfeinerter gruppentheoretischer, geometrischer und computergestützter Methoden schließlich sogar eine Anzahl einfacher Blockpläne mit gefunden worden; u. a. :[20]
- und
- und
Anwendung in der statistischen Versuchsplanung
[Bearbeiten | Quelltext bearbeiten]Angenommen, Hautkrebsforscher möchten drei verschiedene Sonnencremes testen. Dafür tragen sie bei jedem Probanden zwei verschiedene Sonnencremes auf die Oberseiten der Hände auf. Nach einer Bestrahlung durch UV-Licht notieren sie die aufgetretenen Hautirritationen in Form von Sonnenbrand. Die Anzahl der Behandlungen ist 3 (Sonnencremes) und die Blockgröße ist 2 (Hände je Person).
Ein dazu passender balancierter unvollständiger Versuchsplan kann in R erzeugt werden mit der Funktion design.bib aus dem R-Paket agricolae[21] und wird in der folgenden Tabelle dargestellt:
| Plots | Block | Treatment |
|---|---|---|
| 101 | 1 | 3 |
| 102 | 1 | 1 |
| 201 | 2 | 1 |
| 202 | 2 | 2 |
| 301 | 3 | 3 |
| 302 | 3 | 2 |
| 401 | 4 | 3 |
| 402 | 4 | 1 |
| 501 | 5 | 2 |
| 502 | 5 | 3 |
| 601 | 6 | 1 |
| 602 | 6 | 2 |
Die Forscher wählen die Parameter und für den Blockplan, welche anschließend in die R-Funktion eingegeben werden. Dann werden die verbliebenen Parameter und automatisch ermittelt.
Mit den Bezeichnungen bis für die Blöcke erhält man die folgende Inzidenzmatrix:
| Behandlung | Block A | Block B | Block C | Block D | Block E | Block F |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 1 | 1 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 | 1 | 1 | 0 |
Jede Behandlung kommt in vier Blöcken vor, also ist .
Zwei Blöcke ( und ) enthalten gleichzeitig die Behandlungen und und entsprechendes gilt auch für die Behandlungspaare und . Demnach ist .
Es ist in diesem Beispiel unmöglich einen vollständigen Versuchsplan zu erhalten (alle Behandlungen in jedem Block), weil drei Sonnencremes getestet werden, aber nur zwei Hände je Person zur Verfügung stehen.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Thomas Beth, Dieter Jungnickel, Hanfried Lenz: Design Theory. 2. Auflage. B.I. Wissenschaftsverlag, London/New York/New Rochelle/Melbourne/Sidney 1999, ISBN 0-521-33334-2 (Erstausgabe: 1986).
- Albrecht Beutelspacher: Einführung in die endliche Geometrie. I. Blockpläne. B.I. Wissenschaftsverlag, Mannheim/Wien/Zürich 1982, ISBN 3-411-01632-9.
- Daniel R. Hughes, Fred C. Piper: Design Theory. Cambridge University Press, Cambridge (u. a.) 1985, ISBN 0-521-25754-9.
- Jacobus Hendricus Van Lint, Richard Michael Wilson: A Course in Combinatorics. Cambridge University Press, 1992, ISBN 0-521-42260-4, S. 188.
- Kenneth H. Rosen (Hrsg.): Handbook of Discrete and Combinatorial Mathematics. CRC Press, 2000, ISBN 0-8493-0149-1.
- Tosiro Tsuzuku: Finite Groups and Finite Geometries (= Cambridge Tracts in Mathematics. Band 78). Cambridge University Press, Cambridge (u. a.) 1982, ISBN 0-521-22242-7.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: block design. In: MathWorld (englisch).
- Skript Algebraische Strukturen und Diskrete Mathematik. (PDF; 1,01 MB) S. 67
- block design in der Encyclopaedia of Mathematics
- Publikationen der Universität Bayreuth
- Charles Colbourn, Jeff Dinitz: Handbook of Combinatorial Designs
Einzelnachweise und Anmerkungen
[Bearbeiten | Quelltext bearbeiten]- ↑ Beutelspacher (1982)
- ↑ Die in Klammern angegebenen zusätzlichen Parameternamen sind die allgemein für die Parameter einer endlichen Inzidenzstruktur üblichen.
- ↑ Beth, Jungnickel, Lenz (1986, 1999), Definition I.3.1
- ↑ Beth, Jungnickel, Lenz (1986, 1999), Corollary I.8.6
- ↑ Peter Keevash: The existence of designs. arXiv, 2014.
- ↑ A Design Dilemma Solved, Minus Designs. Quanta Magazine, 9. Juni 2015, abgerufen am 27. Juni 2015.
- ↑ Gil Kalai: Designs exist! In: bourbaki.ens.fr. Séminaire BOURBAKI
- ↑ Timothy Gowers: PROBABILISTIC COMBINATORICS AND THE RECENT WORK OF PETER KEEVASH. BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY, Band 54, Nr. 1, Januar 2017, S. 107–116, doi:10.1090/bull/1553.
- ↑ Beutelspacher 1.4.4.
- ↑ Kenneth H. Rosen (Hrsg.): Handbook of Discrete and Combinatorial Mathematics. CRC Press, 2000, ISBN 0-8493-0149-1, S. 771.
- ↑ Tosiro Tsuzuku: Finite Groups and Finite Geometries (= Cambridge Tracts in Mathematics. Band 78). Cambridge University Press, Cambridge (u. a.) 1982, ISBN 0-521-22242-7, S. 62.
- ↑ a b c Beth, Jungnickel, Lenz (1986, 1999), I.Examples and basic definitions
- ↑ Bei symmetrischen Blockplänen verweist der Parameter in der Regel auf die Blockplanordnung . Die hier genannte Dimensionszahl ist mit der Blockplanordnung im Allgemeinen nicht identisch.
- ↑ Rosen et al.: Handbook ... S. 764,773.
- ↑ Also existiert auch nicht die projektive Ebene der Ordnung 6.
- ↑ Also existiert auch nicht die projektive Ebene der Ordnung 10.
- ↑ a b Kenneth H. Rosen (Hrsg.): Handbook of Discrete and Combinatorial Mathematics. CRC Press, 2000, ISBN 0-8493-0149-1, S. 767.
- ↑ Daniel R. Hughes, Fred C. Piper: Design Theory. Cambridge University Press, Cambridge (u. a.) 1985, ISBN 0-521-25754-9, S. 144 ff.
- ↑ Daniel R. Hughes, Fred C. Piper: Design Theory. Cambridge University Press, Cambridge (u. a.) 1985, ISBN 0-521-25754-9, S. 148, 152.
- ↑ Siehe Weblink zu den Publikationen der Universität Bayreuth.
- ↑ Felipe de Mendiburu: agricolae: Statistical Procedures for Agricultural Research. 12. Juni 2016, abgerufen am 19. Februar 2017.
















































































![{\displaystyle \textstyle \left[{n \atop i}\right]_{q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bfae3da222bea79b0bde4564662cc24a3eae6a)