Turinggrad
In der Berechenbarkeitstheorie und der mathematischen Logik misst der Turinggrad (auch Grad der Unlösbarkeit) einer Menge natürlicher Zahlen die algorithmische Unlösbarkeit der Menge. Das Konzept des Turinggrades ist fundamental in der Berechenbarkeitstheorie, wo Mengen natürlicher Zahlen oft als Entscheidungsprobleme angesehen werden; der Turinggrad einer Menge gibt an, wie schwer das Entscheidungsproblem für die Menge ist.
Zwei Mengen sind Turing-äquivalent, wenn sie den gleichen Grad der Unlösbarkeit haben; jeder Turinggrad ist eine Menge Turing-äquivalenter Mengen, sodass zwei Mengen genau dann in unterschiedlichen Turinggraden liegen, wenn sie nicht Turing-äquivalent sind. Außerdem sind die Turinggrade im folgenden Sinne partiell geordnet: Wenn der Turinggrad einer Menge kleiner als der Turinggrad einer Menge ist, dann kann jede (unberechenbare) Prozedur, die korrekt entscheidet, ob Zahlen in liegen, berechenbar in eine Prozedur umgewandelt werden, die korrekt entscheidet, ob Zahlen in liegen. In diesem Sinne korrespondiert der Turinggrad einer Menge mit dem Grad ihrer algorithmischen Unlösbarkeit.
Die Turinggrade wurden 1944 von Emil Leon Post eingeführt, und viele grundlegende Resultate wurden 1954 von Stephen Cole Kleene und Post bewiesen. Die Turinggrade sind bis heute Gegenstand intensiver Forschung. Viele Beweise in diesem Gebiet benutzen eine Beweistechnik, die als Prioritätsmethode bekannt ist.
Turing-Äquivalenz
[Bearbeiten | Quelltext bearbeiten]Im Folgenden bezieht sich das Wort Menge auf Teilmengen natürlicher Zahlen. Eine Menge heißt Turing-reduzierbar auf eine Menge , wenn es eine Orakel-Turingmaschine gibt, die mit Hilfe eines Orakels für entscheidet, ob eine gegebene Zahl in liegt. Die Notation steht für: ist auf Turing-reduzierbar.
Zwei Mengen und heißen Turing-äquivalent, wenn sie aufeinander Turing-reduzierbar sind. Die Notation steht für: und sind Turing-äquivalent. Die Relation ist eine Äquivalenzrelation.
Turinggrad
[Bearbeiten | Quelltext bearbeiten]Ein Turinggrad ist eine Äquivalenzklasse der Relation . Die Notation bezeichnet die Äquivalenzklasse, die die Menge enthält. Die Klasse aller Turinggrade wird mit bezeichnet.
Die Turinggrade haben eine partielle Ordnung . Sie ist so definiert, dass genau dann gilt, wenn . Es gibt einen Turinggrad, der genau die entscheidbaren Mengen enthält, und dieser Grad ist kleiner als alle anderen. Er wird mit (Null) bezeichnet, da er das kleinste Element der partiell geordneten Menge ist. Turinggrade werden meist durch Fettdruck bezeichnet, um sie von Mengen zu unterscheiden. Als Variablen für Turinggrade dienen fette kleine Buchstaben etc.
Für alle Mengen und ist (gesprochen join) die Vereinigung der Mengen und . Der Turinggrad von ist das Supremum der Grade und . Damit ist ein oberer Halbverband. Das Supremum der Grade und wird mit bezeichnet. Es ist bekannt, dass kein Verband ist, da es Paare von Graden ohne Infimum gibt.
Für jede Menge bezeichnet die Menge der Indizes von Orakelmaschinen, die auf ihrem eigenen Index als Eingabe halten, wenn sie als Orakel benutzen. Die Menge wird als Turing-Sprung von bezeichnet. Der Turing-Sprung eines Grades ist der Grad ; dies ist wohldefiniert, da aus folgt. Ein wichtiges Beispiel ist , der Grad des Halteproblems.
Grundlegende Eigenschaften der Turinggrade
[Bearbeiten | Quelltext bearbeiten]- Jeder Turinggrad ist abzählbar unendlich, das heißt, er enthält genau Mengen.
- Es gibt (siehe Beth-Funktion) verschiedene Turinggrade.
- Für jeden Grad gilt die strikte Ungleichung .
- Für jeden Grad ist die Menge der Grade unter höchstens abzählbar. Die Menge der Grade über hat Mächtigkeit .
Struktur der Turinggrade
[Bearbeiten | Quelltext bearbeiten]Die Struktur der Turinggrade wurde intensiv erforscht. Die folgende Liste gibt nur wenige der vielen bekannten Ergebnisse an. Generell lässt sich aus den bekannten Ergebnissen schließen, dass die Struktur der Turinggrade sehr kompliziert ist.
Ordnungseigenschaften
[Bearbeiten | Quelltext bearbeiten]- Es gibt minimale Grade. Ein Grad heißt minimal, wenn ungleich ist und es keinen Grad zwischen und gibt. Damit ist die Ordnung der Grade nicht dicht.
- Für jeden Grad ungleich gibt es einen Grad , der mit nicht vergleichbar ist.
- Es gibt untereinander nicht vergleichbare Turinggrade.
- Es gibt Paare von Graden ohne Infimum. Damit ist kein Verband.
- Jede abzählbare partielle Ordnung lässt sich in die Turinggrade einbetten.
- Keine unendliche, strikt aufsteigende Folge von Graden hat ein Supremum.
Eigenschaften des Sprungoperators
[Bearbeiten | Quelltext bearbeiten]- Für jeden Grad gibt es einen Grad zwischen und . Es gibt sogar eine abzählbar unendliche Folge paarweise nicht vergleichbarer Grade zwischen und .
- Ein Grad hat die Form für ein genau dann, wenn gilt.
- Für jeden Grad gibt es einen Grad , sodass und . Solch ein Grad heißt niedrig relativ zu .
- Es gibt eine unendliche Folge von Graden, sodass für alle .
Logische Eigenschaften
[Bearbeiten | Quelltext bearbeiten]- Simpson (1977) zeigte, dass die Theorie von in der Prädikatenlogik erster Stufe in der Sprache oder many-one-äquivalent zur Theorie der natürlichen Zahlen in der Prädikatenlogik zweiter Stufe ist.
- Shore und Slaman (1999) zeigten, dass sich der Sprungoperator in der Struktur der Grade in der Logik erster Stufe mit der Sprache definieren lässt.
Struktur der rekursiv aufzählbaren Turinggrade
[Bearbeiten | Quelltext bearbeiten]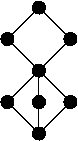
Ein Grad heißt rekursiv aufzählbar, wenn er eine rekursiv aufzählbare Menge enthält. Jeder rekursiv aufzählbare Grad ist kleiner oder gleich , aber nicht jeder Grad kleiner ist rekursiv aufzählbar.
- (Satz von Friedberg und Muchnik, 1956) Es gibt rekursiv aufzählbare Grade zwischen und .
- (G. E. Sacks, 1964) Die rekursiv aufzählbaren Grade sind dicht, das heißt, zwischen zwei rekursiv aufzählbaren Graden existiert immer ein dritter rekursiv aufzählbarer Grad.
- (A. H. Lachlan, 1966a und C. E. M. Yates, 1966) Es gibt zwei rekursiv aufzählbare Grade, die kein Infimum in den rekursiv aufzählbaren Graden haben.
- (A. H. Lachlan, 1966a und C. E. M. Yates, 1966) Es gibt ein Paar von rekursiv aufzählbaren Graden ungleich , deren Infimum ist.
- (S. K. Thomason, 1971) Jeder endlicher distributiver Verband kann in die rekursiv aufzählbaren Grade eingebettet werden. Es ist sogar möglich, die abzählbare boolesche Algebra ohne Atome so einzubetten, dass Suprema und Infima erhalten bleiben.
- (A. H. Lachlan und R. I. Soare, 1980) Nicht alle endlichen Verbände können in die rekursiv aufzählbaren Grade eingebettet werden, sodass Suprema und Infima erhalten bleiben. So kann insbesondere der rechts abgebildete Verband nicht eingebettet werden.
- (A. H. Lachlan, 1966b) Es gibt kein Paar rekursiv aufzählbarer Grade, deren Infimum ist und deren Supremum ist,
- (L. A. Harrington und T. A. Slaman, siehe Nies, Shore und Slaman (1998)) Die Theorie der rekursiv aufzählbaren Grade in der Sprache in Logik erster Stufe ist many-one-äquivalent zur Theorie der Arithmetik in Logik erster Stufe.
Literatur
[Bearbeiten | Quelltext bearbeiten]Einführungen
[Bearbeiten | Quelltext bearbeiten]- S. B. Cooper: Computability Theory. Chapman & Hall/CRC, 2004, ISBN 1-58488-237-9.
- Nigel Cutland: Computability, An introduction to recursive function theory. Cambridge University Press, 1980, ISBN 0-521-29465-7.
- Klaus Heidler, Hans Hermes, Friedrich-K. Mahn.: Rekursive Funktionen. Mannheim – Wien – Zürich 1977.
- Hans Hermes: Aufzählbarkeit – Entscheidbarkeit – Berechenbarkeit. Einführung in die Theorie der rekursiven Funktionen. Berlin/ Göttingen/ Heidelberg 1961. (2. Auflage. 1971, als Heidelberger Taschenbuch).
- Stephen Kleene: Introduction to Metamathematics. North-Holland, 1952, ISBN 0-7204-2103-9.
- Michael Sipser: Introduction to the Theory of Computation. PWS Publishing, 1997, ISBN 0-534-94728-X. Part Two: Computability Theory, Chapters 3–6, S. 123–222.
Spezialwerke
[Bearbeiten | Quelltext bearbeiten]- Piergiorgio Odifreddi: Classical Recursion Theory. North-Holland 1989, ISBN 0-444-87295-7.
- P. Odifreddi: Classical Recursion Theory, Volume II. Elsevier, 1999, ISBN 0-444-50205-X.
- Hartley Rogers: Theory of recursive functions and effective computability. McGraw-Hill, 1967.
- G. Sacks: Higher Recursion Theory. Springer-Verlag, 1990, ISBN 3-540-19305-7.
- R. I. Soare: Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic. Springer-Verlag, 1987, ISBN 0-387-15299-7.
Forschungspapiere
[Bearbeiten | Quelltext bearbeiten]- Stephen Cole Kleene, Emil L. Post: The upper semi-lattice of degrees of recursive unsolvability. In: Annals of Mathematics. Second Series. Band 59, Nr. 3, 1954, ISSN 0003-486X, S. 379–407, doi:10.2307/1969708, JSTOR:1969708.
- A.H. Lachlan: Lower Bounds for Pairs of Recursively Enumerable Degrees. In: Proceedings of the London Mathematical Society. Band 3, Nr. 1, 1966, S. 537.
- A.H. Lachlan: The impossibility of finding relative complements for recursively enumerable degrees. In: J. Symb. Logic. Band 31, Nr. 3, 1966, S. 434–454, doi:10.2307/2270459, JSTOR:2270459.
- A.H. Lachlan, R.I. Soare: Not every finite lattice is embeddable in the recursively enumerable degrees. In: Advances in Math. Band 37, 1980, S. 78–82, doi:10.1016/0001-8708(80)90027-4.
- André Nies, Richard A. Shore, Theodore A. Slaman: Interpretability and definability in the recursively enumerable degrees. In: Proc. London Math. Soc. (3). Band 77, Nr. 2, 1998, ISSN 0024-6115, S. 241–291, doi:10.1112/S002461159800046X.
- Emil L. Post: Recursively enumerable sets of positive integers and their decision problems. In: Bulletin of the American Mathematical Society. Band 50, Nr. 5, 1944, ISSN 0002-9904, S. 284–316, doi:10.1090/S0002-9904-1944-08111-1.
- Gerald Sacks: The recursively enumerable degrees are dense. In: Ann. Of Math.(2). Band 80, Nr. 2, 1964, S. 300–312, doi:10.2307/1970393, JSTOR:1970393.
- Richard A. Shore, Theodore A. Slaman: Defining the Turing jump. In: Mathematical Research Letters. Band 6, 1999, ISSN 1073-2780, S. 711–722.
- Stephen G. Simpson: First-order theory of the degrees of recursive unsolvability. In: Annals of Mathematics. Second Series. Band 105, Nr. 1, 1977, ISSN 0003-486X, S. 121–139, doi:10.2307/1971028, JSTOR:1971028.
- Thomason, S.K.: Sublattices of the recursively enumerable degrees. In: Z. Math. Logik Grundlagen Math. Band 17, 1971, S. 273–280, doi:10.1002/malq.19710170131.
- C.E.M. Yates: A minimal pair of recursively enumerable degrees. In: J. Symbolic Logic. Band 31, Nr. 2, 1966, S. 159–168, doi:10.2307/2269807, JSTOR:2269807.





![{\displaystyle [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fadb3aef0836cb1d004479f470703a45972bf8fe)


![{\displaystyle [X]\leq [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fef5e1a813f5c33d01e1ac65bf5c71a21b50)





![{\displaystyle [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/535e3da41d0b400901796fb059cc7c5b193a4ea0)




![{\displaystyle \left[X^{\prime }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4e881f58e8b4439329a7b152dd482a1a6b64bee)















