Hyperboloid

Ein Hyperboloid ist eine Fläche zweiter Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln, Kreisen geschnitten werden kann.

Es wird zwischen ein- und zweischaligen Hyperboloiden unterschieden, ihr gemeinsamer Grenzfall ist der Doppelkegel.

Hyperboloide werden auch in der synthetischen und der endlichen Geometrie untersucht, dort werden sie als spezielle quadratische Mengen betrachtet.

Einschaliges Hyperboloid

einschaliges Hyperboloid

Das einschalige Hyperboloid gleicht einem Kühlturm, auf der Oberfläche liegen zwei Scharen von Geraden. Daher ist das einschalige Hyperboloid eine Regelfläche. Jede Tangentialebene T schneidet das Hyperboloid in zwei Geraden, deren Schnittpunkt der Berührpunkt von T ist.

Euklidische Normalform: ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1$

Ein einschaliges Hyperboloid mit $a=b$ wird auch als Rotationshyperboloid bezeichnet. Die affine Normalform lautet: $x^{2}+y^{2}-z^{2}=1$.

Das einschalige Hyperboloid ist die einzige nichtausgeartete dreidimensionale Quadrik, die Geraden enthält, ihr Index als quadratische Menge ist 2. Da sich das einschalige Hyperboloid durch „Abrollen“ dieser Geraden erzeugen lässt, zählt es zu den Regelflächen. Für die affine Normalform lassen sich die Geraden so parametrisieren:

$g_{\alpha }:{\vec {x}}={\begin{pmatrix}\cos(\alpha )\\\sin(\alpha )\\0\end{pmatrix}}+t\cdot {\begin{pmatrix}-\sin(\alpha )\\\cos(\alpha )\\1\end{pmatrix}};\quad h_{\alpha }:{\vec {x}}={\begin{pmatrix}\cos(\alpha )\\\sin(\alpha )\\0\end{pmatrix}}+t\cdot {\begin{pmatrix}-\sin(\alpha )\\\cos(\alpha )\\-1\end{pmatrix}}$

Die zwei Scharen $g_{\alpha },h_{\alpha }$ bestehen jeweils aus paarweise windschiefen Geraden. Jede Gerade der einen Schar schneidet im projektiven Abschluss des Raumes jede Gerade der anderen Schar in genau einem Punkt.

Zweischaliges Hyperboloid

zweischaliges Hyperboloid

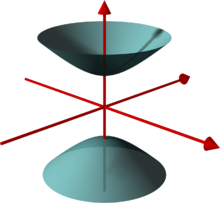
Das zweischalige Hyperboloid besteht aus zwei nicht miteinander verbundenen Teilflächen, es enthält im Gegensatz zum einschaligen Hyperboloid und zum Doppelkegel keine Geraden und ist daher keine Regelfläche.

Euklidische Normalform: ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1$

Die affine Normalform lautet: $x^{2}+y^{2}-z^{2}=-1$.

Doppelkegel

Doppelkegel

Der Grenzfall zwischen ein- und zweischaligen Hyperboloiden, wenn sich die beiden Schalen in einem Punkt berühren, ist der Doppelkegel:

Euklidische Normalform:: ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0$

Die affine Normalform lautet: $x^{2}+y^{2}-z^{2}=0$.

Die im Doppelkegel enthaltenen Geraden lassen sich für die affine Normalform als Schar durch

$g_{\alpha }:{\vec {x}}=t\cdot {\begin{pmatrix}-\sin(\alpha )\\\cos(\alpha )\\1\end{pmatrix}}$

parametrisieren, alle diese Geraden schneiden sich in der Spitze des Doppelkegels.

Symmetrie

Alle Hyperboloide sind

• punktsymmetrisch zu ihrem Mittelpunkt, in der affinen Normalform ist das der Ursprung.
• spiegelsymmetrisch zu genau einer Ebene durch den Mittelpunkt, in der euklidischen Normalform ist das die x-y-Ebene.

Ist in einem Hyperboloid $a=b$, insbesondere in der affinen Normalform, dann ist es

• drehsymmetrisch zu einer Achse a senkrecht zur Symmetrieebene durch den Mittelpunkt, in der Normalform ist das die z-Achse.
• spiegelsymmetrisch zu jeder Ebene durch diese Drehachse.

Parametrisierung

Es gibt verschiedene Möglichkeiten ein Hyperboloid mit einer Funktion $f\colon \mathbb {R} ^{2}\rightarrow \mathbb {R} ^{3}$ zu parametrisieren. Eine einfache Möglichkeit ist die folgende, wobei $d=1$ ein einschaliges, $d=-1$ ein zweischaliges Hyperboloid und $d=0$ einen Doppelkegel liefert:

$f\colon (s,t)\mapsto \left({\begin{array}{lll}a\cdot {\sqrt {s^{2}+d}}\cdot \cos(t)\\b\cdot {\sqrt {s^{2}+d}}\cdot \sin(t)\\c\cdot s\end{array}}\right)$

Weblinks

• Animiertes Hyperboloid bei EXOPAS

Commons: Hyperboloid – Sammlung von Bildern, Videos und Audiodateien

Literatur

• Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X ([http://d-nb.info/972794298/04 [abgerufen am 1. April 2012]). 
• Burkhard Polster: A geometrical picture book. 1. Auflage. Springer, New York/ Berlin/ Heidelberg 1998, ISBN 0-387-98437-2. 
• Hermann Schaal: Lineare Algebra und analytische Geometrie. Band III. Vieweg, 1980, ISBN 3-528-13057-1. 
• Günter Scheja, Uwe Storch: Lehrbuch der Algebra: unter Einschluß der linearen Algebra. 2., überarb. und erw. Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 
• Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik. 2., überarb. und erw. Auflage. BI-Wissenschafts-Verlag, 1999, ISBN 3-411-14101-8. 

Einzelnachweise