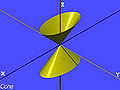
Hyperbel (Mathematik)

In der ebenen Geometrie versteht man unter einer Hyperbel eine spezielle Kurve, die aus zwei zueinander symmetrischen, sich ins Unendliche erstreckenden Ästen besteht. Sie zählt neben dem Kreis, der Parabel und der Ellipse zu den Kegelschnitten, die beim Schnitt einer Ebene mit einem geraden Kreiskegel entstehen.
Wie Ellipse und Parabel lassen sich Hyperbeln als Ortskurven in der Ebene definieren (s. Abschnitt Definition einer Hyperbel als Ortskurve).
Jede Hyperbel lässt sich in einem geeigneten Koordinatensystem durch die Gleichung beschreiben (s. Abschnitt Gleichung).
Die Hyperbel wurde von Menaichmos entdeckt. Die von Apollonios von Perge eingeführte Bezeichnung kommt aus dem Griechischen und bezieht sich auf die Übertreibung (ὑπερβολή hyperbolé, von altgriechisch βάλλειν bállein, deutsch ‚werfen‘, ὑπερβάλλειν hyperballein, deutsch ‚über das Ziel hinaus werfen‘) des Schnittwinkels (oder der numerischen Exzentrizität , s. unten) beim Kegelschnitt: Mit steigendem Schnittwinkel verwandelt sich der Kreis () erst zu immer länglicheren Ellipsen und dann über die Parabel ( und die schneidende Ebene ist parallel zu einer Tangentialebene des Kegels) zu Hyperbeln mit .[1]
Definition einer Hyperbel als Ortskurve[Bearbeiten | Quelltext bearbeiten]

Eine Hyperbel ist definiert als die Menge aller Punkte der Zeichenebene , für die der Betrag der Differenz der Abstände zu zwei gegebenen Punkten, den sogenannten Brennpunkten und , konstant gleich ist:
Der Mittelpunkt der Brennpunkte heißt Mittelpunkt der Hyperbel. Die Verbindungsgerade der Brennpunkte ist die Hauptachse der Hyperbel. Auf der Hauptachse liegen die beiden Scheitel im Abstand vom Mittelpunkt. Der Abstand der Brennpunkte vom Mittelpunkt heißt Brennweite oder lineare Exzentrizität und wird üblicherweise mit bezeichnet. Die in der Einleitung erwähnte dimensionslose numerische Exzentrizität ist .
Dass der Schnitt eines geraden Kreiskegels mit einer Ebene, die steiler ist als die Mantellinien des Kegels und die Kegelspitze nicht enthält, eine Hyperbel ist, zeigt man, indem man die obige definierende Eigenschaft mit Hilfe der Dandelinschen Kugeln nachweist (s. Abschnitt Hyperbel als Kegelschnitt).

Bemerkung:
Die Gleichung lässt sich auch so interpretieren:
Ist der Kreis um mit Radius , so hat vom Kreis denselben Abstand wie vom Brennpunkt : Man nennt den zu gehörigen Leitkreis der Hyperbel. Er erzeugt den rechten Ast
der Hyperbel. Den linken Ast erhält man analog mit dem zum Brennpunkt gehörigen Leitkreis .
Die Erzeugung einer Hyperbel mit Leitkreisen sollte man nicht verwechseln mit der Erzeugung einer Hyperbel mit Leitlinien (siehe unten).
Aufgrund der Leitkreis-Eigenschaft ist ein Ast einer Hyperbel die Äquidistanz-Kurve zu einem ihrer Brennpunkte und dem Leitkreis mit dem anderen Brennpunkt als Mittelpunkt.
Hyperbel in 1. Hauptlage[Bearbeiten | Quelltext bearbeiten]
Gleichung[Bearbeiten | Quelltext bearbeiten]
Die Gleichung der Hyperbel erhält eine besonders einfache Form, wenn sie in 1. Hauptlage liegt, das heißt, dass die beiden Brennpunkte auf der -Achse symmetrisch zum Ursprung liegen; bei einer Hyperbel in 1. Hauptlage haben also die Brennpunkte die Koordinaten und (mit e = lineare Exzentrizität), und die Scheitel haben die Koordinaten und .
Für einen beliebigen Punkt in der Ebene ist der Abstand zum Brennpunkt gleich und zum anderen Brennpunkt . Der Punkt liegt also genau dann auf der Hyperbel, wenn die Differenz dieser beiden Ausdrücke gleich oder gleich ist.
Durch algebraische Umformungen und mit der Abkürzung kann man zeigen, dass die Gleichung
zur Gleichung
äquivalent ist. Letztere Gleichung nennt man die Gleichung der Hyperbel in 1. Hauptlage.
Scheitel[Bearbeiten | Quelltext bearbeiten]
Eine Hyperbel besitzt nur zwei Scheitel: und . Im Gegensatz zur Ellipse sind hier und keine Kurvenpunkte. Letztere werden deswegen auch imaginäre Nebenscheitel genannt. Die Gerade durch die Nebenscheitel heißt Nebenachse. Die Hyperbel liegt symmetrisch zur Haupt- und Nebenachse.
Asymptoten[Bearbeiten | Quelltext bearbeiten]

Löst man die Hyperbelgleichung nach auf, so erhält man
Hier erkennt man, dass sich die Hyperbel für betragsmäßig große an die Geraden
beliebig dicht annähert. Diese Geraden gehen durch den Mittelpunkt und heißen die Asymptoten der Hyperbel
Der Winkel zwischen den Asymptoten (der den Brennpunkt einschließt) beträgt
- .
Halbparameter p[Bearbeiten | Quelltext bearbeiten]
Die halbe Länge einer Hyperbelsehne, die durch einen Brennpunkt geht und zur Hauptachse senkrecht verläuft, nennt man den Halbparameter (manchmal auch Quermaß oder nur Parameter) der Hyperbel. Er lässt sich berechnen durch
Weitere Bedeutung von :
- ist der Scheitelkrümmungskreisradius,
d. h., ist der Radius desjenigen Kreises durch einen Scheitel, der sich an die Hyperbel im Scheitel am besten anschmiegt. (Siehe unten: Formelsammlung/Scheitelgleichung.)
Tangente[Bearbeiten | Quelltext bearbeiten]
Die Gleichung der Tangente in einem Hyperbelpunkt findet man am einfachsten durch implizites Differenzieren der Hyperbelgleichung :
Unter Berücksichtigung von ergibt sich:
Gleichseitige Hyperbel[Bearbeiten | Quelltext bearbeiten]
Eine Hyperbel, für die gilt, heißt gleichseitige Hyperbel. Ihre Asymptoten stehen senkrecht aufeinander. Die lineare Exzentrizität ist , die numerische Exzentrizität und der Halbparameter ist .
Parameterdarstellung mit Hyperbelfunktionen[Bearbeiten | Quelltext bearbeiten]
Mit den Hyperbelfunktionen ergibt sich eine (zur Ellipse analoge) Parameterdarstellung der Hyperbel :
Hyperbel in 2. Hauptlage[Bearbeiten | Quelltext bearbeiten]
Vertauscht man und , so erhält man Hyperbeln in 2. Hauptlage:
Hyperbel mit einer Gleichung y=A/x[Bearbeiten | Quelltext bearbeiten]


rot: A=1, magenta: A=4; blau: A=9
Dreht man das x-y-Koordinatensystem um den Winkel und nennt die neuen Koordinaten , so ist .
Die gleichseitige Hyperbel (die Halbachsen sind gleich lang!) hat in den neuen Koordinaten die Gleichung .
Löst man diese Gleichung nach auf, erhält man
Also ist (in einem x-y-Koordinatensystem) der Graph der Funktion mit der Gleichung
- eine gleichseitige Hyperbel mit
- den Koordinatenachsen als Asymptoten,
- der Gerade als Hauptachse,
- dem Mittelpunkt und den Halbachsen
- den Scheiteln
- dem Halbparameter und Scheitelkrümmungskreisradius
- der linearen Exzentrizität und der numerischen Exzentrizität
- der Tangente im Punkt
Dreht man die ursprüngliche Hyperbel um (dies entspricht einer Drehung des Koordinatensystems um ), so erhält man eine gleichseitige Hyperbel mit der Gleichung
- mit
- den Halbachsen
- der Gerade als Hauptachse,
- den Scheiteln
Verschiebt man die Hyperbel mit der Gleichung so, dass der Punkt der Mittelpunkt der verschobenen Hyperbel ist, so hat die verschobene Hyperbel die Gleichung
Die verschobene Hyperbel hat die Asymptoten und .
Die Parameter ändern sich bei einer Verschiebung nicht.
Hyperbel als Kegelschnitt[Bearbeiten | Quelltext bearbeiten]

Schneidet man einen geraden Kreiskegel mit einer Ebene , deren Neigung größer als die Neigung der Mantellinien des Kegels ist und die nicht durch die Kegelspitze geht, so ergibt sich eine Hyperbel als Schnittkurve (s. Bild, rote Kurve). Den Nachweis der definierenden Eigenschaft bzgl. der Brennpunkte (s. oben) führt man mit Hilfe zweier Dandelinscher Kugeln , das sind Kugeln, die den Kegel in Kreisen bzw. und die Hyperbelebene in Punkten bzw. berühren. Es stellt sich heraus, dass die Brennpunkte der Schnitthyperbel sind.
- sei ein beliebiger Punkt der Schnittkurve.
- Die Mantellinie durch schneidet den Kreis in einem Punkt und den Kreis in einem Punkt .
- Die Strecken und sind tangential zur Kugel und damit gleich lang.
- Die Strecken und sind tangential zur Kugel und damit auch gleich lang.
- Also ist und damit unabhängig vom Hyperbelpunkt .
Tangente als Winkelhalbierende[Bearbeiten | Quelltext bearbeiten]

Für eine Hyperbel gilt:
- Die Tangente in einem Punkt ist die Winkelhalbierende der Brennstrahlen
Daraus folgt: Ein Lichtstrahl, der von einem Brennpunkt ausgeht, wird demnach an der Hyperbeltangente so reflektiert, dass er vom anderen Brennpunkt auszugehen scheint.
- Beweis
Zum Beweis verwendet man den Hilfspunkt auf dem Brennstrahl , der von den Abstand hat (s. Bild, ist die Halbachse der Hyperbel). Die Gerade ist die Winkelhalbierende der Brennstrahlen. Um nachzuweisen, dass die Tangente im Punkt ist, zeigt man, dass jeder von verschiedene Punkt von nicht auf der Hyperbel liegen kann. Also kann die Hyperbel nur im Punkt schneiden und ist damit die Tangente in . Aus der Zeichnung ist ersichtlich (Dreiecksungleichung), dass ist, d. h., es ist . Wenn ein Hyperbelpunkt wäre, müsste die Differenz gleich sein.
Da eine Winkelhalbierende leicht zu zeichnen ist, bietet diese Eigenschaft eine einfache Möglichkeit die Tangente in einem Hyperbelpunkt zu konstruieren. Falls statt der zwei Brennpunkte die zwei Asymptoten bekannt sind, kann man die im Abschnitt Tangentenkonstruktion beschriebene Methode verwenden.
Leitlinien-Eigenschaft[Bearbeiten | Quelltext bearbeiten]

Mit dem Begriff Direktrix oder Leitlinie bezeichnet man die beiden Parallelen zur Nebenachse im Abstand . Für einen beliebigen Punkt der Hyperbel ist das Verhältnis zwischen den Abständen zu einem Brennpunkt und zur zugehörigen Leitlinie gleich der numerischen Exzentrizität:
Zum Beweis zeigt man, dass für und die Gleichung
erfüllt ist.
Umgekehrt kann man einen Punkt (als Brennpunkt) und eine Gerade (als Leitlinie) sowie eine reelle Zahl mit vorgeben und eine Hyperbel definieren als
- Menge aller Punkte der Ebene, für die das Verhältnis der Abstände zu dem Punkt und zu der Geraden gleich ist.
Wählt man , so erhält man eine Parabel. Für ergibt sich eine Ellipse.
Zum Beweis geht man von und der Vorgabe, dass ein Kurvenpunkt ist, aus. Die Leitlinie wird dann durch die Gleichung beschrieben. Für folgt aus
- und hieraus
Mit der Abkürzung erhält man
Dies ist die Scheitelgleichung einer Ellipse (), einer Parabel () oder einer Hyperbel (). Siehe Abschnitt Formelsammlung.
Führt man im Fall neue Konstanten so ein, dass ist, so geht die Scheitelgleichung in
über. Dies ist die Gleichung einer Hyperbel mit Mittelpunkt , -Achse als Hauptachse und Halbachsen .
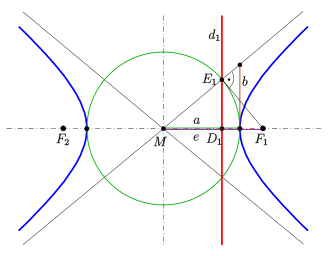
Konstruktion einer Leitlinie:
Wegen sind der Punkt der Leitlinie (siehe Bild) und der Brennpunkt bezüglich der Spiegelung am großen Scheitelkreis (im Bild grün) invers. Damit kann wie im Bild gezeigt aus mit Hilfe des großen Scheitelkreises konstruiert werden: Der Punkt ist der Schnittpunkt des Scheitelkreises mit dem Thaleskreis (hier nicht gezeichnet) über . Man rechnet nach, dass auch auf der Asymptote liegt. Damit gibt es die weitere Konstruktion von als Lotfußpunkt des Lotes von auf die Asymptote (siehe Bild). Die Leitlinie ist schließlich das Lot von auf die große Achse.
Fadenkonstruktion einer Hyperbel[Bearbeiten | Quelltext bearbeiten]
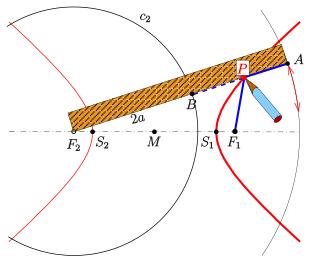
Die Definition einer Hyperbel mit Hilfe eines Leitkreises (s. o.) bietet eine einfache Möglichkeit, mit Hilfe eines Fadens und eines Lineals einen Hyperbelbogen zu zeichnen:[2]
(0) Wahl der Brennpunkte und des Abstandes der Scheitel; der Radius des Leitkreises ist auch
(1) Das Lineal wird mit einem Ende im linken Brennpunkt drehbar befestigt und der Punkt im Abstand an der Kante markiert
(2) Faden (blau) der Länge
(3) Befestigung des einen Fadenendes im Punkt des Lineals, das andere Ende im Brennpunkt
(4) Mit einem Stift den Faden so spannen, dass er an der Linealkante anliegt
(5) Durch Drehen des Lineals um den Punkt überstreicht der Stift einen Hyperbelbogen, denn es ist (Leitkreiseigenschaft).
Steiner-Erzeugung einer Hyperbel[Bearbeiten | Quelltext bearbeiten]
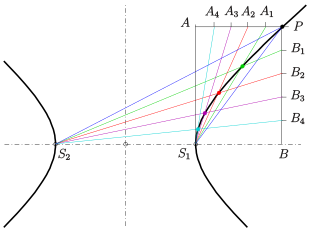

Die folgende Idee, einzelne Punkte einer Hyperbel zu konstruieren, beruht auf der Steiner-Erzeugung eines Kegelschnitts (nach dem Schweizer Mathematiker Jakob Steiner):
- Hat man für zwei Geradenbüschel in zwei Punkten (alle Geraden durch den Punkt bzw. ) eine projektive, aber nicht perspektive Abbildung des einen Büschels auf das andere, so bilden die Schnittpunkte zugeordneter Geraden einen nichtausgearteten Kegelschnitt.[3][4]
Für die Erzeugung einzelner Punkte der Hyperbel gehen wir von den Geradenbüscheln in den Scheiteln aus. Seien nun ein Punkt der Hyperbel und . Wir unterteilen die Rechteckseite in n gleiche Stücke und übertragen diese Unterteilung mittels einer Parallelprojektion in Richtung der Diagonalen auf die Strecke (s. Bild). Die benutzte Parallelprojektion vermittelt die nötige projektive Abbildung der Büschel in und . Die Schnittpunkte der zugeordneten Geraden und liegen dann auf der durch die Vorgaben eindeutig bestimmten Hyperbel.
Bemerkung: Die Unterteilungen lassen sich jenseits der Punkte bzw. fortsetzen, um weitere Punkte zu konstruieren. Da aber dann schleifende Schnitte und eine sehr ungleiche Punkteverteilung auftreten, ist es besser, die Konstruktion der obigen Punkte symmetrisch auf die anderen Hyperbelteile zu übertragen (s. Animation).
Bemerkung:
- Auch für Ellipsen und Parabeln gibt es die Steiner-Erzeugung. Im Parabelfall lässt sich die Behauptung leicht nachrechnen.
- Die Steiner-Erzeugung wird auch Parallelogramm-Methode genannt, da man statt der Scheitel auch andere Hyperbelpunkte auf einem Hyperbeldurchmesser verwenden kann. Dann tritt ein Parallelogramm statt eines Rechtecks auf.
Hyperbel als affines Bild der Einheitshyperbel[Bearbeiten | Quelltext bearbeiten]

Eine andere Definition der Hyperbel benutzt eine spezielle geometrische Abbildung, nämlich die Affinität. Hier ist die Hyperbel als affines Bild der Einheitshyperbel definiert.
- Parameterdarstellung
Eine affine Abbildung in der reellen Ebene hat die Form , wobei eine reguläre Matrix (Determinante nicht 0) und ein beliebiger Vektor ist. Sind die Spaltenvektoren der Matrix , so wird die Einheitshyperbel auf die Hyperbel
abgebildet. ist der Mittelpunkt, ein Punkt der Hyperbel und Tangentenvektor in diesem Punkt. stehen i. a. nicht senkrecht aufeinander. D. h. sind i. A. nicht die Scheitel der Hyperbel. Aber sind die Richtungsvektoren der Asymptoten. Diese Definition einer Hyperbel liefert eine einfache Parameterdarstellung einer beliebigen Hyperbel.
- Scheitel, Scheitelform
Da in einem Scheitel die Tangente zum zugehörigen Hyperbeldurchmesser senkrecht steht und die Tangentenrichtung in einem Hyperbelpunkt
ist, ergibt sich der Parameter eines Scheitels aus der Gleichung
und damit aus
zu
Es wurden die Formeln benutzt.
Falls ist, ist und die Parameterdarstellung schon in Scheitelform.
Die zwei Scheitel der Hyperbel sind
Aus
und den Additionstheoremen für die Hyperbelfunktionen ergibt sich die Scheitelform der Parameterdarstellung der Hyperbel:
- Beispiele


- liefert die übliche Parameterdarstellung der Hyperbel mit der Gleichung
- liefert die Parameterdarstellung der Hyperbel, die aus der Hyperbel durch Drehung um den Winkel und anschließende Verschiebung um hervorgeht. Die Parameterdarstellung ist schon in Scheitelform. D. h., sind die Scheitel der Hyperbel.
- liefert die Hyperbel mit der Gleichung Beim Nachweis von verwende man
- Bildet man die Hyperbel mit affinen Abbildungen der Form ab, so erhält man die Schar aller Hyperbeln mit achsenparallelen Asymptoten. Der Mittelpunkt solch einer Hyperbel ist Die Besonderheit dieser Hyperbelschar ist, dass sie sich als Funktionsgraphen darstellen lassen.
- Die Parameterdarstellung
- einer Hyperbel ist nicht in Scheitelform.
- Der Scheitelparameter ergibt sich aus zu
- Die Scheitelform der Parameterdarstellung ist:
- Die Scheitel sind und
- die Halbachsen
- implizite Darstellung
Löst man die Parameterdarstellung mit Hilfe der Cramerschen Regel nach auf und verwendet , erhält man die implizite Darstellung
- .
- Hyperbel im Raum
Sind die Vektoren aus dem , so erhält man eine Parameterdarstellung einer Hyperbel im Raum.
Hyperbel als affines Bild der Hyperbel y=1/x[Bearbeiten | Quelltext bearbeiten]
Da die Einheitshyperbel zur Hyperbel äquivalent ist (s. o.), kann man eine beliebige Hyperbel auch als affines Bild der Hyperbel auffassen:
ist der Mittelpunkt der Hyperbel, zeigen in Richtung der Asymptoten und ist ein Punkt der Hyperbel.
Für den Tangentenvektor ergibt sich
In einem Scheitel steht die Tangente zum zugehörigen Hyperbeldurchmesser senkrecht, d. h., es ist
Also ist der Scheitelparameter
Für ist und sind die Scheitel der Hyperbel.
Tangentenkonstruktion[Bearbeiten | Quelltext bearbeiten]

Der Tangentenvektor kann durch Ausklammern von so geschrieben werden:
D. h., in dem Parallelogramm ist die Diagonale parallel zur Tangente im Hyperbelpunkt (s. Bild). Diese Eigenschaft bietet eine einfache Möglichkeit, die Tangente in einem Hyperbelpunkt zu konstruieren.
Bemerkung: Diese Eigenschaft einer Hyperbel ist eine affine Version der 3-Punkte-Ausartung des Satzes von Pascal.[5]
Punktkonstruktion[Bearbeiten | Quelltext bearbeiten]

Eine weitere Eigenschaft einer Hyperbel erlaubt die Konstruktion von Hyperbelpunkten, falls die Asymptoten und ein Punkt der Hyperbel bekannt sind:
Für eine Hyperbel mit der Parameterdarstellung (der Mittelpunkt wurde der Einfachheit halber als Nullpunkt angenommen) gilt:
Sind zwei Hyperbelpunkte, so liegen die Punkte
auf einer Geraden durch den Mittelpunkt (s. Bild). Der einfache Beweis ergibt sich aus .
Bemerkung: Diese Eigenschaft einer Hyperbel ist eine affine Version der 4-Punkte-Ausartung des Satzes von Pascal.[6]
Tangenten-Asymptoten-Dreieck[Bearbeiten | Quelltext bearbeiten]

Für die folgenden Überlegungen, nehmen wir der Einfachheit halber an, dass der Mittelpunkt sich im Nullpunkt (0,0) befindet und dass die Vektoren die gleiche Länge haben. Falls Letzteres nicht der Fall sein sollte, wird die Parameterdarstellung zuerst in Scheitelform gebracht (s. o.). Dies hat zur Folge, dass die Scheitel und die Nebenscheitel sind. Also ist und .
Berechnet man die Schnittpunkte der Tangente in dem Hyperbelpunkt mit den Asymptoten, so erhält man die beiden Punkte
Der Flächeninhalt des Dreiecks lässt sich mit Hilfe einer 2×2-Determinante ausdrücken:
S. Rechenregeln für Determinanten. ist der Flächeninhalt der von aufgespannten Raute. Der Flächeninhalt einer Raute ist gleich der Hälfte des Diagonalenproduktes. Die Diagonalen dieser Raute sind die Halbachsen . Also gilt:
- Der Flächeninhalt des Dreiecks ist unabhängig vom Hyperbelpunkt
Affine Selbstabbildungen der Hyperbel y=1/x[Bearbeiten | Quelltext bearbeiten]
Nicht jede affine Abbildung der reellen affinen Ebene (s. vorigen Abschnitt) bildet die Hyperbel auf eine andere Hyperbel ab. Die folgenden affinen Abbildungen lassen die Hyperbel als Ganzes invariant:
Spezialfälle:
- Für bleibt jeder Punkt der Ebene fest. Diese Abbildung heißt Identität.
- Für wird jeder Punkt der Hyperbel bewegt, d. h., es gibt keinen Fixpunkt auf der Hyperbel.
- Für ist die Abbildung die Punktspiegelung am Nullpunkt.
- Für ist die Abbildung die „normale“ Spiegelung an der Geraden .
- Für ist die Abbildung die Schrägspiegelung an der Gerade in Richtung der Geraden . (Siehe Abschnitt Mittelpunkte paralleler Sehnen.)
Mittelpunkte paralleler Sehnen[Bearbeiten | Quelltext bearbeiten]


Für jede Hyperbel gilt:
- Die Mittelpunkte paralleler Sehnen (s. Bild) liegen auf einer Geraden durch den Mittelpunkt der Hyperbel.
D. h., zu jedem Punktepaar einer Sehne gibt es eine Schrägspiegelung an einer Geraden durch den Mittelpunkt der Hyperbel, die die Punkte vertauscht und die Hyperbel auf sich abbildet. Dabei versteht man unter einer Schrägspiegelung eine Verallgemeinerung einer gewöhnlichen Spiegelung an einer Geraden , bei der alle Strecken Punkt–Bildpunkt zwar zueinander parallel, aber nicht unbedingt senkrecht zur Spiegelachse sind.
Den Nachweis dieser Eigenschaft führt man am einfachsten an der Hyperbel durch. Da alle Hyperbeln affine Bilder der Einheitshyperbel und damit auch von der Hyperbel sind und bei einer affinen Abbildung Mittelpunkte von Strecken in die Mittelpunkte der Bildstrecken übergehen, gilt die obige Eigenschaft für alle Hyperbeln.
Bemerkung: Die Punkte der Sehne dürfen auch auf verschiedenen Ästen der Hyperbel liegen.
Eine Folgerung dieser Symmetrie ist: Die Asymptoten der Hyperbel werden bei der Schrägspiegelung vertauscht und der Mittelpunkt einer Hyperbelsehne halbiert auch die zugehörige Strecke zwischen den Asymptoten, d. h., es gilt . Diese Eigenschaft kann man benutzen, um bei bekannten Asymptoten und einem Punkt beliebig viele weitere Hyperbelpunkte zu konstruieren, indem man die jeweilige Strecke zur Konstruktion von verwendet.
Entartet die Sehne zu einer Tangente, so halbiert der Berührpunkt den Abschnitt zwischen den Asymptoten.
Pol-Polare-Beziehung[Bearbeiten | Quelltext bearbeiten]
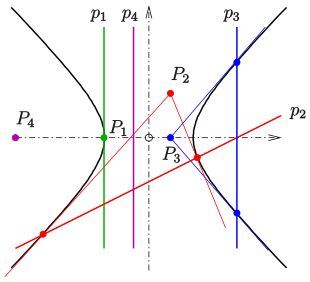
Eine Hyperbel lässt sich in einem geeigneten Koordinatensystem immer durch eine Gleichung der Form beschreiben. Die Gleichung der Tangente in einem Hyperbelpunkt ist Lässt man in dieser Gleichung zu, dass ein beliebiger vom Nullpunkt verschiedener Punkt der Ebene ist, so wird dem Punkt die Gerade zugeordnet. Diese Gerade geht nicht durch den Mittelpunkt der Hyperbel.
Umgekehrt kann man
- der Geraden den Punkt bzw.
- der Geraden den Punkt
zuordnen. Solch eine Zuordnung Punkt ↔ Gerade nennt man eine Polarität oder Pol-Polare-Beziehung. Der Pol ist der Punkt, die Polare ist die zugehörige Gerade.
Die Bedeutung dieser Pol-Polare-Beziehung besteht darin, dass die möglichen Schnittpunkte der Polare eines Punktes mit der Hyperbel die Berührpunkte der Tangenten durch den Pol an die Hyperbel sind.
- Liegt der Punkt (Pol) auf der Hyperbel, so ist seine Polare die Tangente in diesem Punkt (s. Bild: ).
- Liegt der Pol außerhalb der Hyperbel, so sind die Schnittpunkte der Polare mit der Hyperbel die Berührpunkte der Tangenten durch den Pol an die Hyperbel (s. Bild: ).
- Liegt der Punkt innerhalb der Hyperbel, so hat seine Polare keinen Schnittpunkt mit der Hyperbel (s. Bild: ).
Zum Beweis: Die Bestimmung der Schnittpunkte der Polare eines Punktes mit der Hyperbel und die Suche nach Hyperbelpunkten, deren Tangenten den Punkt enthalten, führen auf dasselbe Gleichungssystem.
Bemerkungen:
- Der Schnittpunkt zweier Polaren (z. B. im Bild: ) ist der Pol der Verbindungsgeraden der zugehörigen Pole (hier: ).
- Der Brennpunkt bzw. und die Leitlinie bzw. sind zueinander polar.
- Geraden durch den Mittelpunkt der Hyperbel haben keine Pole. Man sagt: „Ihre Pole liegen auf der Ferngeraden.“
- Der Mittelpunkt der Hyperbel hat keine Polare, „sie ist die Ferngerade“.
- Pol-Polare-Beziehungen gibt es auch für Ellipsen und Parabeln. Siehe auch projektiver Kegelschnitt.
Orthogonale Tangenten[Bearbeiten | Quelltext bearbeiten]

Für eine Hyperbel liegen die Schnittpunkte orthogonaler Tangenten auf dem Kreis . (Im Fall gibt es keine orthogonalen Tangenten.)
Diesen Kreis nennt man die orthoptische Kurve der gegebenen Hyperbel.
Hyperbeln der Form y=a/(x−b)+c[Bearbeiten | Quelltext bearbeiten]
Peripheriewinkelsatz für Hyperbeln[Bearbeiten | Quelltext bearbeiten]
Hyperbeln der Form sind Funktionsgraphen, die durch die drei Parameter eindeutig bestimmt sind. Man benötigt also drei Punkte, um diese Parameter zu ermitteln. Eine schnelle Methode beruht auf dem Peripheriewinkelsatz für Hyperbeln.

Um einen Winkel zwischen zwei Sehnen zu messen, führen wir für zwei Geraden, die weder zur - noch zur -Achse parallel sind, ein Winkelmaß ein:
- Für zwei Geraden messen wir den zugehörigen Winkel mit der Zahl .
Zwei Geraden sind parallel, wenn und damit das Winkelmaß gleich 1 ist.
Analog zum Peripheriewinkelsatz für Kreise gilt hier der
Peripheriewinkelsatz (für Hyperbeln):
- Für vier Punkte (s. Bild) gilt:
- Die vier Punkte liegen nur dann auf einer Hyperbel der Form , wenn die Winkel bei und im obigen Winkelmaß gleich sind, d. h., wenn:
(Beweis durch Nachrechnen. Dabei kann man für die eine Richtung voraussetzen, dass die Punkte auf einer Hyperbel y=a/x liegen.)
3-Punkte-Form einer Hyperbel[Bearbeiten | Quelltext bearbeiten]
Analog zur 2-Punkte-Form einer Geraden (Steigungswinkel werden mit der Steigung gemessen) folgt aus dem Peripheriewinkelsatz für Hyperbeln die
3-Punkte-Form (für Hyperbeln):
- Die Gleichung der Hyperbel durch drei Punkte ergibt sich durch Auflösen der Gleichung
- nach y.
Formelsammlung[Bearbeiten | Quelltext bearbeiten]
Hyperbelgleichung[Bearbeiten | Quelltext bearbeiten]
Eine Hyperbel mit Mittelpunkt (0|0) und -Achse als Hauptachse erfüllt die Gleichung
Die Asymptoten der zugehörigen Hyperbel sind die Geraden:
Brennpunkte sind:
Eine Hyperbel mit Mittelpunkt und der Geraden als Hauptachse erfüllt die Gleichung
Eine beliebige Hyperbel, deren Asymptoten die Geraden mit den Gleichungen sind, besitzt eine Gleichung der Form
Z. B.: Sind die Asymptoten die Koordinatenachsen , ergeben sich alle Hyperbeln mit einer Gleichung .
Scheitelgleichung[Bearbeiten | Quelltext bearbeiten]
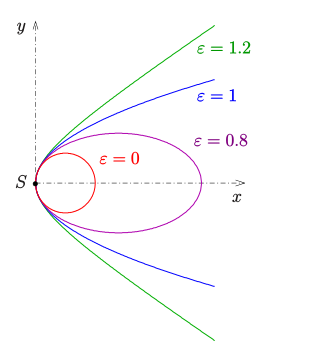
Die Schar der Hyperbeln, deren Achse die -Achse, ein Scheitel der Punkt (0,0) und der Mittelpunkt (–a,0) ist, lässt sich durch die Gleichung
beschreiben.
Für Hyperbeln gilt . Setzt man in dieser Gleichung
- , so erhält man einen Kreis,
- für eine Ellipse,
- für eine Parabel.
Die Kegelschnitte haben bei gleichem Halbparameter alle denselben Krümmungskreisradius im Scheitel S:
Parameterdarstellungen[Bearbeiten | Quelltext bearbeiten]
für die Hyperbel mit der Gleichung :
1:
2:
3: (Darstellung mit rationalen Funktionen).
4: Tangentensteigung als Parameter:
Eine Parameterdarstellung, die die Tangentensteigung in dem jeweiligen Hyperbelpunkt verwendet, erhält man analog zum Fall der Ellipse, indem man dort durch ersetzt und Formeln für die hyperbolischen Funktionen verwendet:
Hierbei ist die obere und die untere Hälfte der Hyperbel. Die Punkte mit senkrechten Tangenten (Scheitel ) werden durch diese Parameterdarstellung nicht erfasst.
Die Gleichung der Tangente im Punkt ist
Diese Gleichung ist ein wesentliches Hilfsmittel bei der Bestimmung der orthoptischen Kurve einer Hyperbel.
In Polarkoordinaten[Bearbeiten | Quelltext bearbeiten]
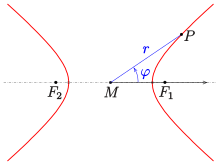

Man beachte
- im ersten Fall (Pol ist der Mittelpunkt der Hyperbel), dass der Radikand negativ werden kann. Für solche Winkel ergeben sich keine Hyperbelpunkte.
- Im zweiten Fall (Pol ist ein Brennpunkt der Hyperbel) liegen auf jedem Strahl, für den der Nenner nicht 0 ist, zwei Hyperbelpunkte (wegen ). Für ergeben sich die beiden Scheitel.
Winkel zur Hauptachse, Pol im Mittelpunkt (0,0):
Winkel zur Hauptachse, Pol in einem Brennpunkt (s. Kegelschnitt):
Tangentengleichung[Bearbeiten | Quelltext bearbeiten]
Mittelpunkt (0|0), Hauptachse als -Achse, Berührpunkt
Mittelpunkt , Hauptachse parallel zur -Achse, Berührpunkt
Krümmungskreisradius[Bearbeiten | Quelltext bearbeiten]
Der Krümmungskreisradius der Hyperbel in den beiden Scheiteln ist
- (wie bei einer Ellipse in den Hauptscheiteln).
Hyperbel als Trisektrix[Bearbeiten | Quelltext bearbeiten]
Bereits Pappos von Alexandria nutzte im 4. Jahrhundert für seine Lösung des Problems Dreiteilung eines Winkels diese Eigenschaft der Hyperbel als zusätzliches Hilfsmittel.[7][8] Erwiesenermaßen gibt es bei Beschränkung auf die „euklidischen Werkzeuge“ Zirkel und Lineal keine Lösung.
Die im Folgenden beschriebene Methode ist weitgehend dem Aufsatz Zur Trisektion des Winkels von K. Matter (1902) entnommen.[9] In der darin gezeigten Konstruktion liegt der Winkelscheitel im Gegensatz zu der nach Pappos,[7] nicht auf der Ordinate der Hyperbel. Nimmt man für unterschiedliche Winkelweiten stets die gleiche Sehnenlänge so können mit nur einer konstruierten Hyperbel die Winkelweiten ab ca. bis bei genügenden Platzverhältnissen bereits ab nahe gedrittelt werden. Die Bezeichnungen der Hyperbel wurden dem derzeit üblichen Stand angepasst.

Als Vorüberlegung stellt man sich z. B. einen Winkel als Teil eines Kreissektors vor, in dem der Punkt den Kreisbogen im Verhältnis teilt. Ein darin eingezeichnetes Dreieck mit der Sehne erhält somit gemäß Kreiswinkelsatz am Scheitel den Winkel und am Scheitel den Winkel Ist der Scheitel der Koordinatenursprung des kartesischen Koordinatensystems, gilt für den Punkt die -Koordinate (Strecke )
- (1)
Elimination des
- Terme der Gleichung (1) umformen
- (2)
- (3) ist eine Doppelwinkelfunktion, deshalb gilt auch
- (4)
- (2) einsetzen in (4)
- (5)
- (5) und (3) gleichsetzen, quasi eliminieren
- (6)
- somit gilt für
- (7)
schließlich bekommt man die Hyperbelgleichung
Daraus ergeben sich konstruktionsrelevante Merkmale, die auch ohne Verwendung des kartesischen Koordinatensystems gelten, d. h. eine bestimmte Richtung oder Position der Sehne ist nicht erforderlich:
- der Mittelpunkt liegt auf der Sehne
- die Halbachse
- die Exzentrizität
- der linke Hyperbelast verläuft durch den Scheitel (im Weiteren mit Scheitel bezeichnet).

Die eigentliche Konstruktion beginnt mit dem Positionieren des Winkelscheitels und dem Einzeichnen der beiden Winkelschenkel, die eine beliebige Winkelweite des Winkels einschließen. Anschließend wird ein Kreisbogen um mit frei wählbarem Radius gezogen; dabei ergeben sich an den Winkelschenkeln der erste Brennpunkt und der zweite Scheitel der späteren Hyperbel. Es folgt eine Gerade durch die Punkte und Die Strecke ist quasi die Sehne Nach dem Dritteln der Sehne in und wird die Strecke ab auf die Gerade abgetragen, daraus ergeben sich für die gesuchte Hyperbel der zweite Brennpunkt sowie die
- Halbachse und die
- Exzentrizität
Nun wird die Hyperbel mithilfe der Brennpunkte des Scheitelpunktes sowie z. B. mittels einer Dynamische-Geometrie-Software (DGS) oder einem mechanischen Hyperbelzirkel eingezeichnet.
Der rechte Hyperbelast schneidet in den Kreisbogen und liefert den Abschließend bedarf es nur noch einer Halbgeraden ab durch
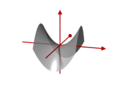
Hyperbeln als ebene Schnitte von Quadriken[Bearbeiten | Quelltext bearbeiten]
Folgende Flächen zweiter Ordnung (Quadriken) besitzen Hyperbeln als ebene Schnitte:
- Elliptischer Kegel[10] (siehe auch Kegelschnitt)
- Hyperbolischer Zylinder
- Hyperbolisches Paraboloid
- Einschaliges Hyperboloid[11]
- Zweischaliges Hyperboloid[12]
-
Elliptischer Kegel
-
Hyperbolischer Zylinder
-
Hyperbolisches Paraboloid
-
Einschaliges Hyperboloid
-
Zweischaliges Hyperboloid
Hyperbel y=1/x über einem beliebigen Zahlkörper[Bearbeiten | Quelltext bearbeiten]
Betrachtet man in einer affinen Ebene über einem beliebigen (kommutativen) Körper die Punktmenge, die der Hyperbelgleichung genügt, so bleiben viele Eigenschaften des reellen Falls, die mit „schneiden“, „verbinden“ und „parallel“ formuliert werden und deren Beweise nur Multiplikation/Division und Addition/Subtraktion verwenden, erhalten.[3] Z. B.:
- Eine Gerade schneidet die Hyperbel in höchstens zwei Punkten.
- Durch jeden Hyperbelpunkt gibt es außer den achsenparallelen Geraden genau eine Gerade, die mit der Hyperbel nur den Punkt gemeinsam hat, die Tangente: . Eine Gerade ohne Schnittpunkt heißt Passante, eine mit zwei Schnittpunkten Sekante.
Unterschiede zum reellen Fall:
- Für (rationale Zahlen) ist die Gerade eine Passante, denn die Gleichung hat in keine Lösung.
- Für (komplexe Zahlen) gibt es keine Passanten. Z. B.: schneidet die Hyperbel in den Punkten .
- Hat der Körper die Charakteristik 2 (d. h., es gilt 1 + 1 = 0), so gibt es unter den Geraden keine Sekanten, da jede Gleichung im Fall Charakteristik 2 höchstens eine Lösung hat (es gibt kein „“). Die Tangente im Hyperbelpunkt hat (bei Charakteristik 2) die Gleichung . D. h., alle Tangenten gehen durch den Nullpunkt (0,0).
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Vorkommen[Bearbeiten | Quelltext bearbeiten]
-
Skulptur Mae West in Form eines einschaligen Hyperboloids auf dem Effnerplatz in München
-
Architektur: Kathedrale von Brasilia
-
Sonnenuhr: Weg der Schattenspitze im Tagesverlauf
-
Lichtkegel an einer Wand
Literatur[Bearbeiten | Quelltext bearbeiten]
- Peter Proff: Die Deutung der Begriffe „Ellipse“, „Parabel“ und „Hyperbel“ nach Apollonios v. Perge. In: „gelêrter der arzeniê, ouch apotêker“. Beiträge zur Wissenschaftsgeschichte. Festschrift zum 70. Geburtstag von Willem F. Daems. Hrsg. von Gundolf Keil, Horst Wellm Verlag, Pattensen/Hannover 1982 (= Würzburger medizinhistorische Forschungen, 24), ISBN 3-921456-35-5, S. 17–34.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Hyperbola. In: MathWorld (englisch).
- Fadenkonstruktion einer Hyperbel. Geogebra
- John J. O’Connor, Edmund F. Robertson: Hyperbola. In: MacTutor History of Mathematics archive (englisch).
- Berechnungen zu Hyperbeln (JavaScript)
- Hyperbel. In: mathematische-basteleien.de. Abgerufen am 9. Februar 2015.
- Frans van Schooten: Mathematische Oeffeningen. 1659
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ I. N. Bronstein, K. A. Semendjajew (Begründer), Günter Grosche (Bearb.), Eberhard Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6, S. 24.
- ↑ Frans van Schooten: Mathematische Oeffeningen, Leyden, 1659, S. 327
- ↑ a b Erich Hartmann: Projektive Geometrie. (PDF; 180 kB). Kurzskript, TU Darmstadt, S. 12–16.
- ↑ Jacob Steiner’s Vorlesungen über synthetische Geometrie. B. G. Teubner, Leipzig 1867. 2. Teil, S. 96. (eingeschränkte Vorschau in der Google-Buchsuche)
- ↑ Lecture Note Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 870 kB) S. 33.
- ↑ Lecture Note Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 870 kB) S. 32.
- ↑ a b Regina Bruischütz: 5. Winkeldreiteilung mit Hyperbeln (nach Pappus ca. 300 n. Chr.). In: Winkeldreiteilung - Konstruktion mit zusätzlichen Hilfsmitteln (Teil A). Universität Bayreuth, 26. Mai 1997, S. 3, archiviert vom ; abgerufen am 10. Mai 2022.
- ↑ Robert C. Yates: THE TRISECTION PROBLEM, 3. The Hyperbola. In: ERIC. National Council of Teachers of Mathematics, Inc., Washington, D.C., 1971, S. 32–33, abgerufen am 27. Juli 2019.
- ↑ K. Matter: Zur Trisektion des Winkels. In: e-perodica. ETH zürich, 1902, S. 20–23, abgerufen am 22. Juli 2019.
- ↑ CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. (PDF; 3,4 MB) TU Darmstadt, S. 108.
- ↑ CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. (PDF; 3,4 MB) TU Darmstadt, S. 118.
- ↑ CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. (PDF; 3,4 MB) TU Darmstadt, S. 123.

























































































































































































![{\displaystyle t_{0}=\pm {\sqrt[{4}]{\frac {{\vec {f}}_{2}^{2}}{{\vec {f}}_{1}^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b26de698fecd55664d5a6833e97148678656143)