„Punktsymmetrie“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
redirect auf #Punktsymmetrie |
Artikel wiederhergestellt, der Begriff verdient schon einen eigenen Artikel, dass es sehr viele Symmetrien gibt und diese hier in der Schule von Bedeutung ist |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:PuSyFiguren.svg|thumb|upright=1.2|Punktsymmetrische Objekte in der Ebene]] |
|||
#REDIRECT [[Symmetrie (Geometrie)#Punktsymmetrie]] |
|||
Die '''Punktsymmetrie''', auch '''Zentralsymmetrie'''<ref name="meyers">''Meyers großes Taschenlexikon in 24 Bänden''. BI-Taschenbuchverlag 1992, Band 21, S.258</ref> in der [[Geometrie]] eine Eigenschaft einer [[Geometrische Figur|Figur]]. Eine Figur ist punktsymmetrisch, wenn sie durch die [[Spiegelung (Geometrie)|Spiegelung]] an einem '''Symmetriepunkt''' auf sich selbst abgebildet wird. |
|||
== Definition == |
|||
Eine (ebene) [[geometrische Figur]] (zum Beispiel ein Viereck) heißt ''punktsymmetrisch'', wenn es eine [[Spiegelung (Geometrie)|Punktspiegelung]] gibt, die dieses Figur auf sich abbildet. Der Punkt, an dem diese Spiegelung erfolgt, wird als ''Symmetriezentrum'' bezeichnet.<ref>{{Literatur | Autor = Arnfried Kemnitz | Titel = Mathematik zum Studienbeginn | Jahr = 2011 | Verlag = Vieweg+Teubner | Ort = Wiesbaden | ISBN = 978-3-8348-8258-5 | Seiten = 144 }}</ref> |
|||
== Punktspiegelung als Drehung == |
|||
Eine Punktspiegelung entspricht einer Drehung der geometrischen Figur um 180°. Somit ist die Punktsymmetrie ein Spezialfall der [[Drehsymmetrie]]. |
|||
== Beispiele == |
|||
* Bei einem [[Viereck]] liegt Punktsymmetrie (in sich) genau dann vor, wenn es sich um ein [[Parallelogramm]] handelt. Das Symmetriezentrum ist in diesem Fall der Schnittpunkt seiner Diagonalen. Als Sonderfälle des Parallelogramms sind auch [[Rechteck]], [[Raute]] und [[Quadrat (Geometrie)|Quadrat]] punktsymmetrisch. |
|||
* Jeder Kreis ist (in sich) punktsymmetrisch bezüglich seines Mittelpunkts. |
|||
* Zwei Kreise mit gleichem Radius sind zueinander punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt der Verbindungsstrecke zwischen den beiden Kreismittelpunkten. |
|||
* Mehrere Symmetriezentren kann es nur geben, wenn die Figur nicht [[beschränkt]] ist. Das einfachste Beispiel ist die Gerade. Sie hat sogar unendlich viele Symmetriezentren. |
|||
* Ein [[Dreieck]] kann ist niemals punktsymmetrisch. Jedoch können aber zwei Dreiecke zueinander punktsymmetrisch sein. |
|||
== Punktsymmetrie von Funktionsgraphen == |
|||
=== Überblick === |
|||
[[Datei:PuSyFktGraph.svg|thumb|Punktsymmetrischer Funktionsgraph]] |
|||
Eine in der Schulmathematik häufige Aufgabenstellung besteht darin nachzuweisen, dass der [[Funktionsgraph|Graph]] einer gegebenen [[Funktion (Mathematik)|Funktion]] <math>f \colon D \to \R</math> mit dem [[Definitionsbereich]] <math>D \subset \R</math> und den [[Reelle Zahl|reellen Zahlen]] als [[Zielmenge|Wertebereich]] punktsymmetrisch ist. |
|||
Existiert ein Punkt <math>(a,b)</math>, so dass für die Funktion <math>f</math> die Gleichung |
|||
:<math>f(a+x) - b= - f(a-x) + b </math> |
|||
für alle <math>x \in D</math> gilt, dann ist die Funktion punktsymmetrisch zum Punkt <math>(a,b)</math>. |
|||
Die genannte Bedingung ist durch Substitution von <math>x</math> mit <math>x-a</math> gleichwertig zu |
|||
:<math>f(x) = 2b - f(2a-x)</math>. |
|||
Im Spezialfall von Punktsymmetrie um dem Ursprung <math>(0,0)</math> vereinfacht sich diese Gleichung zu |
|||
:<math>f(-x) = -f(x)</math>. |
|||
Ist sie für alle ''x'' gültig, liegt Punktsymmetrie zum Koordinatenursprung vor. Dann nennt man die Funktion <math>f</math> [[Gerade und ungerade Funktionen|ungerade Funktion]]. |
|||
=== Beispiele === |
|||
==== Punktsymmetrie zum Koordinatenursprung ==== |
|||
[[Datei:Graph2xE5.svg|thumb|Kurve von f(x) = 2x<sup>5</sup>]] |
|||
Gegeben sei die Funktion <math>f(x) = 2 x^5.</math> Dann gilt |
|||
:<math>f(-x) = 2 (-x)^5</math> |
|||
::<math> = 2 (-1)^5 x^5</math> |
|||
::<math> = 2 (-1) x^5</math> |
|||
::<math> = -2 x^5 = - f(x)</math> |
|||
Also ist der Funktionsgraph punktsymmetrisch zum Ursprung (0,0). |
|||
==== Punktsymmetrie zum Punkt (0,2) ==== |
|||
[[Datei:Graph2xE5 plus 2.svg|thumb|Kurve von f(x) = 2x<sup>5</sup> + 2]] |
|||
Gegeben sei die Funktion <math>f(x) = 2 x^5 + 2</math>. Wähle dann <math>a = 0</math> und <math>b = 2</math>. Dann gilt |
|||
:<math>2b - f(2a-x) = 4 - f(-x) = 4 - ( 2(-x)^5 + 2) </math> |
|||
:<math> = 4 - (-2x^5 + 2) </math> |
|||
:<math> = 4 + 2x^5 - 2 </math> |
|||
:<math> = 2x^5 + 2 = f(x)</math> |
|||
Folglich ist der Funktionsgraph punktsymmetrisch zum Punkt <math>(0,2)</math> und es gilt |
|||
:<math> -f(x)+2 = f(-x)-2 </math>. |
|||
Um den Symmetriepunkt <math>(0,2)</math> zu bestimmen, hilft dieses Verfahren nicht. Meist reicht es jedoch den Funktionsgraph zu zeichen und daraus eine Vermutung bezüglich des Symmetriepunkts abzuleiten. |
|||
== Einzelnachweise == |
|||
<references /> |
|||
Version vom 1. April 2013, 21:24 Uhr

Die Punktsymmetrie, auch Zentralsymmetrie[1] in der Geometrie eine Eigenschaft einer Figur. Eine Figur ist punktsymmetrisch, wenn sie durch die Spiegelung an einem Symmetriepunkt auf sich selbst abgebildet wird.
Definition
Eine (ebene) geometrische Figur (zum Beispiel ein Viereck) heißt punktsymmetrisch, wenn es eine Punktspiegelung gibt, die dieses Figur auf sich abbildet. Der Punkt, an dem diese Spiegelung erfolgt, wird als Symmetriezentrum bezeichnet.[2]
Punktspiegelung als Drehung
Eine Punktspiegelung entspricht einer Drehung der geometrischen Figur um 180°. Somit ist die Punktsymmetrie ein Spezialfall der Drehsymmetrie.
Beispiele
- Bei einem Viereck liegt Punktsymmetrie (in sich) genau dann vor, wenn es sich um ein Parallelogramm handelt. Das Symmetriezentrum ist in diesem Fall der Schnittpunkt seiner Diagonalen. Als Sonderfälle des Parallelogramms sind auch Rechteck, Raute und Quadrat punktsymmetrisch.
- Jeder Kreis ist (in sich) punktsymmetrisch bezüglich seines Mittelpunkts.
- Zwei Kreise mit gleichem Radius sind zueinander punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt der Verbindungsstrecke zwischen den beiden Kreismittelpunkten.
- Mehrere Symmetriezentren kann es nur geben, wenn die Figur nicht beschränkt ist. Das einfachste Beispiel ist die Gerade. Sie hat sogar unendlich viele Symmetriezentren.
- Ein Dreieck kann ist niemals punktsymmetrisch. Jedoch können aber zwei Dreiecke zueinander punktsymmetrisch sein.
Punktsymmetrie von Funktionsgraphen
Überblick

Eine in der Schulmathematik häufige Aufgabenstellung besteht darin nachzuweisen, dass der Graph einer gegebenen Funktion mit dem Definitionsbereich und den reellen Zahlen als Wertebereich punktsymmetrisch ist. Existiert ein Punkt , so dass für die Funktion die Gleichung
für alle gilt, dann ist die Funktion punktsymmetrisch zum Punkt .
Die genannte Bedingung ist durch Substitution von mit gleichwertig zu
- .
Im Spezialfall von Punktsymmetrie um dem Ursprung vereinfacht sich diese Gleichung zu
- .
Ist sie für alle x gültig, liegt Punktsymmetrie zum Koordinatenursprung vor. Dann nennt man die Funktion ungerade Funktion.
Beispiele
Punktsymmetrie zum Koordinatenursprung

Gegeben sei die Funktion Dann gilt
Also ist der Funktionsgraph punktsymmetrisch zum Ursprung (0,0).
Punktsymmetrie zum Punkt (0,2)
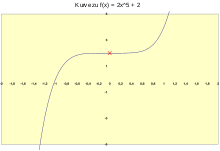
Gegeben sei die Funktion . Wähle dann und . Dann gilt
Folglich ist der Funktionsgraph punktsymmetrisch zum Punkt und es gilt
- .
Um den Symmetriepunkt zu bestimmen, hilft dieses Verfahren nicht. Meist reicht es jedoch den Funktionsgraph zu zeichen und daraus eine Vermutung bezüglich des Symmetriepunkts abzuleiten.
Einzelnachweise
- ↑ Meyers großes Taschenlexikon in 24 Bänden. BI-Taschenbuchverlag 1992, Band 21, S.258
- ↑ Arnfried Kemnitz: Mathematik zum Studienbeginn. Vieweg+Teubner, Wiesbaden 2011, ISBN 978-3-8348-8258-5, S. 144.
























