„Spektrales Clustering“ – Versionsunterschied
| [ungesichtete Version] | [ungesichtete Version] |
Satz gelöscht, da Duplikat. |
Chire (Diskussion | Beiträge) K literatur-vorlage statt text. Hatte das gerade im copy&paste puffer. |
||
| Zeile 368: | Zeile 368: | ||
== Literatur == |
== Literatur == |
||
=== Grundlagen und Verfahren === |
=== Grundlagen und Verfahren === |
||
* {{Literatur |
|||
| ⚫ | |||
| Autor=Martin Ester, Jörg Sander |
|||
| ⚫ | |||
| Verlag=[[Springer]] |
|||
| Ort=Berlin |
|||
| Jahr=2000 |
|||
| ISBN=3540673288 |
|||
}} |
|||
* Backhaus, K., Erichson, B., Plinke, W., Weiber, R. ''Multivariate Analysemethoden. Eine anwendungsorientierte Einführung''. Springer ISBN 3-540-00491-2 |
* Backhaus, K., Erichson, B., Plinke, W., Weiber, R. ''Multivariate Analysemethoden. Eine anwendungsorientierte Einführung''. Springer ISBN 3-540-00491-2 |
||
* Bickel, S., Scheffer, T., ''Multi-View Clustering''. Proceedings of the IEEE International Conference on Data Mining, 2004 |
* Bickel, S., Scheffer, T., ''Multi-View Clustering''. Proceedings of the IEEE International Conference on Data Mining, 2004 |
||
* Shi, J., Malik, J. ''Normalized Cuts and Image Segmentation'', in Proc. of IEEE Conf. on Comp. Vision and Pattern Recognition, Puerto Rico 1997 |
* Shi, J., Malik, J. ''Normalized Cuts and Image Segmentation'', in Proc. of IEEE Conf. on Comp. Vision and Pattern Recognition, Puerto Rico 1997 |
||
* Xu, L., Neufeld, J., Larson, B. and Schuurmans, D., ''Maximum margin clustering.'' in [http://books.nips.cc/nips17.html Advances in Neural Information Processing Systems 17] (NIPS*2004), 2004 |
* Xu, L., Neufeld, J., Larson, B. and Schuurmans, D., ''Maximum margin clustering.'' in [http://books.nips.cc/nips17.html Advances in Neural Information Processing Systems 17] (NIPS*2004), 2004 |
||
=== Anwendung === |
=== Anwendung === |
||
* Bacher, J., Pöge, A., Wenzig, K., ''Clusteranalyse - Anwendungsorientierte Einführung in Klassifikationsverfahren'', 3. Auflage. München, Oldenbourg 2010, ISBN 978-3-486-58457-8 |
* Bacher, J., Pöge, A., Wenzig, K., ''Clusteranalyse - Anwendungsorientierte Einführung in Klassifikationsverfahren'', 3. Auflage. München, Oldenbourg 2010, ISBN 978-3-486-58457-8 |
||
Version vom 28. Februar 2011, 00:17 Uhr
Unter Clusteranalyse (Clustering-Algorithmus, gelegentlich auch: Ballungsanalyse) versteht man Verfahren zur Strukturentdeckung in (großen) Datenbeständen. Die so gefundenen Gruppen von „ähnlichen“ Objekten werden als Cluster bezeichnet, die Gruppenzuordnung als Clustering. Die gefundene Gruppierung kann auch hierarchisch sein, also Untergruppen in Gruppen beschreiben.
Bei der Clusteranalyse ist das Ziel neue Gruppen in den Daten zu identifizieren (im Gegensatz zur Klassifikation, bei der Daten bestehenden Klassen zugeordnet werden). Man spricht von einem „uninformierten Verfahren“, da es nicht auf Klassen-Vorwissen angewiesen ist. Diese neuen Gruppen können anschließend beispielsweise zur automatisierten Klassifizierung, zur Erkennung von Mustern in der Bildverarbeitung oder zur Marktsegmentierung eingesetzt werden (oder in beliebigen anderen Verfahren, die auf ein derartiges Vorwissen angewiesen sind).
Die zahlreichen Algorithmen unterscheiden sich vor allem in ihrem Ähnlichkeits- und Gruppenbegriff, ihrem Datenmodell, ihrem algorithmischen Vorgehen (und damit ihrer Komplexität) und der Toleranz gegenüber Störungen in den Daten. Ob das von einem solchen Algorithmus generierte „Wissen“ nützlich ist, kann jedoch in der Regel nur ein Experte beurteilen. Ein Clusteringalgorithmus kann unter Umständen vorhandenes Wissen reproduzieren (beispielsweise Personendaten in die bekannten Gruppen „männlich“ und „weiblich“ unterteilen), oder auch für den Anwendungszweck nicht hilfreiche Gruppen generieren. Die gefundenen Gruppen lassen sich oft auch nicht verbal beschreiben (z.B. „männliche Personen“) sondern gemeinsame Eigenschaften erst durch nachträgliche Analyse identifizieren. Bei der Anwendung von Clusteranalyse ist es daher oft notwendig, verschiedene Verfahren und verschiedene Parameter zu probieren, die Daten vorzuverarbeiten und beispielsweise Attribute auszuwählen oder wegzulassen.
Beispiel
Angewendet auf einen Datensatz von Fahrzeugen, könnte ein Clustering-Algorithmus (und eine nachträgliche Analyse der gefundenen Gruppen) beispielsweise folgende Struktur liefern
| Fahrzeuge | |||||||||||||||||||||||||||||||||
| Fahrräder | |||||||||||||||||||||||||||||||||
| LKW | PKW | Rikschas | Rollermobile | ||||||||||||||||||||||||||||||
Wobei aber Folgendes zu beachten ist:
- Der Algorithmus selbst liefert keine Interpretation („LKW“) der gefundenen Gruppen. Hierzu ist eine separate Analyse der Gruppen notwendig!
- Ein Mensch würde eine Fahrradrikscha als Untergruppe der Fahrräder ansehen. Für einen Clusteringalgorithmus aber sind 3 Räder oft ein signifikanter Unterschied, den sie mit einem Dreirad-Rollermobil teilen.
- Die Gruppen sind oftmals nicht „rein“, es können also beispielsweise kleine LKW in der Gruppe der PKW sein.
- Es treten oft zusätzliche Gruppen auf, die nicht erwartet wurden („Polizeiautos“, „Cabrios“, „rote Autos“, „Autos mit Xenon-Scheinwerfern“).
- Manche Gruppen werden nicht gefunden, beispielsweise „Motorräder“ oder „Liegeräder“.
- Welche Gruppen gefunden werden hängt stark vom verwendeten Algorithmus, Parametern und verwendeten Objekt-Attributen ab.
- Oft wird auch nichts (sinnvolles) gefunden.
- In diesem Beispiel wurde nur bekanntes Wissen (wieder-)gefunden – als Verfahren zur „Wissensentdeckung“ ist die Clusteranalyse hier also eigentlich gescheitert.
Geschichte
Historisch gesehen stammt das Verfahren aus der Taxonomie in der Biologie, wo über eine Clusterung von verwandten Arten eine Ordnung der Lebewesen ermittelt wird. Allerdings wurden dort ursprünglich keine automatischen Berechnungsverfahren eingesetzt. Inzwischen können zur Bestimmung der Verwandtschaft von Organismen unter anderem ihre Gensequenzen verglichen werden. Siehe auch: Kladistik
Prinzip/Funktionsweise
Mathematische Modellierung
Die Eigenschaften der zu untersuchenden Objekte werden mathematisch als Zufallsvariablen aufgefasst. Sie werden in der Regel in Form von Vektoren als Punkte in einem Vektorraum dargestellt, deren Dimensionen die Eigenschaftsausprägungen des Objekts bilden. Bereiche, in denen sich Punkte anhäufen (Punktwolke), werden Cluster genannt. Bei Streudiagrammen dienen die Abstände der Punkte zueinander oder die Varianz innerhalb eines Clusters als sogenannte Proximitätsmaße, welche die Ähnlichkeit bzw. Unterschiedlichkeit zwischen den Objekten zum Ausdruck bringen.
Ein Cluster kann auch als eine Gruppe von Objekten definiert werden, die in Bezug auf einen berechneten Schwerpunkt eine minimale Abstandssumme haben. Dazu ist die Wahl eines Distanzmaßes erforderlich. In bestimmten Fällen sind die Abstände (bzw. umgekehrt die Ähnlichkeiten) der Objekte untereinander direkt bekannt, so dass sie nicht aus der Darstellung im Vektorraum ermittelt werden müssen.
Grundsätzliche Vorgehensweise
In einer Gesamtmenge/gruppe mit unterschiedlichen Objekten, werden die Objekte, die sich ähnlich sind, zu Gruppen (Clustern) zusammengefasst.
Als Beispiel sei folgende Musikanalyse gegeben. Die Werte ergeben sich aus dem Anteil der Musikstücke, die der Nutzer pro Monat online kauft.
| Person 1 | Person 2 | Person 3 | |
|---|---|---|---|
| Pop | 2 | 1 | 8 |
| Rock | 10 | 8 | 1 |
| Jazz | 3 | 3 | 1 |
In diesem Beispiel würde man die Personen intuitiv in zwei Gruppen einteilen. Gruppe1 besteht aus Person 1&2 und Gruppe 2 besteht aus Person 3. Das würden auch die meisten Clusteralgorithmen machen. Dieses Beispiel ist lediglich aufgrund der gewählten Werte so eindeutig, spätestens mit näher zusammenliegenden Werten und mehr Variablen (hier Musikrichtungen) und Objekten (hier Personen), ist leicht vorstellbar, dass die Einteilung in Gruppen nicht mehr so trivial ist.
Etwas genauer und abstrakter ausgedrückt: Die Objekte einer heterogenen (beschrieben durch unterschiedliche Werte ihrer Variablen) Gesamtmenge werden mit Hilfe der Clusteranaylse zu Teilgruppen (Cluster/Segmente) zusammengefasst, die in sich möglichst homogen (die Unterschiede der Variablen möglichst gering) sind. In unserem Musikbeispiel kann die Gruppe aller Musikhörer (eine sehr heterogene Gruppe) in die Gruppen der Jazzhörer, Rockhörer, Pophörer, etc. (jeweils relativ homogen) unterteilt werden bzw. werden die die Hörer mit ähnlichen Präferenzen zu der entsprechende Gruppe zusammengefasst.
Eine Clusteranalyse (z.B. bei der Marktsegmentierung) erfolgt dabei in folgenden Schritten:
Schritte zur Clusterbildung:
- Variablenauswahl: Auswahl (und Erhebung) der für die Untersuchung geeigneten Variablen. Sofern die Variablen der Objekte/Elemente noch nicht bekannt/vorgegeben sind, müssen alle für die Untersuchung wichtigen Variablen bestimmt und anschließend ermittelt werden.
- Proximitätsbestimmung: Wahl des Proximitätsmaßes und Bestimmung der Distanz- bzw. Ähnlichkeitswerte (je nach Proximitätsmaß) zwischen den Objekten über ein geeignetes Proximitätsmaß. Abhängig von der Art der Variablen, bzw. der Skalenart der Variablen, wird eine entsprechende Distanzfunktion zur Bestimmung des Abstandes (Distanz) zweier Elemente, oder eine Ähnlichkeitsfunktion zur Bestimmung der Ähnlichkeit verwendet. Die Variablen werden zunächst einzeln Verglichen und aus der Distanz der einzelnen Variablen die Gesamtdistanz (oder Ähnlichkeit) berechnet. Die Funktion zur Bestimmung von Distanz oder Ähnlichkeit wird auch Proximitätsmaß genannt. Der durch ein Proximitätsmaß ermittelte Distanz-, bzw. Ähnlichkeitwert nennt sich Proximität. Werden alle Objekte miteinander verglichen ergibt sich eine Proximitätsmatrix, welche jeweils zwei Objekten eine Proximität zuweist.
- Clusterbildung: Bestimmung und Durchführung eines/der geeigneten Clusterverfahrens, um anschließend mit Hilfe des/dieser Verfahrens Gruppen/Cluster bilden zu können (die Proximitätsmatrix wird hierdurch reduziert). Im Regelfall werden hierbei mehrere Verfahren kombiniert, z.B.:
- Finden von Ausreißern durch das Single-Linkage Verfahren (Hierarchisches Verfahren)
- Bestimmung der Clusterzahl durch das Ward-Verfahren (Hierarchisches Verfahren)
- Bestimmung der Clusterzusammensetzung durch das Austauschverfahren (Partitionierendes Verfahren)
Weitere Schritte der Clusteranalyse:
- Bestimmung der Clusterzahl durch Betrachtung der Varianz innerhalb und zwischen den Gruppen. Hier wird bestimmt, wie viele Gruppen tatsächlich gebildet werden, denn bei der Clusterung selbst ist keine Abbruchbedingung vorgegeben. Z.B. wird bei einem agglomerativen Verfahren folglich so lange fusioniert, bis nur noch eine Gesamtgruppe vorhanden ist.
- Interpretation der Cluster (abhängig von den inhaltlichen Ergebnissen, z.B. durch t-Wert)
- Beurteilung der Güte der Clusterlösung (Bestimmung der Trennschärfe der Variablen, Gruppenstabilität)
Unterschiedliche Proximitätsmaße/Skalen
Die Skalen bezeichnen den Wertebereich, den die betrachtete(n) Variable(n) des Objektes annehmen kann. Je nachdem welche Art von Skala vorliegt, muss man ein passendes Proximitätsmaß verwenden. Es gibt drei Hauptkategorien von Skalen:
- Binäre Skalen
- die Variable kann zwei Werte z.B. 0 oder 1 annehmen z.B. männlich/weiblich.
- Verwendete Proximitätsmaße (Beispiele):
- Jaccard-Koeffizient (Ähnlichkeitsmaß)
- Lance-Williams-Maß (Distanzmaß)
- Nominale Skalen
- die Variable kann unterschiedliche Werte annehmen um eine qualitative Unterscheidung zu treffen, z.B. ob Pop, Rock oder Jazz bevorzugt wird.
- Verwendete Proximitätsmaße (Beispiele):
- Chi-Quadrat-Maß (Distanzmaß)
- Phi-Quadrat-Maß (Distanzmaß)
- Metrische Skalen
- die Variable nimmt einen Wert auf einer vorher festgelegten Skala eine quantitative Aussage zu treffen z.B. wie gerne eine Person Pop auf einer Skala von 1 bis 10 hört.
- Verwendete Proximitätsmaße (Beispiele):
- Pearson Korrelationskoeffizient (Ähnlichkeitsmaß)
- Euklidische Metrik (Distanzmaß)
- Minkowski-Metrik (Distanzmaß)
Formen der Gruppenbildung (Gruppenzugehörigkeit)
Es sind drei unterschiedliche Formen der Gruppenbildung (Gruppenzugehörigkeit) möglich. Bei den nichtüberlappenden Gruppen wird jedes Objekt nur einer Gruppe (Segment,Cluster) zugeordnet, bei den überlappenden Gruppen kann ein Objekt mehreren Gruppen zugeordnet werden, und bei dem Fuzzygruppen gehört ein Element jeder Gruppe mit einer bestimmten Wahrscheinlichkeit an.
| Nichtüberlappend | |||||||||||||
| Formen der Gruppenbildung | Überlappend | ||||||||||||
| Fuzzy | |||||||||||||
Man unterscheidet man zwischen "harten" und "weichen" Clusteringalgorithmen. Harte Methoden (z. B. k-means, Spectral Clustering, Kernel PCA) ordnen jeden Datenpunkt genau einem Cluster zu, wohingegen bei weichen Methoden (z. B. EM-Algorithmus mit mixture-of-Gaussians model) jedem Datenpunkt für jeden Cluster eine Wahrscheinlichkeit zugeordnet wird mit der dieser Datenpunkt in diesem Cluster liegt. Weiche Methoden sind insbesondere dann nützlich wenn die Datenpunkte relativ homogen im Raum verteilt sind und die Cluster nur als Regionen mit erhöhter Datenpunktdichte in Erscheinung treten, d.h. wenn es z. B. fließende Übergänge zwischen den Clustern oder Hintergrundrauschen gibt (harte Methoden sind in diesem Fall unbrauchbar).
Unterscheidung der Clusterverfahren
Clusterverfahren lassen sich in graphentheoretische, hierarchische, partitionierende, und optimierende Verfahren sowie in weitere Unterverfahren einteilen.
- Partitionierende Verfahren
- verwenden eine gegebene Partitionierung und ordnen die Elemente durch Austauschfunktionen um, bis die verwendete Zielfunktion ein Optimum erreicht. Zusätzliche Gruppen können jedoch nicht gebildet werden, da die Anzahl der Cluster bereits am Anfang festgelegt wird (vgl. hierarchische Verfahren).
- Hierarchische Verfahren
- gehen von der gröbsten (agglomerativ bzw. bottom-up) bzw. feinsten (divisiv bzw. top-down) Partition aus (vgl. Top-down und Bottom-up). Die gröbste Partition entspricht der Gesamtheit aller Elemente und die feinste Partition enthält lediglich ein Element bzw. jedes Element bildet seine eigene Gruppe/Partition. Durch Aufteilen bzw. Zusammenfassen lassen sich anschließend Cluster bilden. Einmal gebildete Gruppen können nicht mehr aufgelöst oder einzelne Elemente getauscht werden (vgl. partitionierende Verfahren). Agglomerative Verfahren kommen in der Praxis (z.B. der Marktsegementierung im Marketing) sehr viel häufiger vor.
| graphentheoretisch | |||||||||||||||||||||
| divisiv | |||||||||||||||||||||
| hierarchisch | |||||||||||||||||||||
| agglomerativ | |||||||||||||||||||||
| Clusterverfahren | |||||||||||||||||||||
| Austauschverfahren | |||||||||||||||||||||
| partitionierend | |||||||||||||||||||||
| iterierte Minimaldistanzverfahren | |||||||||||||||||||||
| optimierend | |||||||||||||||||||||
Zu beachten ist, dass man noch diverse weitere Verfahren und Algorithmen unterscheiden kann, unter anderem überwachten (supervised) und nicht-überwachten (unsupervised) Algorithmen oder modellbasierte Algorithmen, bei denen eine Annahme über die zugrundeliegende Verteilung der Daten gemacht wird (z. B. mixture-of-Gaussians model).
Algorithmen/Verfahren
Graphentheoretische Cluster
DBSCAN – Dichteverbundene Cluster
Grundlagen Bei dichtebasiertem Clustering werden Cluster als Objekte in einem d-dimensionalen Raum betrachtet, welche dicht beieinander liegen, getrennt durch Gebiete mit geringerer Dichte.
Grundbegriffe
- Ein Objekt o ∈ O heißt Kernobjekt, wenn gilt: |Nε(o)| ≥ MinPts, wobei Nε(o) = {o’ ∈ O | dist(o, o’) ≤ ε}.
- Ein Objekt p ∈ O ist direkt dichte-erreichbar von q ∈ O bzgl. ε und MinPts, wenn gilt: p ∈ Nε(q) und q ist ein Kernobjekt in O.
- Ein Objekt p ist dichte-erreichbar von q, wenn es eine Kette von direkt erreichbaren Objekten zwischen q und p gibt.
- Zwei Objekte p und q sind dichte-verbunden, wenn sie beide von einem dritten Objekt o aus dichte-erreichbar sind.
- Ein Cluster C bzgl. ε und MinPts ist eine nicht-leere Teilmenge von O, für die die folgenden Bedingungen erfüllt sind:
- Maximalität: ∀ p, q ∈ O: wenn p ∈ C und q dichte-erreichbar von p ist, dann ist auch q ∈ C.
- Verbundenheit: ∀ p, q ∈ C: p ist dichte-verbunden mit q.
Eine wichtige Erweiterung von DBSCAN ist der Algorithmus OPTICS, der auch Cluster unterschiedlicher Dichte erkennen kann, ein hierarchisches Ergebnis liefert, und eine visuelle Evaluierung erlaubt.
Cliquen und Zusammenhangskomponenten
Zwei Extreme bei der Clusterung in Netzwerken bilden die Einteilung in Zusammenhangskomponenten (Single Link) und in Cliquen.
Hierarchische Clusterverfahren
Agglomeratives Verfahren
Beschreibung der agglomerativen Verfahren
Beim Anhäufen der Cluster wird zunächst jedes Objekt als ein eigener Cluster mit einem Element aufgefasst. Nun werden in jedem Schritt die jeweils einander nächsten Cluster zu einem Cluster zusammengefasst. Das Verfahren kann beendet werden, wenn alle Cluster eine bestimmte Distanz/Ähnlichkeit zueinander überschreiten/unterschreiten oder wenn eine genügend kleine Zahl von Clustern ermittelt worden ist. Dies ist bei Clustern mit nur einem Objekt, wie sie zu Anfang vorgegeben sind, trivial. Sobald ein Cluster aus mehreren Objekten besteht, muss jedoch entschieden werden, welches Objekt aus dem Cluster zur Proximitätsmessung mit dem nächsten Objekt/Cluster verwendet wird. Hier gibt es unterschiedliche Möglichkeiten, in denen sich die einzelnen agglomerative Verfahren unterscheiden.
Beispiel zu den einzelnen Verfahren
Besonders deutlich wird dies im zweiten Schritt des Algorithmus. Z.B. im Fall der Verwendung eines Distanzmasses wurden im ersten Schritt die beiden einander nächsten Objekte zu einem Cluster fusioniert, die beiden, welche die geringste Distanz zueinander hatten. Vorstellbar ist dies als Distanzmatrix:
| Distanz zw. | Cluster1 Objekt1 |
Cluster2 Objekt2 |
Cluster3 Objekt3 |
Cluster4 Objekt4 |
|---|---|---|---|---|
| Objekt1 | 0 | |||
| Objekt2 | 4 | 0 | ||
| Objekt3 | 7 | 5 | 0 | |
| Objekt4 | 8 | 10 | 9 | 0 |
In diesem Fall würde man Objekt1 und Objekt2 zu einem Cluster zusammenfassen (fusionieren). Nun muss die Matrix neu erstellt werden ("o." steht für oder):
| Distanz zw. | Cluster1 Objekt1&2 |
Cluster2 Objekt3 |
Cluster3 Objekt4 |
|---|---|---|---|
| Objekt1&2 | 0 | ||
| Objekt3 | 7 o. 5 | 0 | |
| Objekt4 | 8 o. 10 | 9 | 0 |
Welcher der beiden Werte für die Distanzbestimmung relevant ist, bestimmt das Verfahren:
- Single Linkage Verfahren
- Das Single Linkage würde den kleinsten/kleineren Wert aus dem Cluster zur Bestimmung der neuen Abstände zu den anderen Objekten verwenden, als die 5 und die 8.
Distanz zw. Cluster1
Objekt1&2Cluster2
Objekt3Cluster3
Objekt4Objekt1&2 0 Objekt3 5 0 Objekt4 8 9 0
- Complete Linkage Verfahren
- Das Complete Linkage würde den größten Wert aus dem Cluster zur Bestimmung der neuen Abstände zu den anderen Objekten verwenden, als die 7 und die 10.
Distanz zw. Cluster1
Objekt1&2Cluster2
Objekt3Cluster3
Objekt4Objekt1&2 0 Objekt3 7 0 Objekt4 10 9 0
- Average Linkage Verfahren
- Verwendet einen Durchschnittswert (die genaue Berechnung findet sich im nächsten Abschnitt).
- Centroid Verfahren
- Medoid Verfahren
- Median Verfahren
- Ward Verfahren
| Verfahren | Verwendbares Proximitätsmaß | Anmerkung zum Verfahren |
|---|---|---|
| Single Linkage | Distanz- / Ähnlichkeitsmaß | neigt zur Kettenbildung |
| Complete Linkage | Distanz- / Ähnlichkeitsmaß | neigt zur Bildung von kleinen Gruppen |
| Centroid | Distanz- / Ähnlichkeitsmaß | Beispiel |
| Average Linkage | Distanz | Beispiel |
| Medoid | Beispiel | Beispiel |
| Median | Distanz | Beispiel |
| Ward | Distanz | neigt zur Bildung von gleich großen Gruppen |
Mathematische Beschreibung der agglomerativen Verfahren
Berechnet werden kann der Abstand zweier Cluster und beispielsweise über eine der folgenden Distanzfunktionen ( ist hierbei der Abstand von zwei einzelnen Objekten):
- Der minimale Abstand zweier Elemente aus den beiden Clustern (single linkage clustering)
-
Single Linkage Abstand
- Der maximale Abstand zweier Elemente aus den beiden Clustern (complete linkage clustering)
-
Complete Linkage Abstand
- Der durchschnittliche Abstand aller Elementpaare aus den beiden Clustern (average linkage clustering)
-
Mittelwert-Abstand
- Der durchschnittliche Abstand aller Elementpaare aus der Vereinigung von A und B (average group linkage)
- Der Abstand der Mittelwerte der beiden Cluster (centroid method)
Wobei der Mittelwert des Clusters sei, des Clusters .
- Die Zunahme der Varianz beim Vereinigen von A und B (Ward’s method)
Wobei der Mittelwert des Clusters sei, des Clusters .
Weitere Methoden: Density Linkage, Uniform-Kernel, Wong’s Hybrid, EML, Flexible-Beta, McQuitty’s Similarity Analysis, Medoid
Von praktischer Relevanz ist hierbei vor allem "single linkage", da es mit dem Algorithmus SLINK eine effiziente Berechnungsmethode gibt.
Visualisierung
Zur Visualisierung der bei einer hierarchischen Clusterung entstehenden Baumstruktur kann das Dendrogramm (griech. δένδρον (dendron) = Baum) genutzt werden. Das Dendrogramm ist ein Baum, der die hierarchische Zerlegung der Datenmenge in immer kleinere Teilmengen darstellt. Die Wurzel repräsentiert ein einziges Cluster, das die gesamte Menge enthält. Die Blätter des Baumes repräsentieren Cluster, in denen sich je ein einzelnes Objekt der Datenmenge befindet. Ein innerer Knoten repräsentiert die Vereinigung aller seiner Kindknoten. Jede Kante zwischen einem Knoten und einem seiner Kindknoten hat als Attribut noch die Distanz zwischen den beiden repräsentierenden Mengen von Objekten.
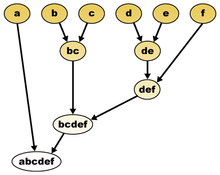
Dendrogramm: Die Objekte b und c, sowie d und e liegen sehr dicht zusammen, während f und a sich weiter entfernt davon befinden, siehe [1].
Partitionierende Clusterverfahren
k-means-Algorithmus
Beim k-means Algorithmus wird die Anzahl von Clustern vor dem Start festgelegt. Eine Funktion zur Berechnung des Abstands zweier Messungen muss gegeben und kompatibel zur Mittelwertbildung sein.
Der Algorithmus läuft folgendermaßen ab:
- Initialisierung: (zufällige) Auswahl von Clusterzentren
- Zuordnung: Jedes Objekt wird dem ihm am nächsten liegenden Clusterzentrum zugeordnet
- Neuberechnung: Es werden für jeden Cluster die Clusterzentren neu berechnet
- Wiederholung: Falls sich nun die Zuordnung der Objekte ändert, weiter mit Schritt 2, sonst Abbruch
Eigenheiten k-means-Algorithmus
- Der k-means-Algorithmus liefert für unterschiedliche Startpositionen der Clusterzentren möglicherweise unterschiedliche Ergebnisse.
- Es muss k geeignet gewählt werden, und die Qualität des Ergebnisses hängt stark von den Startpositionen ab.
- Es kann sein, dass ein Cluster in einem Schritt leer bleibt und somit (mangels Berechenbarkeit eines Clusterzentrums) nicht mehr gefüllt werden kann.
- Ein optimales Clustering zu finden gehört zur Komplexitätsklasse NP. Der k-means Algorithmus findet nicht notwendigerweise die optimale Lösung, ist aber sehr schnell.
Um diese Probleme zu umgehen, startet man den k-means-Algorithmus einfach neu in der Hoffnung, dass beim nächsten Lauf durch andere zufällige Clusterzentren ein anderes Ergebnis geliefert wird. Wegen der obigen theoretischen Unzulänglichkeiten gilt der k-means-Algorithmus als „quick’n’dirty“-Heuristik, weil er dennoch oft brauchbare Resultate liefert.
Der isodata-Algorithmus kann als Spezialfall von k-means angesehen werden.
EM-Algorithmus
Der EM-Algorithmus modelliert Cluster mit Hilfe von multivariaten Normalverteilungen, die ähnlich k-Means iterativ verfeinert werden. Analog zu k-Means muss auch hier im Vorneherein festgelegt werden, wie viele Normalverteilungen zur Modellierung verwendet werden sollen.
Zur Berechnung von Mittelwerten und Kovarianzmatrizen müssen des weiteren die Datenobjekte als Vektoren einer festen Dimension aufgefasst werden können.
Im Gegensatz zu k-means wird damit eine „weiche“ Clusterzuordnung erreicht: Mit einer gewissen Wahrscheinlichkeit gehört jedes Objekt zu jedem Cluster. Jedes Objekt beeinflusst so die Parameter jedes Clusters entsprechend dieser Wahrscheinlichkeit. Der Erfolg des Algorithmus hängt stark von der angenommenen Wahrscheinlichkeitsverteilung ab.
Spectral Clustering
Dieser Algorithmus wird häufig in der Bildverarbeitung eingesetzt, kann aber auch zum Clustern von Websuchergebnissen verwendet werden.
- Input: Adjazenzmatrix A, die die paarweisen Ähnlichkeiten der zu clusternden Objekte enthält
- Finde einen Schnitt durch diesen Graphen so, dass möglichst wenig Verbindungen zwischen ähnlichen Instanzen durchtrennt werden
- solange nicht die gewünschte Anzahl Clustern erreicht ist: zurück zu 2.
Maximum Margin Clustering
Problemstellung: Beim Clustering existieren keine Labels zu den Beispielen. Die Aufgabe ist es, ein Labeling der Instanzen zu finden, das den größten Abstand (margin) zwischen den Clustern ermöglicht.
Naiver Ansatz zur Lösung des Problems:
- Input: Eine Menge von ungelabelten Beispielen
- Finde eine mögliche Clusteraufteilung und bezeichne alle Beispiele eines Clusters mit dem gleichen Label!
- Trainiere einen Large Margin Classifier (z. B. Support Vector Machine) auf den so entstandenen gelabelten Beispielen und bestimme die Größe des Margins!
- Zurück zu 2, solange die ideale Clusteraufteilung nicht gefunden wurde.
Multiview Clustering
Übliche Clusteralgorithmen können nur in einem Vektorraum clustern. Der Multiviewansatz ermöglicht das parallele Clustern in verschiedenen Vektorräumen. Webseiten können z. B. im TF-IDF-Raum dargestellt werden. Dann wird jedem Eintrag im Featurevektor die Häufigkeit des Wortes im gegebenen Dokument zugewiesen. Andererseits können sie auch als Summe ihrer eingehenden Links aufgefasst werden – dann enthält jeder Eintrag im Featurevektor genau dann eine 1, wenn von der entsprechenden Quellseite ein Link auf die aktuelle Seite existiert. Kombiniert man diese beiden Views mittels Multiview Clustering, so sind die resultierenden Ergebnisse nachweisbar qualitativ besser als bei einfacher Konkatenation der Featurevektoren.
Ablauf des Algorithmus am Beispiel Webseiten:
- Initialisiere die Mittelwertvektoren eines k-Means Algorithmus auf Basis der TFIDF Vektoren
- Ordne die Instanzen entsprechend ihrer TFIDF Repräsentation dem ihnen am nächsten gelegenen Cluster zu
- Initialisiere die Mittelwertvektoren eines zweiten k-Means auf Basis der in 2 entstandenen Clusterzuordnungen und der Linkvektoren
- Ordne die Instanzen entsprechend ihren Linkvektoren dem ihnen am nächsten gelegenes Cluster zu
- zurück zu 1, solange sich die Zuordnung der Instanzen zu Clustern noch ändert.
Self-Organizing Maps (SOMs)
Fuzzy Clustering
Objektmengen können Elemente enthalten, die aufgrund mehrdeutiger Datenbefunde für keines der ermittelten Cluster prototypisch sind und mehreren Clustern zugeordnet werden könnten. Beim Fuzzy-Clustering werden Objekte unscharf (also mit einem bestimmten Zugehörigkeitsgrad) auf Cluster verteilt. Im Spezialfall der Zugehörigkeit = 1 bzw. der Zugehörigkeit = 0 ist das Element einem Cluster vollständig bzw. überhaupt nicht zugehörig. Der bekannteste Fuzzy-Clustering Algorithmus ist der Fuzzy C-Means Algorithmus.
Literatur
Grundlagen und Verfahren
- Martin Ester, Jörg Sander: Knowledge Discovery in Databases. Techniken und Anwendungen. Springer, Berlin 2000, ISBN 3-540-67328-8.
- Backhaus, K., Erichson, B., Plinke, W., Weiber, R. Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. Springer ISBN 3-540-00491-2
- Bickel, S., Scheffer, T., Multi-View Clustering. Proceedings of the IEEE International Conference on Data Mining, 2004
- Shi, J., Malik, J. Normalized Cuts and Image Segmentation, in Proc. of IEEE Conf. on Comp. Vision and Pattern Recognition, Puerto Rico 1997
- Xu, L., Neufeld, J., Larson, B. and Schuurmans, D., Maximum margin clustering. in Advances in Neural Information Processing Systems 17 (NIPS*2004), 2004
Anwendung
- Bacher, J., Pöge, A., Wenzig, K., Clusteranalyse - Anwendungsorientierte Einführung in Klassifikationsverfahren, 3. Auflage. München, Oldenbourg 2010, ISBN 978-3-486-58457-8
- Bortz, J. (1999), Statistik für Sozialwissenschaftler. (Kap. 16, Clusteranalyse). Berlin: Springer
- Härdle, W.; Simar, L. Applied Multivariate Statistical Analysis, Springer, New York, 2003
- Homburg, C., Krohmer. H. Marketingmanagement: Strategie - Instrumente - Umsetzung - Unternehmensführung, 3 Edition, Kapitel 8.2.2, Gabler, Wiesbaden, 2009
- Moosbrugger, H., Frank, D.: Clusteranalytische Methoden in der Persönlichkeitsforschung. Eine anwendungsorientierte Einführung in taxometrische Klassifikationsverfahren. Huber, Bern 1992, ISBN 3-456-82320-7.



















