Trugschluss (Mathematik)

In vielen Zweigen der Mathematik gibt es mathematische Trugschlüsse und Fehlschlüsse. Trug- und Fehlschlüsse werden in der Philosophie zusammen als Fallazien ( englisch fallacy, lateinisch fallacia=Täuschung ) bezeichnet. Scheinbeweise sind in der Mathematik Beweise, in denen Fallazien auftreten. Nicht wenige Fehlschlüsse haben in der Geschichte der Mathematik eine Rolle gespielt und waren Ausgangspunkte mathematischer Forschung. In der mathematischen Didaktik gehört das Aufdecken von Scheinbeweisen zu den Problemlöseaktivitäten.

Bei Fehlschlüssen handelt derjenige, der sie begeht, in gutem Glauben während bei Trugschlüssen die Absicht zu Täuschen wesentlich ist. Diese Unterscheidung ist freilich nicht scharf. Trugschlüsse führen durch eine plausibel erscheinende List zu einem falschen Ergebnis. Die Kunst dabei ist, den Fehler so zu verdecken, dass er zunächst nicht auffällt, und erst beim absurden Resultat offenkundig wird. Insbesondere Laien und Anfängern ist mitunter nicht sofort ersichtlich, wo der Fehler steckt. Trugschlüsse können als mathematischer Witz vorgetragen werden, in denen typische mathematische Schlussweisen in einem absurden Kontext angewendet werden.

In der elementaren Algebra beinhalten typische Beispiele einen Schritt, bei dem die Division durch Null auftritt, eine Wurzel falsch gezogen wird oder allgemeiner, wo unterschiedliche Werte einer mehrdeutigen Funktion gleichgesetzt werden. Bekannte Trugschlüsse sind auch in der Analysis und der euklidischen Geometrie bekannt. Ein berühmter Scheinbeweis basiert auf divergenten Reihen, aus denen fast jeder Unsinn abgeleitet werden kann.

Über die Geschichte der Trugschlüsse ist, von wenigen Ausnahmen abgesehen, wie die auf Trugschlüssen basierenden Paradoxien des Zenon von Elea, sehr wenig bekannt. Vielfach werden mathematische Scherze von Mund zu Mund verbreitet und erst später (meist ohne Namensangabe) irgendwo herausgegeben, ohne dass bekannt ist, ob das nun auch wirklich die erste Veröffentlichung ist.

Im Text sind

Trugschlüsse und Scheinbeweise

wie gezeigt in einem Kasten eingerahmt. Eine aufklappbares Textfeld „Auflösung [Ausklappen]“ im Kasten erläutert gegebenenfalls die List.

Arithmetik

Richtiges Ergebnis trotz falscher Rechnung

Eine eigene Klasse von Trugschlüssen (englisch howler ‚grober Schnitzer‘) entstehen durch eine korrekte Schlussfolgerung trotz fehlerhafter „Herleitung“. Manchmal gleichen sich zwei Fehler aus und erbringen das richtige Resultat. Solche fehlerhaften Argumente leiten nur in Spezialfällen zum richtigen Ergebnis, besitzen also keine Allgemeingültigkeit und sind mathematisch wertlos.

So kann jemand den Preis eines Einkaufs der in der Tabelle aufgeführten Waren

Menge	Ware	Einzelpreis	Mengeneinheit
¼ pf	Butter	2 s 10 d	pf
2½ pf	Schmalz	10 d	pf
3 pf	Zucker	3¼ d	pf
6 Schachteln	Streichhölzer	7 d	Dutzend = 12
4 Pakete	Seifen-Flocken	2½ d	Schachtel

durch einfaches Zusammenzählen der Einzelpreise zum – trotzdem – richtigen Endpreis summieren:

4 s 8¾ d	= 8½ d + 2 s 1 d + 9¾ d + 3½ d + 10 d
	= 2 s 10 d + 10 d + 3¼ d + 7 d + 2½ d

Das „Kürzen“ von Ziffern und Zeichen in einem Bruch belässt den Quotient nur in Ausnahmefällen unverändert:

${\frac {26}{65}}={\frac {26\!\!\!/}{6\!\!\!/5}}={\frac {2}{5}}$ oder gewagter ${\frac {a^{2}-b^{2}}{a-b}}={\frac {a^{2\!\!\backslash }{-\!\!\!\!/}\;b^{2\!\!\backslash }}{a\!\!\!\backslash -\!\!\!\!\!/\;b\!\!\!\backslash }}=a+b$

Das Herausziehen von Summanden aus einer Wurzel

${\sqrt {5{\frac {5}{24}}}}=5{\sqrt {\frac {5}{24}}}\quad {\text{oder}}\quad {\sqrt {12{\frac {12}{143}}}}=12{\sqrt {\frac {12}{143}}}$

ist normalerweise unzulässig, basiert hier aber auf der allgemeingültigen Regel

${\sqrt {n+{\frac {n}{n^{2}-1}}}}=n{\sqrt {\frac {n}{n^{2}-1}}}$

Verknüpfung von Gleichem mit Gleichem

Eine physikalische Größe besteht aus einem Zahlenwert und einer Maßeinheit. Wenn in Vorsätzen für die Maßeinheiten Faktoren versteckt sind aber nicht wie Faktoren behandelt werden, führt das leicht zu Trugschlüssen, beispielsweise:

2 kg = 2000 g

3 kg = 3000 g

Gleiches mit gleichem multipliziert ergibt Gleiches, also:

6 kg = 6 000 000 g = 6000 kg.

Auflösung

Wenn die Einheiten mitquadriert werden, kommt das richtige Ergebnis heraus: (3 kg) · (6 kg) = 18 kg² = (3000 g) · (6000 g) = 18 000 000 g² = 18 · (1000 g)² = 18 kg²

Lehrreich hieran ist, dass die Berücksichtigung der Einheiten in einer Rechnung ein Kriterium zu ihrer Überprüfung liefert. Am Ende der Rechnung müssen die Einheiten auf beiden Seiten einer Gleichung und in allen Summanden einer Summe übereinstimmen.

Das Zusammenwerfen von Äpfeln und Birnen führt auch mathematisch zu falschen Schlüssen:

Keine Katze hat acht Schwänze.

Eine Katze hat einen Schwanz mehr als keine Katze.

Gleiches zu Gleichem addiert ergibt Gleiches, also:

Eine Katze hat neun Schwänze.

Auflösung

Die „Nicht-Katze“ keine Katze im ersten Satz darf nicht mit den Katzen im zweiten Satz in einen Topf geworfen werden.

Algebra

Division durch 0

Aus der Identität 0 · a = 0 · b folgt nach Division durch den gemeinsamen Faktor 0 auf der rechten und linken Seite die Identität a = b, die nicht immer richtig sein muss. Diese unzulässige Division wird in den folgenden Beispielen durch Einführung von Variablen versteckt.

1) Es gelte	:  a = b
2) Multiplikation mit a	:  a² = a b
3) Addieren von a² - 2 a b	:  a² + ( a² - 2 a b ) = a b + ( a² - 2 a b )
4) Zusammenfassen	:  2 ( a² - a b ) = a² - a b
5) Eliminieren von a² - a b	:  2 = 1

Auflösung

Im fünften Schritt wird wegen a = b durch a² - a b = a ( a - b ) = 0 dividiert

In die Kategorie „mathematischer Witz“ gehört der Scheinbeweis von 1 + 1 = 2. Hier wird die Neigung von Mathematikern ausgenutzt, einen Satz, um seine Anwendbarkeit zu erweitern, möglichst allgemein zu formulieren und den Anlass der Untersuchung dann als Spezialfall einzuschließen.

Satz: 1 + 1 = 2

Beweis:

1) Ausgangspunkt	:  n ( 2n - 2 ) = n ( 2n - 2 )
2) Zusammenfassen	:  ( n - n ) ( 2n - 2 ) = 0
3) Vereinfachen	:  2n - 2 = 0
4) Umstellen	:  2n = 2
5) Umformen	:  n + n = 2

Mit n = 1 folgt die Behauptung, Q.e.d.

Auflösung

Im dritten Schritt wird durch n - n = 0 dividiert

Die Gleichung 1 + 1 = 2 als Spezialfall der „allgemeingültigen“ Gleichung n + n = 2 darzustellen, ist freilich absurd.

Gleichsetzen mehrdeutiger Ausdrücke

Eine Quadratzahl ungleich Null hat immer zwei verschiedene Wurzeln, eine positive und eine negative. Indem beide gleichgesetzt werden, können nach dem Schema ( -a )² = ( +a )² → -a = a erstaunliche Trugschlüsse „hergeleitet“ werden.

Satz: Alle Zahlen sind gleich

Beweisskizze: Wenn zwei beliebige Zahlen a und b immer gleich sind, dann sind alle Zahlen gleich.

1) Ausgangspunkt:	:  a + b = t mit beliebigem a und b
2) Multiplizieren mit ( a - b )	:  ( a - b )( a + b ) = ( a - b ) t
3) Ausmultiplizieren	:  a² - b² = a t - b t
4) Umstellen	:  a² - a t = b² - b t
5) Addieren von t²/4	:  a² - a t + t²/4 = b² - b t + t²/4
6) Zweite Binomische Formel	:  ( a - t/2 )² = ( b - t/2 )²
7) Vereinfachen	:  a - t/2 = b - t/2
8) Addieren von t/2	:  a = b
Q.e.d.

Auflösung

Im siebten Schritt werden die beiden verschiedenen Wurzeln eines Quadrats gleichgesetzt. Mit a - t/2 = -( b - t/2 ) ↔ a + b = t wäre der Trugschluss vermieden worden.

Im Reich der komplexen Zahlen hat jede Zahl zwei verschiedene Quadratwurzeln ( außer null ). Im Ausdruck ${\rm {i={\sqrt {-1}}}}$ steht der Ausdruck auf der rechten Seite also für zwei Werte +i und -i während links eine feste komplexe Zahl steht. Das kann Anlass zu Trugschlüssen sein.

1) Ausgangspunkt	:  ${\frac {-1}{1}}={\frac {1}{-1}}$
2) Wurzelziehen	:  ${\frac {\sqrt {-1}}{1}}={\frac {1}{\sqrt {-1}}}$
3) Einsetzen von i	:  ${\rm {i={\frac {1}{i}}}}$
4) Mit i multiplizieren	:  ${\rm {i^{2}=1}}$
5) i² = -1 einsetzen	:  $-1=1$

Auflösung

Im dritten Schritt werden die positve und die negative Wurzel aus -1 gleichgesetzt. Wird das nicht getan, wird der Widerspruch vermieden: ${\rm {i={\frac {1}{-i}}\quad \rightarrow \quad i^{2}={\frac {1}{-1}}=-1}}$ Das Potenzgesetz ( w/z )r = wr/zr ist im komplexen nur eingeschränkt gültig.

Auch die folgende Gleichungskette nutzt diese Tatsache aus:

$-1={\rm {i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)(-1)}}={\sqrt {1}}=1}}$

Auflösung

Beim mittleren Gleichheitsszeichen ${\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)(-1)}}$ wird auf der rechten Seite der übliche, positive Hauptwert der Wurzel im reellen benutzt. Hier führt aber nur der negative Wert zum richtigen Ergebnis $-1={\rm {i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}=-{\sqrt {(-1)(-1)}}=-{\sqrt {1}}=-1}}$. Das Potenzgesetz ( w · z )r = wr · zr ist im komplexen nur eingeschränkt gültig.

Nicht korrekter wird es, wenn i im Exponenten auftritt.

1) Eulersche Relation mit y = 2π	:  $e^{2\pi {\rm {i}}}=1$
2) Zur i-ten Potenz erheben	$\left(e^{2\pi {\rm {i}}}\right)^{\rm {i}}=1^{\rm {i}}$
3) Vereinfachen	:  $e^{-2\pi }=0{,}001867\ldots =1$

Auflösung

Im zweiten Schritt stehen links und rechts des Gleichheitsszeichens mehrdeutige Funktionen deren Werteberiche $\left\{z\in \mathbb {C} |z^{i}=\left(e^{2\pi {\rm {i}}}\right)^{\rm {i}}\right\}$ und $\{z\in \mathbb {C} |z^{\rm {i}}=1^{\rm {i}}\}$ gleich sind. Im dritten Schritt werden zwei ungleiche Elemente – die Hauptwerte der Potenzen – aus diesen Wertebereichen herausgepickt und gleichgesetzt, was zum Trugschluss führt. Das Potenzgesetz (za)b = za · b ist im komplexen nur eingeschränkt gültig.

Analysis

Differentialrechnung

In der Differentialrechnung werden Differentiale dx benutzt, die in bestimmten Fällen null sind, beispielsweise wenn x eine Konstante ist. Wie in der Algebra können daraus Trugschlüsse konstruiert werden.

Satz: Es gibt keinen Punkt auf einem Kreis, der zu einem anderen Punkt außerhalb des Kreisen am nächsten liegt.

Beweis über Differentialrechnung.

1) Gegeben ein Kreis mit Radius b um den Mittelpunkt M.

2) Sei P der Punkt, zu dem der nächste Punkt auf dem Kreis gesucht wird.

3) Der Einfachheit halber wird in den Punkt P der Ursprung eines kartesischen Koordinatensystems gelegt, dessen x-Achse durch den Mittelpunkt M geht. Die x-Koordinate von M sei a.

4) Für einen Punkt R = ( x, y ) auf dem Kreis gilt nach dem Satz von Pythagoras: ( x - a )² + y² = b² oder x² + y² - 2 a x + a² - b² = 0

5) Das Abstandsquadrat zwischen P und R ist nach Pythagoras r² := x² + y².

6) Mit 4) wird daraus: r² - 2 a x + a² - b² = 0.

7) Der Abstand PR ist extremal, wenn die Ableitung r'(x) = 0 ist.

8) Ableitung von 6) nach x resultiert in 2 r r' - 2 a = 0 oder r' = a/r, weil r ≠ 0.

9) Die Bedingung r' = 0 ist gemäß 8) nur erfüllt, wenn a = 0, das heißt P = M gilt.

10) Für alle Punkte außerhalb des Mittelpunkts des Kreises gibt es keinen nächsten Punkt auf dem Kreis.

Q.e.d.

Auflösung

Die Punkte R = ( x, y ) auf dem Kreis, die zum Ursprung des Koordinatensystems einen extremalen Abstand haben, liegen auf der x-Achse mit y = 0 und ( x - a )² = b². Das Differential von x erfüllt dort also 2 ( x - a ) dx = 0. Für einen Punkt auf dem Kreis und der x-Achse ist also dx = 0 wegen│ x - a │ = r ≠ 0. Das macht sich anschaulich dadurch bemerkbar, dass der Kreis die x-Achse senkrecht schneidet. Die für die Differentiation nach x notwendige Umgebung in x-Richtung existiert auf dem Kreis in diesen Schnittpunkten auf der x-Achse nicht, r'(x) kann im Extremum nicht berechnet werden, und alle aus r' = 0 gefolgerten Aussagen sind hinfällig. Der entscheidende Fehler wird also im dritten Schritt gemacht. Parametrisierung der Ebene mit Zylinderkoordinaten ( r, φ ), sodass ( x, y ) = ( r cos φ, r sin φ ) mit r = r(φ) ist, erlaubt die Gewinnung der dem Ursprung nächsten Punkte: r² - 2 a x + a² - b² = r² - 2 a r cos φ + a² - b² = 0 → 2 r r' - 2 a r' cos φ + 2 a r sin φ = 2 ( r - a cos φ ) r' + 2 a r sin φ = 0 Nun impliziert r' = 0 die Identität a r sin φ = 0 und daher sin φ = 0, solange der Kreis nicht durch P geht und somit r ≠ 0 ist. So sind die Punkte mit extremalem Abstand mit φ = 0° oder φ = 180° gefunden.

Integralrechnung

Bei der Ableitung einer Funktion f( x ) nach der Variablen x fallen alle von x unabhängigen Ausdrücke – insbesondere Konstanten – heraus. Umgekehrt ist die Stammfunktion – das unbestimmte Integral – nur bis auf eine Integrationskonstante bestimmt. So können nach dem Schema f₁'(x) = f₂'(x) → f₁(x) = f₂(x), was nicht immer richtig sein muss, Trugschlüsse konstruiert werden.

Satz: 0 = 1

Beweis über Partielle Integration:

1) Ausgangspunkt	:  $I=\int {\frac {1}{x\ln x}}\mathrm {d} x$  mit dem natürlichen Logarithmus ln.
2) Definition des ersten Faktors	:  $u=\ln x\quad \rightarrow \quad u'={\frac {1}{x}}$
3) Definition des zweiten Faktors	:  $v={\frac {1}{\ln x}}\quad \rightarrow \quad v'=-{\frac {1}{(\ln x)^{2}}}{\frac {1}{x}}=-{\frac {1}{x(\ln x)^{2}}}$
4) Einsetzen der Funktionen	:  $I=\int u'\cdot v\,\mathrm {d} x$
5) Partielle Integration	:  $I=u\cdot v-\int u\cdot v'\,\mathrm {d} x$
6) Ersetzen der Funktionen	:  $I=\ln x{\frac {1}{\ln x}}+\int \ln x\cdot {\frac {1}{x(\ln x)^{2}}}\,\mathrm {d} x$
7) Zusammenfassen	:  $I=1+\int {\frac {1}{x\ln x}}\,\mathrm {d} x$
8) Einsetzen von I	:  $I=1+I$
9) Subtrahieren von I	:  0 = 1
Q.e.d.

Auflösung

Im fünften Schritt, der partiellen Integration, wurden die Integrationsgrenzen in der Regel zur partiellen Integration gestrichen. Daher muss dort die Integrationskonstante C beachtet werden. Dann stünde in 8) I = 1 + I + C ohne Widerspruch. Siehe auch Partielle Integration#Unbestimmte Integrale und partielle Integration, wo im Unterabschnitt Kehrwertfunktion ein weiterer Trugschluss zu sehen ist.

Ableitungen aus divergenten Reihen

Mit divergenten Reihen kann (fast) alles „bewiesen“ werden. Ein berühmter Scheinbeweis behauptet, dass die Summe der natürlichen Zahlen minus ein zwölftel beträgt.

Gesucht ist der Wert der unendlichen Reihe

C = 1 + 2 + 3 + ...

Die Reihe C ist proportional zur unendlichen Reihe

B := 1 - 2 + 3 - 4 + 5 - 6 + - ...

denn:

C - B	= 1 + 2 + 3 + 4 + 5 + 6 + … - ( 1 - 2 + 3 - 4 + 5 - 6 + … )
	= ( 1 - 1 ) + ( 2 + 2 ) + ( 3 - 3 ) + ( 4 + 4 ) + ( 5 - 5 ) + ( 6 + 6 ) + …
	= 0 + 4 + 0 + 8 + 0 + 12 + ...
	= 4 · ( 1 + 2 + 3 + ... )
	= 4 · C
→ C	= - B/3

Die Reihe B lässt sich wie folgt abschätzen:

B + B	= 1 - 2 + 3 - 4 + 5 - 6 + ... + 1 - 2 + 3 - 4 + 5 - 6 + ...
	= 1 + 1 - 2 - 2 + 3 + 3 - 4 - 4 + 5 + 5 - 6 - 6 + ...
	= 1 + ( 1 - 2 ) + ( -2 + 3 ) + ( 3 - 4 ) + ( -4 + 5 ) + ( 5 - 6 ) - 6 + ...
	= 1 - 1 + 1 - 1 + 1 - 1 + ... =: A
→ B	= A/2

In der Reihe

A = 1 - 1 + 1 - 1 + 1 - 1 + ...

treten die Werte 0 und 1 wie beim Werfen einer perfekten Münze gleich oft auf und daher ist ½ der Erwartungswert der Reihe. Damit ist B = A/2 = ¼ und

C = 1 + 2 + 3 + … = -B/3 = -1/12

Q.e.d.

Auflösung

In der Herleitung ist fast alles falsch. Um das zu zeigen werden die n - ten Partialsummen, angezeigt durch den Index n, zunächst mit einem ungeraden n betrachtet. Dann ist $A_{n}=(1-1)+\dots +(1-1)+1=0+\dots +0+1=1$ und $B_{n}=\underbrace {(1-2)+(3-4)+\dots +(n-2-(n-1))} _{{\frac {n-1}{2}}\cdot (-1)={\frac {1-n}{2}}}+n={\frac {n+1}{2}}$ In der Summe ${\begin{aligned}B_{n}+B_{n}=&\underbrace {1+(1-2)+(-2+3)+\dots +(-(n-1)+n)} _{A_{n}}+n\\=&A_{n}+n\end{aligned}}$ entsteht noch ein „Rest“ n, was sich auch aus den Ausdrücken für An und Bn ergibt. Die Formel Bn = An/2 ist also in erster Ordnung von n falsch. Das reicht jedoch noch nicht, das in zweiter Ordnung falsche Endergebnis zu erklären. Die Differenz Cn - Bn der Parialsummen ergibt: ${\begin{aligned}C_{n}-B_{n}=&1+2+\dots +n-(1-2+-\dots +n)\\=&4\cdot \left(1+2+\dots +{\frac {n-1}{2}}\right)=4C_{(n-1)/2}\end{aligned}}$ Nach der Summenformel für Cn nähert sich das Verhältnis ${\frac {C_{n}}{C_{(n-1)/2}}}={\frac {{\frac {n}{2}}(n+1)}{{\frac {n-1}{4}}({\frac {n-1}{2}}+1)}}=4{\frac {n}{n-1}}$ mit wachsendem n der vier und weil Cn mit dem Quadrat von n zunimmt ist die Formel Cn = -Bn/3 in zweiter Ordnung falsch. Erst nach diesem Fehler wächst C nicht mehr quadratisch mit n an. Ausdrücken von C(n-1)/2 durch Cn bestätigt $C_{n}-B_{n}=4C_{(n-1)/2}={\frac {n-1}{n}}C_{n}\quad \rightarrow \quad C_{n}=nB_{n}={\frac {n}{2}}(n+1)$ Bei geradem n ist ${\begin{aligned}A_{n}=&0\\B_{n}=&-{\frac {n}{2}}\\2B_{n}=&A_{n}-n\\C_{n}-B_{n}=&4C_{n/2-1}+2n\end{aligned}}$ mit ähnlich vernichtendem Resultat.

Mit der Reihe A kann auch der Trugschluss

A	= 1 - 1 + 1 - 1 + ...	= 1 + ( -1 + 1 ) + ( -1 + 1 ) + …	= 1 + 0 + 0 + …	= 1
A	= 1 - 1 + 1 - 1 + ...	= ( 1 - 1 ) + ( 1 - 1 ) + ...	= 0 + 0 + …	= 0
→ 1	= 0

Auflösung

Der unbestimmt divergenten Reihe An kann für n → ∞ kein Wert zugewiesen werden. Der Vergleich zweier unbestimmter Werte ist mathematisch jedoch sinnlos.

konstruiert werden.

Logik

Vollständige Induktion

Die Vollständige Induktion ist eine mathematische Beweis­methode, nach der eine Aussage für alle natürlichen Zahlen bewiesen wird, die größer oder gleich einem bestimmten Startwert, beispielsweise 1, sind. Am Inuktionsanfang 1 trifft die Aussage oft offensichtlich zu. Dann wird im Induktionsschritt bewiesen, dass wenn die Aussage für n gilt (Induktionsvoraussetzung) sie auch für n + 1 gilt . Damit gilt sie dann für n = 1, daher auch für n = 2, daher auch für n = 3, usw. Bei inkorrekter Anwendung können Scheinbeweise wie der folgende auftreten.

Satz: Alle Deutschen haben dasselbe Alter.

Beweis über Vollständige Induktion:

Die Behauptung, dass in einer Gruppe von n Personen aus der Grundgesamtheit aller Deutschen alle dasselbe Alter haben, wird mit S(n) bezeichnet.

Induktionsanfang

In einer „Gruppe“ aus nur einer Person, sind alle Personen in der Gruppe gleichaltrig. Die Aussage S(1) trifft also jedenfalls zu.

Induktionsvoraussetzung

Sei die Behauptung S(n) für n ≥ 1 richtig. In einer Gruppe aus n Deutschen haben alle dasselbe Alter.

Induktionsschritt

Hier ist zu beweisen, dass wenn S(n) wahr ist, dies auch Gültigkeit von S(n + 1) nach sich zieht. Dazu werden n + 1 Deutsche in eine Reihe gestellt. Zunächst wird die erste Person P aus der Reihe genommen. Übrig bleiben n Deutsche in der Reihe, die nach Voraussetzung gleichaltrig sind. P wird wieder an erster Stelle der Reihe platziert und die letzte Person Q aus der Reihe entfernt. Übrig bleiben wieder n Deutsche, die nach Voraussetzung alle dasselbe Alter haben. Also haben alle Personen in der Reihe dasselbe Alter und die Behauptung S(n + 1) trifft zu.

Induktionsschluss

Damit ist S(n) für alle n bewiesen und alle Deutschen haben dasselbe Alter.

Auflösung

Das Problem ist hier der Schritt von n = 1 auf n + 1 = 2. Es gibt keine Person P, die gleichzeitig unter den letzten n und unter den ersten n Personen ist. Somit kann nicht geschlossen werden, dass weil die erste Person dasselbe Alter wie P hat und die letzte Person dasselbe Alter wie P hat, auch die erste und die letzte Person gleichaltrig sind. Für diesen Schluss bedarf es mindestens dreier Personen.

Faule Definitionen

Die Trugschlüsse im Bereich fauler Definitionen basieren auf dem logischen Konzept

Auf die Elemente der leeren Menge treffen alle Eigenschaften zu.

Das ist an sich eine vernünftige Vereinbarung, denn alle Mengen sind Erweiterungen der leeren Menge. Ein nicht-existentes Objekt kann aber für Trugschlüsse missbraucht werden, denn es hat dafür geeignete Eigenschaften.

So zum Beispiel die größte Natürliche Zahl.

Sei $N\in \mathbb {N} _{0}$ die größte natürliche Zahl, also N ≥ n für alle $n\in \mathbb {N} _{0}$. Insbesondere auch für n := N + 1 trifft das zu, weswegen N + 1 = n ≤ N folgt. Andererseits ist auch N ≥ 1 und N - 1 ≥ 0, weswegen $N-1\in \mathbb {N} _{0}$ und N - 1 ≤ N oder N ≤ N + 1 gilt. Damit ist N ≤ N + 1 ≤ N oder 0 ≤ 1 ≤ 0, was nur den Schluss 1 = 0 zulässt.

Auflösung

Alle Schlüsse sind unter der gemachten Prämisse korrekt. Weil diese jedoch widersprüchlich ist – eine größte natürliche Zahl gibt es nicht – kann über den Wahrheitsgehalt der gefundenen Ergebnisse nichts ausgesagt werden. Umgekehrt kann aus obiger Ableitung ein Beweis für die nicht-Existenz einer größten natürlichen Zahl gemacht werden.

Ein weiteres Beispiel zeigt, dass eine Erweiterung eines Zahlenbereichs mit Bedacht vorzunehmen ist.

Sei j die „imaginäre“ Zahl für die 0 · j = 1 gilt.

Dann ist 1 = 0 · j = ( 0 + 0 ) · j = 0 · j + 0 · j = 1 + 1 = 2

oder 0 = 1.

Trugschlüsse in der Geometrie

In der Geometrie können Trugschlüsse hinter ungenau gezeichneten Skizzen versteckt werden. Die in den Skizzen gezeigten geometrischen Verhältnisse können bei genauer Betrachtung gar nicht auftreten. Der Gutgläubige wird so zum Trugschluss geleitet.

Satz: Alle Punkte innerhalb eines Kreises liegen auf seinem Umfang.

Beweis: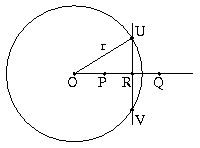
1) Gegeben sei ein Kreis um O und Radius r wie im Bild.
2) Gegeben sei ein Punkt P ≠ O innerhalb des Kreises.
3) Sei Q der Punkt auf der Halbgeraden [OP), für den gilt OP · OQ = r²
4) Die Mittelsenkrechte von [PQ] schneide (PQ) in R und den Kreis in einem Punkt U.
5) Dann ist mit 3) r² = OP · OQ = ( OR - RP ) · ( OR + RP ) = OR² - RP²
6) Mit dem Satz von Pythagoras ist OR² = r² - RU² und PR² = PU² - RU²
7) Nun 6) in 5) eingesetzt ergibt: r² = ( r² - RU² ) - ( PU² - RU² ) = r² - PU²
8) Also ist PU = 0
Q.e.d.

Auflösung

Der Punkt R liegt, anders als in der Skizze, außerhalb des Kreises, weswegen es den Schnittpunkt U nicht gibt. Das folgt mit den Voraussetzungen OP · OQ = r² und 2 OR = OP + OQ aus 0 < ( r - OP )² = r² - 2 r · OP + OP² → 2 r · OP < r² + OP² = OQ · OP + OP² = ( OQ + OP ) · OP = 2 OR · OP → r < OR. Der entscheidende Fehler wird also im vierten Schritt gemacht, wo ein Schnittpunkt U unterstellt wird, den es nicht geben kann.

Die folgenden Zerlegungen sind weitere Beispiele.

Skizze zum Scheinbeweis von 64 = 65.	Skizze zum Scheinbeweis von 216 = 217.

Satz: 64 = 65 und 216 = 217.

Beweis durch Zerlegungen:

Das Quadrat im linken Bild hat die Fläche 8 · 8 = 64 und wird in zwei Dreiecke und zwei Vierecke zerlegt. Aus diesen kann das Rechteck unter dem Quadrat zusammengesetzt werden, das den Flächeninhalt 5 · 13 = 65 hat.

Das obere Rechteck im rechten Bild hat die Fläche 9 · 24 = 216 und wird in zwei Dreiecke und zwei Vierecke zerlegt. Aus diesen kann das Rechteck darunter zusammengesetzt werden, das den Flächeninhalt 7 · 31 = 217 hat.

Q.e.d.

Auflösung

Die Diagonalen in den unteren Rechtecken sind nur scheinbar gerade. Würden die Teilstücke unverformt zusammengesetzt, würden sich die Teile auf einer Fläche überschneiden, die genau den Inhalt einer Flächeneinheit hat. Beweisen lässt sich das mit dem Strahlensatz. Im zum Quadrat gehörenden Rechteck sollte auf der Diagonalen ${\frac {5}{13}}={\frac {3}{8}}={\frac {2}{5}}\quad \Leftrightarrow \quad {\frac {200}{520}}={\frac {195}{520}}={\frac {208}{520}}$ sein, was offensichtlich nicht zutrifft. Im rechten unteren Rechteck sollte ${\frac {7}{31}}={\frac {5}{22}}={\frac {2}{9}}\quad \Leftrightarrow \quad {\frac {1386}{6138}}={\frac {1395}{6138}}={\frac {1364}{6138}}$ sein, was ebenfalls nicht zutrifft.

Für die linke Zerlegung sind aufeinander folgende Zahlen f_n-1, f_n, f_n+1 der Fibonacci-Folge geeignet, denn bei ihnen gilt die Identität von Cassini f_n+1 f_n-1 = (f_n)² + (-1)ⁿ. Für die Zerlegung der Rechtecke im rechten Bild eignen sich zwei aufeinander folgende Näherungswerte eines beliebigen Kettenbruchs.

Fehlerhafte Annahmen

In der realen Welt sind alle Körper mehr oder weniger verformbar und Zwangsbedingungen immer mehr oder weniger flexibel, was Kräfte und/oder Beschleunigungen auf endliche Werte begrenzt. Die Berechnung flexibler Systeme kann durch vereinfachende Annahmen wesentlich erleichtert werden. Ein in diesem Sinn erfolgreiches Modell der klassischen Mechanik ist der unverformbare Starrkörper. Wird dieser weiteren Zwangsbedingungen unterworfen, können schnell unrealistische Unendlichkeiten auftreten. Die fallende Leiter ist ein Beispiel dafür.

Die Leiter im Bild lehnt an einer Wand und steht auf dem Boden, wobei ihr Fußpunkt mit konstanter Geschwindigkeit von der Wand weggezogen wird. Dann schlägt die Leiter mit unendlicher Geschwindigkeit auf dem Boden auf.

Beweis:

1) Definition	:	Die Leiter habe die Länge L.	An Wand und Boden (schwarz) anlehnende Leiter (blau)
2) Definition	:	Sei $x$ der horizonale Abstand der Wand vom Fußpunkt der Leiter, der mit konstanter Geschwindigkeit $v$ von der Wand weggezogen wird.
3) Definition	:	Sei $y$ der vertikale Abstand des Bodens vom Berührungspunkt der Leiter mit der Wand.
4) Satz von Pythagoras	:	$x^{2}+y^{2}=L^{2}\quad \rightarrow \quad y={\sqrt {L^{2}-x^{2}}}$
5) Zeitableitung	:	${\dot {y}}=-{\frac {x{\dot {x}}}{\sqrt {L^{2}-x^{2}}}}$
6) Einsetzen der Geschwindigkeit	:	${\dot {y}}=-{\frac {xv}{\sqrt {L^{2}-x^{2}}}}$
7) Beim Aufschlagen	:	$\lim _{x\to L}{\dot {y}}=\lim _{x\to L}{\frac {-xv}{\sqrt {L^{2}-x^{2}}}}=-\infty$

Deshalb schlägt die Leiter mit unendlich hoher Geschwindigkeit auf dem Boden auf.

Auflösung

Die Ursache dieses Trugschlusses ist die Annahme in 4), dass die Leiter an der Wand gelehnt bleibt und sie immer berührt. Tatsächlich wird der Zug am Fuß der Leiter auch das obere Ende der Leiter von der Wand wegziehen, so dass der Kontakt aufhört und der Satz von Pythagoras nicht mehr gilt.

Weblinks

• Mathematik Witze. (html) Abgerufen am 2. Juli 2017. 
• Math jokes. (html) Aha! Jokes LLC, abgerufen am 2. Juli 2017 (englisch). 
• Prof. Uwe Stephan. (html) Abgerufen am 2. Juli 2017. 

Literatur

• Underwood Dudley: Mathematik Zwischen Wahn und Witz: Trugschlüsse, Falsche Beweise und die Bedeutung der Zahl 57 für die Amerikanische Geschichte. Birkhäuser Verlag, 1995, ISBN 978-3-7643-5145-8.