Satz des Pythagoras
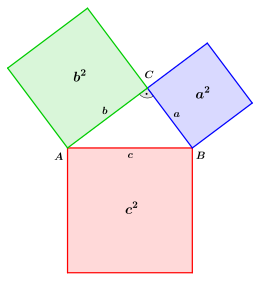
Der Satz des Pythagoras (auch Hypotenusensatz)[1] ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Sind und die Längen der am rechten Winkel anliegenden Seiten, der Katheten, und die Länge der dem rechten Winkel gegenüberliegenden Seite, der Hypotenuse, dann lautet der Satz als Gleichung ausgedrückt:
Der Satz ist nach Pythagoras von Samos benannt, der als Erster dafür einen mathematischen Beweis gefunden haben soll, was allerdings in der Forschung umstritten ist. Die Aussage des Satzes war schon lange vor der Zeit des Pythagoras in Babylon und Indien bekannt, es gibt jedoch keinen Nachweis dafür, dass man dort auch einen Beweis hatte.
Mathematische Aussage
Der Satz des Pythagoras lässt sich folgendermaßen formulieren:
- Sind , und die Seitenlängen eines rechtwinkligen Dreiecks, wobei und die Längen der Katheten sind und die Länge der Hypotenuse ist, so gilt .
In geometrischer Deutung ist demnach in einem rechtwinkligen Dreieck die Summe der Flächen der beiden Quadrate über den Katheten gleich der Fläche des Quadrats über der Hypotenuse.
Die Umkehrung des Satzes gilt ebenso:
- Gilt die Gleichung in einem Dreieck mit den Seitenlängen , und , so ist dieses Dreieck rechtwinklig, wobei der rechte Winkel der Seite gegenüberliegt.
Eng verwandt mit dem Satz des Pythagoras sind der Höhensatz und der Kathetensatz. Diese beiden Sätze und der Satz des Pythagoras bilden zusammen die Satzgruppe des Pythagoras. Der unten beschriebene Kosinussatz ist eine Verallgemeinerung des pythagoreischen Satzes.
Verwendung
Längen im rechtwinkligen Dreieck
Aus dem Satz des Pythagoras folgt direkt, dass die Länge der Hypotenuse gleich der Quadratwurzel aus der Summe der Kathetenquadrate ist, also
- .
Eine einfache und wichtige Anwendung des Satzes ist, aus zwei bekannten Seiten eines rechtwinkligen Dreiecks die dritte zu berechnen. Dies ist durch Umformung der Gleichung für alle Seiten möglich:
Die Umkehrung des Satzes kann dazu verwendet werden, zu überprüfen, ob ein gegebenes Dreieck rechtwinklig ist. Dazu wird getestet, ob die Gleichung des Satzes für die Seiten bei dem gegebenen Dreieck zutrifft. Es reicht also allein die Kenntnis der Seitenlängen eines gegebenen Dreiecks, um daraus zu schließen, ob es rechtwinklig ist oder nicht:
- Sind die Seitenlängen z. B. , und , dann ergibt sich , und daher ist das Dreieck rechtwinklig.
- Sind die Seitenlängen z. B. , und , dann ergibt sich , und daher ist das Dreieck nicht rechtwinklig.
Aus dem Satz des Pythagoras folgt, dass in einem rechtwinkligen Dreieck die Hypotenuse länger als jede der Katheten und kürzer als deren Summe ist. Letzteres ergibt sich auch aus der Dreiecksungleichung.
Reziproke Längen im rechtwinkligen Dreieck

Aus dem Satz des Pythagoras folgt als direkte Anwendung der reziproke Satz des Pythagoras:
Sind und die Längen der Katheten und die Länge der Höhe auf der Hypotenuse in einem rechtwinkligen Dreieck , dann sind und die Kathetenlängen und die Hypotenusenlänge eines zu ähnlichen rechtwinkligen Dreiecks .
Somit folgt: .
Wegen der Rechtwinkligkeit gilt für die Flächenmaßzahl des Dreiecks ABC die Gleichheit oder .
Durch Division der Pythagorasgleichung auf beiden Seiten durch und Einsetzen von für ergibt sich die Aussage des Satzes aus folgender Äquivalenzkette:
Pythagoreische Tripel
Unter allen Dreiergruppen , die die Gleichung erfüllen, gibt es unendlich viele, bei denen , und jeweils ganze Zahlen sind. Diese Dreiergruppen werden pythagoreische Tripel genannt. Das einfachste dieser Tripel besteht aus den Zahlen , und . Pythagoreische Tripel werden seit alters her zur Konstruktion rechtwinkliger Dreiecke verwendet. Ein Beispiel ist die Zwölfknotenschnur, mit der ein Dreieck gelegt wird, dessen Seiten die Längen , und haben. Die beiden kurzen Seiten bilden dann einen rechten Winkel.
Der große fermatsche Satz besagt, dass die -te Potenz einer Zahl, wenn ist, nicht als Summe zweier Potenzen des gleichen Grades dargestellt werden kann. Gemeint sind ganze Grundzahlen und natürliche Hochzahlen. Allgemein gesprochen bedeutet dies:
- Die Gleichung besitzt für ganzzahlige und natürliche Zahlen keine Lösung.
Das ist erstaunlich, weil es für unendlich viele Lösungen gibt. Für sind dies die pythagoreischen Zahlentripel.
Trotz seiner einfachen Formulierung gilt der Beweis des großen fermatschen Satzes, der erst 1995 erbracht werden konnte, als außerordentlich schwierig.
Euklidischer Abstand
Der Satz von Pythagoras liefert eine Formel für den Abstand zweier Punkte in einem kartesischen Koordinatensystem. Sind zwei Punkte und in einer Ebene gegeben, dann ist ihr Abstand durch
gegeben. Hierbei wird ausgenutzt, dass die Koordinatenachsen senkrecht zueinander liegen. Diese Formel kann auch auf mehr als zwei Dimensionen erweitert werden und liefert dann den euklidischen Abstand. Zum Beispiel gilt im dreidimensionalen euklidischen Raum
- .
Das entspricht auch dem Betrag bzw. der Länge des durch die beiden Punkte definierten Vektors.
Beweise
Für den Satz sind mehrere hundert Beweise bekannt,[3] womit er wohl der meistbewiesene mathematische Satz ist. Elisha Scott Loomis führt in einem zuerst 1927 erschienenen Buch 371 Beweise auf.[4][5] Mario Gerwig[6] führt in einer Überarbeitung und Ergänzung der Loomis-Sammlung rund 365 verschiedene Beweise auf, wobei er Loomis rund 360 Beweise zuordnet und eine ganze Reihe von Fehlern, darunter auch der Aufnahme offensichtlich falscher Beweise. Exemplarisch werden im Folgenden sechs geometrische Beweise vorgestellt. Ein siebter Beweis aus dem Jahr 1875 von James A. Garfield findet sich unter Beweis des Satzes des Pythagoras nach Garfield, der dem Beweis durch Ergänzung stark ähnelt.
Beweis nach Euklid

Euklid beschreibt den Satz des Pythagoras mit dem folgenden Beweis im ersten Buch seiner Elemente in der Proposition 47.[7] Dort beweist er zunächst den Kathetensatz mit Hilfe kongruenter Dreiecke, aus welchem dann unmittelbar der Satz des Pythagoras folgt. Der Beweis benutzt nicht die Theorie der Proportionen, die Euklid im Buch 5 der Elemente entwickelt, sondern kommt allein mit den Sätzen des ersten Buches der Elemente aus und ist von konstruktiver Natur.
Für ein Dreieck mit rechtem Winkel in sind und die Quadrate über den Katheten und der Fußpunkt der Höhe von auf . Des Weiteren sind und Rechtecke über der Hypotenuse deren längere Seite die Länge der Seite besitzt. Nun sind die Dreiecke und nach dem zweiten Kongruenzsatz (SWS) kongruent, da , und gilt. Zudem gilt, dass die Fläche des Dreiecks die Hälfte der Fläche des Rechtecks beträgt, da dessen Grundseite und die Rechteckseite gleich lang sind und die Länge seiner Höhe von der Länge der anderen Rechteckseite entspricht. Aufgrund eines entsprechenden Arguments folgt, dass die Fläche des Dreiecks der Hälfte der Fläche des Kathetenquadrates entspricht. Wegen der Kongruenz der Dreiecke und bedeutet dies aber, dass dann auch das Kathetenquadrat flächengleich mit dem Rechteck ist. Analog lässt sich mit Hilfe der kongruenten Dreiecke und zeigen, dass das zweite Kathetenquadrat flächengleich mit dem Rechteck ist. Damit hat man den Kathetensatz bewiesen. Der Satz des Pythagoras folgt dann sofort, da das Hypotenusenquadrat sich aus den Rechtecken und zusammensetzt.
Es gibt noch einen weiteren Beweis des Satzes von Pythagoras in den Elementen in Buch 6, Proposition 31 (siehe unten).[8] Er benutzt statt Quadraten zueinander ähnliche Rechtecke auf den drei Seiten, ist formal einfacher als der Beweis im ersten Buch durch Verwendung der Theorie der Proportionen, die erst von Eudoxos von Knidos streng begründet wurde. Pythagoras kann beide Beweise aller Wahrscheinlichkeit nach nicht gekannt haben, da sie einem fortgeschritteneren Verständnis der Geometrie entsprechen[9] Proklos schrieb die Beweise in seinem Kommentar zu den Elementen explizit Euklid zu und drückte seine Bewunderung für beide Beweise aus.
Euklid gibt in der letzten Proposition 48 von Buch 1 zusätzlich eine Umkehrung des Satzes von Pythagoras, indem er zeigt, dass aus der Gleichheit der Fläche des Hypotenusenquadrats mit der der Summe der Kathetenquadrate folgt, dass einer der Winkel des Dreiecks ein rechter Winkel ist.[10]
Der erste Beweis (I, 47) wird wegen der Form der Hilfslinien in der zugehörigen Figur im englischen Sprachraum gelegentlich auch windmill (Windmühle) genannt,[11][12] Arthur Schopenhauer nahm den ersten Beweis von Euklid als Beispiel für dessen in seiner Sicht willkürliche und wenig anschauliche Vorgehensweise („Oft werden, wie im Pythagoreischen Lehrsatze, Linien gezogen, ohne dass man weiss warum: hinterher zeigt sich,dass es Schlingen waren, die sich unerwartet zuziehen“, und so die Zustimmung Lernenden erzwingen, „der nun verwundert zugeben muß , was ihm seinem inneren Zusammenhang nach völlig unbegreiflich bleibt“)[13] Felix Klein verteidigte den Beweis dagegen in einer Erwiderung auf Schopenhauers Kritik als besonders anschaulich und demonstrierte dies in seiner Elementarmathematik vom höheren Standpunkt.[14]
Beweis durch Addition abgeleiteter Flächeninhalte
Der in den beiden nebenstehenden Bildern auf unterschiedlicher Weise verdeutlichte Beweis durch Addition abgeleiteter Flächeninhalte,[15] stammt aus dem chinesischen Werk Zhoubi suanjing, übersetzt Klassische Arithmetik des Gnomon und die Kreisbahnen des Himmels (es wird heute angenommen, das Werk „stamme frühestens aus dem späten 4. Jahrhundert v. Chr.“).[16] Darin kommt das allgemein bekannte rechtwinklige Dreieck mit den Seiten und zur Anwendung.
Nach dem Zeichnen eines Quadrats (Bild 1) und dessen Unterteilung in x Einheitsquadrate, wird das rechtwinklige Ausgangsdreieck (rot) mit den Katheten , und mit der sich ergebenden Hypotenuse anhand des Gitters eingetragen. Darüber hinaus werden drei, dem Ausgangsdreieck gleichende Dreiecke so platziert, dass die Hypotenusen ein inneres Quadrat ergeben und demzufolge ein zentrales Einheitsquadrat (gelb) mit dem Flächeninhalt umgrenzen. Ein auf das innere Quadrat eingezeichnetes Gitter, das dem äußeren gleicht und mit den Hypotenusen einen rechten Winkel einschließt, liefert x Einheitsquadrate.
Der Flächeninhalt des inneren Quadrats mit den vier Dreiecken und dem zentralen Einheitsquadrat entspricht Einheitsquadraten. Die gesamte Anzahl der (gelben) Einheitsquadrate ergibt sich aus den Einheitsquadraten des äußeren Quadrats abzüglich der vier Dreiecksflächen des inneren Quadrats; dies bringt ebenfalls Einheitsquadrate.
Die Seitenlänge des inneren Quadrats ist die Hypotenuse somit gilt als allgemeine Formel
Werte für und eingesetzt:
- (Flächeneinheiten)
- (Längeneinheiten)
Die Animation (Bild 2) verdeutlicht dies auf vergleichbarer Art und Weise.
Beweis durch Ergänzung

In ein Quadrat mit der Seitenlänge werden vier kongruente rechtwinklige Dreiecke mit den Seiten , und (Hypotenuse) eingelegt. Dies kann auf zwei Arten geschehen, wie im Diagramm dargestellt ist.
Die Flächen des linken und des rechten Quadrates sind gleich (Seitenlänge ). Das linke besteht aus den vier rechtwinkligen Dreiecken und einem Quadrat mit Seitenlänge , das rechte aus den gleichen Dreiecken sowie einem Quadrat mit Seitenlänge und einem mit Seitenlänge . Die Fläche entspricht also der Summe der Fläche und der Fläche , also
- .
Eine algebraische Lösung ergibt sich aus dem linken Bild des Diagramms. Das große Quadrat hat die Seitenlänge und somit die Fläche . Zieht man von dieser Fläche die vier Dreiecke ab, die jeweils eine Fläche von (also insgesamt ) haben, so bleibt die Fläche übrig. Es ist also
- .
Auflösen der Klammer liefert
- .
Zieht man nun auf beiden Seiten ab, bleibt der Satz des Pythagoras übrig.
Beweis durch Scherung

Eine Möglichkeit ist die Scherung der Kathetenquadrate in das Hypotenusenquadrat. Unter Scherung eines Rechtecks versteht man in der Geometrie die Überführung des Rechtecks in ein Parallelogramm unter Beibehaltung der Höhe. Bei der Scherung ist das sich ergebende Parallelogramm zu dem Ausgangsrechteck flächengleich. Über zwei Scherungen können die beiden kleineren Quadrate dann in zwei Rechtecke umgewandelt werden, die zusammen genau in das große Quadrat passen.
Beim exakten Beweis muss dann noch über die Kongruenzsätze im Dreieck nachgewiesen werden, dass die kleinere Seite der sich ergebenden Rechtecke jeweils dem betreffenden Hypotenusenabschnitt entspricht. Wie üblich wurden in der Animation die Höhe mit und die Hypotenusenabschnitte mit bezeichnet.
Beweis durch Parkettierung
Die gesamte Ebene lässt sich mit zwei verschiedenen Sorten von jeweils flächengleichen Quadraten parkettieren. Jedes der grünen Quadrate habe den Flächeninhalt , jedes der gelben Quadrate den Flächeninhalt und jedes der rot umrandeten Quadrate den Flächeninhalt .
Da einerseits die grünen und die gelben Quadrate zusammen und andererseits die rot umrandeten Quadrate jeweils die gesamte Ebene parkettieren, muss gelten.[17]
Figur 1 zeigt die Parkettierung mit Kathetenquadraten (grün und gelb) bzw. mit Hypotenusenquadraten (rot umrandet). In Figur 2 ist in einem Parkettierungsausschnitt die Pythagorasfigur eingezeichnet. Das an der Kathete gespiegelte grüne Kathetenquadrat ist gestrichelt als Teil der Parkettierung eingezeichnet.
Beweis mit Ähnlichkeiten

Es ist nicht unbedingt notwendig, zum Beweis des Satzes von Pythagoras (explizit) Flächen heranzuziehen. Geometrisch eleganter ist es, Ähnlichkeiten zu verwenden. Sobald man sich durch Berechnung der Winkelsummen im Dreieck überzeugt hat, dass die beiden Winkel im unteren Bild gleich groß sein müssen, sieht man, dass die Dreiecke , und ähnlich sind. Der Beweis des Satzes von Pythagoras ergibt sich dann wie im Bild gezeigt, dabei beweist man auch den Kathetensatz und die Addition beider Varianten des Kathetensatzes ergibt den Satz des Pythagoras selbst. Diese Herleitung lässt sich anschaulich mit der Ähnlichkeit der Quadrate und der Ähnlichkeit deren angrenzenden Dreiecke erklären. Da deren Fläche proportional zur Fläche der jeweils anliegenden Quadrate ist, repräsentiert die Gleichung
den Satz: Die Flächen der Dreiecke CBD, ACD und ABC sind wegen Ähnlichkeit proportional zu den Quadraten über den Kanten und bestimmen sich daher zu q·a2, q·b2 und q·c2 mit einem unbekannten Faktor q ungleich Null. Das sich die ersten beiden zum dritten, vollen Dreieck ergänzen, gilt
- q·a2 + q·b2 = q·c2.
Da q von Null verschieden ist, können wir diese Gleichung auf beiden Seiten durch q teilen und erhalten die gewünschte Beziehung. Es ist also gar nicht nötig, q zu berechnen, was die Beweisführung stark vereinfacht. Diesen bis dahin offenbar unbekannten Beweis soll Albert Einstein im Alter von zwölf Jahren gefunden haben.[18]
Ebenso kann in der Figur rechts eine Parallele zu AB von der Höhe h auf die Seite a gezogen werden, was weitere ähnliche Dreiecke und unendlich viele Beweismöglichkeiten liefert.[19]
Beweis der Umkehrung

Links: Gewähltes Ausgangsdreieck erfüllt
Rechts: Rechtwinkliges Dreieck, dessen Längen der Katheten entsprechen den Seitenlängen von und des Ausgangsdreiecks
Die Umkehrung des Satzes lässt sich auf verschiedene Arten beweisen, ein besonders einfacher Beweis ergibt sich jedoch, wenn man den Satz des Pythagoras selbst zum Beweis seiner Umkehrung heranzieht.
Zu einem beliebigen Dreieck, dessen Seiten die Bedingung erfüllen, konstruiert man ein zweites Dreieck. Dieses besitzt einen rechten Winkel, dessen Schenkellängen den Seitenlängen von und entsprechen. Nach dem Satz des Pythagoras beträgt nun die Länge der Hypotenuse in diesem zweiten Dreieck und entspricht damit der Länge der Seite des Ausgangsdreiecks. Somit besitzen die beiden Dreiecke die gleichen Seitenlängen und sind aufgrund des ersten Kongruenzsatzes (SSS) kongruent. Damit sind dann aber auch ihre Winkel gleich, das heißt, auch das Ausgangsdreieck besitzt einen rechten Winkel, der der Seite gegenüberliegt.
Verallgemeinerungen und Abgrenzung
Kosinussatz
Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras für beliebige Dreiecke:
- ,
wobei der Winkel zwischen den Seiten und ist. Der Kosinussatz unterscheidet sich also durch den Term vom Satz des Pythagoras. Da der Kosinus von gleich null ist, fällt dieser Term bei einem rechten Winkel weg, und es ergibt sich als Spezialfall der Satz des Pythagoras. Gilt umgekehrt in einem Dreieck die Beziehung
- ,
so muss sein, woraus folgt, und daher ist das Dreieck rechtwinklig. Für spitzwinklige Dreiecke gilt entsprechend
und für stumpfwinklige Dreiecke
- .
Verallgemeinerung von Thabit ibn Qurra

Gleichfarbige Rechtecke sind flächengleich,
gleichfarbige Winkel sind gleich groß,
Eine auf Thabit ibn Qurra zurückgehende Verallgemeinerung liefert zu den Quadraten über zwei Seiten eines beliebigen Dreiecks ein Rechteck über der dritten Seite, dessen Fläche der Summe der beiden Quadratflächen entspricht.[20]
Zu einem beliebigen Dreieck mit Seiten , Winkel in und Höhe konstruiert man ein gleichschenkliges Dreieck dessen Basis auf der Seite liegt und das als Höhe besitzt. Darüber hinaus besitzen seine beiden Basiswinkel die gleiche Größe wie , sofern ein spitzer Winkel ist. Ist hingegen ein stumpfer Winkel, so sollen die Basiswinkel betragen. Ferner wird der Eckpunkt des gleichschenkligen Dreiecks, der auf derselben Seite von wie liegt, mit bezeichnet und der andere Eckpunkt auf derselben Seite wie mit . Dies gilt jedoch nur im Falle , für vertauscht man stattdessen und . Im Fall fällt das gleichschenklige Dreieck mit der Höhe zusammen und die Punkte und dementsprechend mit dem Punkt . Definiert man nun und , so gilt:
Für gilt dabei und die obige Gleichung liefert den Satz des Pythagoras.
Die Aussage lässt sich analog zum Satz des Pythagoras direkt über ähnliche Dreiecke beweisen, wobei hier die Dreiecke , und ähnlich sind.[21][22]
Aufgrund von
liefert Qurras Verallgemeinerung auch eine geometrische Darstellung des Korrekturterms im Kosinussatz als ein Rechteck, das zu dem Quadrat über der Seite hinzugefügt oder von ihm abgetrennt wird, um eine Fläche zu erhalten, die der Summe der Flächen der Quadrate über den Seiten und entspricht.
Flächensatz von Pappus

Eine weitere Verallgemeinerung auf beliebige Dreiecke liefert die Flächenformel von Pappus. Hier ergibt sich aus zwei beliebigen Parallelogrammen über zwei Seiten eines beliebigen Dreiecks ein eindeutig bestimmtes Parallelogramm über der dritten Seite des Dreiecks, dessen Fläche der Summe der Flächen der beiden Ausgangsparallelogramme entspricht. Sind die beiden Ausgangsparallelogramme Quadrate, so erhält man im Falle eines rechtwinkligen Dreiecks ein Quadrat über der dritten Seite und damit den Satz des Pythagoras.
Das Parallelogramm über der dritten Seiten erhält man, indem man die beiden Seiten der Ausgangsparallelogramme, die parallel zu den Dreiecksseiten sind, verlängert und deren Schnittpunkt mit dem Eckpunkt des Dreiecks, der auch auf beiden Parallelogrammen liegt, verbindet. Diese Verbindungsstrecke liefert das zweite Seitenpaar des Parallelogramms über der dritten Seite (siehe Zeichnung).[23][24]
Ähnliche Figuren, errichtet über den Seiten des rechtwinkligen Dreiecks

Es gilt:

Es gilt jeweils:
Eine Verallgemeinerung des Satzes des Pythagoras mithilfe von drei zueinander ähnlichen Figuren über den Dreieckseiten (neben den bereits bekannten Quadraten) war bereits Hippokrates von Chios im 5. Jahrhundert v. Chr. bekannt[25][26] und wurde, wahrscheinlich zweihundert Jahre später, von Euklid in seinem Werk Elemente aufgenommen:
„Im rechtwinkligen Dreieck ist die gradlinige Figur über der Hypotenuse gleich den ähnlichen und ähnlich errichteten Figuren über den Katheten zusammen.“
Errichtet man über den drei Seiten und des ursprünglichen Dreiecks jeweils eine zu den beiden anderen ähnliche Figur (Bild 1) mit den Flächen und dann gilt wegen ihrer Ähnlichkeit:
Stellt man und in der Form
dar, so erhält man für die Summe:
Nach dem Satz des Pythagoras wird für eingesetzt und somit ergibt sich:
Während Euklids Beweis nur für konvexe Polygone (Vielecke) gilt,[27] ist der Satz auch für konkave Polygone und sogar für ähnliche Figuren mit gekrümmten Grenzen gültig, wobei auch diese Figuren aus einer betreffenden Seite des ursprünglichen Dreiecks hervorgehen.[25] Die im Bild 2 dargestellten Flächen und der Kreise entstehen aus den Seiten und der Fünfecke.
Um zu verdeutlichen, dass Kreise bzw. Halbkreise[28] allein, d. h. ohne Vielecke über den Seiten, zur Verallgemeinerung herangezogen werden können, erweitert man den Satz des Pythagoras mit der Kreiszahl
Aus dem Satz mit Quadraten
wird, mit den entsprechenden Seitenlängen und als Radien, eine Verallgemeinerung mit Kreisen
bzw. eine Verallgemeinerung mit Halbkreisen:
Die Grundidee hinter dieser Verallgemeinerung ist, dass die Fläche einer ebenen Figur proportional zum Quadrat jeder linearen Dimension und insbesondere proportional zum Quadrat der Länge jeder Seite ist.
Skalarprodukträume
Abstrahiert man vom gewöhnlichen euklidischen Raum zu allgemeinen Skalarprodukträumen, also Vektorräumen mit einem Skalarprodukt, dann gilt:
Sind zwei Vektoren und zueinander orthogonal, ist also ihr Skalarprodukt , dann gilt aufgrund der Linearität des Skalarprodukts
- ,
wobei die von dem Skalarprodukt induzierte Norm bezeichnet.
Bezieht man diesen Satz wiederum auf den euklidischen Raum, dann stehen und für die Katheten und eines rechtwinkligen Dreiecks. steht für die Länge der Hypotenuse .
Diese Verallgemeinerung des Satzes des Pythagoras findet sich auch in abstrakten mathematischen Strukturen, etwa unendlichdimensionalen Funktionenräumen wieder. Die Umkehrung gilt ebenfalls. Trifft die Gleichung zu, so sind die beiden Vektoren orthogonal zueinander. Der Satz lässt sich noch weiter verallgemeinern. Ist ein Orthogonalsystem bestehend aus paarweise orthogonalen Vektoren , dann folgt durch wiederholte Anwendung obigen Arguments:
Die entsprechende Aussage gilt sogar für unendliche Summen, wenn man eine Folge von Vektoren betrachtet, die alle zueinander orthogonal sind. Konvergiert nun die Reihe , so konvergiert auch und es gilt:
Der Beweis der zweiten Behauptung folgt dabei aus der Stetigkeit des Skalarprodukts. Eine weitere Verallgemeinerung führt zur Parsevalschen Gleichung.
Weitere Verallgemeinerungen
Ebenfalls als Verallgemeinerungen des Satzes des Pythagoras können der Schenkeltransversalensatz, der Satz von Stewart, der Satz von Ptolemäus, der Satz von Carnot über Lote am Dreieck und der Satz von der britischen Flagge gelten. Letzterer stellt sowohl eine Verallgemeinerung in der Ebene als auch im Raum dar. Die pythagoreische Gleichung ist darüber hinaus auch in der Apollonios-Gleichung enthalten.
Ein räumliches Analogon ist der Satz von de Gua. Hier werden das rechtwinklige Dreieck durch ein rechtwinkliges Tetraeder und die Seitenlängen durch die Flächeninhalte der Seitenflächen ersetzt. Sowohl der Satz des Pythagoras als auch der Satz von de Gua sind Spezialfälle eines allgemeinen Satzes über n-Simplexe mit einer rechtwinkligen Ecke.
Unterschiede in der nichteuklidischen Geometrie
Nichteuklidische Geometrien sind Geometrien, in denen das Parallelenaxiom nicht gilt. Ein Beispiel hierfür ist die Geometrie der Kugeloberfläche. Dort gilt der Satz des Pythagoras nicht mehr, da in solchen Geometrien der Innenwinkelsatz nicht gilt, also die Winkelsumme eines Dreiecks von 180° verschieden ist. Ein anderes Beispiel ist der „gekrümmte“ Raum der Allgemeinen Relativitätstheorie Albert Einsteins.
Geschichte
Babylon und Indien
Bereits auf einer babylonischen Keilschrifttafel,[29] die in die Zeit der Hammurabi-Dynastie datiert wird (ca. 1829 bis ca. 1530 v. Chr.), findet sich eine geometrische Problemstellung mit Lösung, bei der der Satz zur Berechnung von Längen (im Sexagesimalsystem) verwendet wurde:[30][31]
Ein Balken, 0;30 (= 30/60 GAR = 1/2 GAR ≈ 3 m lang)[32]
Von oben ist er 0;6 (= 6/60 GAR) herabgekommen.
Von unten was hat er sich entfernt?
0;30 (= 30/60) quadriere, 0;15 (= 900/3600 = 15/60) siehst du.
0;6 (= 6/60) von 0;30 (= 30/60) abgezogen, 0;24 (= 24/60) siehst du.
0;24 (= 24/60) quadriere, 0;9,36 (= 576/3600) siehst du.
0;9,36 (= 576/3600) von 0;15 (= 900/3600) ziehe ab, 0;5,24 (= 324/3600) siehst du.
0;5,24 (= 324/3600) hat was als Quadratwurzel? 0;18 (= 18/60).
0;18 (= 18/60 GAR) am Boden hat er sich entfernt.
Daraus ergibt sich:
- , also und weiter .
Ein Interesse der Babylonier an einem mathematischen Beweis geht jedoch aus den Quellen nicht hervor.
Die Keilschrifttafel Plimpton 322 enthält außerdem verschiedene pythagoreische Tripel, unter anderem
- , sowie ,
was auf ein Verfahren zur Berechnung solcher Tripel schließen lässt.
In indischen Sulbasutras („Schurregeln“ bzw. „Leitfäden zur Meßkunst“), die ungefähr vom 6. bis zum 4. Jahrhundert v. Chr. entstanden, finden sich einige pythagoreische Tripel. Außerdem wurde auch der Lehrsatz dort schon allgemein ausgesprochen und benutzt.[33][34][35] Wie er begründet wurde, ist nicht sicher.[36]
China
Der Satz war im antiken China als Satz der Gougu (勾股定理) bekannt. In der Schrift Zhoubi suanjing („Arithmetischer Klassiker des Zhou-Gnomons“), die ungefähr vom 1. Jahrhundert v. Chr. bis zum 6. Jahrhundert n. Chr. entstand,[37] wird mit der sogenannten „Hypotenusen-Figur“ (Xian-tu)[38][39] ein dort am Beispiel des rechtwinkligen Dreiecks (gougu) mit den Seiten 3, 4 und 5 gegebener Beweis des Satzes veranschaulicht.[40] Auch im Jiu Zhang Suanshu („Neun Bücher arithmetischer Technik“, 1. Jahrhundert n. Chr.), dem klassischen mathematischen Werk Chinas mit einer Sammlung von 263 Problemstellungen, ihren Lösungen und den Lösungswegen, wird er angewendet. Liu Hui (3. Jahrhundert n. Chr.) gab wohl in seinem Kommentar zu den „Neun Büchern“ im neunten Kapitel einen Zerlegungsbeweis an.[41]
Die umstrittene Rolle des Pythagoras

Die Benennung des Satzes nach dem griechischen Philosophen Pythagoras (6. Jahrhundert v. Chr.) ist erst in späteren Quellen bezeugt. Daher ist in der Forschung die Frage nach der Rolle des Pythagoras stark umstritten. Verschiedene Hypothesen kommen in Betracht:
- Pythagoras übernahm den Satz von den Babyloniern, seine Rolle war nur die eines Vermittlers orientalischen Wissens an die Griechen. Antiken Quellen zufolge unternahm er eine Ägyptenreise, er soll sogar in Babylonien gewesen sein, doch ist die Glaubwürdigkeit der Berichte über seine Reisen umstritten.
- Pythagoras hat den Satz unabhängig von der orientalischen Mathematik entdeckt und auch erstmals bewiesen. Diese Ansicht war in der Antike verbreitet.
- Pythagoras verdankte die Kenntnis des Sachverhalts orientalischen Quellen, war aber der erste, der einen Beweis dafür fand. Tatsächlich waren Babylonier und Ägypter anscheinend nur an der Anwendung des Satzes für praktische Zwecke, nicht an einem allgemeingültigen Beweis interessiert. So enthält beispielsweise das älteste bekannte Rechenbuch der Welt, das ägyptische Rechenbuch des Ahmes (auch Papyrus Rhind) aus dem 17. Jahrhundert v. Chr., bereits komplizierte Aufgaben, es fehlt jedoch jede Verallgemeinerung, es wird nicht definiert und bewiesen.
- Pythagoras kannte einen der einfacheren Beweise, zum Beispiel einen Beweis vom Zerlegungstyp und für den Spezialfall eines Dreiecks mit einem rechten und zwei 45-Grad-Winkeln.[42]
- Pythagoras hat in der Geschichte des Satzes keine Rolle gespielt; erst spätere Pythagoreer haben möglicherweise den ersten Beweis gefunden.
Der historisch nachweisbare Zusammenhang von Pythagoras zu dem ihm zugeschriebenen Theorem ist nach Bartel Leendert van der Waerden[43] sehr zweifelhaft, und auch Thomas Heath sieht nur schwache historische Belege für die Zuschreibung.[44] Gegensätzliche Positionen vertreten zum Beispiel die Wissenschaftshistoriker Walter Burkert und Leonid Zhmud. Burkert zieht allenfalls eine Vermittlerrolle des Pythagoras in Betracht, Zhmud schreibt ihm mathematische Leistungen wie den Beweis des Satzes zu und betont seine Eigenständigkeit gegenüber der orientalischen Mathematik.[45][46][47]
Euklid, der in der zweiten Hälfte des 4. Jahrhunderts v. Chr. in seinem berühmten Werk Elemente das mathematische Wissen seiner Zeit zusammentrug, bot einen Beweis,[48] brachte den Satz aber nicht namentlich mit Pythagoras in Zusammenhang. Proklos schrieb dazu im 5. Jahrhundert n. Chr. in seinem Kommentar zu Euklids Elementen: „Wenn wir denen zuhören die sich gerne mit Geschichte befassen finden wir, dass sie dieses Theorem Pythagoras zuschreiben und sagen, er hätte dafür einen Ochsen geopfert“,[49][43] was zeigt, dass die Zuschreibung an Pythagoras damals verbreitet war. Auch Plutarch,[50] Cicero und Vitruv[51] berichten von Pythagoras Opferung eines Ochsen, mit unterschiedlichen Versionen zur Ursache – bei Vitruv ist es die Entdeckung eines rechtwinkligen Dreiecks mit den Seitenlängen 3, 4, 5, also einem pythagoreischen Tripel, Cicero (De natura deorum, Buch 3, 88) gibt keine genaueren Hinweise auf die zugrundeliegende geometrische Entdeckung.[44]
Der älteste Beleg dafür, dass der Satz mit Pythagoras in Verbindung gebracht wurde, ist ein Epigramm eines Apollodoros, der möglicherweise mit dem Philosophen Apollodoros von Kyzikos zu identifizieren ist; in diesem Fall stammen die Verse aus der zweiten Hälfte des 4. Jahrhunderts v. Chr. Der Text lautet:[52]
Als Pythagoras einst die berühmte Zeichnung gefunden,
Brachte als Opfer er dar herrliche Stiere dem Gott.
Apollodoros gibt nicht an, welche „berühmte“ Zeichnung oder Figur er meint, doch spätere Autoren, darunter Diogenes Laertios, der im 3. Jahrhundert die beiden Verse zitierte, gingen davon aus, dass es sich um den „Satz des Pythagoras“ handelt. Diese Überlieferung, wonach Pythagoras einem Gott zum Dank dafür, dass dieser ihm die Erkenntnis eingab, ein Rinderopfer darbrachte, steht – wie schon Cicero bemerkte – in Widerspruch zu dem von zahlreichen antiken Quellen überlieferten Umstand, dass Pythagoras und die Pythagoreer Tieropfer grundsätzlich ablehnten.[53][54]
Literarische Rezeption
Johannes Kepler schrieb in seinem Mysterium cosmographicum (Kapitel 13) von 1597: Die Geometrie hat zwei große Schätze: der eine ist der Satz des Pythagoras, der andere die Teilung der Linie in das extreme und mittlere Verhältnis[55] (dabei ist mit dem zweiten Schatz der Goldene Schnitt gemeint). Die Verbindung dieser beiden Sätze sind im Kepler-Dreieck ersichtlich.
Der Philosoph Thomas Hobbes begann, wie sein Biograph John Aubrey berichtete, mit 40 Jahren ernsthaft Mathematik zu studieren, nachdem er in einer Bibliothek ein Exemplar von Euklids Elementen auf der Seite des Beweises des Satzes von Pythagoras (Elemente, I, 47) aufgeschlagen fand, dies auf Anhieb nicht glauben wollte und sich von einer Proposition zur nächsten in den Elementen las, bis er von dessen Wahrheit überzeugt wurde. Anschließend fasste er eine Neigung zur Mathematik.[56]
Hans Christian Andersen verfasste 1831 einen Beweis des Satzes des Pythagoras in Gedichtform mit dem Titel Formens evige Magie (Et poetisk Spilfægterie).[57][58]
Adelbert von Chamisso schrieb 1836 in seinem Gedicht Vom Pythagoräischen Lehrsatz: Die Wahrheit, sie besteht in Ewigkeit / Wenn erst die blöde Welt ihr Licht erkannt / Der Lehrsatz, nach Pythagoras benannt / Gilt heute, wie er galt zu seiner Zeit.[59] Zu dem mythischen Opfer von hundert Ochsen, die Pythagoras angeblich als Dank für seine Entdeckung geopfert haben soll, fährt er in satirischer Weise fort: Die Ochsen seit dem Tage, wenn sie wittern / Daß eine neue Wahrheit sich enthülle / Erheben ein unendliches Gebrülle. Pythagoras erfüllt sie mit Entsetzen / Und machtlos, sich dem Licht zu widersetzen / Verschließen sie die Augen und erzittern.
Der Mathematiker und Schriftsteller Lewis Carroll schrieb ähnlich Chamisso 1890[60]: Aber weder 30 Jahre noch 30 Jahrhunderte beeinflussen die Klarheit oder den Charm geometrischer Wahrheiten. Ein Theorem wie „Das Quadrat der Hypotenuse eines rechtwinkligen Dreiecks ist gleich der Summe der Quadrate der Seiten“ ist heute von so blendender Schönheit wie an dem Tag, als Pythagoras es als Erster entdeckte.
Veranschaulichung

Sehr verbreitet sind Anschauungsobjekte, die mit Hilfe von Flüssigkeiten den Satz des Pythagoras beschreiben. Die nebenstehende animierte Prinzipskizze ist quasi die Vorderansicht eines drehbar gelagerten Exponates des Science-Center Phaeno in Wolfsburg.[61] An den Seiten des mittigen rechtwinkligen Dreiecks sind flache durchsichtige Behälter mit der Tiefe angebracht. Deren quadratische Grundflächen sind gleich den Flächen der Kathetenquadrate bzw. des Hypotenusenquadrates. Die Behälter sind deshalb mit , und bezeichnet. Ist das Exponat in seiner Ausgangsstellung ( unten), fließt das in und randvoll gefüllte blaue Wasser über die Ecken des Dreiecks und restlos ab und füllt somit vollständig . Daraus folgt
- ,
geteilt durch ergibt es
Verwandte Themen
- Pythagoreische Addition – die Wurzel aus der Summe der Quadrate mehrerer Werte
- Trigonometrischer Pythagoras – die Übertragung des Satzes auf die Winkelfunktionen Sinus und Cosinus
- Möndchen des Hippokrates
Literatur
- Anna M. Fraedrich: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994, ISBN 3-86025-669-6.
- Mario Gerwig: Der Satz des Pythagoras in 365 Beweisen. Springer Spektrum, Berlin 2021, ISBN 978-3-662-62886-7
- Dietmar Herrmann: Die antike Mathematik. Geschichte der Mathematik in Alt-Griechenland und im Hellenismus. Springer Spektrum, Berlin 2020, ISBN 978-3-662-61394-8 [darin: S. 41–67]
- Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977, ISBN 3-506-99189-2, S. 114–118.
- Alexander K. Dewdney: Reise in das Innere der Mathematik. Birkhäuser, Berlin 2000, ISBN 3-7643-6189-1, S. 47–76.
- Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0.
- Alfred S. Posamentier: The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books, Amherst 2010, ISBN 978-1-61614-181-3.
- Elisha Scott Loomis: The Pythagorean Proposition. Edwards Brothers, 2-te Auflage, Ann Arbor (MI) 1940 (Digitalisate: eric, archive.org)
Weblinks
- Vielzahl animierter Beweise des Satzes des Pythagoras, Landesbildungsserver Baden-Württemberg
- Beweise für den Satz des Pythagoras. ( vom 12. September 2010 im Internet Archive). Lehrstuhl für Didaktik der Mathematik, Universität Erlangen-Nürnberg
- Geometrische Beweise für den Satz des Pythagoras (Video)
- Sammlung von 122 Beweisen für den Satz des Pythagoras auf cut-the-knot (englisch)
- Interaktives Lernprogramm mit Beweisen, Aufgaben und vielen Links
- Eric W. Weisstein: Pythagorean theorem. In: MathWorld (englisch). (Enthält auch verschiedene Beweise)
- Eintrag Der Satz des Pythagoras im Lexikon der Mathematik (2017)
Einzelnachweise
- ↑ Ferdinand Rudio: Berliner philologische Wochenschrift. In: Internet Archiv. K.Fuhr, 16. Februar 1907, abgerufen am 9. Oktober 2021.
- ↑ a b Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik - 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen, Springer Spektrum, Springer-Verlag GmbH Berlin 2015, ISBN 978-3-662-45460-2, S. 46.
- ↑ Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0., S. XIII (Vorwort).
- ↑ Elisha S.Loomis: The Pythagorean Proposition, Cleveland 1927, 2. Auflage 1940, Nachdruck: The National Council of Teachers of Mathematics, Washington D. C. 1968.
- ↑ 371 nach Maor The Pythagorean Theorem, Princeton UP, S. 98. Loomis selbst gibt in der 2. Auflage 367 an. Die genaue Anzahl der Beweis in dem Buch von Loomis ist aufgrund seiner nicht durchgängigen Aufzählungsmethode und der Tatsache, dass einige zirkulär oder unzureichend sind und andere nur Variationen voneinander, nicht ganz klar, Hidden harmonies. The Live and Times of the Pythagorean Theorem, Bloomsbury Press, 2011, Kapitel 5.
- ↑ Gerwig, Der Satz des Pythagoras in 365 Beweisen, Springer Spektrum 2021.
- ↑ Euclids Elements, Book 1, Proposition 47, David Joyce.
- ↑ Euclids Elements, Book 6, Proposition 31, David Joyce.
- ↑ Eli Maor: The Pythagorean Theorem. Princeton University Press 2007, S. 42.
- ↑ Elemente, Buch 1, Proposition 48, David Joyce.
- ↑ John C. Sparks: The Pythagorean Theorem. Crown Jewel of Mathematics, AuthorHouse, Bloomington, Indiana 2008, S. 36.
- ↑ Maor, The Pythagorean Theorem, Princeton UP, 2007, S. 45.
- ↑ Schopenhauer, Die Welt als Wille und Vorstellung, Band 1, in Julius Frauenstädt (Hrsg.), Schopenhauers Sämtliche Werke, Band 2, Brockhaus, 2. Auflage 1877, S. 84.
- ↑ Felix Klein, Elementarmathematik vom höheren Standpunkt, Band 2, Springer 1925, S. 258.
- ↑ Zhou bi, Mathematischer Kanon des Zhou-Gnomons. Universität Bielefeld, abgerufen am 24. Mai 2019.
- ↑ a b C.J. Scriba, P. Schreiber: 5000 Jahre Geometrie — Zhoubi suanjing (Chou Pei Suan Ching). Hrsg.: H.-W. Alten, A. Djafari Naini, H. Wesemüller-Kock. 3. Auflage. Springer, Berlin, Heidelberg 2010, ISBN 978-3-642-02361-3, S. 111–113 (springer.com).
- ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie - Eine etwas andere Einführung in die Euklidische Geometrie. Zweite korrigierte und ergänzte Auflage, Springer Spektrum, Springer-Verlag GmbH, Berlin 2021, ISBN 978-3-662-63830-9, S. 29.
- ↑ Manon Bischoff: Der Satz des Pythagoras, Wale und Einsteins verschollener Beweis. In: Die fabelhafte Welt der Mathematik auf spektrum.de vom 18. August 2023. Siehe insbes. die beiliegende Zeichnung.
- ↑ Mario Gerwig, Der Satz des Pythagoras in 365 Beweisen, Springer Spektrum, S. 38, Beweis 15; doi:10.1007/978-3-662-62886-7. Dazu:
- Mario Gerwig: Rezension auf spektrum.de vom 10. November 2021.
- ↑ Michael de Villiers: Thabit’s Generalisation of the Theorem of Pythagoras. In: Learning and Teaching Mathematics. Nr. 23, 2017, S. 22–23.
- ↑ Aydin Sayili: Thâbit Ibn Qurra’s Generalization of the Pythagorean Theorem. In: Isis. Band 51, Nr. 1, 1960, S. 35–37 (JSTOR).
- ↑ George Gheverghese Joseph: The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press, 2011, ISBN 978-0-691-13526-7, S. 492.
- ↑ Howard Eves: Pappus’s Extension of the Pythagorean Theorem. In: The Mathematics Teacher. Band 51, Nr. 7 (November 1958), S. 544–546 (JSTOR:27955752).
- ↑ Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. M. A. A., Washington DC 2010, ISBN 978-0-88385-348-1, S. 77–78 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ a b Thomas Heath: A History of Greek Mathematics, Band 1,. (a) Hippocrates’s quadrature of lunes. In: wilbourhall. Clarendon Press, Oxford, 1921, S. 183 ff., Abbildung S. 185, abgerufen am 25. September 2019.
- ↑ Oskar Becker: Das mathematische Denken der Antike, Band 3. Mathematik des 5. Jahrhunderts. In: Google Books. Vandenhoeck & Ruprecht, Göttingen, 1966, S. 58, abgerufen am 26. September 2019.
- ↑ a b Euklid: Stoicheia. Buch VI. (PDF; 529 kB) In: opera-platonis.de/euklid. Abgerufen am 19. Mai 2019.
- ↑ Naber: Der Satz von Pythagoras ein Satz über Quadrate? Universität Bielefeld, abgerufen am 24. Mai 2019.
- ↑ London, British Museum, Keilschrifttafel 85196.
- ↑ Helmuth Gericke: Mathematik in Antike und Orient. Berlin 1984, S. 33 f.
- ↑ Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Hannover/Paderborn 1959, S. 67 f.
- ↑ Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Hannover/Paderborn 1959, S. 20.
Franz Lemmermeyer: Die Mathematik der Babylonier. (PDF; 7,6 MB) 2.4 Das Babylonische Maßsystem. Universität Heidelberg, 27. Oktober 2015, S. 44 ff., abgerufen am 23. Mai 2019. - ↑ Helmuth Gericke: Mathematik in Antike und Orient. Berlin u. a. 1984, S. 66–69.
- ↑ Oskar Becker: Das mathematische Denken der Antike. Göttingen 1966, S. 55 f. (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Ausführliche Darlegung des Sachverhalts bei Thomas L. Heath: The thirteen books of Euclid’s Elements. Band 1. 2. Auflage, New York 1956, S. 360–364.
- ↑ Oskar Becker: Die Grundlagen der Mathematik in geschichtlicher Entwicklung. Freiburg 1964, S. 20.
- ↑ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, S. 124, 126.
- ↑ Helmuth Gericke: Mathematik in Antike und Orient. Berlin 1984, S. 178 f.
- ↑ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, S. 298 f.
- ↑ Oskar Becker: Das mathematische Denken der Antike. Göttingen 1966, S. 56 (eingeschränkte Vorschau in der Google-Buchsuche).
Helmuth Gericke: Mathematik in Antike und Orient. Berlin 1984, S. 179 dagegen sieht darin noch keinen Beweis. - ↑ Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, S. 296–298. Die zugehörige Zeichnung, die für das richtige Verständnis benötigt wird, ist nicht erhalten geblieben.
- ↑ Maor, The Pythagorean Theorem, Princeton University Press 2007, S. 25.
- ↑ a b van der Waerden, Science Awakening, Kluwer 1988, S. 100.
- ↑ a b Heath, A History of Greek Mathematics, Oxford 1921, Band 1, S. 144.
- ↑ Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon. Nürnberg 1962, S. 405 f., 441 ff.
- ↑ Leonid Zhmud: Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Berlin 1997, S. 141–151, 160–163 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Siehe auch Thomas L. Heath: The thirteen books of Euclid’s Elements. Band 1. 2. Auflage. New York 1956, S. 350–360.
- ↑ Euklid: Elemente. Die Stoicheia. Buch 1, Satz 47. (PDF; 5,6 MB) In: opera-platonis.de. Abgerufen am 15. Juli 2019.
- ↑ Proclos, A commentary on the first Book of Euclid's Elements, Hrsg. Glenn R. Morrow, Princeton UP 1970, S. 337.
- ↑ Plutarch, Non posse suaviter vivi secundum Epicurum, Kapitel IX, Goodwin (Übersetzer), Cambridge UP 1874, Projekt Perseus.
- ↑ Vitruv, Ten Books on Architecture, Cambridge University Press 1999 (Hrsg. Ingrid D. Rowland), S. 107/108, Kapitel 9, Vorwort, Abschnitt 6.
- ↑ Apollodoros nach Diogenes Laertios 8,12, übersetzt von Otto Apelt: Diogenes Laertios: Leben und Meinungen berühmter Philosophen. 3. Auflage. Hamburg 1990, S. 116.
- ↑ Leonid Zhmud: Pythagoras and the Early Pythagoreans. Oxford 2012, S. 59, 257, 267–269.
- ↑ Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon. Nürnberg 1962, S. 168 und Anm. 152, S. 405 f.
- ↑ Aus dem Englischen übersetzt nach der Zitierung in Dan Pedoe Geometry and the liberal arts, St. Martin's Press 1976, S. 72. Der dort zitierte Folgesatz Den ersten können wir mit einem Batzen Gold vergleichen, den zweiten können wir als kostbares Juwel bezeichnen fehlt im lateinischen Original, Kepler, Mysterium Cosmographicum, Werkausgabe Band 8 (Franz Hammer Hrsg.), C. H. Beck 1963, S. 78 (Atque hactenus usui fuit aureum illud theorema Pythagorae potentijs laterum in triangulo rectangulo, prop. 47.lib. 1. In caeteris duobus corporibus altero illo Geometriae thesauro opus est de linea secundum extremam et mediam rationem secta, qui est propositio 30. sexti.). Dort ist einfach nur von zwei goldenen Sätzen der Geometrie die Rede, dem Satz des Pythagoras (Euklid, Elemente, I, 47) und dem Satz vom goldenen Schnitt (Euklid Elemente, VI, 30), wobei letzterer bei der Konstruktion des Dodekaeders verwendet wird, mit den anderen regulären Polyedern eines der Themen in Keplers Buch.
- ↑ Maor, The Pythagorean Theorem, 2007, S. 47.
- ↑ Hans Christian Andersen: H. C. Andersens samlede værker. Band 7: Digte I. 1823–1839. Kopenhagen 2005, S. 311–313, Kommentar S. 638–639 (visithcandersen.dk).
- ↑ Hans-Joachim Schlichting: Die Welt physikalisch gesehen. – Formen der ewigen Magie. In: hjschlichting.wordpress.com. 9. März 2017, abgerufen am 13. Juli 2020.
- ↑ Adelbert von Chamisso, Vom Pythagoräischen Lehrsatz, Bibliotheca Augustana.
- ↑ But neither thirty years, nor thirty centuries, affect the clearness, or the charm of Geometrical truths. Such a theorem as '"the square of the hypotenuse of a right -angled triangle is equal to the sum of the squares of the sides" is as dazzlingly beautiful now as it was in the day when Pythagoras first discovered it, …, in: Carroll, A new theory of parallels, Macmillan 1890, S. XVI, google books.
- ↑ Hans-Joachim Schlichting: Die Welt physikalisch gesehen. Der Satz des Pythagoras – revisited. In: hjschlichting.wordpress.com. 5. März 2017, abgerufen am 11. Juli 2019.




































































![{\displaystyle c^{2}=4\cdot {\frac {3\cdot 4}{2}}+\left(3-4\right)^{2}=3^{2}+4^{2}=25\;[\mathrm {FE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc3b4fe1fbe238c15b4cd02c4887e8943f1bb5c5)

![{\displaystyle c=5\;[\mathrm {LE} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dbfc76c882ce3c7564f3fffd877584e84d4fc90)




















































































