Anstiegs- und Abfallzeit
Unter Anstiegszeit und Abfallzeit (englisch rise time und fall time) versteht man in der Digitaltechnik und der Messtechnik die Zeit, die ein Pegelwechsel eines (idealerweise) rechteckförmigen Signals real benötigt, um seinen Signalpegel zwischen zwei definierten Zwischenwerten (üblich sind 10 % und 90 %) zu ändern.
Die Zeiten werden durch die endliche Grenzfrequenz der beteiligten Schaltelemente und Übertragungswege verursacht.
Digitaltechnik[Bearbeiten | Quelltext bearbeiten]
Anstiegs- und Abfallzeiten beschreiben in der Digitaltechnik und bei Schalttransistoren die beim Umschaltvorgang charakteristischen Zeiten, in denen das Signal nicht mehr den alten und noch nicht den neuen definierten Logikpegel („0“ bzw. „1“) bzw. Schaltzustand innehat. Siehe auch Flankensteilheit.
In der Digitaltechnik werden hierbei meistens die im ungünstigsten Fall (Worst Case) garantierten Zeiten genannt. Sie beschreiben die Zeit, die ein Signal (beispielsweise in einem Computerprozessor) zum sicheren Umschalten zwischen den beiden binären Zuständen benötigt. Die für ein Bauteil spezifizierten Anstiegs- und Abfallzeiten sind oft keine Messwerte, sondern bei bestimmten Parametern (Betriebsspannung, Temperatur) durch das Design und den Herstellungsprozess des Bausteins bzw. der betrachteten Logikfamilie gesicherte Mindestwerte.
Sämtliche Digitaltechnik basiert auf Schaltungselementen, die zwar für die Bearbeitung digitaler Signale optimiert sind, aber letztlich analog arbeiten. Dabei ist zu beachten, dass die Zuordnung von „1“ bzw. „0“ zu „Strom ein“ bzw. „Strom 0“ eine Idealisierung ist – in der Praxis wird hingegen normalerweise mit Spannungs- und Strompegeln gearbeitet, die von diesen Idealwerten abweichen. Weiterhin ist das Verhalten der Schaltung beim Zustandswechsel meistens unsymmetrisch, weshalb sich Anstiegs- und Abfallzeit dann mehr oder weniger stark unterscheiden.
Aufgrund der beschriebenen nichtidealen Eigenschaften ist es notwendig, Schwellenwerte für ein Logiksignal festzulegen. Für logisch „0“ wird bei TTL beispielsweise ein zulässiger Bereich von 0…0,8 V festgelegt und als logisch „1“ ein Bereich von 2…5 V. Die tatsächliche Schaltschwelle der Logikbausteine liegt im „verbotenen Bereich“ zwischen diesen beiden Werten (typisch bei ca. 1,4 V); sie wird daher während der Anstiegs- und Abfallzeit überschritten. Für die richtige Funktion von digitalen Schaltungen (Logikbausteinen) ist es notwendig, den verbotenen Bereich hinreichend schnell zu durchlaufen; entsprechend ist dann eine minimal zulässige Spannungsanstiegsgeschwindigkeit oder maximale Anstiegs-/Abfallzeit spezifiziert.
Anstiegs- und Abfall-Zeit beschreiben die Zeitintervalle, in denen dieser undefinierte „verbotene“ Zustand während des Umschaltens auftritt. Wichtig ist das insbesondere bei flankengetriggerten Schaltungen, d. h. Schaltungen, die auf die Änderung des Signals reagieren (z. B. flankengetriggertes Flipflop). Andernfalls kann es zu Fehlfunktionen kommen; siehe Race condition. Beispielsweise ist bei einem in HCMOS-Technik hergestellten Flipflop (SN74HC74) ein Wert von maximal 500 ns (Betrieb mit 4,5 V) spezifiziert.[1]
Um eine Sicherheit gegen Störungen zu erhalten, gelten für die Ausgänge dieser Bausteine härtere Anforderungen als für die Eingänge. Beispielsweise werden für einen Gatterausgang in der klassischen TTL-Technik max. 0,4 V für „0“ und min. 2,4 V für „1“ garantiert.
Sehr kurze Anstiegs- und Abfallzeiten im Signal bedeuten auch, dass im Spektrum des Signals sehr hohe Frequenzanteile vorhanden sind, die zur Aussendung (Abstrahlung) von elektromagnetischen Wellen führen. Durch diese Störsignale können andere Schaltungsteile in ihrer Funktion beeinflusst werden. Um die elektromagnetische Verträglichkeit sicherzustellen, werden deshalb die Ausgänge von Digital- und Treiberschaltungen so ausgelegt, dass die Anstiegs- und Abfallzeiten nur so kurz wie unbedingt nötig sind. Dazu wird die Flankensteilheit (slew rate) des Ausgangstreibers begrenzt.
Messtechnik[Bearbeiten | Quelltext bearbeiten]
In der Messtechnik sowie zur Charakterisierung analoger und digitaler Schaltungen werden zur Spezifizierung der Zeiten meistens die Werte von 10 % bzw. 90 % des Schaltpegels bzw. Sollsignales definiert.
Auch Schalttransistoren und andere leistungselektronische Bauteile werden damit charakterisiert.
Analoge Verstärker, Schaltverstärker, Leuchtdioden, Laser, Photodioden und Fototransistoren werden ebenfalls durch Anstiegs- und Abfallzeiten charakterisiert, die sie als Antwort auf eine Sprungfunktion liefern.
Wenn ein exponentieller Verlauf angenommen wird, beträgt die Anstiegs- und Abfallzeit für einen Tiefpass 1. Ordnung oder vergleichbare Systeme jeweils:
mit
- der Zeitkonstante
- der 3-dB-Grenzfrequenz .
Diese Formel wird meist an Filtern erster Ordnung hergeleitet. Bei Systemen höherer Ordnung ist der Fehler recht gering, d. h. z. B. auch bei Tiefpaßfiltern höherer Ordnung kann man die Anstiegszeit relativ genau aus der 3-dB-Grenzfrequenz berechnen; das meist auftretende Überschwingen hat darauf relativ wenig Einfluss.
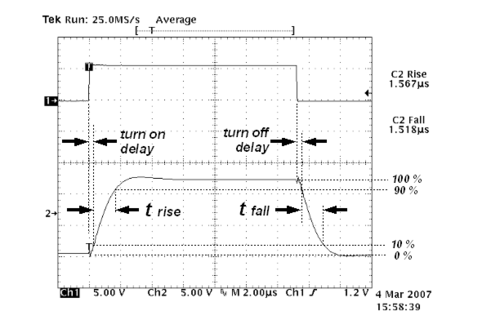
Sowohl bei Digitalschaltungen als auch bei Verstärkern, Sensoren und Aktoren sind zusätzliche Verzögerungszeiten charakteristisch (englisch delay times, bei Schaltstufen turn-on delay und turn-off delay). Diese vergehen, bis sich nach einem Sprung des Eingangssignals die Ausgangsspannung zu ändern beginnt, d. h. bevor die eigentliche Anstiegs- bzw. Abfallszeit anfängt, und hängen von weiteren Polen und Nullstellen der Übertragungsfunktion oder auch von nichtlinearen Speichereffekten ab.
Die gesamte Zeitverzögerung beim Durchlauf eines Signals durch eine Schaltstufe oder einen anderen Vierpol ergibt sich somit aus der Verzögerungs- und ungefähr der halben Anstiegs- bzw. Abfallzeit.
Viele digitale Speicheroszilloskope verfügen über Messfunktionen für die Verzögerungs- sowie für die Anstiegs- und Abfallzeiten.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Datenblatt von Texas Instruments: SNx4HC74 Dual D-Type Positive-Edge-Triggered Flip-Flops With Clear and Preset, „SCLS094E“, Dezember 1982, überarbeitet im Dezember 2015


