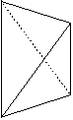
Disphenoid

Ein Disphenoid (auch gleichschenkliges Tetraeder[1]) ist ein Polyeder mit vier kongruenten Dreiecken als Seitenflächen. Ein Disphenoid besteht aus zwei Sphenoiden (zu altgriechisch σφήν „Keil“), das sind offene Formen mit je zwei Flächen (Dieder).
Der Begriff „gleichschenkliges Tetraeder“ bedarf einer Erklärung: Ein Disphenoid ist ein Tetraeder im allgemeinen Wortsinn, nicht notwendigerweise ein Tetraeder im Sinne des gleichnamigen platonischen Körpers. Das Adjektiv „gleichschenklig“ bezieht sich nicht auf seine Dreiecksflächen, sondern auf die Eigenschaft des Körpers, dass von seinen sechs Kanten die jeweils einander gegenüberliegenden die gleiche Länge haben.
Charakterisierungssätze[Bearbeiten | Quelltext bearbeiten]
Nach dem Satz von Bang[2] ist ein Disphenoid ein dreidimensionales Simplex mit einer der folgenden äquivalenten Charakterisierungen:
- Die jeweils gegenüberliegenden (unverbundenen) Kanten haben die gleiche Länge.
- Die 4 Dreiecke sind kongruent.
- Die 4 Dreiecke haben denselben Umfang.
- Die 4 Dreiecke haben dieselbe Fläche.
Ein anderer Charakterisierungssatz ist der folgende:
- Ein Tetraeder ist genau dann ein Disphenoid, wenn die Inkugel und die Umkugel konzentrisch sind.[3]
In voller Allgemeinheit gilt sogar folgender Charakterisierungssatz:
- Ein Tetraeder ist genau dann gleichschenklig, wenn von den vier Punkten:
- – Mittelpunkt der Inkugel
- – Mittelpunkt der Umkugel
- – Monge-Punkt
- – Schwerpunkt
- mindestens zwei zusammenfallen. In diesem Falle fallen sogar alle vier Punkte zusammen.[3]
Bemerkung:
Die Dreiecke haben alle dieselbe Orientierung.
Spezialfälle[Bearbeiten | Quelltext bearbeiten]
Ist eines der Dreiecke (und damit alle) gleichschenklig, so spricht man von einem tetragonalen Disphenoid. Dann sind 4 Kanten des Disphenoids gleich lang und die übrigen 2 stehen windschief senkrecht aufeinander.
Sind die Dreieckseiten verschieden, so wird das Disphenoid rhombisch genannt.
(Diese Begriffsbildungen stammen aus der Kristallographie.)
Ist ein Dreieck (und damit alle) gleichseitig, dann ist das Disphenoid ein regelmäßiges Tetraeder.
Berechnung eines beliebigen Disphenoids[Bearbeiten | Quelltext bearbeiten]
Ein Disphenoid ist durch eines der 4 kongruenten Dreiecke bestimmt. Da ein Dreieck durch 3 voneinander unabhängige Angaben zur Größe seiner Seiten und/oder Winkel bestimmt ist, ist ein Disphenoid ebenfalls durch 3 voneinander unabhängige Angaben bestimmt.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Disphenoide kommen in der Natur als Kristallform vor: Sie sind die allgemeine Flächenform der Kristallklassen 222 (rhombisch-disphenoidische) und 4 (tetragonal-disphenoidische Klasse).
-
Dieder (Sphenoid)
-
rhombisches Disphenoid mit drei ungleichen Achsen A, B, C
-
tetragonales Disphenoid
-
Spezialfall: reguläres Tetraeder mit sechs gleichen Kanten
Weblinks[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Nathan Altshiller-Court: Modern Pure Solid Geometry. 2. Auflage. Chelsea Publishing Company, Bronx, NY 1964, ISBN 0-8284-0147-0.
- Adolf Schmidt, Das gleichseitige Tetraeder, Zeitschrift für Mathematik und Physik XXIX, S. 321–343. Teubner, Leipzig (1884).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Eric W. Weisstein: Isosceles Tetrahedron. In: MathWorld (englisch).
- ↑ Ross Honsberger: Mathematische Juwelen. Verlag Vieweg, 1982, ISBN 3-528-08475-8, S. 82.
- ↑ a b N. Altshiller-Court: Modern Pure Solid Geometry. 1964, S. 105–108.