Dynamisches System (Systemtheorie)
Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Das System kann beispielsweise ein mechanisches Gebilde, ein elektrisches Netzwerk, aber auch ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein.
Das System hat mindestens einen Signaleingang und einen Signalausgang und reagiert zu einem bestimmten Zeitpunkt auf ein beliebiges Eingangssignal mit einer bestimmten zeitlichen Reaktion auf das Ausgangssignal. Die in dem System enthaltenen Energiespeicher als Ursache des Zeitverhaltens können je nach Beobachtungszeitpunkt gewollt oder ungewollt einen Systemzustand ≠ 0 im Zustandsraum einnehmen, bei dem sich die Wirkung des Eingangssignals mit dem Systemverhalten und dem Systemzustand auf das Systemausgangssignal überlagert.
Elementare Begriffe des dynamischen Systems[Bearbeiten | Quelltext bearbeiten]
Ein technisches dynamisches System enthält einen oder mehrere Energiespeicher, die konzentriert oder räumlich verteilt angeordnet sind. Häufig werden bei Systemberechnungen zur Vereinfachung konzentrierte Energiespeicher angenommen. Dynamische Systeme mit konzentrierten Systemspeichern enthalten Variablen als Funktion der Zeit. Dynamische Systeme mit räumlicher Verteilung der Systemspeicher enthalten Variablen als Funktionen der Zeit und des Ortes.
Ein dynamisches System ist eine Funktionseinheit zur Verarbeitung und Übertragung von Signalen, wobei die Systemeingangsgröße als Ursache und die Systemausgangsgröße als zeitliche Auswirkung definiert ist.
Ferner können die internen Energiespeicher Anfangswerte enthalten, wenn das Signalverhalten eines Systems zu einem bestimmten Zeitpunkt innerhalb eines Einschwingvorgangs für betrachtet werden soll.
- Das Ausgangs-Eingangsverhalten dieser Systeme kann linear, kontinuierlich nichtlinear, diskontinuierlich nichtlinear, zeitinvariant, zeitvariant und totzeitbehaftet sein. Dies gilt für Eingrößen- und Mehrgrößensysteme.
- Definition Linearität: Ein System verhält sich linear, wenn es das Superpositionsprinzip (Überlagerungsprinzip) und das Verstärkungsprinzip erfüllt.[1]
- Eine grafische Darstellung des Ausgangs-Eingangsverhaltens des linearen dynamischen Systems mit asymptotisch stabilem Verhalten muss nach genügend langer Zeit immer eine unbegrenzte Gerade zeigen, die vom Ursprung versetzt sein kann.[2]

- Definition nichtlineares System: Statische kontinuierlich nichtlineare Systeme ändern ihre Verstärkung nach einer bestimmten Funktion. Nichtlineare dynamische Systeme bereiten in der Systemberechnung Probleme, weil sie selten analytisch lösbar sind. Übliche Systembeschreibungen erfolgen durch die numerische zeitdiskrete Berechnung mit logischen Befehlen und Differenzengleichungen. Nichtlineare dynamische Systeme können zur einfacheren Berechnung auch durch Modelle in Kombinationen von nichtlinearen Systemen ohne Zeitverhalten und linearen dynamischen Systemen aufgeteilt werden, z. B. nach dem Hammerstein-Modell. Nichtlineare statische Modelle sind meist Unikate.[3]
- Komplexe dynamische Systeme bestehen allgemein aus mehreren Teilsystemen bestimmter Struktur, die in Signalflussplänen (Blockschaltbildern) als Reihen-, Parallel- und Rückführschaltungen dargestellt werden.
- Statische lineare oder nichtlineare Systeme haben keine Energiespeicher und damit kein Zeitverhalten. Das Ausgangs-Eingangsverhalten wird durch algebraische oder transzendente Funktionen oder Wertetabellen beschrieben.
- → Siehe Wikibooks: Einführung in die Systemtheorie/ Beschreibung linearer Prozesse im Zeitbereich:
- Wikibooks: Linearitätseigenschaften – Lern- und Lehrmaterialien
Mathematische Verfahren zur Systembeschreibung und Systemberechnung[Bearbeiten | Quelltext bearbeiten]
Mathematische Modelle der dynamischen Systeme werden je nach Kenntnis und Verfügbarkeit der Systemparameter durch verschiedene mathematische Beschreibungsmethoden gekennzeichnet bzw. angenähert.
Die bekannteste Systembeschreibung ist die Differenzialgleichung. Andere bekannte Systembeschreibungen der dynamischen Systeme lassen sich von den Differenzialgleichungen entwickeln, wie die Übertragungsfunktion mit dem komplexen Frequenzbereich F(s), der Frequenzgang F(jω), die Zustandsraumdarstellung f(t), die für die numerische Berechnung benötigten Differenzengleichungen f(k,Δt), sowie die zugehörige z-Übertragungsfunktion.
Die Berechnung dynamischer Systeme dient der Kenntnis des Ausgangs-Eingangsverhaltens und der Systemanalyse. Je nach Art des dynamischen Systems eignen sich verschiedene mathematische Beschreibungs- und Berechnungsverfahren.
Dynamische Systeme mit Totzeitverhalten (Transportzeit) können praktisch nur mit numerischen zeitdiskreten Verfahren berechnet werden.
Übersicht Differenzialgleichungen[Bearbeiten | Quelltext bearbeiten]
- ; Gewöhnliche Differenzialgleichung höherer Ordnung mit konstanten Koeffizienten
- Eine gewöhnliche Differenzialgleichung ist eine Gleichung, die eine oder mehrere Ableitungen einer unbekannten Funktion enthält. Die Bezeichnung „gewöhnlich“ bezieht sich darauf, dass die gesuchte Funktion nur von einer Variablen abhängt. Eine lineare gewöhnliche Differenzialgleichung enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen, anderenfalls wird die Differenzialgleichung nichtlinear. Nichtlineare Differenzialgleichungen mit den verschiedenen Arten der Nichtlinearität sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. Solche dynamischen Systeme können mittels der numerischen zeitdiskreten Methoden beschrieben und berechnet werden.
- Die häufigsten mathematischen Systembeschreibungen linearer Systeme sind gewöhnliche Differenzialgleichungen mit konstanten Koeffizienten. Zur Aufstellung der Differenzialgleichungen höherer Ordnung werden Bilanzgleichungen der Energie / Materie-Speicher benötigt. Systeme mit konzentrierten Speichern erfordern für jede Speicherfunktion eine Differenzialgleichung 1. Ordnung.[4]
- Bei dynamischen Systemen in Form ausgeführter technischer Anlagen stehen Differentialgleichungen selten zur Verfügung. Das Systemverhalten muss erst noch analysiert und dann formuliert werden.
- Beispiel einer gewöhnlichen Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten a und b für ein System mit dem Ausgangssignal y(t) und Eingangssignal u(t):
- Konventionelle Lösung der gewöhnlichen Differenzialgleichung:
- Die Lösung einer Differenzialgleichung (DGL) erfolgt immer durch Integration und ist eine Funktion, nicht ein Wert.
- Mit dem Lösungsansatz (λ = Nullstelle) ergibt sich ein universelles Lösungsverfahren für die homogene Lösung der DGL beliebiger Ordnung mit konstanten Koeffizienten (siehe Charakteristische Gleichung).
- Gesamtlösung besteht aus zwei Lösungsanteilen: y(t) = Homogene Lösung yH(t) + Partikuläre Lösung yP(t)
- Homogene Lösung:
- Bedingung: Die homogene Lösung bezieht sich nur auf Anfangswerte. Die System-Eingangserregung ist Null. Nachteil: Umständliche Berechnung der Integrationskonstanten C.
- Partikuläre Lösung für der DGL über das Faltungsintegral oder über die Laplace-Transformation.
- Bedingung: Alle Anfangswerte sind gleich Null. Die Eingangserregung ist von Null verschieden. Das Faltungsintegral für Systeme höherer Ordnung ist schwierig zu lösen.
- Lösung des zeitlichen Systemverhaltens aus der Übertragungsfunktion der DGL bei einem gegebenen Eingangssignal U(s):
- Bei der gewöhnlichen DGL höherer Ordnung eignet sich besser der Lösungsweg über die Laplace-Transformation oder über die numerische Berechnung mit der diskreten Zeit. Bei der Anwendung zur Lösung einer DGL über die Übertragungsfunktion mit Hilfe der inversen Laplace-Transformation wird die analytische Lösung im Zeitbereich über den Suchbegriff in der Laplace-Transformationstabelle in Operatorenschreibweise gefunden.
- ; Differenzialgleichung höherer Ordnung mit variablen Koeffizienten
- Sind diese Koeffizienten oder nur ein Koeffizient dieser Differenzialgleichung variabel, dann ändert sich das Zeitverhalten des dynamischen Systems, d. h. eine Sprungantwort des Systems für einen gegebenen Eingangssprung nimmt einen anderen zeitlichen Verlauf. Dieses Verhalten wird leicht verständlich, wenn man die Laplace-transformierte Differenzialgleichung als Übertragungsfunktion betrachtet.
- Sind die Koeffizienten zeitabhängig, führt dieses zu zeitvariantem Systemverhalten, d. h. das Zeitverhalten des Systems ist zu unterschiedlichen Zeitpunkten für t > t0 unterschiedlich. Systembeispiel: Wenn bei einer beschleunigten Rakete die Masse des Treibstoffs sich ändert.
- ; Partielle Differenzialgleichung
- Bei partiellen Differenzialgleichungen hängt die gesuchte Funktion von mehreren Variablen ab. Es wird nach mehreren Variablen abgeleitet. Die Anwendung dieser Gleichung erfolgt z. B. bei dynamischen Systemen mit Zeit- und Ortskoordinaten.
- Systembeispiel: Signalübertragung bei langen elektrischen Leitungen oder Wärmefluss in homogenen Medien (Flüssigkeiten, Metalle, Stein).
Grundlagen Laplace-Übertragungsfunktion[Bearbeiten | Quelltext bearbeiten]
Die Übertragungsfunktion mit der komplexen Frequenz s entsteht aus der Laplace-Transformation einer linearen Differenzialgleichung mit konstanten Koeffizienten. Die Zerlegung der entstehenden Polynomgleichung erfolgt durch die Pol-Nullstellenbestimmung (sp und sn) in Linearfaktoren. Die Darstellungsformen der Übertragungsfunktion als rational gebrochene Funktion unterscheiden die faktorisierte Pol-Nullstellendarstellung und die Zeitkonstantendarstellung.[5]
Weitere Entstehungsweisen sind über System-Identifikationsmethoden mittels Testsignalen, durch Messen des Frequenzgangs des Systems oder über Spannungsteiler aus einem rückwirkungsfreien Impedanzverhältnis möglich.
Die Übertragungsfunktion ist die häufigste Systemdarstellung, weil nur 3 Formen – je im Zähler und Nenner – von Linearfaktoren oder deren Vielfache von differenzierenden und verzögernden linearen elementaren Grundsystemen existieren und die Wiedererkennung des Systems anhand der Gleichung hoch ist.
Alle Terme im Zähler und Nenner der Übertragungsfunktion können algebraisch behandelt werden. Im Zeitbereich bestimmen Linearfaktoren im Nenner das Systemzeitverhalten und wirken integrierend oder zeitverzögernd. Linearfaktoren im Zähler bestimmen die Größe der Amplituden und haben ein differenzierendes Verhalten.
Die Übertragungsfunktion in Polynom-Darstellung und Zeitkonstanten-Darstellung mit T = 1/sp und Tv = 1/sn lautet:
Begriffsklärung Zustandsraumdarstellung[Bearbeiten | Quelltext bearbeiten]
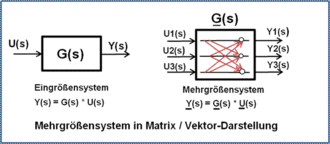
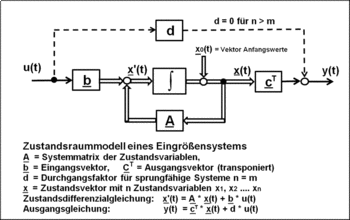
Unter dem Begriff Zustandsraumdarstellung versteht man die Beschreibung eines dynamischen Übertragungssystems durch seine Zustandsgrößen (= Zustandsvariablen). Dabei wird die systembeschreibende Differenzialgleichung n-ter Ordnung mit n konzentrierten Energiespeichern in n Differenzialgleichungen 1. Ordnung zerlegt und in eine Matrizen/Vektor-Darstellung gebracht. Die Zustandsvariablen beschreiben physikalisch den Energiegehalt der in einem technischen dynamischen System enthaltenen Speicherelemente.[6]
Lineare und nichtlineare dynamische Systeme, auch Mehrgrößensysteme können so behandelt werden. Lineare dynamische Systeme mit Anfangswerten können relativ einfach mit der Regelungsnormalform des Zustandsraumes numerisch berechnet werden, ohne Überführung in die Matrizen/Vektor-Darstellung.
Grundlagen „Numerische Berechnung dynamischer Systeme“[Bearbeiten | Quelltext bearbeiten]
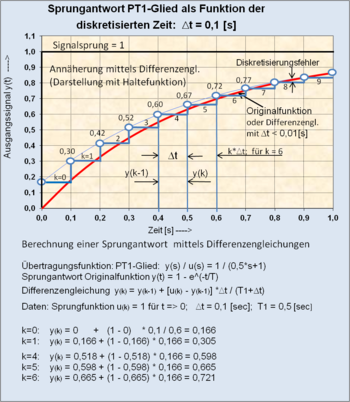
Für die Berechnung linearer und nichtlinearer totzeitbehafteter Systeme kommt praktisch nur die numerische Berechnung mit der diskreten Zeit Δt infrage. Sie entspricht in der einfachsten Form der menschlichen Denkweise für ein lineares System in Operatorendarstellung des Ausgangssignals für ein gegebenes Eingangssignal .[7]
Je nach der Systemeigenschaft wird schrittweise für eine kleine Zeitdifferenz ein neues Ausgangssignal berechnet. Für jede neue Berechnungsfolge eines Teilsystems bezieht sich das aktuelle Ausgangssignal additiv auf eine zurückliegende Folge .
Numerische Lösungen der Berechnung des Systemverhaltens sind üblicherweise tabellarisch in ki Zeilen dargestellt. Jede Zeile enthält die gleichen logischen Befehle (bei Nichtlinearität) und Differenzengleichungen.
Differenzengleichung[Bearbeiten | Quelltext bearbeiten]
Differenzengleichungen beschreiben im einfachsten Falle Differenzialgleichungen 1. Ordnung, deren Differentialquotienten durch Differenzenquotienten ausgetauscht wurden. Sämtliche linearen Systeme höherer Ordnung können mit Hilfe von 4 Arten von Differenzengleichungen beschrieben werden, auch schwingende Systeme mit konjugiert komplexen Polpaaren.
Beispiel einer Differenzengleichung der Integrationsfunktion nach dem Rückwärts-Differenzenquotient-Verfahren.
Abgetastete lineare dynamische Systeme im Online-Betrieb wie auch Simulationen von dynamischen Systemen werden mit Differenzengleichungen berechnet.
- → Ausführliche Details, siehe Artikel Differenzengleichung (Differenzenverfahren).
- → Siehe auch Artikel Seminumerischer Algorithmus für gemischte verschiedenartige Übertragungssysteme.
Berechnungsbeispiele linearer Systeme[Bearbeiten | Quelltext bearbeiten]
Fremderregter Gleichstrom-Nebenschlussmotor mit asymptotischem Verhalten[Bearbeiten | Quelltext bearbeiten]
- Es handelt sich um ein lineares asymptotisch stabiles System mit einem Systemeingang u(t) als Ankerspannung und einem Systemausgang y(t) als Drehzahl. Dieses System wird durch eine gewöhnliche Differenzialgleichung 2. Ordnung beschrieben (Zeitverzögerungen: Induktivität der Magnetspulen, Magnetkraft zur Beschleunigung der Ankermasse).
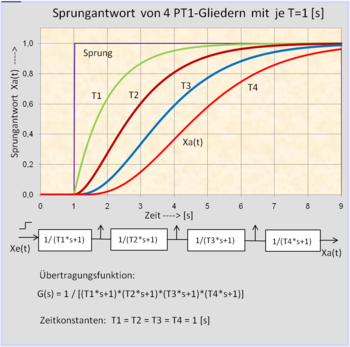
- Die Ruhelage des Systems ist nach genügend langer Zeit proportional abhängig von der Größe des Eingangssignals.
- Es handelt sich um ein Verzögerungssystem 2. Ordnung, das im komplexen Frequenzbereich 2 reelle Pole aufweist.
- Systembeschreibende gewöhnliche Differenzialgleichung mit den Koeffizienten an und bm:
- Bei Anwendung der Laplace-Transformation der Differenzialgleichung entsteht die Polynomdarstellung der Übertragungsfunktion G(s). Mit Hilfe der Pol-Nullstellenzerlegung ergibt sich die Produktdarstellung der Übertragungsfunktion.
- Übertragungsfunktion in Zeitkonstantendarstellung:
- Lösung der Funktion der Systemausgangsgröße mit Hilfe der Laplace-Transformationstabellen für einen normierten Eingangssprung 1(t):
Numerische Berechnung eines Übertragungssystems 2. Ordnung mit Hilfe der Regelungsnormalform der Zustandsraumdarstellung[Bearbeiten | Quelltext bearbeiten]
Die bis in die 1960er Jahre bevorzugte Lösung einer systembeschreibenden Differenzialgleichung durch einen Analogrechner ähnelt sehr stark der Regelungsnormalform des Zustandsraumes.
Die Ausgangswerte der Integratoren können zu einem beliebig wählbaren Zeitpunkt für den Wert Null haben, oder auf einen beliebigen Anfangswert gesetzt werden, unabhängig davon, ob die Eingangsgröße einen Wert ungleich Null oder gleich Null hat. Die Ausgänge der Integratoren sind die Zustandsvariablen und jeweils die Lösungen der Differentiale, indem sie mit den zugehörigen Koeffizienten auf den Eingang der höchsten Ableitung zurückgeführt werden. Die gesuchte Funktion der Ausgangsgröße entspricht der Zustandsvariablen .
Die Berechnung des Signalflussplans wird numerisch durchgeführt und bezieht sich auf die explizite Form der Differenzialgleichung, bei der die höchste Ableitung der Ausgangsgröße von der Gleichung freigestellt wird.[8][9]
Beispiel der GDGL eines Feder-Masse-Dämpfungssystems mit dem Eingangssignal
Im universitären Fachbereich technischer Studienrichtungen wird das Federpendel als ein Übertragungssystem zweiter Ordnung in vielen Fällen als System mit einem Eingang und einem Ausgang definiert. Das linear gedämpft schwingende System verfügt meist über einen Systemeingang und einen Systemausgang als Position (Lage) der Masse. Folgende Anwendungsfälle treten auf:
- Anwendungsfall
- Auf den Körper der Masse wirken die äußere Kraft sowie die Dämpfungs- und die Federkraft. Die Federkraft in der Ruhelage wird zu Null gesetzt.
- Nach genügend langer Zeit ist die Ruhelage der Masse abhängig von der Eingangsgröße , von der Federkonstante und der Masse .
- Anwendungsfall
- Das System mit ist in Bewegung, wenn zum Zeitpunkt Anfangswerte und deren Ableitungen der inneren Energiespeicher gegeben sind.
- Nach genügend langer Zeit ist die Ruhelage der Masse durch die Größe der Masse und durch die Federkraft bestimmt.
Es handelt sich bei dem Federpendel um ein lineares Verzögerungssystem 2. Ordnung, das im komplexen Frequenzbereich ein konjugiert komplexes Polpaar aufweist. Das System schwingt gedämpft, wenn die Dämpfungskonstante ist. Bei tritt der aperiodische Grenzfall des Systems ein. Die zugehörige Übertragungsfunktion G(s) lasst sich in 2 PT1-Glieder zerlegen.
Differenzialgleichung der Schwingbewegung mit Signaleingang und Signalausgang : (m = Masse, d = Dämpfungskonstante, k = Federkonstante, b0 = Faktor)
Signalflussplan für die homogene und partikuläre Lösung der GDGL zweiter Ordnung[Bearbeiten | Quelltext bearbeiten]

In dem dargestellten Signalflussplan sind alle Koeffizienten der GDGL durch den Koeffizienten der höchsten Ableitung dividiert worden, um freistellen zu können. Der Signalflussplan entspricht der expliziten Darstellung der GDGL, also der Form der freigestellten Gleichung nach der höchsten Ableitung .
Der Signalflussplan wird wie dargestellt numerisch berechnet, indem jede mathematische Operation der Koeffizienten und Differenzengleichungen hintereinander erfolgt. Da das Ergebnis der numerischen Berechnung immer tabellarisch erfolgt, gehören sämtliche Berechnungen entsprechend der Folge innerhalb einer Zeile. Jede Gleichung besetzt eine Spalte der gleichen Zeile. Es werden identische Zeilen hintereinander berechnet.
Die allgemeine Form der Schwingungsgleichung lautet:
Zur Durchführung der Berechnung wird die GDGL nach der höchsten Ableitung umgestellt und freigestellt.
Der dargestellte Signalflussplan erzwingt die Lösung der GDGL zweiter Ordnung für . Es hängt nun davon ab, ob eine:
- homogene Lösung mit Anfangswerten und ,
- partikuläre Lösung mit ohne Anfangswerte,
- eine Gesamtlösung mit Anfangswerten und gewünscht wird.
Zur Berechnung der Komponenten des Signalflussplanes sind folgende numerische Operationen erforderlich:
Algebraische Operationen wie z. B. die Differenz der Koeffizienten von der Eingangsgröße sind entsprechend der Folge bzw. der Folgegleichungen nummeriert.
- .
Für die homogene Lösung ist die Eingangsgröße .
Für die Berechnung der Integratoren gilt die Differenzengleichung der Integration (Euler-Rückwärts):
Der Term bedeutet hier allgemein die Eingangsgröße für jede Folge der Differenzengleichung. Dies ist in den meisten fällen nicht die System-Eingangsgröße , sondern es handelt sich um den in der tabellarische Darstellung stehenden Eingangswert, der in der gleichen Zeile links neben der Spalte der Differenzengleichung liegt. Je nach Aufgabenstellung ändert sich ständig mit steigender Folge. Bei mehreren Differenzengleichungen in Reihenschaltung ist die Ausgangsgröße die Eingangsgröße der nächsten Differenzengleichung .
Die Integrationskonstante hat ohne besondere Spezifikation den Wert 1.
bezieht sich auf das Ergebnis einer um zurückliegenden Folge (Zeile) der gleichen Spalte der Differenzengleichung.
Da zwei Integratoren in Reihenschaltung vorliegen, ist die Ausgangsgröße des ersten Integrators die Eingangsgröße des zweiten Integrators. Die Ausgangsgröße des zweiten Integrators ist die gesuchte Funktion der gleichen Folge für einen Stützpunkt in Annäherung an die analytische Funktion.
Liegen Anfangswerte der GDGL vor, werden für den entsprechenden Integrator für die Berechnungsfolge anstelle des Wertes (1. Zeile der Tabelle) die Anfangswerte der zwei Differenzengleichungen eingegeben.
Da die numerische Lösung der GDGL eine Annäherung an die Originalfunktion darstellt, hängt die Genauigkeit der Berechnung für die angegebene Differenzengleichung von der Größe der diskreten Zeit ab. Wird für ein Wert von ca. 0,1 % von der dominanten System-Zeitkonstante gewählt, ist ein Annäherungsfehler von ca. 0,1 % zu erwarten.
Beispiel der homogenen Lösung eines senkrecht schwingenden Federpendels ohne Eingangssignal u(t) = 0 mit Anfangswerten[Bearbeiten | Quelltext bearbeiten]

Siehe Bild: Signalflussplan der Regelungsnormalform für ein Übertragungssystem 2. Ordnung!
Das Federpendel kann auch als ein System mit einem Eingangssignal = Null zum Zeitpunkt mit den Anfangswerten der Federkraft und der Masse definiert werden. In diesem Fall ist das System zum Zeitpunkt sich selbst überlassen und strebt eine Ruhelage an, die durch die Federkraft, Masse und Dämpfung bestimmt wird.
Die Anfangswerte werden wie folgt definiert:
- Die Lage der Masse im Ruhezustand wird als Null festgelegt.
- Die Lage der Masse wird auf eine Höhe mit dem Anfangswert angehoben definiert und zum Zeitpunkt fallen gelassen.
- Der Anfangswert des ersten Integrators muss im angehobenen Zustand der Masse den Wert Null, also annehmen, anderenfalls kann der Anfangswert nicht auf den Anfangswert verharren. Ein konstanter Ausgangswert bei zwei hintereinander geschalteten Integratoren ist nur möglich, wenn der Ausgangswert des ersten Integrators gleich Null ist.
Für die homogene Lösung der GDGL des Federpendels sind folgende rekursive Berechnungen nach dem Signalflussplan erforderlich:
- Die Eingangsgröße ist gleich Null.
- . Diese mit den Koeffizienten bewertete Ausgangsgrößen der Integratoren wirken als Eingangsgröße auf .
- Differenzengleichung des ersten I-Gliedes:
- . Der Ausgangswert des ersten Integrators ist der Eingangswert des zweiten Integrators. ()
- Differenzengleichung des zweiten I-Gliedes:
- . Der Ausgangswert des zweiten Integrators ist das Ergebnis einer Berechnungszeile. ()
- Die erste Berechnungszeile für enthält die Anfangswerte der Integratoren und der Differenzengleichungen. Alle übrigen Gleichungen in dieser Zeile haben den Wert Null.
Werden diese Gleichungen für eine grafische Darstellung mit einer Betrachtungszeit von 10 Sekunden mit berechnet, sind 1000 identische Berechnungsfolgen (Zeilen) erforderlich. Jede Folge liefert im Abstand für einen Wert. Der größte Approximationsfehler beträgt wegen der gewählten Größe von etwa 1 %.
Mit Ausnahme der Folgegleichung für (1. Zeile) sind alle weiteren Folgegleichungen (Zeilen) identisch.
Tabellarische Berechnung des Pendels:
Zur Berechnung der Koeffizienten als Eingangsgröße des ersten Integrators der Folge stehen die Werte von und noch nicht zur Verfügung. Deshalb müssen diese Werte von einer zurückliegenden Folge entnommen werden. Zur Vermeidung von Rundungsfehlern, die sich addieren, wurde mit sehr hoher Stellenzahl der Tabellenkalkulation gerechnet.
| Folge k | Diskrete Zeit |
Koeffizienten |
Erste numerische Integration |
Zweite numerische Integration |
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| 1 | 0,01 | −6,250 | −0,0625 | 0,999375 |
| 2 | 0,02 | −6,199219 | −0,1244922 | 0,998130 |
| 3 | 0,03 | −6,144944 | −0,1859416 | 0,9962706 |
| 126 | 1,26 | 3,929768 | −0,0337729 | −0,6203322 |
Siehe Zahlenwerte im letzten Bild für und .
Partikuläre Lösung der GDGL eines senkrecht schwingenden Federpendels mit Eingangssignal u(t) > 0 ohne Anfangswerte[Bearbeiten | Quelltext bearbeiten]
Für die partikuläre Lösung der GDGL des Federpendels sind folgende rekursive Berechnungen nach dem Signalflussplan erforderlich:
- Die Eingangsgröße wird für einen normierten Sprung gewählt.
- . Diese bewerteten Koeffizienten wirken als Eingangsgröße auf
- Differenzengleichung des ersten I-Gliedes:
- . Der Ausgangswert des ersten Integrators ist der Eingangswert des zweiten Integrators. ()
- Differenzengleichung des zweiten I-Gliedes:
- . Der Ausgangswert des zweiten Integrators ist das Ergebnis einer Berechnungszeile. ()
- Die erste Berechnungszeile für enthält die Anfangswerte der Integratoren und der Differenzengleichungen. Alle übrigen Gleichungen in dieser Zeile haben den Wert Null.
Das Ergebnis der numerischen Berechnung ist eine spiegelbildliche Darstellung des Verlaufs von der homogenen Lösung für die gewählten Daten. Das System startet bei gedämpft schwingend und nähert sich asymptotisch nach genügend langer Zeit dem Wert 1.
Die Gesamtlösung der GDGL der gewählten Daten lautet für alle Folgen .
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Jürgen Koch, Martin Stämpfle / Mathematik für das Ingenieurstudium. Karl Hanser Verlag München. 4. Auflage 2018. ISBN 978-3-446-45166-7
- Bernd Girod, Rudolf Rabenstein, Alexander Stenger: Einführung in die Systemtheorie, Signale und Systeme in der Elektrotechnik und Informationstechnik. 4. Auflage. Teubner-Verlag, 2007, ISBN 978-3-8351-0176-0.
- Jan Lunze: Regelungstechnik 1: Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. 7. Auflage. Springer, 2008, ISBN 3-540-68907-9.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6.
- Rolf Unbehauen: Systemtheorie Band 1. 8. korr. Auflage, Oldenbourg 2002, ISBN 3-486-25999-7.
- Günter Ropohl, Eine Systemtheorie der Technik – Zur Grundlegung der allgemeinen Technologie, Carl Hanser Verlag 1979, ISBN 3-446-12801-8.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Prof. Dr.-Ing. O. Sawodny, Universität Stuttgart, „Systemdynamische Grundlagen der Regelungstechnik“.
- ↑ Prof. M. Ottens, FH Berlin, Vorlesungsmanuskript: „Grundlagen der Systemtheorie“.
- ↑ Fachbuch: Autor: Jan Lunze / Regelungstechnik 1, 5. Auflage, Springer-Verlag. Siehe Kapitel: Nichtlineare Regelungen, Unterkapitel: „Definition der Nichtlinearität“.
- ↑ Fachbuch: Autor Jürgen Koch, Martin Stämpfle / Mathematik für das Ingenieurstudium. Karl Hanser Verlag München. 4. Auflage. Siehe: Hauptkapitel „Gewöhnliche Differenzialgleichungen“.
- ↑ Fachbuch: Autor Holger Lutz / Wolfgang Wendt: Taschenbuch der Regelungstechnik, Verlag: Europa-Lehrmittel, 12. Auflage. Siehe Kapitel: „Übertragungsfunktionen von Übertragungselementen“.
- ↑ Fachbuch: Autor Jan Lunze: Regelungstechnik 1, 5. Auflage, Springer-Verlag. Siehe Kapitel: „Zustandsraumdarstellung linearer Systeme“.
- ↑ Fachbuch: Autor Jürgen Koch, Martin Stämpfle / Mathematik für das Ingenieurstudium. 4. Auflage, Karl Hanser Verlag München. Siehe: Hauptkapitel: „Numerische Verfahren“, Unterkapitel: „Polygonzugverfahren“.
- ↑ Fachbuch: Autor Jürgen Koch, Martin Stämpfle / Mathematik für das Ingenieurstudium. 4. Auflage, Karl Hanser Verlag München. Siehe: Kapitel: „Schwingungsdifferenzialgleichungen“.
- ↑ Fachbuch: Autor Holger Lutz / Wolfgang Wendt: Taschenbuch der Regelungstechnik, Verlag: Europa-Lehrmittel, 12. Auflage. Siehe Hauptkapitel: „Proportionalelemente mit Verzögerung“, Unterkapitel: „PT2-Element mit Verzögerung 2. Ordnung“.






















![{\displaystyle y(t)=K\cdot [1+{\frac {1}{T_{2}-T_{1}}}({T_{1}\cdot e^{-{\frac {t}{T_{1}}}}}-{T_{2}\cdot e^{-{\frac {t}{T_{2}}}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9102e78e41853c2acfe27fc8711813d9fcb2f5e)


















































![{\displaystyle t_{(k=126)}=1{,}26\ [sec]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfbc0aba78eea3d4cb9e0b5f83fa4ce10db07925)






