Hyperbolische Geometrie

Modell einer Parkettierung einer Ebene mit Quadraten. An den Ecken treffen dabei mehr als vier zusammen (je nach Größe, hier fünf).

Die hyperbolische Geometrie als Beispiel für eine nichteuklidische Geometrie erhält man, wenn man zu den Axiomen der absoluten Geometrie anstelle des Parallelenaxioms, das die euklidischen Geometrien kennzeichnet, das diesem widersprechende „hyperbolische Axiom“ hinzunimmt. Das hyperbolische Axiom besagt, dass es zu einer Geraden g und einem Punkt P (der nicht auf g liegt) nicht wie in der euklidischen Geometrie nur genau eine, sondern mindestens zwei Geraden (h und i) gibt, die durch P gehen und zu g parallel sind. Dass zwei Geraden „parallel“ zueinander sind, bedeutet hier aber lediglich, dass sie in derselben Ebene liegen und keine gemeinsamen Punkte haben, nicht dass sie überall den gleichen Abstand haben (h und i haben nur einen gemeinsamen Punkt P).

Es lässt sich zeigen, dass es dann zu einer beliebigen Geraden g durch jeden Punkt außerhalb von g unendlich viele Nichtschneidende („Parallelen“) gibt, die in der durch den Punkt und die Gerade bestimmten Ebene liegen. Zwei davon sind in einer Grenzlage und heißen grenzparallel (auch: horoparallel) zur Geraden, während die restlichen Geraden überparallel (auch: hyperparallel) genannt werden.

Modelle

Es gibt verschiedene Modelle, wie die hyperbolische Ebene in die euklidische Ebene eingebettet werden kann. Die meisten davon lassen sich für höhere Dimensionen verallgemeinern.

Alle Modelle stellen die gleiche abstrakte hyperbolische Geometrie dar. Es ist daher möglich, zwischen diesen Modellen umzurechnen. Aussagen in rein hyperbolischer Geometrie sind vom verwendeten Modell unabhängig.

Kleinsches Kreisscheibenmodell

In diesem von Eugenio Beltrami und Felix Klein entwickelten Modell gilt:

• Die hyperbolische Ebene wird durch eine offene Kreisscheibe modelliert.
• Hyperbolische Geraden werden durch Sehnen modelliert.
• Längen werden durch eine spezielle Distanzfunktion definiert (auch die Winkel sind verschieden von den euklidischen Werten).

Dieses Modell ist auch unter dem Namen Bierdeckelgeometrie bekannt.

Distanzfunktion

Abstand zweier Punkte in einer hyperbolischen Geometrie

Sind A und B zwei Punkte der Kreisscheibe, so trifft die durch A und B verlaufende Sehne den Kreis in zwei Punkten R und S. Der hyperbolische Abstand von A und B wird nun mit Hilfe des Doppelverhältnisses $(A,B,R,S)$ definiert:

$d(A,B)=\frac{1}{2} \ln (A,B,R,S) = \frac{1}{2} \ln\frac{\overline{RA}\cdot\overline{SB}}{\overline{RB} \cdot \overline{SA}}$.

Poincarésches Kreisscheibenmodell

Bei dem auf Beltrami zurückgehenden Kreisscheibenmodell von Henri Poincaré gilt:

• Die hyperbolische Ebene wird durch eine offene Kreisscheibe (meist den Einheitskreis) modelliert.
• Hyperbolische Geraden werden durch Kreisbögen (und Durchmesser), die auf dem Rand senkrecht stehen, modelliert.
• Die hyperbolische Winkelmessung entspricht der euklidischen Winkelmessung, wobei der Winkel zwischen zwei Kreisbögen über deren Tangenten am Schnittpunkt bestimmt wird.
• Die hyperbolische Längenmessung erfolgt durch eine spezielle Distanzfunktion.

Distanzfunktion

Seien A und B zwei Punkte der Kreisscheibe. Fasst man die Ebene als komplexe Zahlenebene auf, so entsprechen den Punkten A, B komplexe Zahlen a, b. Der hyperbolische Abstand von A und B wird nun mit Hilfe dieser komplexen Zahlen definiert:

$d(A,B)= arcosh(1+2 \frac{\lVert a-b \rVert^2}{(1-\lVert a \rVert^2)(1-\lVert b \rVert^2)})$

Poincarésches Halbebenenmodell

Bei dem auf Beltrami zurückgehenden Halbebenenmodell von Henri Poincaré gilt:

• Die hyperbolische Ebene wird durch die obere Halbebene (y>0) modelliert.
• Hyperbolische Geraden werden durch Kreisbögen (und Halbgeraden) modelliert, die auf der x-Achse senkrecht stehen.
• Die hyperbolische Winkelmessung entspricht der euklidischen Winkelmessung, wobei der Winkel zwischen zwei Kreisbögen über deren Tangenten am Schnittpunkt bestimmt wird.

Distanzfunktion

Der Abstand zwischen zwei Punkten er oberen Halbebene wird mit der folgenden Formel berechnet:

$\operatorname{d} (\langle x_1, y_1 \rangle, \langle x_2, y_2 \rangle) = \operatorname{arcosh} \left( 1 + \frac{ {(x_2 - x_1)}^2 + {(y_2 - y_1)}^2 }{ 2 y_1 y_2 } \right) \,.$

Hyperboloid-Modell

Das auf Poincaré zurückgehende Hyperboloidmodell bettet die hyperbolische Ebene in den dreidimensionalen Minkowskiraum ein.

Erlanger Programm

→ Hauptartikel: Erlanger Programm

Im Sinne von Felix Kleins Erlanger Programm ist hyperbolische Geometrie die Geometrie von

$(O(n,1),O(n)\times O(1))$.

Das Beltrami-Klein-Modell zeigt, dass man hyperbolische Geometrie als Teil der projektiven Geometrie auffassen kann.

Dreieck

Dreieck im hyperbolischen Raum

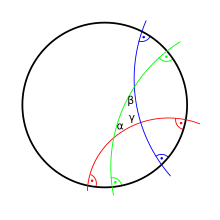
In der hyperbolischen Geometrie ist die Winkelsumme in einem Dreieck immer kleiner als π (180 Grad; bzw. zwei Rechte, wenn man das Winkelmaß vermeiden will). Für sehr große Dreiecke kann sie beliebig klein werden. Die Fläche des Dreiecks wird nach Johann Heinrich Lamberts Formel berechnet:

$\pi - ( \alpha + \beta + \gamma ) = C\,\Delta$

Wobei α, β und γ die jeweiligen Winkel, Δ die Fläche und die Konstante C ein Skalierungsfaktor ist. Der Skalierungsfaktor C ist abhängig vom verwendeten Einheitensystem und im Grunde gleich 1 zu setzen. Ist der Faktor C negativ, spricht man von einer (positiven) Gaußschen Krümmung. Analog dazu definierte Thomas Harriot zuvor im Jahr 1603 die Formel

$\Delta = R^2 \,(\alpha + \beta + \gamma - \pi)$

für die Fläche eines Dreiecks auf einer Kugeloberfläche, das von Kreisen mit demselben Radius wie die Kugel gebildet wird. Hiebei gilt der Zusammenhang

$C = -\frac{1}{R^2}$.

Da für die hyperbolische Geometrie ein positiver Wert für C erforderlich ist, muss es sich bei R aufgrund von

$R = (-C)^{-\frac{1}{2}}$

um einen imaginären Radius handeln.

Siehe auch

• Elliptische Geometrie
• Nikolai Lobatschewski
• János Bolyai
• Felix Klein
• Giovanni Girolamo Saccheri und Saccheri-Viereck

Literatur

• Norbert A'Campo, Athanase Papadopoulos: Notes on hyperbolic geometry. In: Strasbourg Master class on Geometry. European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-105-7, S. 1-182, doi:10.4171/105. (IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18)
•  Jeremy Gray: Ideas of Space: Euclidean, Non-Euclidean, and Relativistic. 2 Auflage. Oxford University Press, Oxford 1989, ISBN 9780198539353.
• Marvin Jay Greenberg: Euclidean & Non-Euclidean Geometries: Development and History. W. H. Freeman, 1993, ISBN 0-7167-2446-4.
•  Benno Klotzek: Euklidische und nichteuklidische Elementargeometrien. 1 Auflage. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0.
• Nikolai I. Lobachevsky: Pangeometry, Edited and translated by Athanase Papadopoulos, Heritage of European Mathematics. Vol. 4, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-087-6.
• Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. I, European Mathematical Society (EMS), Zürich 2007, ISBN 978-3-03719-029-6, doi:10.4171/029. (IRMA Lectures in Mathematics and Theoretical Physics 11)
• Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. II, European Mathematical Society (EMS), Zürich 2009, ISBN 978-3-03719-055-5, doi:10.4171/055. (IRMA Lectures in Mathematics and Theoretical Physics 13)
• Athanase Papadopoulos (Hrsg.): Handbook of Teichmüller theory. Vol. III, European Mathematical Society (EMS), Zürich 2012, ISBN 978-3-03719-103-3, doi:10.4171/103. (IRMA Lectures in Mathematics and Theoretical Physics 19)