Jeans-Kriterium

Das Jeans-Kriterium der Sternentstehung (nach James Jeans), auch Jeanssches Kriterium, besagt, dass eine kosmische Gaswolke kollabiert und aus ihr letztlich ein Stern entstehen kann, wenn ihre Masse größer als die Jeans-Masse ist. Handelt es sich bei der Gaswolke um eine protoplanetare Scheibe, so kann das Jeans-Kriterium auch für die Entstehung von Gasplaneten herangezogen werden.
Unter irdischen Bedingungen breiten sich Gase aufgrund der kinetischen Energie der Moleküle und ihrer damit verbundenen Kollisionen in dem zur Verfügung stehenden Raum gleichmäßig aus. Im freien Weltall dagegen werden größere Ansammlungen von Gasen durch ihre Schwerkraft zusammengehalten und sind deswegen räumlich begrenzt. Nach Überschreiten der Jeans-Masse zieht sich die Wolke immer weiter zusammen, bis ein neuer Gleichgewichtszustand erreicht wird (Sternentstehung).
Berechnung bzw. Abschätzung der Jeans-Masse[Bearbeiten | Quelltext bearbeiten]
Die Jeans-Masse als minimale Grenzmasse lässt sich abschätzen zu:
mit
- einem numerischen Vorfaktor , der von der Abschätzung und ihrer Genauigkeit abhängt
- weiteren Variablen, die im Folgenden erläutert werden.

Es wird eine kugelförmige Gaswolke der Masse , der homogenen Dichte , dem daraus zu berechnenden Radius und der Temperatur angenommen. Auf die Gaswolke wirken keine äußeren Kräfte, sie rotiert nicht, und das Gas verhält sich wie ein ideales Gas.
Die Wolke beginnt zu kollabieren, falls die zusammenziehenden Gravitationskräfte größer sind als die stabilisierende Kraft des Gasdruckes (Jeans-Kriterium). Dieser Zustand ist erreicht, wenn die Masse der Gaswolke bei einer bestimmten Dichte und Temperatur die zugehörige Jeans-Masse überschreitet. Sie kann sowohl über das Gleichgewicht der Drücke als auch über das der Energien ermittelt werden.
Über den Gleichgewichtsdruck[Bearbeiten | Quelltext bearbeiten]
Bei Gleichgewicht der Drücke im Zentrum der Wolke gilt:
Aus der idealen Gasgleichung
und dem Gravitationsdruck im Zentrum einer Kugel folgt
mit
- dem Druck
- dem Volumen
- der Zahl der Gasmoleküle
- der Boltzmann-Konstanten
- der absoluten Temperatur
- der Masse des einzelnen Gasmoleküls
- der Gravitationskonstanten .
Daraus ergibt sich:[1]
- .
Der numerische Vorfaktor ist hier und beschreibt den Zustand im Zentrum der Wolke.
Über das Energiegleichgewicht[Bearbeiten | Quelltext bearbeiten]
Bei dem Ansatz über das Energiegleichgewicht steht die kinetische Energie nach Verwendung des Virialsatzes zur gravitativen Bindungsenergie der Gaswolke wie folgt:
bzw. mit :
Die Auflösung nach führt zu folgender kritischen Masse:
Also ein numerischer Vorfaktor , der für eine einheitliche Temperatur der Wolke gilt.
Über die Schallgeschwindigkeit[Bearbeiten | Quelltext bearbeiten]
Die von Jeans,[2] gefundene Masse geht von der Schallgeschwindigkeit im einatomigen Gas mit dem Isentropenexponenten aus.
Mit der Jeans-Länge
ergibt sich die Jeans-Masse
- .
Der Faktor π/6 entspricht dabei dem Volumen einer Kugel in einem Würfel mit gegebener Kantenlänge λ.
Daraus ergibt sich der Vorfaktor mit
- .
Einfluss von Dichte und Temperatur[Bearbeiten | Quelltext bearbeiten]
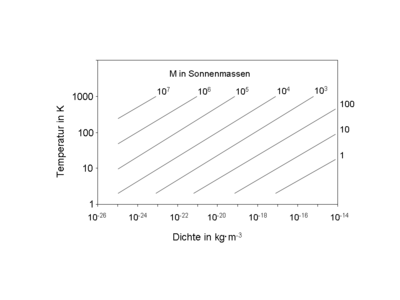
Wie sich aus den Formeln ablesen lässt, ist die Jeans-Masse für kalte Gaswolken kleiner als für heiße, dafür aber bei niedrigen Gasdichten höher. Das nebenstehende Diagramm gibt diese Abhängigkeit verschiedener Jeans-Massen von der Dichte und der Temperatur wieder. Die Jeans-Masse ist als Vielfaches der Sonnenmasse angegeben, als Gas wurde einatomiges Wasserstoffgas als häufigstes Element im Universum gewählt (Masse pro Atom: µ ≈ 1.67e-27 kg). Die Berechnung erfolgte wie oben ausgeführt über das Druckgleichgewicht; die Berechnung über das Energiegleichgewicht würde zu einem leicht unterschiedlichen Ergebnis führen, allerdings sind beide Ansätze stark vereinfachte Näherungen.
Ablese-Beispiel: Eine Wolke aus einatomigem Wasserstoffgas von 10 Sonnenmassen und einer Dichte von 10−17kg ⋅m−3 kollabiert bei einer Temperatur von ≤ 10 K. Zur Veranschaulichung hätte eine solche Wolke etwa 6000 Atome pro cm³ und einen Durchmesser von 1,65 Lichtjahren (1.56e13 Kilometer).
Literatur und Quellen[Bearbeiten | Quelltext bearbeiten]
- Bradley W. Carroll, Dale A. Ostlie: An introduction to Modern Astrophysics. 1996, ISBN 0-321-21030-1, S. 449.
- Hermann Kolanoski: Einführung in die Astroteilchenphysik. (PDF; 13,8 MB) Abgerufen am 21. Juli 2013.
- Malcolm S. Longair: Galaxy Formation. Springer, Berlin, 1998, ISBN 3-540-63785-0. (Astronomy and Astrophysics Library).
- Roman Sexl, Hannelore Sexl: Weiße Zwerge – Schwarze Löcher. Einführung in die relativistische Astrophysik. 2. erweiterte Auflage. Vieweg Verlag, Braunschweig 1999, ISBN 3-528-17214-2 (Vieweg-Studium – Grundkurs Physik).
- Albrecht Unsöld, Bodo Baschek: Der neue Kosmos. 4. völlig neubearbeitete Auflage. Springer, Berlin 1988, ISBN 3-540-18171-7.




























