Kongruenzgenerator

Die Kongruenzgeneratoren bilden eine Klasse von Algorithmen, die zufällig aussehende Zahlenfolgen erzeugen. Die dadurch erzeugten Zahlen nennt man Pseudozufallszahlen, da sie deterministisch erzeugt werden und somit nicht wirklich zufällig sind. Kongruenzgeneratoren sind die bekanntesten und meistverwendeten rekursiven arithmetischen Zufallszahlengeneratoren.

Allgemeiner Kongruenzgenerator

Ein Kongruenzgenerator wird durch folgende Parameter definiert:

• Anzahl $n \in \mathbb{N}^+$ der Zustandswerte
• Modul $m \in \{2, 3, 4, \ldots\}$
• Faktoren $a_1, \ldots, a_n \in \left\{ 0, \ldots, m-1 \right\}$
• Inkrement $b \in \left\{ 0, \ldots, m-1 \right\}$
• Startwerte (Saat, engl. „Seed“) $y_1, \ldots, y_n \in \left\{ 0, \ldots, m-1 \right\}$

Für $i > n$ setzt man nun

$y_i = \left( \left(\sum_{k=1}^{n} a_k y_{i-k} \right) + b \right) \, \bmod \, m$. Dabei bezeichnet $\mod$ den Divisionsrest; siehe Modulo.

Die so berechneten $y_i$ werden als Zufallszahlen verwendet. Braucht man reelle Zufallszahlen im Intervall $[0, 1)$, so kann man dafür die Näherung

$u_i := \frac{y_i}{m}$

verwenden, falls der Modul $m$ groß genug ist, um eine ausreichend feine Unterteilung zu ergeben.

Der Zustand des Generators vor der Erzeugung von $y_i$ wird durch die Werte $y_{i-n}, \ldots, y_{i-1}$ gegeben. Dieser Zustand legt (bei gegebenen $n,m,a_k,b$) alle folgenden Zufallszahlen fest, da die nächste Zufallszahl und der nächste Zustand durch den aktuellen Zustand determiniert werden. Es gibt $m^n$ mögliche Zustände, und deshalb muss spätestens nach $m^n$ Schritten ein früherer Zustand wiederholt werden. Der Kongruenzgenerator erzeugt somit eine periodische Folge von Zahlen, wobei die Periodenlänge auch wesentlich kleiner als $m^n$ sein kann. Im Extremfall ist sie 1, und der Generator erzeugt immer die gleiche „Zufallszahl“. Bei der Festlegung der Parameter kommt es somit unter anderem darauf an, eine ausreichende Periodenlänge sicherzustellen.

Linearer Kongruenzgenerator

Mit $n = 1$ erhält man den Sonderfall eines linearen Kongruenzgenerators. Bei $b = 0$ wird er als multiplikativer Kongruenzgenerator bezeichnet, und für andere $b$ als gemischter linearer Kongruenzgenerator.

Letzterer wird häufiger verwendet und hat vier natürliche Zahlen als Parameter:

• Modul $m \in \{2, 3, 4, \ldots\}$
• Faktor $a \in \{1, \ldots , m-1\}$
• Inkrement $b \in \{1, \ldots , m-1\}$
• Startwert $y_1 \in \{0, \ldots , m-1\}$

Aus dem Startwert werden dann die weiteren Werte nach folgender Formel (mit $i \ge 2$) berechnet:

$y_i = (a y_{i-1} + b) \ \bmod \ m$

Der lineare Kongruenzgenerator wurde 1949 von D. H. Lehmer eingeführt. Er wird in den Laufzeitbibliotheken verschiedener Programmiersprachen zur Erzeugung von Pseudozufallszahlen verwendet. In der Kryptographie dagegen kommt er nicht zum Einsatz, da man schon aus wenigen Werten der erzeugten Zahlenfolge die Parameter $a$ und $b$ und damit die vollständige Zahlenfolge berechnen kann.

Periodenlänge

Lineare Kongruenzgeneratoren erreichen nach dem Satz von Knuth genau dann ihre maximal mögliche Periodenlänge $m$, wenn die folgenden Voraussetzungen erfüllt sind:

• Das Inkrement $b$ ist zum Modul $m$ teilerfremd.
• Jeder Primfaktor von $m$ teilt $a-1$.
• Wenn $m$ durch 4 teilbar ist, dann auch $a-1$.

In diesem Fall erzeugt der Generator jede Zahl von 0 bis $m-1$ genau einmal und beginnt dann wieder von vorn. Er liefert also eine pseudozufällige Permutation dieser Zahlen. Der Startwert $y_1$ kann dann jede Zahl aus dieser Menge sein.

Der multiplikative Kongruenzgenerator (mit $b=0$) muss somit eine Periodenlänge kleiner als $m$ haben. Der Satz von Carmichael besagt: bei gegebenem $m$ ist seine Periodenlänge genau dann maximal, wenn gilt:

• $y_1$ ist zu $m$ teilerfremd,
• $a$ ist ein primitives Element modulo $m$.

Für einige Sonderfälle von $m$ können die primitiven Elemente modulo $m$ leicht bestimmt werden:

• Ist $m$ eine Zweierpotenz $\ge 16$, dann muss $a$ mod 8 den Rest 3 oder 5 liefern. Die Periodenlänge ist dann $m/4$, und der Startwert $y_1$ muss ungerade sein. Es gibt zwei Perioden, die jeweils die Hälfte der ungeraden Zahlen von $1$ bis $m-1$ umfassen.
• Wenn m eine Primzahl $\ge 3$ ist, dann muss für alle Primfaktoren $q$ von $m-1$ gelten:
  $a^{(m-1)/q} \ \bmod \ m \ne 1$. Dann beträgt die Periodenlänge $m - 1$. Der Startwert $y_1$ darf nicht Null sein.

Mängel der erzeugten Zahlen

Der lineare Kongruenzgenerator liefert keine vollkommen zufällig erscheinenden Zahlen. Man kann nachweisen, dass eine Abhängigkeit von aufeinanderfolgenden Zahlen besteht.

Teilperiode

Oft wählt man $m = 2^e$, wobei $e$ die Wortlänge des Rechners in Bit ist, denn dann muss man die Modulo-Division nicht explizit berechnen. Sie ergibt sich von selbst durch das Abschneiden der Überlauf-Bits. In diesem Fall verhalten sich die $x$ niederwertigsten Bits der Zustandszahl $y_i$ wie ein Generator mit dem Modul $2^x$. Diese Bits wiederholen sich also spätestens nach $2^x$ Schritten. Dies bedeutet insbesondere, dass das niederwertigste Bit bestenfalls die Periode 2 besitzt, also regelmäßig zwischen 0 und 1 wechselt. Beim multiplikativen Kongruenzgenerator ist es sogar konstant.

Allgemein gilt für alle linearen Kongruenzgeneratoren: wenn $d$ ein Teiler des Moduls $m$ ist, dann ergibt $y_i \ \bmod \ d$ eine Zahlenfolge mit der Periode $o \le d$:

für ein $o \in \{1, \ldots, d\}$ gilt: $\forall i: y_{i+o} \equiv y_i \ ( \bmod \ d)$.

Wenn der Generator nach dem Satz von Knuth die Periode $m$ hat, dann beträgt die Länge $o$ der Teilperiode genau $d$ für alle Teiler $d$ von $m$.

Wegen dieses Teilperioden-Verhaltens ist es ungünstig, Zufallszahlen $r_i \in \{0, \ldots, k-1\}$ durch $r_i := y_i \ mod \ k$ zu gewinnen, wenn $k$ und $m$ nicht teilerfremd sind. Dann würde der Divisionsrest $r_i \ \bmod \ d$ für eine Zahl $d$, die $k$ und $m$ teilt, eine Periode der Länge höchstens $d$ durchlaufen. Wenn man z. B. einen sechsseitigen Würfel simulieren will und $m$ gerade ist, dann liefert $r_i := y_i \ mod \ 6$ Zahlen, die abwechselnd gerade und ungerade sind.

Mögliche Abhilfe:

• Man verwendet einen multiplikativen Kongruenzgenerator mit einer großen Primzahl als Modul $m$ und setzt $r_i := y_i \ \bmod \ k$. Dann sind aber die $r_i$ nicht gleichverteilt, es sei denn, $m-1$ ist ein Vielfaches von $k$. Wenn $k \ll m$ ist, kann man dieses Problem oft vernachlässigen.
• Wenn $m = 2^e$ ist: die $y_i$ um $e-f$ Bit nach rechts schieben, um die höchstwertigen Bits zu verwenden: $r_i := \lfloor y_i / 2^{e-f} \rfloor$ (wobei $2^f$ die kleinste Zweierpotenz $\ge k$ ist). Wenn das Ergebnis $r_i \ge k$ ist, wird es verworfen und neu erzeugt. Diese Methode liefert gleichverteilte Ergebnisse.

Hyperebenen-Verhalten

„Hyperebenenverhalten“ eines linearen Kongruenzgenerators in drei Dimensionen

Gemischter Kongruenzgenerator: $x_{n+1} = 24298x_n + 99991 mod 199017$. Dieser Generator wird im TI-59 von Texas Instruments verwendet. Gezeigt werden überlappende Tripel, dh., $(x_1,x_2,x_3)$, $(x_2,x_3,x_4)$, $(x_3,x_4,x_5)$, etc. Ohne Überlappungen bliebe nur jede dritte Ebene übrig.

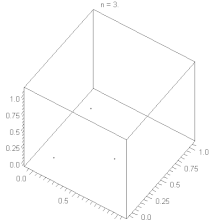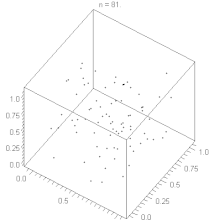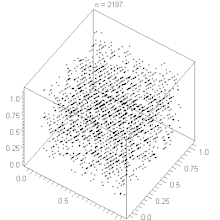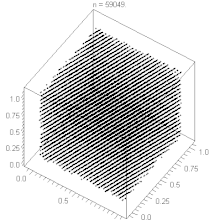
Der lineare Kongruenzgenerator weist ein Hyperebenen-Verhalten auf, siehe Satz von Marsaglia. Durch geeignete Wahl der Parameter $m$, $a$ und $b$ kann man das Verhalten des Generators optimieren und eine große Zahl von Hyperebenen erreichen. Bei gegebenem $m$ kann man $a$ nach folgenden Faustregeln bilden:

• $a$ sollte weder zu groß noch zu klein sein, etwa: $0{,}01 \cdot m < a < 0{,}99 \cdot m$
• $a$ sollte möglichst zufällig gewählt werden, also nicht in dualer oder dezimaler Darstellung eine „runde“ Zahl sein.
• Beim gemischten linearen Kongruenzgenerator sollte die Potency möglichst groß sein. Sie ist der minimale Wert $s$, für den $(a-1)^s$ ein Vielfaches von $m$ ist. Donald Knuth empfiehlt, dass die Potency mindestens 5 sein sollte. Wenn $m = 2^e$, dann sollte $a \ \bmod \ 8 = 5$ sein, um die maximal mögliche Potency $\lceil e/2 \rceil$ zu erhalten.

Wenn man sichergehen will, dass der Generator gute Zufallszahlen erzeugt, sollte man sich nicht allein auf diese Faustregeln verlassen, sondern den Generator mit dem Spektraltest prüfen.

Wegen des Hyperebenen-Verhaltens greift man statt auf den linearen Kongruenzgenerator gelegentlich auf den inversen Kongruenzgenerator zurück, der dieses Problem nicht aufweist. Allerdings erfordert er einen höheren Rechenaufwand. Er ist kein Spezialfall des allgemeinen Kongruenzgenerators.

Fibonacci-Generator

Ein Fibonacci-Generator ist ebenfalls ein Kongruenzgenerator (mit $n=2$, $b=0$ und $a_1 = a_2 = 1$) und besteht aus folgenden Komponenten:

• Modul $m \in \{2, 3, 4, \ldots\}$
• Startwerte $y_1, y_2 \in \left\{ 0, \ldots, m-1 \right\}$

Mit folgender Bildungsregel werden die Pseudozufallszahlen erzeugt:

$y_i = ( y_{i-1} + y_{i-2} ) \ \bmod \ m \quad (\mbox{mit} \ i \ge 3)$

Eine Eigenschaft ist es, dass die Fälle $y_{i-1} < y_{i+1} < y_i$ bzw. $y_i < y_{i+1} < y_{i-1}$ nie auftreten. Fibonacci-Generatoren sind daher als Pseudozufallszahlengeneratoren wenig geeignet. Das gilt insbesondere für mathematische Objekte, zu deren Erzeugung mehr als zwei Zufallszahlen erforderlich sind. Würde man beispielsweise damit versuchen, eine zufällige Punktewolke in einem Würfel zu generieren, so kämen alle Punkte auf zwei Ebenen zu liegen.

Verzögerter Fibonacci-Generator

Das Prinzip des Fibonacci-Generators kann aber verallgemeinert werden, indem man nicht die beiden letzten, sondern weiter zurückliegende Zustandswerte $y_i$ zur Erzeugung der neuen Zufallszahl verwendet. Dies ergibt einen verzögerten (engl. 'lagged') Fibonacci-Generator:

$y_i = ( y_{i-B} + y_{i-A} ) \ \bmod \ m \quad \mbox{mit} \; A,B \in \mathbb{N}^+, \ A > B; \quad i > A$

mit den Startwerten $y_1, \ldots,y_A \in \left\{ 0, \ldots, m-1 \right\}$

Dann ist also $n=A$ und $a_A = a_B = 1$, die übrigen $a_k$ sind Null. Dabei wählt man in der Regel $m$ gerade und $A$ und $B$ so, dass das Polynom in x

$x^A + x^B + 1$

ein primitives Polynom modulo 2 ist. Dann beträgt die Periodenlänge des Generators mindestens $2^A - 1$.

Die folgende Tabelle gibt einige Wertepaare für $A$ und $B$ an, die diese Bedingung erfüllen:

A	2	31	55	73	98	100	135	258	607	3217	23209
B	1	13	24	25	27	37	22	83	273	576	9739

$x^A + x^B + 1$ ist genau dann ein primitives Polynom modulo 2, wenn dies für $x^A + x^{A-B} + 1$ gilt. Somit kann man statt $B$ immer auch $A-B$ verwenden.

Dieser Generator wird auch praktisch eingesetzt. Er liefert aber ebenfalls keine vollkommen zufällig erscheinenden Zahlen. Das Problem des einfachen Fibonacci-Generators wird nur verlagert: man hat niemals $y_{i-A} < y_i < y_{i-B}$ oder $y_{i-B} < y_i < y_{i-A}$. Außerdem gibt es noch weitere Mängel.

Als Abhilfe wurde vorgeschlagen, immer nur $A$ aufeinanderfolgende Zahlen zu verwenden, und dann die nächsten $4 A$ bis $10 A$ Zahlen zu verwerfen. Dies funktioniert gut, aber um den Preis eines 5 bis 11 mal höheren Rechenaufwands. Der von Donald Knuth vorgeschlagene Generator ranarray arbeitet auf diese Weise. Bei ihm ist $A = 100$ und $B = 37$, und von 1009 aufeinanderfolgenden Zahlen wird immer nur ein Block von 100 Zahlen verwendet.

Um die Periode $2^A - 1$ sicherzustellen, kommt es nur auf das jeweils niederwertigste Bit in den Zustandswerten $y_i$ an, also darauf, ob sie gerade oder ungerade sind. Man kann die höherwertigen Bits beliebig modifizieren, um die Qualität der erhaltenen Zufallszahlen zu verbessern. Beispielsweise:

$y_i = (y_{i-A} + y_{i-B} + f(y_{i-C})) \ \bmod \ m; \quad f: \{0, \ldots, m-1\} \rightarrow \{0, 2, 4, 6, \ldots\}, \; C \in \{ 1, \ldots, n \}$

Andere

Man kann den verzögerten Fibonacci-Generator weiter verallgemeinern, indem man mehr als zwei Zustandswerte verarbeitet:

$y_i = ( \sum_{k \in M} y_{i-k} ) \ \bmod \ m \quad \mbox{mit} \quad M \subset \mathbb{N}^+$.

$n$ ist hier das größte Element in $M$. Um eine Periode von mindestens $2^n-1$ zu garantieren, muss auch hier das entsprechende Polynom

$\sum_{k \in M} x^k + 1$ oder gleichbedeutend das Polynom $x^n + \sum_{k \in M} x^{n-k}$

ein primitives Polynom modulo 2 sein (mit geradem Modul $m$). Ein so konstruierter Generator mit $|M| > 2$ liefert im Allgemeinen bessere Zufallszahlen als mit $|M| = 2$, aber wiederum um den Preis eines höheren Rechenaufwands.

Mit einer weiteren Verallgemeinerung kann man bei gegebenem $n$ die Periodenlänge vergrößern und wohl auch die Qualität der Zufallszahlen weiter verbessern. $p$ sei ein Primfaktor von $m$. für die Berechnungsvorschrift

$y_i = ( \sum_{k = 1}^{n} a_k y_{i-k} ) \ \bmod \ m$

werden die $a_k \in \{ 0, \ldots, m-1 \}$ derart gewählt, mit $a_n \not\equiv 0 (\bmod \ p)$, dass das Polynom in x

$x^n - \sum_{k=1}^{n} (a_k \ \bmod \ p) x^{n-k}$

ein primitives Polynom modulo p ist. Dann beträgt die Periodenlänge mindestens $p^n - 1$.
Der vorige Generator ergibt sich daraus mit $p = 2$ und $a_k \in \{ 0, 1 \}$ als Sonderfall, und $n=1; \ p=m$ liefert einen multiplikativen Kongruenzgenerator mit der Periodenlänge $p - 1$.

Das Polynom $f(x) = x^n - \sum_{k=1}^{n} a_k x^{n-k}$ ist ein primitives Polynom modulo p, wenn die folgenden Bedingungen erfüllt sind:

($\mbox{sei} \quad r = \frac{p^n-1}{p-1} \quad \mbox{und} \quad a = (-1)^{n-1} a_n$)

• $a$ ist ein primitives Element modulo p
• das Polynom $x^r$ ist kongruent zu $a$ (modulo $f(x)$)
• für alle Primfaktoren $q$ von $r$ ist der Grad des Polynoms $x^{r/q} \ \bmod \ f(x)$ positiv

Dabei wird Polynomarithmetik angewandt (siehe Polynome sowie Polynomdivision), und mit den Koeffizienten wird modulo $p$ gerechnet (sie sind Elemente des Restklassenrings $\Z / p \Z$).

Siehe auch

Zur Erklärung der Symbolik siehe den Artikel Modulo.

• Mersenne-Twister
• Blum-Blum-Shub-Generator

Einzelnachweise

Arithmetische Zufallszahlengeneratoren

Kongruenzgenerator (linearer, multiplikativer, gemischt linearer, Fibonacci-Generator) | Inverser Kongruenzgenerator | Blum-Blum-Shub-Generator | KISS | Mersenne-Twister | Multiply-with-carry | WELL | Xorshift