Weierstraß-Funktion
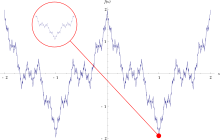
In der Mathematik bezeichnet man als Weierstraß-Funktion ein pathologisches Beispiel einer reellwertigen Funktion einer reellen Variablen. Diese Funktion hat die Eigenschaft, dass sie überall stetig, aber nirgends differenzierbar ist. Sie ist nach ihrem Entdecker[1] Karl Weierstraß benannt. Historisch gesehen liegt ihre Bedeutung darin, dass sie das erste befriedigende Beispiel für eine nirgends differenzierbare Funktion ist. Weierstraß war allerdings nicht der erste, der eine solche Funktion konstruierte. Bereits mehr als 30 Jahre zuvor hat Bernard Bolzano eine Funktion angegeben, die Bolzanofunktion, die nirgends differenzierbar, aber überall stetig ist.[2] Allerdings ist sein Beweis unvollständig und die Konstruktion wurde einer breiteren Fachöffentlichkeit nicht bekannt. Die überraschende Konstruierbarkeit einer solchen Funktion änderte die übliche Meinung, dass jede stetige Funktion, bis auf eine Menge isolierter Punkte, differenzierbar sei. Die Überraschung der damaligen Fachgemeinde drückt sich unter anderem darin aus, dass zu Beginn der Rezension der weierstraßschen Arbeit fast ausschließlich vom „Weierstraßschen Monster“ die Rede ist (siehe zur Geschichte dieser Funktion auch[3]).
Seinerzeit wurde intuitiv angenommen, dass eine stetige Funktion eine Ableitung besitzt oder dass die Menge der Punkte, in denen sie nicht differenzierbar ist, „klein“ in irgendeinem Sinne ist. Frühere Mathematiker, einschließlich Carl Friedrich Gauß, haben oft angenommen, dass das wahr ist, wie Weierstraß in seiner Arbeit ausführt. Das rührt aus der Schwierigkeit, eine stetige Funktion zu zeichnen oder darzustellen, deren Menge nicht differenzierbarer Punkte etwas anderes ist als eine endliche Menge von Punkten. Die Weierstraß-Funktion widerlegt diese intuitive Annahme für jede denkbare Bedeutung von „klein“.
Es gibt jedoch Klassen stetiger Funktionen, die sich „besser“ verhalten, zum Beispiel die Lipschitz-stetigen Funktionen, bei denen die Menge der nicht-differenzierbaren Punkte eine Lebesgue-Nullmenge sein muss. Wenn man eine stetige Funktion zeichnet, dann entsteht üblicherweise der Graph einer Funktion, die Lipschitz-stetig ist und andere gutartige Eigenschaften besitzt, die nicht auf allgemeine stetige Funktionen zutreffen.
Auch die weierstraßsche elliptische Funktion und die weierstraßsche sigma-, zeta- oder eta-Funktion werden manchmal als Weierstraß-Funktion bezeichnet.
Weierstraß-Funktionen[Bearbeiten | Quelltext bearbeiten]
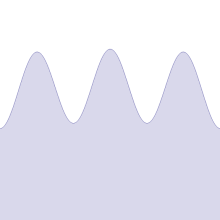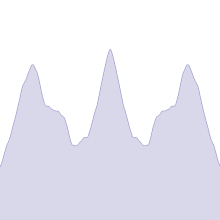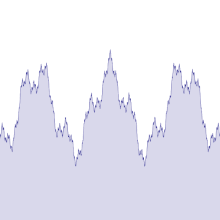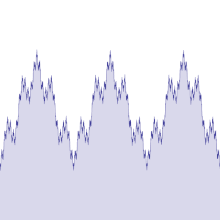
Es gibt verschiedene, ähnliche Definitionen einer Weierstraß-Funktion, die alle Reihen mit Winkelfunktionen sind.
Definition nach Weierstraß[Bearbeiten | Quelltext bearbeiten]
In Weierstraß’ Originalarbeit wurde die Funktion durch
mit und ungerade definiert, wobei zusätzlich
erfüllt sein muss. Diese Arbeit mit der Definition und dem Beweis, dass die Funktion nirgends differenzierbar ist, wurde am 18. Juli 1872 bei der Königlichen Akademie der Wissenschaften eingereicht.[4]
Definition nach Hardy[Bearbeiten | Quelltext bearbeiten]
Godfrey Harold Hardy zeigte 1916, dass die Funktion
unter den Annahmen , nirgends differenzierbar ist.[5]
Beispiele[Bearbeiten | Quelltext bearbeiten]
Eine oft verwendete Weierstraß-Funktion ist
- .
Anschaulich ist die Weierstraß-Funktion
Ihr Graph sieht „fast“ so aus wie der Graph der (differenzierbaren) Sinusfunktion. Sie wäre auch differenzierbar, wenn nur noch endlich viele Summanden hinzukämen. Durch jeweils den nächsten (viel kleineren) Summanden wird der Graph um ein winziges Stück verändert. Sie ist überall konvergent, stetig, aber man kann keine Tangenten zu ihr konstruieren, ist also nicht differenzierbar.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Beweis der Stetigkeit[Bearbeiten | Quelltext bearbeiten]
Für alle und gilt . Zudem ist die Reihe wegen konvergent. Dann folgt aus dem weierstraßschem Majorantenkriterium die (bezüglich ) gleichmäßige Konvergenz von . Da die einzelnen Partialsummen der Reihe stetige Funktionen sind und die Grenzfunktion einer gleichmäßig konvergenten Folge stetiger Funktionen wieder stetig sein muss, folgt daraus die behauptete Stetigkeit von .
Fraktale Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Die Weierstraß-Funktion kann vielleicht als eines der ersten Fraktale bezeichnet werden, obwohl dieser Begriff damals noch nicht verwendet wurde. Die Funktion ist auf jedem Niveau detailliert, so dass, wenn man ein Stück der Kurve vergrößert, es sich nicht fortschreitend einer geraden Linie nähert. Unabhängig davon, wie dicht man zwischen zwei Punkte geht, die Funktion ist auf keinem noch so kleinen Intervall monoton. In seinem Buch Die Geometrie der fraktalen Mengen beobachtet Kenneth Falconer, dass die Hausdorff-Dimension der klassischen Weierstraß-Funktion nach oben durch beschränkt ist, wobei und die Konstanten in der obigen Konstruktion sind.[6] Es dauerte jedoch über 30 Jahre, bis ein Beweis erbracht werden konnte, dass dieser Wert tatsächlich die exakte Hausdorff-Dimension darstellt.[7] Der Ausdruck Weierstraß-Funktion wird in der reellen Analysis oft verwendet, um irgendeine Funktion mit ähnlichen Eigenschaften und einer ähnlichen Konstruktion wie Weierstraß’ Originalbeispiel zu bezeichnen. Zum Beispiel kann die Kosinusfunktion in den unendlichen Reihen durch eine stückweise lineare „Zick-Zack-Funktion“ ersetzt werden.
Dichtheit nirgends differenzierbarer Funktionen[Bearbeiten | Quelltext bearbeiten]
Es gibt unendlich viele stetige, nirgends differenzierbare Funktionen; die Weierstraß-Funktion ist nur das klassische Beispiel, bei dem eine explizite Darstellung bekannt ist. Generell gilt:
- In der Topologie kann gezeigt werden, dass die Menge der nirgends differenzierbaren Funktionen auf dem Intervall dicht liegt im Vektorraum aller stetigen reellwertigen Funktionen auf dem Intervall mit der Topologie der gleichmäßigen Konvergenz.
- In der Maßtheorie zeigt sich zudem: Wenn der Raum mit dem klassischen Wiener-Maß ausgestattet ist, dann hat die Menge der Funktionen, die sogar in einem Punkt in differenzierbar sind, -Maß null. Dasselbe gilt, wenn man nur endlichdimensionale Teilmengen von betrachtet: Die nirgends differenzierbaren Funktionen bilden damit eine prävalente Untermenge von .
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Weierstrass Function (beschreibt eine andere Weierstraß-Funktion). In: MathWorld (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Karl Weierstraß: Abhandlungen aus der Functionenlehre. Julius Springer, Berlin 1886.
- ↑ Bernard Bolzano: Funktionenlehre. Hrsg.: K. Rychlik. Prag 1831.
- ↑ Klaus Volkert: Die Geschichte der pathologischen Funktionen - Ein Beitrag zur Entstehung der mathematischen Methodologie. In: Archive for History of Exact Sciences. Band 37, Nr. 3, doi:10.1007/BF00329901.
- ↑ Karl Weierstraß: Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzteren einen bestimmten Differentialquotienten besitzen. In: Mathematische Werke. Band 2. Mayer & Müller, Berlin 1895, S. 71–74 (Download bei archive.org).
- ↑ Godfrey Harold Hardy: Weierstrass's non-differentiable function. In: Trans. Amer. Math. Soc. Band 17, Nr. 3, 1916, S. 301–325, doi:10.1090/S0002-9947-1916-1501044-1.
- ↑ Kenneth Falconer: The geometry of fractal sets. Cambridge University Press, Cambridge, England 1985, S. 114, 149 (englisch).
- ↑ Weixiao Shen: Hausdorff dimension of the graphs of the classical Weierstrass functions. In: Mathematische Zeitschrift. Band 289, Nr. 1–2. Springer-Verlag, Juni 2018, ISSN 0025-5874, S. 223–266, doi:10.1007/s00209-017-1949-1, arxiv:1505.03986 (englisch).
![{\displaystyle [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94b820404eca2a458cb2c7d8c24be85fffccf90)

















![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle C([0,1];\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a116146f1e001bc816b3f1a2ef74896560a27fc1)
