Stabilitätsfunktion
Die Stabilitätsfunktion ist in der Numerik ein Hilfsmittel, um Lösungsverfahren für gewöhnliche Differentialgleichungen zu analysieren. Die einfache Testgleichung von Germund Dahlquist mit besitzt als Lösung die Exponentialfunktion . Bei den meisten Verfahren für gewöhnliche Differentialgleichungen kann man die berechnete Näherungslösung nach einem Zeitschritt mit einer Schrittweite ebenfalls als eine Funktion schreiben, die nur vom Produkt abhängt. Diese Funktion ist die Stabilitätsfunktion und wird oft mit bezeichnet. Durch einen Vergleich mit der Exponentialfunktion bekommt man grundlegende Informationen über das numerische Verfahren. So beziehen sich einige Stabilitätsbegriffe auf die Eigenschaften von .
Stabilitätsgebiet und Stabilitätsbegriffe
[Bearbeiten | Quelltext bearbeiten]Mit Hilfe der Stabilitätsfunktion lässt sich das Stabilitätsgebiet beschreiben und berechnen in der Form
Denn bei Einschrittverfahren gilt für die Näherungen zum Zeitpunkt die Beziehung und daher gilt
Wenn die ganze linke komplexe Halbebene umfasst, heißt das Verfahren A-stabil. Dann ist der Betrag von in der ganzen offenen linken Halbebene kleiner als 1. Besonders günstig für ein Verfahren ist es, wenn außerdem noch den Grenzwert 0 hat, wenn auf der reellen Achse gegen strebt, sodass sich also der Betrag von dort asymptotisch wie die Exponentialfunktion verhält. Dann heißt das Verfahren L-stabil.
Beispiel
[Bearbeiten | Quelltext bearbeiten]Das explizite Euler-Verfahren ergibt für die Testgleichung mit nach einem Schritt
- ,
also gilt für seine Stabilitätsfunktion . Sein Stabilitätsgebiet besteht daher aus allen komplexen Zahlen mit , was dem Inneren des Kreises mit Mittelpunkt und Radius in der komplexen Zahlenebene entspricht.
Für das implizite Euler-Verfahren folgt dagegen mit
- ,
also . Das Stabilitätsgebiet ist nun durch die Bedingung gegeben, die mit
gleichwertig ist, was dem Äußeren des Kreises mit Mittelpunkt und Radius entspricht. Es enthält daher die ganze offene linke Halbebene und somit ist das implizite Euler-Verfahren A-stabil. Wegen ist es sogar L-stabil.
Die Stabilitätsfunktion von Runge-Kutta-Verfahren
[Bearbeiten | Quelltext bearbeiten]Runge-Kutta-Verfahren sind vollständig durch die Koeffizienten aus ihrem Butcher-Tableau festgelegt. Bei der Testgleichung ist der Anfangswert und für die Stufen ergibt sich im ersten Zeitschritt
Dies ist ein quadratisches lineares Gleichungssystem für den Vektor in der Form mit dem Vektor Mit dessen Lösung bekommt man dann die Runge-Kutta-Näherung in der Form
Dies ist bei Runge-Kutta-Verfahren eine rationale Funktion, daher wird sie gerne mit bezeichnet.
Bei expliziten Runge-Kutta-Verfahren ist die Koeffizientenmatrix eine strikt untere Dreiecksmatrix, daher bricht die Neumann-Reihe von nach s Summanden ab und man bekommt
Daher ist die Stabilitätsfunktion eines expliziten Runge-Kutta-Verfahrens ein Polynom, solche Verfahren können nicht A-stabil sein.
Bei impliziten Runge-Kutta-Verfahren sind aber z. B. die Gauß-Legendre-Verfahren A-stabil. Die Stabilitätsfunktionen dieser speziellen Verfahren sind sogar sehr gute Approximationen an die Exponentialfunktion, nämlich die sogenannten Padé-Approximationen.
Die Stabilitätsfunktion von Mehrschrittverfahren
[Bearbeiten | Quelltext bearbeiten]Wendet man ein lineares Mehrschrittverfahren auf die Testgleichung an, ergibt sich wieder mit die Gleichung
Dies ist eine lineare Differenzengleichung, die man einfach lösen kann. Denn die Folge ist eine nichttriviale Lösung dieser Differenzengleichung, wenn u eine Nullstelle des charakteristischen Polynoms
ist, wobei man die Polynome
eingeführt hat. Also bekommt man mit den von abhängenden Nullstellen des Polynoms die Lösungen zur Testgleichung und daher liegt im Stabilitätsgebiet des Verfahrens, wenn alle diese Lösungen gegen 0 gehen für . Daher kann man die betragsmaximale Nullstelle als Stabilitätsfunktion des Verfahrens ansehen.
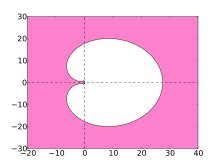
Diese Interpretation erscheint sehr unhandlich. Allerdings interessiert man sich oft weniger für die Stabilitätsfunktion, sondern für das Stabilitätsgebiet . Der Rand dieses Gebietes besteht aus denjenigen , bei dem für die Nullstellen gilt, wo die Nullstellen also auf dem komplexen Einheitskreis liegen. Da gilt, ist die Bestimmung des Stabilitätsgebiets bei Mehrschrittverfahren sogar besonders einfach, denn seinen Rand erhält man i. W. explizit durch
Als Beispiel wird das Stabilitätsgebiet für das 6-stufige BDF-Verfahren gezeigt.
Die Stabilitätsfunktion von allgemeinen linearen Verfahren
[Bearbeiten | Quelltext bearbeiten]Obwohl auch Mehrschrittverfahren in der Gestalt von allgemeinen linearen Verfahren geschrieben werden können, ist die Struktur ähnlich derjenigen der Runge-Kutta-Verfahren weiter oben. Daher bekommt man ein ähnliches Ergebnis. Für den Vektor der Stufenlösungen gilt
und der Zeitschritt wird daher zu
In jedem Zeitschritt erfolgt also die Multiplikation mit derselben Matrix
Es gilt daher , wenn die Potenzen von gegen 0 gehen, also alle Eigenwerte von innerhalb des komplexen Einheitskreises liegen. Daher kann man hier den Spektralradius von als Stabilitätsfunktion in der Definition des Stabilitätsgebiets ansehen.
Weitergehende Bedeutung für lineare Systeme
[Bearbeiten | Quelltext bearbeiten]Die obige Testgleichung von Dahlquist ist sehr einfach, hat aber eine weitergehende Bedeutung für Systeme von linearen, autonomen und homogenen Differentialgleichungen
Die exakte Lösung ist mit dem Matrixexponential . Die numerische Lösung kann man jetzt mit der Matrix-Stabilitätsfunktion darstellen. Wenn dabei die Jordan-Normalform von ist, gilt
Bei einer diagonalisierbaren Matrix ist, ist eine Diagonalmatrix mit den Diagonalelementen . Wenn für alle Eigenwerte von gilt, dass ist, dann konvergiert auch hier . Bei dieser Differentialgleichung sieht man gleichzeitig, dass es sinnvoll ist, als offene Menge zu definieren. Denn im diagonalisierbaren Fall bleiben zwar Lösungen auf dem Rand mit noch beschränkt, aber im Allgemeinen nicht mehr, wenn mehrfache Eigenwerte mit Jordanblöcken auftreten.
Literatur
[Bearbeiten | Quelltext bearbeiten]- E. Hairer, G. Wanner: Solving Ordinary Differential Equations II, Stiff problems. Springer Verlag.
- K. Strehmel, R. Weiner, H. Podhaisky: Numerik gewöhnlicher Differentialgleichungen – Nichtsteife, steife und differential-algebraische Gleichungen. Springer Spektrum, 2012.


























































![{\displaystyle Y=zAY+Uy^{[n-1]}\quad \Rightarrow Y=(I-zA)^{-1}Uy^{[n-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42c652d7fab80eea9bdb550278be9fcdf94b6ef)
![{\displaystyle y^{[n]}=zBY+Vy^{[n-1]}=(V+zB(I-zA)^{-1}U{\big )}y^{[n-1]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2103de9fe45c2b1a5531849e52f2b3d046ca4c8b)

![{\displaystyle y^{[n]}=M(z)^{n}y^{[0]}\to 0\,(n\to \infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e44afdd17b14531c597ce322a00d6d310c72b666)














