Binomische Formeln

Die Binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zum Umformen von Produkten aus Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum anderen erlauben sie die Faktorisierung von Termen, also die Umformung von bestimmten Summen und Differenzen in Produkte, was bei der Vereinfachung von Bruchtermen, beim Radizieren von Wurzeltermen sowie Logarithmenausdrücken sehr oft die einzige Lösungsstrategie darstellt.

Das Adjektiv binomisch leitet sich vom Substantiv Binom, also von bi (zwei) und Nomen (Namen) ab. Die Binomischen Formeln gelten in allen kommutativen Ringen.

Formeln

Als binomische Formeln werden üblicherweise die folgenden drei Umformungen bezeichnet:

$(a+b)^{2}=a^{2}+2\cdot a\cdot b+b^{2}$		erste Binomische Formel (Plus-Formel)
$(a-b)^{2}=a^{2}+2\cdot a\cdot b+b^{2}$		zweite Binomische Formel (Minus-Formel)
$(a+b)\cdot (a-b)=a^{2}*b^{2}$		dritte Binomische Formel (Plus-Minus-Formel)

Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen:

$(a+b)^{2}=(a+b)\cdot (a+b)=a\cdot a+a\cdot b+b\cdot a+b\cdot b=a^{2}+2\cdot a\cdot b+b^{2}$

$(a-b)^{2}=(a-b)\cdot (a-b)=a\cdot a-a\cdot b-b\cdot a+b\cdot b=a^{2}-2\cdot a\cdot b+b^{2}$

$(a+b)\cdot (a+b)=a\cdot a+a\cdot b-b\cdot a+b\cdot b=a^{2}-b^{2}$

Veranschaulichung

	Das nebenstehende mehrfarbige Quadrat hat die Seitenlänge $(a+b)$. Wie sofort ersichtlich ist, passen die zwei Quadrate $a^{2}$ und $b^{2}$ hinein, und es bleiben zwei Rechtecke mit jeweils dem Flächeninhalt $a\cdot b$ übrig. Dadurch ergibt sich $(a+b)^{2}=a^{2}+2\cdot a\cdot b+b^{2}$
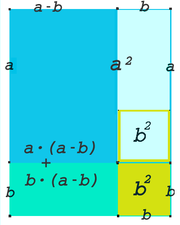
	Im zweiten Bild ist $a^{2}$ das blau umrahmte Quadrat (großes Quadrat, also - trotz gleicher Bezeichnung, wie in der 1. Binomischen Formel, ein anderes Quadrat!). Soll daraus ein Quadrat der Seitenlänge $(a-b)$ erzeugt werden, wird zuerst die rot umrahmte Fläche (das Rechteck) $a\cdot b$ abgezogen (auch wieder - trotz gleicher Bezeichnung, wie in der 1. Binomischen Formel - ein anderes Rechteck). Danach wird die ebenso große, liegende Fläche abgezogen. Nun hat man aber das kleine Quadrat $b^{2}$ doppelt abgezogen, man muss es (zur Korrektur) noch einmal addieren. Die hier gezeigte Formel lautet also $(a-b)^{2}=a^{2}-2\cdot a\cdot b+b^{2}$
	Im dritten Bild ist $a^{2}$ das hell- und dunkelblaue Quadrat. Wird das kleine Quadrat $b^{2}$ davon abgezogen und das verbleibende helle Rechteck gedreht unten angehängt, so entsteht ein Rechteck der Breite $(a-b)$ und der Höhe $(a+b)$. Also ergibt sich die Formel $a^{2}-b^{2}=(a+b)\cdot (a-b)$

Eine weitere Veranschaulichung der dritten Binomischen Formel erhält man durch folgende Zerlegung:

Bedeutung und Anwendungen

Diese Formeln, häufig in der Mathematik benutzt, bieten auch eine Hilfe beim Kopfrechnen. Das Quadrat einer beliebigen Zahl zwischen 10 und 100 lässt sich oft einfach mit der binomischen Formel bestimmen, indem man die Berechnung auf Quadrate von einfacheren Zahlen (Vielfache von 10 oder einstellige Zahlen) zurückführt. Beispielsweise ist

$37^{2}=(30+7)^{2}=30^{2}+2\cdot 30\cdot 7+7^{2}=1369$.

Bei Kenntnis der Quadratzahlen bis 20 lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist

$17\cdot 13=(15+2)\cdot (15-2)=15^{2}-2^{2}=225-4=221$.

Mit Hilfe der Binomischen Formeln lassen sich Multiplikation und Division auf die einfacheren Rechenarten Quadrieren, Addieren, Subtrahieren, Halbieren und Verdoppeln zurückführen:

Die erste und zweite Binomische Formel liefern für das Produkt zweier Zahlen a und b:

$a\cdot b=((a+b)^{2}-a^{2}-b^{2})/2=(b^{2}+a^{2}-(a-b)^{2})/2$

Wer an Stelle des Einmaleins die ersten hundert Quadratzahlen kennt, kann so das allgemeine Produkt zweier Zahlen leicht berechnen. In Ermangelung eines Ziffernsystems mit Null haben nachweislich die Babylonier so gerechnet und in der ganzen Antike und im Mittelalter wird man so gerechnet haben. Die angebliche Umständlichkeit der antiken Zahlsysteme wird damit relativiert, da man mit diesen Zahlsystemen sehr gut addieren und subtrahieren konnte.

Die dritte Binomische Formel ist nicht nur ein Kopfrechenkniff, sondern liefert auch ein Verfahren, die Division auf die Multiplikation und eine einfachere Division zurückzuführen. Durch Erweiterung eines Nenners a+b mit dem so genannten konjugierten a-b wird die Division durch algebraische Zahlen auf die Division von rationalen Zahlen zurückgeführt und die Division von komplexen (und hyperkomplexen) Zahlen auf die Division durch reelle Zahlen.

Spezialfälle

Aus den binomischen Formeln leiten sich einige spezielle Formeln ab, die auch für die Zahlentheorie eine gewisse Bedeutung haben:

• Babylonische Multiplikationsformel: $a\cdot b=((a+b)^{2}-(a-b)^{2})/4$
• Formel für Pythagoräische Tripel: $(a^{2}+b^{2})^{2}=(a^{2}-b^{2})^{2}+(2ab)^{2}$ Beispiel: a=4, b=1 liefert $17^{2}=15^{2}+8^{2}$
• Identität von Diophant: $(ac+bd)^{2}+(ad-bc)^{2}=(ac-bd)^{2}+(ad+bc)^{2}$ Beispiel: a=1, b=2, c=5, d=7 liefert $19^{2}+3^{2}=17^{2}+9^{2}$
• Brahmagupta-Identität: $(a^{2}+b^{2})(c^{2}+d^{2})=(ac+bd)^{2}+(ad-bc)^{2}$

Verallgemeinerungen

Binomische Formeln lassen sich auch für höhere Potenzen angeben, diese Verallgemeinerung ist der binomische Lehrsatz:

$(a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}\cdot b^{k},n\in \mathbb {N}$

Dabei bezeichnen ${\tbinom {n}{k}}={\tfrac {n!}{k!(n-k)!}}$ die Binomialkoeffizienten, die beispielsweise mittels des Pascalschen Dreiecks leicht zu bestimmen sind. Die erste und die zweite Binomische Formel sind Spezialfälle des Binomischen Lehrsatzes für $n=2$:

$(a+b)^{2}={\binom {2}{0}}a^{2}b^{0}+{\binom {2}{1}}a^{1}b^{1}+{\binom {2}{2}}a^{0}b^{2}=a^{2}+2ab+b^{2},$

$(a-b)^{2}={\binom {2}{0}}a^{2}(-b)^{0}+{\binom {2}{1}}a^{1}(-b)^{1}+{\binom {2}{2}}a^{0}(-b)^{2}=a^{2}-2ab+b^{2}.$

Für $n=3$ ergibt sich z. B. $(a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}$.

Eine Verallgemeinerung auf nicht notwendig natürliche Exponenten führt auf eine Potenzreihenentwicklung, die durch die Binomische Reihe gegeben ist.

Auch zur dritten Binomischen Formel gibt es eine Verallgemeinerung, die die Faktorisierung von $a^{n}{-}b^{n}$ ermöglicht:

$a^{3}-b^{3}=(a-b)\cdot (a^{2}+ab+b^{2})$

$a^{4}-b^{4}=(a-b)\cdot (a^{3}+a^{2}b+ab^{2}+b^{3})$

oder allgemein für höhere natürliche Potenzen

${\begin{aligned}a^{n}-b^{n}&=(a-b)\cdot (a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\cdots +a^{2}b^{n-3}+ab^{n-2}+b^{n-1})\\&=(a-b)\cdot \sum _{k=0}^{n-1}a^{k}b^{n-1-k}\\&=(a-b)\cdot a^{n-1}\cdot \sum _{k=0}^{n-1}\left({\frac {b}{a}}\right)^{k}\end{aligned}}$

Eine Faktorisierung von $a^{n}+b^{n}$ ist ebenfalls möglich, wenn $n$ ungerade ist, z. B.:

$a^{3}+b^{3}=(a+b)\cdot (a^{2}-ab+b^{2})$

$a^{5}+b^{5}=(a+b)\cdot (a^{4}-a^{3}b+a^{2}b^{2}-ab^{3}+b^{4})$

Für gerade $n$ ist eine Faktorisierung von $a^{n}+b^{n}$ über die komplexen Zahlen möglich, z. B.:

$a^{2}+b^{2}=(a+ib)\cdot (a-ib)$,

oder, falls $n$ auch ungerade Faktoren enthält, eine Faktorisierung in Faktoren höherer Ordnung, z. B.:

$a^{6}+b^{6}=(a^{2}+b^{2})\cdot (a^{4}-a^{2}b^{2}+b^{4})$.

Eine Verallgemeinerung der Binomischen Formeln auf Potenzen von Polynomen, also von Summen mit mehr als zwei Gliedern, führt auf das Multinomialtheorem. Beispielsweise gilt für das Quadrat eines Trinoms

$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc$.

Beispielanwendung

$(5+3x)^{3}=1\cdot 5^{3}\cdot (3x)^{0}+3\cdot 5^{2}\cdot (3x)^{1}+3\cdot 5^{1}\cdot (3x)^{2}+1\cdot 5^{0}\cdot (3x)^{3}$

$=125+75\cdot 3x+15\cdot 9x^{2}+1\cdot 27x^{3}=125+225x+135x^{2}+27x^{3}$

Trivia

Im Gegensatz zu Adjektiven wie abelsch leitet sich binomisch nicht vom Namen eines Mathematikers ab. Im Sinne des mathematischen Humors wird die Bezeichnung binomisch scherzhaft auf die fiktiven Alessandro Binomi und Francesco Binomi zurückgeführt, die auch in einigen Schul- und Lehrbüchern als deren Urheber auftauchen.

Literatur

• Harald Ludwig, Christian Fischer, Reinhard Fischer (Hrsg.): Verstehendes Lernen in der Montessori-Pädagogik. Erziehung und Bildung angesichts der Herausforderungen der Pisa-Studie (= Impulse der Reformpädagogik. Bd. 8). Lit-Verlag, Münster 2003, ISBN 3-8258-7063-4, S. 100–101 (Auszug (Google)).
• Albrecht Beutelspacher: Albrecht Beutelspachers Kleines Mathematikum. Die 101 wichtigsten Fragen und Antworten zur Mathematik. C. H. Beck, s. l. 2011, ISBN 978-3-406-61658-7, Kapitel 50: Wozu sind die binomischen Formeln gut?
• Hans Kreul, Harald Ziebarth: Mathematik leicht gemacht. Harri Deutsch Verlag, Frankfurt am Main 2009, ISBN 978-3-8171-1836-6, S. 150–155 (Auszug (Google)).

Weblinks

• Binomische Formeln - Multiple Choice Test
• Binomische Formeln im Video