Kusszahl

In der Geometrie ist die $n$-te Kusszahl (auch Kontaktzahl) die maximale Anzahl an $n$-dimensionalen Einheitskugeln (Kugeln mit Radius 1), die gleichzeitig eine weitere solche Einheitskugel im euklidischen Raum berühren können, ohne dass Überschneidungen auftreten. Von Gitterkusszahlen spricht man, wenn die Mittelpunkte der Kugeln in einem Gitter angeordnet sind. Als Kusszahlenproblem ist das Fehlen einer allgemeinen Formel zur Berechnung der Kusszahlen bekannt.

Kusszahlen in verschiedenen Dimensionen

Die erste Kusszahl ist 2.

Die zweite Kusszahl ist 6.

n = 1:  In einer Dimension ist die Einheitskugel keine Kugel, sondern eine Strecke, deren Endpunkte den Abstand 1 vom Ursprung haben. Hier kann an beide Endpunkte jeweils eine weitere Strecke angefügt werden, sodass die Kusszahl für eine Dimension offensichtlich 2 ist.

n = 2:  In der zweiten Dimension ist die Einheitskugel keine Kugel, sondern ein Kreis mit Radius 1. Anschaulich entspricht damit das Problem der Ermittlung der Kusszahl in dieser Dimension der Aufgabe, möglichst viele Münzen so anzuordnen, dass sie alle eine gleich große zentrale Münze berühren. Es ist leicht zu sehen (und zu beweisen), dass die Kusszahl für die zweite Dimension 6 ist.

n = 3:  In der dritten Dimension ist die Ermittlung der Kusszahl nicht so einfach; vgl. die Graphik rechts. Es ist leicht, zwölf Kugeln so anzuordnen, dass sie die zentrale Kugel berühren (beispielsweise so, dass ihre Mittelpunkte die Ecken eines Kuboktaeders bilden). Man erkennt aber noch viel Leerraum zwischen den Kugeln und fragt sich, ob eine dreizehnte Kugel hinzugefügt werden kann. Dieses Problem war Thema eines berühmten Streites zwischen Isaac Newton und dem Mathematiker David Gregory, den diese 1692 über die Keplerschen Vermutung führten. Newton behauptete, das Maximum sei zwölf, Gregory meinte, es sei dreizehn. Im 19. Jahrhundert erschienen die ersten Veröffentlichungen, die behaupteten, den Beweis für Newtons Behauptung zu enthalten. Nach heutigen Standards wurden formelle Beweise jedoch erst 1953 von Kurt Schütte und Bartel Leendert van der Waerden und 1956 von John Leech erbracht.

n = 4:  Erst Anfang des 21. Jahrhunderts wurde bewiesen, dass die Kusszahl für die vierte Dimension 24 ist.

n > 4:  Ferner sind die Kusszahlen für die Dimensionen  n = 8  (240) und  n = 24  (196.560) bekannt; im 24-dimensionalen Raum werden die Kugeln auf den Punkten des Leech-Gitters platziert, sodass kein Platz übrig ist. Die exakten Kusszahlen für die Dimensionen 8 und 24 wurden 1979 unabhängig voneinander von Andrew M. Odlyzko und Neil J. A. Sloane bzw. Vladimir Levenshtein ermittelt.

Die folgende Tabelle gibt die bekannten Grenzen für die Kusszahl bis zur Dimension 24 wieder.

Die dritte Kusszahl ist 12.
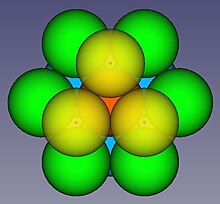
Die mittige Kugel (rot) wird von
6 Kugeln (grün) in gleicher Ebene,
3 Kugeln (gelb) darüber und
3 Kugeln (blau, 60° gegen gelbe verdreht) darunter berührt.

Das exponentielle Wachstum der Kusszahlen; Dimensionen 1 bis 24. Die graue Fläche ist durch die oberen und unteren Grenzen (s. Tabelle) begrenzt.

Kusszahlen in den Dimensionen 1…24

Dimen- sion	Kusszahl			Dimen- sion	Kusszahl
	untere Grenze	obere Grenze			untere Grenze	obere Grenze
1	2			13	1154	2069
2	6			14	1606	3183
3	12			15	2564	4866
4	24			16	4320	7355
5	40	44		17	5346	11.072
6	72	78		18	7398	16.572
7	126	134		19	10.688	24.812
8	240			20	17.400	36.764
9	306	364		21	27.720	54.584
10	500	554		22	49.896	82.340
11	582	870		23	93.150	124.416
12	840	1.357		24	196.560

Schätzungen zeigen, dass das Wachstum der Kusszahlen exponentiell ist; vgl. Graphik neben der Tabelle. Die Basis des exponentiellen Wachstums ist unbekannt.

Über die Kusszahlen in noch höheren Dimensionen ist eher wenig bekannt; untere Schranken sind etwa für die Dimensionen  n = 32  (276.032),  n = 36  (438.872),  n = 40  (991.792),  n = 44  (2.948.552),  n = 64  (331.737.984) und  n = 80  (1.368.532.064) bekannt.

Gitterkusszahlen in verschiedenen Dimensionen

Die exakten Gitterkusszahlen sind für die Dimensionen 1 bis 9 und 24 bekannt.
Die folgende Tabelle gibt die Gitterkusszahlen bzw. die bekannten unteren Grenzen bis zur Dimension 24 wieder:

Gitterkusszahlen in den Dimensionen 1..24

Dimension	Gitterkusszahl		Dimension	Gitterkusszahl
1	2		13	≥ 918
2	6		14	≥ 1422
3	12		15	≥ 2340
4	24		16	≥ 4320
5	40		17	≥ 5346
6	72		18	≥ 7398
7	126		19	≥ 10.668
8	240		20	≥ 17.400
9	272		21	≥ 27.720
10	≥ 336		22	≥ 49.896
11	≥ 438		23	≥ 93.150
12 ⁠	≥ 756		24 ⁠	196.560

Die Gitterpackungen für die Dimensionen 12 und 24 haben eigene Namen:

 

Coxeter-Todd-Gitter (nach Harold Scott MacDonald Coxeter und John Arthur Todd)

 

Leech-Gitter (nach John Leech)

Berechnung

Werden die Kugelradien auf $1/2$ normiert und der Ursprung des Koordinatensystems in den Mittelpunkt der zentralen Kugel gelegt, dann muss bei $N$ küssenden Kugeln das folgende System von Ungleichungen erfüllt sein:

$\exists$ $x{\Big (}$$\forall$ $n:||x_{n}||=1\land \forall n\neq m:||x_{n}-x_{m}||\geq 1{\Big )}$

Dabei laufen $m$ und $n$ von $1$ bis $N$ und $x=(x_{n})_{n\in \{1\dots {N}\}}$ ist die Sequenz der Vektoren zu den $N$ Kugelmittelpunkten, $||a||$ ist die Norm (Länge) des Vektors $a$. Aus Symmetriegründen reicht es, wenn der zweite Allquantor sich über alle $m$, $n$ mit $m<n$ erstreckt.
In einem $D$-dimensionalen reellen Vektorraum $\mathbb {R} ^{D}$ wird daraus nach Übergang zu den Normquadraten in Matrixschreibweise

$\exists x{\Big (}\forall n:{x_{n}}^{T}x_{n}=1\land \forall m<n:(x_{n}-x_{m})^{T}(x_{n}-x_{m})\geq 1{\Big )}$ .

Dabei sind die Vektoren $x$ als Spaltenvektoren aufgefasst, und $x^{T}$ ist der entsprechende Zeilenvektor (Transponierte Matrix), $a^{T}\!b$ das Skalarprodukt. Dieses System von Ungleichungen geht nach Umformung und Einführung von Hilfsvariablen $y_{mn}$ über in das Gleichungssystem

$\exists x,y:\sum _{n=1}^{N}({x_{n}}^{T}x_{n}-1)^{2}+\sum _{\begin{smallmatrix}(m,n)\in {N}\times {N}\\m<n\end{smallmatrix}}{\big (}(x_{n}-x_{m})^{T}(x_{n}-x_{m})-1-{y_{mn}}^{2}{\big )}^{2}=0$.

Das obige Gleichungssystem hat insgesamt $D\!\cdot \!{N}$ Gleichungen für die $N$ Vektoren $x$, dazu kommen die Hälfte von $N\!\cdot \!(N\!-\!1)$ für die Matrix $y$; insgesamt also $D\!\cdot \!{N}+N\!\cdot \!(N\!-\!1)/2$ Gleichungen. Wegen der relativen Größe der zu testenden Zahl $N$ der küssenden Kugeln stößt man schnell an die praktischen Grenzen der Berechenbarkeit.

Abschätzungen
Die allgemeine Form der unteren Grenze für $n$-dimensionale Gitterkennzahlen ist gegeben durch

$\eta \geq {\frac {\zeta (n)}{2^{n-1}}}$ ,

wobei $\zeta$ die Riemannsche Zeta-Funktion ist. Diese Grenze wird durch den Satz von Minkowski-Hlawka (nach Hermann Minkowski und Edmund Hlawka) spezifiziert.

Siehe auch

• dichteste Kugelpackung

Literatur

• Florian Pfender, Günter M. Ziegler: Kissing Numbers, Sphere Packings, and Some Unexpected Proofs. Notices of the American Mathematical Society, S. 873–883. (PDF)
• Eric W. Weisstein: Kissing Number. In: MathWorld (englisch).
• Christine Bachoc, Frank Vallentin: New upper bounds for kissing numbers from semidefinite programming. In: Journal of the American Mathematical Society. Band 21, 2008, S. 909–924. arxiv:math.MG/0608426
• John Horton Conway, Neil James Alexander Sloane, Eiichi Bannai: Sphere packings, lattices, and groups. Springer, 1999. ISBN 978-0-387-98585-5. eingeschränkte Online-Version (Google books)
• Casselman zum Kissing Number Problem und seiner Geschichte, Notices of the AMS, 2004, Heft 8, PDF-Datei

Weblinks

Commons: Kusszahl – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Kusszahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen