Rücktransport
In verschiedenen Teilgebieten der Mathematik bezeichnet man als Rücktransport[1] oder Pullback (auch: Zurückziehung, Rückzug) Konstruktionen, die ausgehend von einer Abbildung und einem Objekt , das in irgendeiner Weise zu gehört, ein entsprechendes, „entlang von zurückgezogenes“ Objekt für liefern; es wird häufig mit bezeichnet.
Das duale Konzept heißt meist Pushforward.
In der Kategorientheorie ist Pullback eine andere Bezeichnung für das Faserprodukt. Das duale Konzept wird hier Pushout, cokartesisches Quadrat oder Fasersumme genannt.
Motivation: Der Rücktransport einer glatten Funktion[Bearbeiten | Quelltext bearbeiten]
Sei ein Diffeomorphismus zwischen glatten Mannigfaltigkeiten und sei eine glatte Funktion auf . Dann ist der Rücktransport von bezüglich definiert durch
- mit
Der Rücktransport ist also eine glatte Funktion .
Schränkt man die Funktion auf eine offene Teilmenge ein, so erhält man ebenso eine glatte Funktion auf . Der Rücktransport ist also ein Morphismus zwischen den Garben der glatten Funktionen von und .
Der Rücktransport eines Vektorbündels[Bearbeiten | Quelltext bearbeiten]
Seien und topologische Räume, ein Vektorbündel über und eine stetige Abbildung. Dann ist das zurückgezogene Vektorbündel definiert durch
zusammen mit der Projektion .[2]
Es kann nun gezeigt werden, dass es einen Vektorbündelhomomorphismus gibt, so dass das Diagramm
kommutiert.[2] Somit ist das zurückgezogene Vektorbündel ein Spezialfall eines Faserproduktes. Für einen fixierten Punkt ist eine lineare Abbildung zwischen Vektorräumen, daher gibt es eine duale Abbildung . In diesem Kontext wird das zurückgezogene Vektorbündel auch mittels notiert und man nennt es auch Pullbackbündel von bezüglich .
Zurückgezogene Schnitte in Vektorbündeln[Bearbeiten | Quelltext bearbeiten]
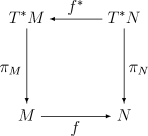
Im Bereich der Differentialgeometrie werden meist glatte Mannigfaltigkeiten anstatt beliebiger topologischer Räume und betrachtet. Dann wird auch zusätzlich gefordert, dass die Abbildung und das Vektorbündel differenzierbar sind. Betrachtet man die entsprechenden Tangentialräume anstatt beliebiger Vektorbündel, so ist die Abbildung der Pushforward von und die zurückziehende Abbildung ist die duale Abbildung.[3]
Ist ein Schnitt im Vektorbündel , so ist der zurückgezogene Schnitt, der durch
für alle gegeben ist.
Rücktransport bestimmter Schnitte in Vektorbündeln[Bearbeiten | Quelltext bearbeiten]
Im vorigen Abschnitt wurde der Rücktransport eines Schnitts in einem Vektorbündel definiert. In diesem Abschnitte werden konkrete Instanzen solcher Rücktransporte von Schnitten aufgeführt. Dazu sind in diesem Abschnitt und glatte Mannigfaltigkeiten und eine glatte Abbildung.
Glatte Funktionen[Bearbeiten | Quelltext bearbeiten]
Die Menge der glatten Funktionen kann auf natürliche Weise mit dem Vektorraum der glatten Schnitte im Vektorbündel identifiziert werden.[4] Entsprechend kann der Rücktransport einer glatten Funktion auch als Rücktransport eines glatten Schnittes des Vektorbündels aufgefasst werden.
1-Formen[Bearbeiten | Quelltext bearbeiten]
Der Pushforward von entspricht gerade der äußeren Ableitung von , was ein Vektorbündelhomomorphismus vom Tangentialraum in den Tangentialraum ist. Der duale Operator ist somit ein Bündelhomomorphismus vom Kotangentialbündel in das Kotangentialbündel .
Sei ein glatter Schnitt in , was per Definition eine 1-Form ist. Dann gilt für den Rücktransport von
für ein .[3]
Differentialformen[Bearbeiten | Quelltext bearbeiten]
Da die Menge der Differentialformen ein Vektorbündel bildet, kann man den Rücktransport einer Differentialform untersuchen.
Ist eine differenzierbare Abbildung und eine k-Form auf , so gilt für die auf zurückgezogene Differentialform die Gleichung
für Tangentialvektoren im Punkt gegeben.[5]
Literatur[Bearbeiten | Quelltext bearbeiten]
- R. Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences 75). 2. Auflage. Springer, New York NY u. a. 1988, ISBN 0-387-96790-7.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Otto Forster: Riemannsche Flächen (= Heidelberger Taschenbücher 184). Springer, Berlin u. a. 1977, ISBN 3-540-08034-1. S. 62 (Englisch: Lectures on Riemann Surfaces (= Graduate Texts in Mathematics 81). Corrected 2nd printing. ebenda 1991, ISBN 3-540-90617-7).
- ↑ a b Allen Hatcher: Vector Bundles & K-Theory. Version 2.1, May 2009, S. 18 online (PDF; 1,11 MB).
- ↑ a b John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 136.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 111.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 303.















































