Tangentialraum
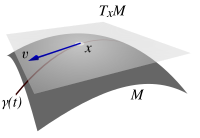
In der Differentialgeometrie ist ein Tangentialraum (auch Tangentenraum genannt) ein Vektorraum, der eine differenzierbare Mannigfaltigkeit am Punkt linear approximiert. Sei eine differenzierbare Kurve mit und dem Kurvenparameter , dann ist:
ein Tangentialvektor. Die Tangentialvektoren in einem Punkt spannen einen Vektorraum auf, den Tangentialraum . Siehe auch Tangentialbündel.
In der algebraischen Geometrie muss man diesen Definitionsansatz modifizieren, um singuläre Punkte und wechselnde Dimensionen zu berücksichtigen.
Dieser Artikel befasst sich nur mit dem Tangentialraum über einer differenzierbaren Mannigfaltigkeit im Sinne der Differentialgeometrie.
Übersicht[Bearbeiten | Quelltext bearbeiten]
Am einfachsten ist eine differenzierbare Mannigfaltigkeit zu veranschaulichen, die als Untermannigfaltigkeit in einen Euklidischen Raum (z. B. den ) eingebettet ist. Als Beispiel soll die Sphäre (= Kugeloberfläche) im dienen. Der Tangentialraum in einem Punkt ist dann die Ebene durch den Nullpunkt, die parallel zur Tangentialebene an die Kugel im Punkt ist.
Ein Vektorfeld ordnet jedem Punkt einer Mannigfaltigkeit einen Vektor aus dem zugehörigen Tangentialraum zu. Zum Beispiel könnte man mit einem Vektorfeld die Windstärke und -richtung auf der Erdoberfläche angeben.
Alle Tangentialräume einer Mannigfaltigkeit werden als Tangentialbündel von zusammengefasst; das Tangentialbündel ist selbst eine Mannigfaltigkeit; seine Dimension ist doppelt so groß wie die von .
Formale Definitionen[Bearbeiten | Quelltext bearbeiten]
In der Literatur ist es üblich, gleich drei verschiedene Definitionen anzugeben, die einer geometrischen, einer algebraischen und einer theoretisch-physikalischen (auf Tensoren hinarbeitenden) Sichtweise entsprechen. Der anschauliche geometrische Zugang erweist sich in der Anwendung jedoch als der am mühsamsten zu handhabende.
Die beiden auf die geometrische Definition folgenden algebraischen Definitionen des Tangentialraums funktionieren allerdings nur für Mannigfaltigkeiten der Klasse , aber nicht für mit .
Geometrische Definition: Richtungsfelder von Kurven[Bearbeiten | Quelltext bearbeiten]
Gegeben seien eine -dimensionale -Mannigfaltigkeit mit , ein Punkt aus , eine offene Umgebung von und eine Karte .
Ist mit eine differenzierbare Kurve in , so ist eine differenzierbare Kurve im . Die Ableitung existiert also. Diese Ableitung ist ein Vektor im . Kurven , für die übereinstimmt, bilden eine Äquivalenzklasse. Eine solche Äquivalenzklasse nennt man einen Tangentialvektor von in und schreibt dafür . Der Tangentialraum ist die Menge aller dieser Tangentialvektoren; man kann zeigen, dass er nicht von der Wahl der Karte abhängt.
Es bleibt zu zeigen, dass durch Erklärung von Vektoraddition und Skalarmultiplikation zu einem Vektorraum wird. Dazu definiert man die Abbildung durch , wobei die Funktion auf der rechten Seite ein beliebiger Repräsentant der Äquivalenzklasse ist. Man zeigt nun, dass diese Abbildung bijektiv ist und überträgt mit ihrer Hilfe die Vektorraumoperationen von nach ; man zeigt außerdem, dass diese Konstruktion von der Wahl der Karte unabhängig ist.
Erste algebraische Definition: verallgemeinerte Ableitungen[Bearbeiten | Quelltext bearbeiten]
Sei eine -Mannigfaltigkeit. Eine Funktion gehört zur Klasse , falls für jede Karte unendlich oft differenzierbar ist. Das so definierte ist eine assoziative Algebra.
Fixieren wir einen Punkt in . Eine Derivation an ist eine lineare Abbildung , die für alle und in die (analog zur Produktregel) folgende Eigenschaft hat: . Diese Derivationen bilden auf natürliche Weise einen reellen Vektorraum; dies ist der Tangentialraum .
Die Beziehung zwischen den zuvor definierten Tangentialvektoren und den Derivationen ist wie folgt: falls eine Kurve mit Tangentialvektor ist, dann ist die entsprechende Derivation (mit der Ableitung im üblichen Sinne, da eine Funktion von nach ist).
Zweite algebraische Definition: Dualraum von I/I²[Bearbeiten | Quelltext bearbeiten]
Sei wieder eine -Mannigfaltigkeit und ein Punkt in . Betrachten wir nun das Ideal von , das aus allen glatten Funktionen besteht, die auf abbilden. Dann sind und reelle Vektorräume, und wird als der Dualraum des Quotientenraums definiert. wird auch als Kotangentialraum bezeichnet (siehe unten).
Während diese Definition die abstrakteste ist, ist sie auch diejenige, die man am leichtesten auf andere Situationen übertragen kann, beispielsweise auf Varietäten, wie sie in der algebraischen Geometrie betrachtet werden.
Sei eine Derivation an . Dann ist für jedes in (denn es existieren mit , somit ), womit eine lineare Abbildung induziert. Umgekehrt ist eine Derivation, wenn eine lineare Abbildung ist. Dies zeigt, dass sich der über Derivationen und der über definierte Tangentialraum entsprechen.
Tangentialraum in der algebraischen Geometrie[Bearbeiten | Quelltext bearbeiten]
Die beiden algebraischen Definitionen funktionieren genauso auch für algebraische Varietäten, wobei hier der Tangentialraum auch als Zariski-Tangentialraum bezeichnet wird. Im Unterschied zu Mannigfaltigkeiten können algebraische Varietäten aber Singularitäten haben, dort hat dann der Tangentialraum eine höhere Dimension als in glatten Punkten.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Wenn eine offene Teilmenge des ist, so kann man in natürlicher Weise als eine -Mannigfaltigkeit betrachten. Alle Karten sind hierbei die Identität, und die Tangentialräume werden mit dem identifiziert.
Tangentialvektoren als Richtungsableitungen[Bearbeiten | Quelltext bearbeiten]
Eine Sichtweise von Tangentialvektoren ist, sie als Richtungsableitungen zu sehen. Für einen Vektor im definiert man die Richtungsableitung einer glatten Funktion an einem Punkt durch
Diese Abbildung ist offenbar eine Derivation. Tatsächlich ist sogar jede Derivation von () von dieser Form. So existiert eine Bijektion zwischen Vektoren (als Tangentialvektor am Punkt gedacht) und den Derivationen.
Da Tangentialvektoren an einer allgemeinen Mannigfaltigkeit als Derivationen definiert werden können, ist es nur natürlich, sie auch als Richtungsableitungen zu sehen. Konkret kann man für einen Tangentialvektor von an einem Punkt (als Derivation gesehen) die Richtungsableitung in Richtung für Element von wie folgt definieren:
Sehen wir im Sinne der geometrischen Definition des Tangentialraums als für eine Kurve , schreiben wir
- .
Die Totalableitung einer Abbildung[Bearbeiten | Quelltext bearbeiten]
Jede differenzierbare Abbildung zwischen zwei differenzierbaren Mannigfaltigkeiten induziert eine lineare Abbildung
zwischen den entsprechenden Tangentialräumen, definiert durch
für die geometrische Definition des Tangentialraums und
für die Definition mittels Derivationen.
Die lineare Abbildung wird mit Differential, Ableitung, Totalableitung oder auch Tangentialabbildung bezeichnet. Auch hier variieren die Notationen stark. Benutzt werden vor allem: , , und .
In einem gewissen Sinne ist die Totalableitung die beste lineare Approximation von in einer Umgebung von . In lokalen Koordinaten kann man die Totalableitung als Jacobische Matrix darstellen.
Ist die Tangentialabbildung surjektiv, hat also die Jacobi-Matrix überall vollen Rang, so nennt man die zugrundeliegende Funktion Submersion; ist die Tangentialabbildung injektiv, Immersion.
Ein wichtiges Resultat bezüglich Tangentialabbildungen ist der Satz:
- Genau dann, wenn ein lokaler Diffeomorphismus bei in ist, ist ein linearer Isomorphismus.
Dies ist eine Verallgemeinerung des Satzes über inverse Funktionen auf Abbildungen zwischen Mannigfaltigkeiten.
Richtungen der Tangentialvektoren[Bearbeiten | Quelltext bearbeiten]
Falls eine glatte Mannigfaltigkeit mit Rand ist und , dann können die Vektoren im Tangentialraum in drei Klassen aufgeteilt werden:
- heißt nach innen gerichtet für ein , wenn eine glatte Kurve existiert mit und .
- heißt nach aussen gerichtet für ein , wenn eine glatte Kurve existiert mit und .
- die Restlichen sind tangent zum Rand.[1]
Kotangentialraum[Bearbeiten | Quelltext bearbeiten]
Da der Tangentialraum am Punkt der Mannigfaltigkeit die Struktur eines Vektorraums trägt, kann man den Dualraum von ihm bilden. Dieser Raum wird Kotangentialraum genannt und gewöhnlicherweise mit notiert. Der letzten Definition folgend ist der Raum also isomorph zu . Der Kotangentialraum spielt in der Differentialgeometrie ebenfalls eine sehr wichtige Rolle. So kann man zum Beispiel das totale Differential
- von
als eine lineare Abbildung verstehen, welche jedem Tangentialvektor die Richtungsableitung in seiner Richtung zuordnet. Das totale Differential ist somit ein Element des Kotangentialraums von am Punkt .
Literatur[Bearbeiten | Quelltext bearbeiten]
- Theodor Bröcker: Analysis. Band 3. BI-Wissenschafts-Verlag, Mannheim u. a. 1992, ISBN 3-411-15851-4.
- Klaus Jänich: Vektoranalysis. 5. Auflage. Springer Verlag, Berlin u. a. 2005, ISBN 3-540-23741-0 (Springer-Lehrbuch).
- R. Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, Tensor Analysis and Applications. Springer-Verlag, Berlin u. a. 2003, ISBN 0-201-10168-8.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ John M. Lee: Introduction to Smooth Manifolds. Hrsg.: Springer. 2. Auflage. S. 118.














































































![{\displaystyle \gamma \colon (-\varepsilon ,0]\to M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/306a9fe431290b16c6cbab5f348b6285f0b8bc5b)



