Currying
Currying (vor allem in der Linguistik auch Schönfinkeln) ist die Umwandlung einer Funktion mit mehreren Argumenten in eine Sequenz von Funktionen mit jeweils einem Argument. Obwohl das Verfahren 1924 von Moses Schönfinkel[1] erfunden und von Gottlob Frege[2] um 1900 vorausgedacht wurde, wird es oft nach Haskell Brooks Curry benannt, der das Verfahren 1958 umfangreich theoretisch ausgearbeitet hat.[3]
Verfahren
[Bearbeiten | Quelltext bearbeiten]Es sei eine Funktion gegeben, die n Argumente erfordert. Wird diese auf ein Argument angewendet, so konsumiert sie nur genau dieses und liefert als Funktionswert eine weitere Funktion, die noch Argumente verlangt. Die zurückgegebene Funktion wird anschließend auf alle weiteren Argumente angewendet.
In Typen ausgedrückt, handelt es sich um die Umrechnung einer Funktion zu einer modifizierten Funktion .[4]
Eine alternative Schreibweise ist , wobei als ein Operator verstanden wird, der -stellige Abbildungen (für ) modifiziert zu einer einstelligen Abbildung, deren Bildwerte einstellige Abbildungen sind usw., wobei der Reihe nach alle Argumente der ursprünglichen Abbildung durchlaufen werden; formal:
- .
Das Konzept des Currying ist verwandt mit, aber (für ) verschieden von dem der partiellen Anwendung wie etwa:
- ,
- .
Im einstelligen Fall () hat Currying keine Auswirkung:
- ,
im zweistelligen Fall () besteht der Zusammenhang
- , d. h. für alle :
- ,
im dreistelligen Fall () gilt für :
- , und mit zusätzlich :
- , d. h. ,
allgemein:
- ,
- .[5]
Im Allgemeinen kommt es häufig vor, dass eine mehrstellige Abbildung nicht für alle Wertekombinationen aus den Trägermengen definiert ist, also nur auf einer Teilmenge des kartesischen Produkts , d. h. auf (dem Graphen einer) Relation.[6] Man kann diese Situation behandeln, indem man entweder grundsätzlich partielle Abbildungen zulässt und die obigen Definitionen formal übernimmt, oder man dagegen am Konzept totaler Abbildungen festhält; in letzterem Falle werden die Definitionsbereiche der beteiligten Abbildungen von der Wahl bereits festgelegter Parameter abhängig, wie das Beispiel zweistelliger Abbildungen zeigt:
- ;
der Definitionsbereich dieser Abbildung ist von abhängig:
- ,
also die Urbildfaser von bezüglich des als Relation aufgefassten Definitionsbereichs .[7]
Da für n=1 gilt , kann für dasselbe Symbol verwendet werden wie für . Man nennt dies Überladung (siehe auch Signatur (Modelltheorie) §Anmerkungen).[8]
Beispiele
[Bearbeiten | Quelltext bearbeiten]Lambda-Notation
[Bearbeiten | Quelltext bearbeiten]Ein Beispiel in Lambda-Notation soll das Verfahren verdeutlichen, wobei die Funktion konkret folgendermaßen definiert sei:
Die Funktion verlangt also 3 Argumente und gibt diese zurück. Die Definition ist äquivalent zu:
Bei der Anwendung der Funktion auf die Argumente a, b und c geschieht Folgendes:
Nach erstmaliger Anwendung der Funktion auf a, b und c wird x im Funktionskörper durch das erste Argument a ersetzt. Das Resultat ist eine Funktion, die noch die Argumente y und z verlangt. Diese wird sofort auf b und c angewendet.
Überladung
[Bearbeiten | Quelltext bearbeiten]Angenommen, wir haben eine zweistellige Multiplikationsfunktion , die zwei natürliche Zahlen multipliziert, d. h. einem Paar natürlicher Zahlen ihr Produkt zuordnet:
- mit [9]
Per Definition wird diese Funktion auf zwei natürliche Zahlen angewendet und eine natürliche Zahl wird zurückgegeben, beispielsweise .
Wird nun zunächst das erste Argument besetzt (etwa mit ), das zweite noch freigelassen, entsteht eine einstellige ‚höhere Funktion‘, die selbst ein (weiteres) Argument aufnimmt und das Produkt mit diesem festen Parameter (der Nummer ) zurückgibt:
- ,
und für ein beliebiges festes erstes Argument :
- .
Currying bedeutet nun bei einer n-stelligen Funktion, diesen Vorgang so lange durchzuführen, bis nur eine noch einstellige höhere Funktion übrigbleibt. Für n = 2 ist daher:
Da die Bezeichnung als einstellige Funktion noch unbesetzt ist, kann diese überladen werden,[11] d. h., im einstelligen Fall wird als verstanden:
- .
Geometrisches Beispiel
[Bearbeiten | Quelltext bearbeiten]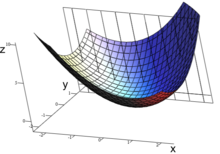
Man kann sich die Situation für eine Funktion mit zwei Argumenten wie folgt vorstellen: das Fixieren einer Argumentvariable entspricht einer Einschränkung der zweidimensionalen Definitionsmenge auf eine eindimensionale Teilmenge, z. B. , die resultierende Funktion entspricht der Schnittkurve des Graphen von mit der Ebene aller Punkte . Alle Punkte des Graphen können somit auch durch eine zweistufige Auswahl erreicht werden: zunächst durch die Festlegung der Schnittebene und dann durch die Auswertung der Schnittkurve an der Stelle .
Anwendung
[Bearbeiten | Quelltext bearbeiten]Currying wird überwiegend in Programmiersprachen und Kalkülen verwendet, in denen Funktionen nur ein einzelnes Argument erhalten dürfen. Dazu gehören beispielsweise ML, Unlambda und der Lambda-Kalkül sowie das nach Curry benannte Haskell. Viele dieser Sprachen bieten dem Programmierer allerdings syntaktische Möglichkeiten, dies zu verschleiern. Ein Beispiel hierfür ist die Äquivalenz der Funktionsdefinition im oben gezeigten Beispiel.
Das nachfolgende Beispiel zeigt Currying in JavaScript. Zunächst wird eine Funktion uncurried_add definiert, die als Ergebnis die Summe der beiden Argumente hat. Andererseits wird eine Funktion curried_add definiert, die eine als Closure definierte Funktion zurückgibt, welche partiell angewendet werden kann.
function uncurried_add(x, y) {
return x + y;
}
function curried_add(x) {
return function(y) {
return x + y;
};
}
console.log(uncurried_add(3, 5)); // 8
console.log(curried_add(3)(5)); // 8
const add_three = curried_add(3);
console.log(add_three(5)); // 8
console.log(add_three(12)); // 15
Durch Currying wird die Funktion partiell angewendet, wobei die Funktionsargumente nacheinander übergeben werden und zwischenzeitlich in einer neuen Funktion gehalten werden, die beliebig weiterverwendet werden kann.
Die Funktionen können in JavaScript mit der Lambda-Notation auch kürzer definiert werden:
const uncurried_add = (x, y) => x + y;
const curried_add = x => y => x + y;
Geläufig ist in JavaScript auch das Currying durch apply, eine Methode des Prototyps von Funktionen, der ein Kontextobjekt und eine Teilmenge der Parameter übergeben werden. Das Kontextobjekt kann dabei null oder undefined sein und wird dann implizit durch das globale Objekt ersetzt:[12]
function uncurried_add(x, y) {
return x + y;
}
const curried_add = uncurried_add.bind(null, 3);
console.log(curried_add(5)); // 8
import java.util.function.*;
class Main {
static IntBinaryOperator uncurriedAdd = (x, y) -> x + y;
static IntFunction<IntUnaryOperator> curriedAdd = x -> y -> x + y;
public static void main(String[] args) {
System.out.println(uncurriedAdd.applyAsInt(3, 5)); // 8
System.out.println(curriedAdd.apply(3).applyAsInt(5)); // 8
var addThree = curriedAdd.apply(3);
System.out.println(addThree.applyAsInt(5)); // 8
System.out.println(addThree.applyAsInt(12)); // 15
}
}
val uncurried_add = { x: Int, y: Int -> x + y }
val curried_add = { x: Int -> { y: Int -> x + y } }
println(uncurried_add(3, 5)) // 8
println(curried_add(3)(5)) // 8
val add_three = curried_add(3)
println(add_three(5)) // 8
println(add_three(12)) // 15
C++ führte den Lambda-Kalkül mit anonymen Funktionen in die Sprache ein. Mit dem Schlüsselwort auto wird durch Typinferenz der Datentyp implizit abgeleitet, ohne den Datentypen explizit deklarieren zu müssen. Dadurch ergibt sich eine kürzere Schreibweise für die Currifizierung:
#include <iostream>
using namespace std;
int uncurried_add(int x, int y) {
return x + y;
}
auto curried_add(int x) {
return [x](int y) { return x + y; };
}
int main() {
cout << uncurried_add(3, 5) << endl; // 8
cout << curried_add(3)(5) << endl; // 8
auto add_three = curried_add(3);
cout << add_three(5) << endl; // 8
cout << add_three(12) << endl; // 15
return 0;
}
Man beachte, dass die Erwähnung des Typs int im Argument des Lambda-Ausdrucks auch durch auto ersetzt werden kann, wodurch die Implementierung verallgemeinert wird. Die Parameter der benannten Funktion curried_add kann jedoch nur durch Templates für verschiedene Datentypen verallgemeinert werden.
Da es in der Programmiersprache C keine anonymen Funktionen gibt, wird eine benannte Funktion add separat definiert, die von curried_add zurückgegeben wird. Der Wert von x wird in der globalen Variablen z gespeichert, da die Funktion add nicht auf die Continuation der Funktion curried_add zugreifen kann.
#include <stdio.h>
int uncurried_add(int x, int y) {
return x + y;
}
int z;
int add(int y) {
return y + z;
}
typedef int function(int);
function* curried_add(int x) {
z = x;
return add;
}
int main() {
printf("%d\n", uncurried_add(3, 5)); // 8
printf("%d\n", curried_add(3)(5)); // 8
function* add_three = curried_add(3);
printf("%d\n", add_three(5)); // 8
printf("%d\n", add_three(12)); // 15
return 0;
}
using System;
class Program {
delegate int Method(int x, int y);
delegate Func<int, int> Curry(int x);
static Method uncurried_add = (x, y) => x + y;
static Curry curried_add = x => y => x + y;
public static void Main() {
Console.WriteLine(uncurried_add(3, 5)); // 8
Console.WriteLine(curried_add(3)(5)); // 8
var add_three = curried_add(3);
Console.WriteLine(add_three(5)); // 8
Console.WriteLine(add_three(12)); // 15
}
}
let uncurried_add (x, y) = x + y
let curried_add x y = x + y
printfn "%i" (uncurried_add (3, 5)) // 8
printfn "%i" ((curried_add 3) 5) // 8
printfn "%i" (curried_add 3 5) // 8
let add_three = curried_add 3
printfn "%i" (add_three 5) // 8
printfn "%i" (add_three 12) // 15
package main
import "fmt"
var uncurried_add = func(a, b int) int {
return a + b
}
var curried_add = func(a int) func(a int) int {
return func(b int) int {
return a + b
}
}
func main() {
fmt.Println(uncurried_add(2, 3))
fmt.Println(curried_add(2)(3))
addThree := curried_add(3)
fmt.Println(addThree(5)) // 8
fmt.Println(addThree(12)) // 15
}
In der Programmiersprache Haskell kann eine Funktion nur genau einen Parameter haben. Wenn man eine Funktion mit mehreren Argumenten aufrufen möchte, müssen die Argumente zuerst in einem neuen Objekt zusammengesetzt werden, sodass die Funktion nur ein Argument erhält. Dafür können die Parameter in runden Klammern mit Kommata getrennt aufgelistet werden, um ein Tupel zu definieren.
uncurried_add (x, y) = x + y
Eine Alternative dazu ist das Currying. In der expliziten Schreibweise definiert man für jeden Wert im Tupel jeweils eine Funktion mit nur einem Argument. Solange noch nicht alle Argumente übergeben wurden, wird eine Funktion zurückgegeben, die ein Teilergebnis liefert.
curried_add x = \y -> x + y
Da die Schreibweise mit mehreren Lambda-Funktionen umständlich sein kann, gibt es eine syntaktisch gezuckerte Notation, die semantisch äquivalent ist. Schreibt man die Argumente ohne runde Klammern hintereinander, erhält man automatisch eine currifizierte Funktion.
curried_add x y = x + y
Die currifizierte Funktion kann sowohl explizit, als auch implizit partiell angewendet werden.
main = do
print (uncurried_add (3, 5)) -- 8
print ((curried_add 3) 5) -- 8
print (curried_add 3 5) -- 8
let add_three = curried_add 3
print (add_three 5) -- 8
print (add_three 12) -- 15
Zudem gibt es in Haskell die Möglichkeit eine Funktion im Nachhinein zwischen currifizierter und nicht currifizierter Definition umzuwandeln. Dafür werden die Funktionen curry und uncurry verwendet.
main = do
let uncurried = uncurry curried_add
print (uncurried (3, 5)) -- 8
let curried = curry uncurried_add
print ((curried 3) 5) -- 8
print (curried 3 5) -- 8
let add_three = curried 3
print (add_three 5) -- 8
print (add_three 12) -- 15
def uncurried_add(x, y):
return x + y
def curried_add(x):
return lambda y: x + y
print(uncurried_add(3, 5)) # 8
print(curried_add(3)(5)) # 8
add_three = curried_add(3)
print(add_three(5)) # 8
print(add_three(12)) # 15
sub uncurried_add($x, $y) { $x + $y }
sub curried_add($x) {
sub ($y) { $x + $y };
}
say uncurried_add(3, 5); # 8
say curried_add(3)(5); # 8
my &add_three = &curried_add(3);
say &add_three(5); # 8
say &add_three(12); # 15
Es gibt in der Programmiersprache Raku die Möglichkeit, ein Funktionsobjekt erst beim Funktionsaufruf zu currifizieren.
my &uncurried_add = sub ($x, $y) { $x + $y };
say &uncurried_add(3, 5); # 8
say &uncurried_add.assuming(3)(5); # 8
my &add_three = &uncurried_add.assuming(3);
say &add_three(5); # 8
say &add_three(12); # 15
def uncurried_add(x, y)
return x + y
end
def curried_add(x)
return lambda { |y| x + y }
end
puts uncurried_add(3, 5) # 8
puts curried_add(3).call(5) # 8
add_three = curried_add(3)
puts add_three.call(5) # 8
puts add_three.call(12) # 15
Es gibt in der Programmiersprache Ruby die Möglichkeit, ein Funktionsobjekt erst beim Funktionsaufruf zu currifizieren.
uncurried_add = lambda { |x, y| x + y }
puts uncurried_add.call(3, 5) # 8
puts uncurried_add.curry[3][5] # 8
add_three = uncurried_add.curry[3]
puts add_three.call(5) # 8
puts add_three.call(12) # 15
(define uncurried-add (lambda (x y)
(+ x y)))
(define curried-add (lambda (x)
(lambda (y)
(+ x y))))
(display (uncurried-add 3 5)) (newline) ; 8
(display ((curried-add 3) 5)) (newline) ; 8
(define add-three (curried-add 3))
(display (add-three 5)) (newline) ; 8
(display (add-three 12)) (newline) ; 15
Tcl
[Bearbeiten | Quelltext bearbeiten]In Tcl ist es nicht notwendig, irgendwelche speziellen Konstrukte als curried- oder uncurried-Variante vorzubereiten.
Ein Kommando-Aufruf ist in Tcl nur eine Liste von Worten, in der das Kommando-Wort an erster Position steht. Mit dem Operator {*} kann man ein Argument, das seinerseits eine Liste ist, inplace durch deren Elemente ersetzen. Damit kann eine beim Aufruf an vorderster Position stehende Liste neben dem zu rufenden Kommando zusätzlich beliebig viele Argumente in sich tragen.
Currying ist demzufolge identisch mit dem Anhängen eines weiteren Wortes an diese Liste, und jeder mit {*} beginnende Aufruf ist ein Lambda-Call (Benannt nach den in anderen Sprachen oft „Lambda-Ausdruck“ genannten anonymen Funktionen, die sich gut auf diese Weise einbinden lassen).
Zum Addieren ist hier das Standard-Kommando tcl::mathop::+ verwendet, das zur Implementierung der hier nicht benutzten Tcl-Expression-Syntax existiert. Dieses Kommando addiert beliebig viele Argumente.
Da man solche Experimente sinnvollerweise in der Tcl-Konsole anstellt, sind hier keine expliziten print-Anweisungen nötig.
tcl::mathop::+ 3 5 ;# 8 direkter Aufruf
set f tcl::mathop::+ ;# simple "Lambda"-Liste, nur das Kommando
{*}$f 3 5 ;# 8 Aufruf über "Lambda" in Variable f
lappend f 3 ;# "Currying" durch Hinzufügen
set f {tcl::mathop::+ 3} ;# "Curried" alternativ direkt formuliert
{*}$f 5 ;# 8 Aufruf über "Curried Lambda"
lappend f 1 2 ;# mehr Parameter hinzufügen
{*}$f 4 5 ;# 15 = (3+1+2) + (4+5) ... ganz natürlich
Delphi
[Bearbeiten | Quelltext bearbeiten]program curried;
{$APPTYPE CONSOLE}
{$R *.res}
uses
System.SysUtils;
function uncurried_add(a, b: Integer): Integer;
begin
Result := a + b;
end;
function curried_add(a: Integer): TFunc<Integer, Integer>;
begin
Result := function(b: Integer): Integer
begin
Result := a + b;
end;
end;
begin
Writeln(uncurried_add(3, 5)); // 8
Writeln(curried_add(3)(5)); // 8
var addThree := curried_add(3);
Writeln(addThree(5)); // 8
Writeln(addThree(12)); //15
end.
Einzelnachweise und Anmerkungen
[Bearbeiten | Quelltext bearbeiten]- ↑ Moses Schönfinkel: Über die Bausteine der mathematischen Logik. In: Mathematische Annalen 92 (1924). S. 305–316, Digitalisat.
- ↑ Gottlob Frege: Grundgesetze der Arithmetik. Hermann Pohle, Jena 1893 (Band I) 1903 (Band II) korpora.org ( vom 28. Oktober 2022 im Internet Archive).
- ↑ Haskell Brooks Curry, Robert Feys, Roger Hindley, Jonathan P. Seldin: Combinatory Logic. North Holland, 2 Bände, 1958, 1972.
- ↑ Dabei bezeichnet oder die Menge der Abbildungen von nach .
- ↑ Im nullstelligen Fall (n=0) würde das Currying einer Abbildung ohne Parameter und mit einem Wert eine einstellige Abbildung mit konstantem Wert zuordnen, also etwa
- .
- ↑ Ein Beispiel ist mit (wobei die Diagonale bezeichnet).
- ↑ Im obigen Beispiel ist dies .
- ↑ Voraussetzung ist, dass das Symbol nicht schon anderweitig mit Stelligkeit 1 überladen ist (siehe Beispiel unten, dies zwingt zwischen und zu unterscheiden).
- ↑ Zur Unterscheidung vom Platzhalter wird hier als Multiplikationszeichen verwendet.
- ↑ Dieser Funktion könnte man auch einen eigenen Namen vergeben:
- ↑ Man unterscheide zwischen und der überladenen Funktion mit zur Stelligkeit und Faktoren . Zwar ist zweistellig , aber einstellig ist , während eine einstellige Funktion ist.
- ↑ Kyle Simpson: this & Object Prototypes. In: You Don't Know JS. 1. Auflage. Band 3. O’Reilly, 2014, ISBN 978-1-4919-0415-2, S. 26–28.


























































![{\displaystyle [X\to Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87e4e00b8a33bbcb979900f5b33917e320f9067b)




















