Selbstähnlichkeit
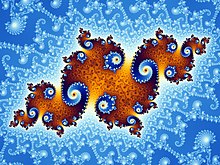
Selbstähnlich ist ein System, das seinen Elementen ähnelt. Diese Eigenschaft wird unter anderem von der fraktalen Geometrie untersucht, da fraktale Objekte eine hohe Selbstähnlichkeit aufweisen.
Im weiteren Sinne wird der Begriff auch in der Philosophie sowie den Sozial- und Naturwissenschaften verwendet, um grundsätzlich wiederkehrende, in sich selbst verschachtelte Strukturen zu bezeichnen.
Beispiele
[Bearbeiten | Quelltext bearbeiten]

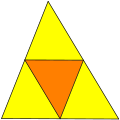
Bei Fraktalen ist von exakter (oder strikter) Selbstähnlichkeit die Rede, wenn bei unendlicher Vergrößerung des untersuchten Objekts immer wieder die ursprüngliche Struktur erhalten wird, ohne jemals eine elementare Feinstruktur zu erhalten. Exakte Selbstähnlichkeit ist praktisch nur bei mathematisch – z. B. durch ein iteriertes Funktionen-System – erzeugten Objekten zu finden. Beispiele dafür sind das Sierpinski-Dreieck, die Koch-Kurve, die Cantor-Menge oder trivialerweise ein Punkt und eine Gerade.
In den nachfolgenden zwölf weiteren Beispielen sind für verschiedene jeweils die ersten verkleinerten Versionen der Ausgangsfigur dargestellt, die im Englischen auch als Reptiles (Abkürzung für replicating tiles) bezeichnet werden. Die zusammengesetzte Figur wird rep--Figur genannt.[1][2]
-
Figur 1: Allgemeines Dreieck
-
Figur 2: Allgemeines Dreieck
-
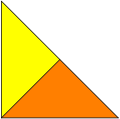
Figur 3: gleichschenklig-rechtwinkliges Dreieck
-
Figur 4: Dreieck mit den Innenwinkeln 30°, 60° und 90°
-
Figur 5: Rechtwinkliges Dreieck, bei dem eine Kathete die doppelte Länge der anderen hat
-
Figur 6: Gleichschenkliges Trapez
-
Figur 7: Gleichschenkliges Trapez
-
Figur 8: "Sphinx tiling"
-
Figur 9: "Sphinx tiling"
-
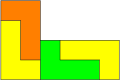
Figur 10: L-Tromino
-
Figur 11: L-Tetromino
-
Figur 12: T-Tetromino
Die Mandelbrot-Menge und die Julia-Mengen sind selbstähnlich, nicht jedoch strikt selbstähnlich. Strikte Selbstähnlichkeit impliziert Skaleninvarianz und lässt sich unter anderem mit Hilfe der charakteristischen Exponenten des zugrundeliegenden Potenzgesetzes (Skalengesetzes) quantifizieren.
Ähnlichkeits-Dimension
[Bearbeiten | Quelltext bearbeiten]Berechnung
[Bearbeiten | Quelltext bearbeiten]Für selbstähnliche Mengen, die aus um den Faktor verkleinerten Versionen ihrer selbst bestehen, ist die Ähnlichkeitsdimension
definiert. Man beachte, dass man hier keinen Grenzwert braucht.
Beispiele
[Bearbeiten | Quelltext bearbeiten]Ein Quadrat besteht aus 4 Quadraten () der halben () Seitenlänge und hat damit die Ähnlichkeitsdimension .
Das Sierpinski-Dreieck besteht aus um den Faktor verkleinerten Kopien seiner selbst. Seine Ähnlichkeits-Dimension ist .[3]
Die Koch-Kurve besteht aus um den Faktor verkleinerten Kopien ihrer selbst. Ihre Ähnlichkeits-Dimension ist .[4]
Aber schon ein Kreis besteht nicht aus verkleinerten Kreisen, und die Ähnlichkeitsdimension ist nicht definiert. Die fraktale Dimension vieler bekannter Fraktale lässt sich aber damit bestimmen. Aufgrund der fehlenden Grenzwertbildung ist die Ähnlichkeitsdimension besonders einfach und ist deshalb oft die einzige für Laien verständliche fraktale Dimension. Diese Methode der Dimensionsberechnung drängt sich insbesondere auch bei IFS-Fraktalen auf.
Natur
[Bearbeiten | Quelltext bearbeiten]
Real existierende Beispiele wären z. B. die Verästelung von Blutgefäßen, Farnblättern oder Teile eines Blumenkohls (das wird bei der Sorte Romanesco sehr deutlich), die in einfacher Vergrößerung dem Blumenkohlkopf sehr ähnlich sind. Bei realen Beispielen lässt sich die Vergrößerung nicht bis ins Unendliche fortsetzen, wie es bei idealen Objekten der Fall ist.
Auch beliebige Abbildungen der realen Welt weisen Selbstähnlichkeiten auf, die z. B. bei der fraktalen Bildkompression oder der fraktalen Tonkompression genutzt werden.
Die Rekurrenzen bezeichnen den Aufruf oder die Definition einer Funktion durch sich selbst, die demzufolge selbstähnlich sind.
Die Selbstähnlichkeit ist ein Phänomen, das oft in der Natur auftritt. Eine kennzeichnende Zahl für die immer wiederkehrende Selbstähnlichkeit ist der Goldene Schnitt.
Auch die Trajektorien eines Wiener-Prozesses sowie der gebrochenen Brownschen Bewegung sind selbstähnlich.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Henning Fernau: Iterierte Funktionen, Sprachen und Fraktale. B. I. Wissenschaftsverlag, Mannheim – Wien – Zürich 1994, ISBN 3-411-17011-5.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Landschaftsfotos zum Maßstabsproblem ( vom 20. Januar 2014 im Internet Archive)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik - 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen, Springer Spektrum, Springer-Verlag GmbH Berlin Heidelberg 2015, ISBN 978-3-662-45460-2, Seiten 51 bis 54
- ↑ George E. Martin: Polyominoes: A Guide to Puzzles and Problems in Tiling, AMS/MAA, Washington 1991
- ↑ Wolfram MathWorld: Sierpiński Sieve
- ↑ Wolfram MathWorld: Koch Snowflake