Koch-Kurve
Die Koch-Kurve oder kochsche Kurve ist ein von dem schwedischen Mathematiker Helge von Koch 1904 vorgestelltes Beispiel für eine überall stetige, aber nirgends differenzierbare Kurve. Es handelt sich bei ihr ferner um eines der ersten formal beschriebenen fraktalen Objekte. Die Koch-Kurve ist eines der am häufigsten zitierten Beispiele für ein Fraktal und wurde bei der Entdeckung als Monsterkurve bezeichnet. Die Koch-Kurve ist auch in Form der kochschen Schneeflocke bekannt, die durch geeignete Kombination dreier Koch-Kurven entsteht.
Konstruktion[Bearbeiten | Quelltext bearbeiten]
Man kann die Kurve anschaulich mittels eines iterativen Prozesses konstruieren (siehe Lindenmayer-System). Zu Beginn besteht die Kurve aus einem einzigen Streckenstück. Die Iteration besteht nun darin, dass dieser Streckenabschnitt durch einen anderen, aus 4 gleich langen Strecken bestehenden Streckenabschnitt ersetzt wird. Die Winkel zwischen diesen Strecken betragen 240°, 60° und 240°. Jeder der 4 neuen Streckenabschnitte hat der Länge des ursprünglichen Streckenabschnitts. Im nächsten Schritt wird jeder der 4 Streckenabschnitte durch einen Streckenabschnitt der oberen Art ersetzt.
Diese Iteration wird nun beliebig oft wiederholt, wobei die Dreiecke stets zur selben Seite der Kurve hin zu errichten sind. Auf diese Weise ergibt sich eine Folge von Streckenzügen, die gegen die Koch-Kurve strebt.
Graphische Darstellung der Konstruktion[Bearbeiten | Quelltext bearbeiten]
Die ersten drei Iterationen der Konstruktion sehen so aus: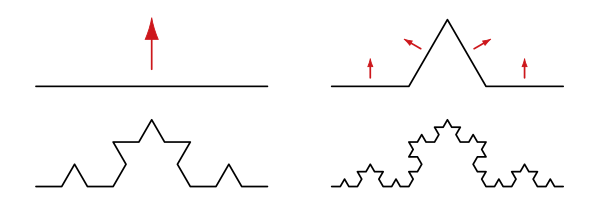
Nach fünf Iterationen ergibt sich folgendes Bild:
Dieses Konstruktionsprinzip, bei dem iterativ jede Teilstrecke durch einen Streckenzug ersetzt wird, lässt sich auch für die Erzeugung anderer fraktaler Kurven verwenden. So wird es beispielsweise bei der Drachenkurve eingesetzt.
Das Konstruktionsprinzip ist eng verwandt mit dem der Erzeugung der Cantor-Menge, welche man erhält, wenn man das mittlere Drittel der Strecke nicht ersetzt, sondern entfernt.
Lindenmayer-System[Bearbeiten | Quelltext bearbeiten]
Die Koch-Kurve lässt sich durch ein Lindenmayer-System mit folgenden Eigenschaften beschreiben:
- Winkel: 60°
- Startstring:
- Ableitungsregeln:
Wählt man als Startstring (ein gleichseitiges Dreieck), so erhält man die kochsche Schneeflocke.
Definition des Grenzwerts[Bearbeiten | Quelltext bearbeiten]
Der Grenzwert dieser Iteration (z. B. als IFS-Fraktal), die eigentliche Koch-Kurve, ist in gewissem Sinne unendlich fein strukturiert und kann daher nur näherungsweise grafisch dargestellt werden. In diesem Fall lässt sich der Grenzwert einfach wie folgt definieren:
- Zum Grenzwert der Iteration gehören diejenigen Punkte, die von irgendeinem Iterationsschritt an in allen folgenden Iterationen enthalten sind, sowie alle Häufungspunkte der so gebildeten Punktmenge.
Der linke Endpunkt des anfänglichen Streckenstücks ist beispielsweise in jeder Iteration enthalten und gehört damit zur Koch-Kurve. Der Mittelpunkt des anfänglichen Streckenstücks hingegen ist schon ab der ersten Iteration nicht mehr enthalten. Eine andere gleichbedeutende Grenzwertdefinition ist weiter unten durch die Parameterdarstellung gegeben.
Alternative Definitionen[Bearbeiten | Quelltext bearbeiten]
Der iterative Prozess für die Koch-Kurve kann auch auf andere Weise definiert werden:
- Begonnen wird mit einer einzigen Strecke (Bild 1). Auf dem mittleren Abschnitt jeder Teilstrecke wird ein regelmäßiges Sechseck aufgesetzt, dessen Seitenlänge der Länge der Strecke beträgt. Für einige Teilstrecken ergibt sich dabei das gleiche regelmäßige Sechseck. Die dadurch entstehende Fläche ist die Fläche unterhalb der Koch-Kurve.[1]
- Die Startfigur ist ein regelmäßiges Sechseck (Bild 2). Jede Teilstrecken wird durch einen anderen, aus 4 gleich langen Strecken bestehenden Streckenabschnitt ersetzt, wobei die Strecken die Winkel 120°, 300° und 120° bilden.[2] Diese Streckenabschnitte sind also genauso definiert wie bei der oben beschriebenen Konstruktion mit dem Unterschied, dass der zweite und dritte Streckenabschnitt nach innen gerichtet ist. Ist die Seitenlänge des regelmäßigen Sechsecks, dann hat es den Flächeninhalt . Der Flächeninhalt der 6 gleichseitigen Dreiecke, die beim ersten Iterationsschritt abgezogen werden, beträgt zusammen . Mit jedem Schritt vervierfacht sich die Anzahl der abgezogenen Dreiecke, während der Flächeninhalt um den Faktor kleiner wird. Der Flächeninhalt der abgezogenen Dreiecke wird also mit jedem Schritt um den Faktor kleiner, beträgt nach dem Iterationsschritt also . Mithilfe der geometrischen Reihe ergibt sich, dass der gesamte Flächeninhalt dieser Dreiecke für eine sehr große Anzahl von Schritten dem Grenzwert nähert. Der Flächeninhalt innerhalb des Streckenzugs nähert sich also dem Grenzwert . Als Fläche ergibt sich die kochsche Schneeflocke.

Dreieck 30°, 30°und 120°, 5 Iterationsschritte
- Die Startfigur ist ein gleichschenkliges Dreieck mit den Innenwinkeln 30°, 30° und 120° (Bild 3). Aus diesem Dreieck wird ein gleichseitiges Dreieck herausgeschnitten, dessen Seitenlänge der längsten Seite des gleichschenkligen Dreiecks ist. Dabei entstehen 2 neue gleichschenklige Dreiecke mit der Seitenlängen. Mit jedem Iterationsschritt werden wiederum gleichseitige Dreiecke aus jedem gleichschenkligen Teildreieck herausgeschnitten, sodass sich der Flächeninhalt um den Faktor verringert. Die übrigbleibende Fläche nähert sich dabei der Koch-Kurve an.[3]
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Eigenschaften aus der fraktalen Geometrie[Bearbeiten | Quelltext bearbeiten]
Die Koch-Kurve ist nach ihrer Konstruktionsvorschrift streng selbstähnlich, das heißt, es erscheinen bei beliebiger Vergrößerung immer wieder die gleichen Strukturen. Sie hat eine Hausdorff-Dimension von
Länge und Flächeninhalt[Bearbeiten | Quelltext bearbeiten]
Die Länge der ursprüngliche Strecke, die die beiden Enden der Kurve verbindet, sei .
Bei jedem Iterationsschritt wird jede Strecke des Streckenzugs durch 4 Strecken mit der Streckenlänge ersetzt. Die Kurve wird also mit jedem Iterationsschritt um den Faktor länger. Nach dem Iterationsschritt ist die Kurvenlänge also um den Faktor angewachsen und beträgt . Wegen divergiert die Kurvenlänge, d. h. sie geht gegen unendlich.
Die Fläche unterhalb der Kurve ist hingegen begrenzt, d. h. der Flächeninhalt konvergiert. Das gleichseitige Dreieck, das nach dem ersten Iterationsschritt hinzukommt, hat den Flächeninhalt . Mit jedem Schritt vervierfacht sich die Anzahl der hinzugefügten Dreiecke, während der Flächeninhalt um den Faktor kleiner wird. Der Flächeninhalt der hinzugefügten Dreiecke wird also mit jedem Schritt um den Faktor kleiner, beträgt nach dem Iterationsschritt also . Der gesamte Flächeninhalt nach dem Iterationsschritt unterhalb der Kurve berechnet sich mithilfe der geometrische Reihe zu
Für eine sehr große Anzahl von Schritten nähert sich dieser Flächeninhalt dem Grenzwert
Bei der kochschen Schneeflocke werden die 3 Seiten eines gleichseitige Dreiecks mit der Seitenlänge durch die Koch-Kurve ersetzt. Der Flächeninhalt, der von der kochschen Schneeflocke eingeschlossen wird, ergibt sich also, indem man das Dreifache des Flächeninhalts unterhalb der Koch-Kurve zum Flächeninhalt des gleichseitigen Dreiecks addiert:[4]
Stetigkeit und Differenzierbarkeit[Bearbeiten | Quelltext bearbeiten]
Die Kurve ist überall stetig, aber nirgends differenzierbar.
Zur Untersuchung dieser Eigenschaften betrachtet man die Parameterdarstellung des Iterationsschritts und deren Grenzfunktion . Wenn man als Zeitpunkt auffasst, ist derjenige Punkt auf dem Streckenzug nach dem Iterationsschritt , den man zum Zeitpunkt erreicht, wenn man den Streckenzug mit konstanter Geschwindigkeit (allerdings mit abrupten Richtungsänderungen) vom linken zum rechten Endpunkt durchläuft. Die Funktionen sind alle stetig und konvergieren punktweise gegen die Grenzfunktion .
Stellt man den Zeitpunkt in einer Entwicklung zur Basis 4 dar, d. h. mit den Ziffern 0, 1, 2, 3, dann gibt die erste Nachkommastelle den Abschnitt des ersten Konstruktionsschrittes an, auf welchem sich befindet, die zweite den Unterabschnitt auf diesem im zweiten Konstruktionsschritt usw. Dadurch kann man mit den ersten Nachkommastellen ein Gebiet der Größenordnung konstruieren, in welchem sich alle nachfolgenden Punkte aufhalten müssen. Aus dieser Eigenschaft folgt, dass die Funktionen sogar gleichmäßig gegen konvergieren. Nach einem Satz der Analysis ist als „gleichmäßiger Limes stetiger Funktionen“ dann ebenfalls stetig.
In jedem noch so kleinen Abschnitt der Kurve finden sich nach der Konstruktion Teilstücke, die eine Richtung für jedes haben. Daher kann man zu keinem Punkt der Kurve eine Tangente konstruieren, d. h. die Kurve ist nirgends differenzierbar.
Kochsche Schneeflocke[Bearbeiten | Quelltext bearbeiten]
Beginnt man den Ersetzungsprozess der Koch-Kurve nicht mit einer Strecke, sondern mit einem gleichseitigen Dreieck, dann erhält man die kochsche Schneeflocke. Sie besteht aus drei Koch-Kurven und schließt trotz ihrer unendlichen Länge nur einen Bereich mit endlicher Fläche ein. Die kochsche Schneeflocke ist im Gegensatz zur Koch-Kurve nicht selbstähnlich. Sie ist spiegelsymmetrisch, punktsymmetrisch und drehsymmetrisch.

Parkettierungen[Bearbeiten | Quelltext bearbeiten]
Die euklidische Ebene kann mit kochschen Schneeflocken mit zwei verschiedenen Größen parkettiert werden (siehe Abbildung). Diese Parkettierung ist periodisch, spiegelsymmetrisch, punktsymmetrisch, drehsymmetrisch und translationssymmetrisch.
Dabei sind die Abmessungen der großen Schneeflocken um den Faktor größer als die kleinen Schneeflocken. Der Flächeninhalt ist also 3-mal so groß.
Es ist möglich, eine kochsche Schneeflocke in 6 Schneeflocken mit des Flächeninhalts und 1 Schneeflocke mit des Flächeninhalts zu zerlegen. Daher gibt es auch Parkettierungen mit kochschen Schneeflocken, die mehr als zwei verschiedene Größen haben.
Anwendung[Bearbeiten | Quelltext bearbeiten]
- Ein Beispiel ist die Fraktalantenne
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Die kochsche Schneeflocke kann auch mithilfe eines Hexagramms definiert werden. Startfigur ist dann ein Hexagramm. Mit jedem Iterationsschritt wird jeder Streckenabschnitt durch einen aus 4 gleich langen Strecken bestehenden Streckenabschnitt mit den Winkeln , und ersetzt. Als Verallgemeinerung kann als Startfigur ein -Stern genommen werden. Dabei bezeichnet das Schläfli-Symbol. Dann wird mit jedem Iterationsschritt jeder Streckenabschnitt durch einen aus 4 gleich langen Strecken bestehenden Streckenabschnitt mit den Winkeln , und ersetzt.

Startfigur Achtort (0, hellblau) mit 2 Iterationsschritten.

Startfigur Pentagramm (0, hellblau) mit 3 Iterationsschritten.

Für den Fall ist die Startfigur ein Pentagramm[5] und die Winkel zwischen den Strecken betragen , und .
Die Animation (Bild 4) zeigt einen Ausschnitt der kochschen Schneeflocke für . In der nächsten Darstellung (Bild 5) sind auf einer Zacke der Startfigur (0, hellblau) die drei ausgeführten Iterationsschritte farbig hervorgehoben: 1. Iterationsschritt (goldgelb), 2. Iterationsschritt (grün) und 3. Iterationsschritt (rot).
Der Flächeninhalt dieser verallgemeinerten kochschen Schneeflocke beträgt , wobei die Seitenlänge des Pentagramms bezeichnet.[6]
Für den Fall (Bild 6) ist die Startfigur ein Achtort und die Winkel zwischen den Strecken betragen und . Auf einer Zacke der Startfigur (0, hellblau) sind die zwei ausgeführten Iterationsschritte farbig hervorgehoben: 1. Iterationsschritt (hellgrün), 2. Iterationsschritt (rot). Der Flächeninhalt innerhalb der Kurve beträgt .
Lokalisierung von Punkten[Bearbeiten | Quelltext bearbeiten]
Wird das Einheitsintervall äquidistant auf die Koch-Kurve abgebildet, dann gibt es ein effektives Verfahren, um herauszufinden, auf welchen Punkt eine reelle Zahl mit abgebildet wird. Dafür wird die Darstellung von im Dualsystem verwendet und anschließend das gleichschenklige Dreieck mit den Innenwinkeln 30°, 30° und 120°, in dem die Koch-Kurve liegt, Schritt für Schritt verkleinert (siehe Alternative Definitionen).
Beispiel[Bearbeiten | Quelltext bearbeiten]

Es soll der Punkt ermittelt werden, auf den die Zahl 0,625 abgebildet wird. Die Zahl 0,625 hat im Dualsystem die Darstellung . Im ersten Schritt wird aus dem gleichschenkligen Dreieck ein gleichseitiges Dreieck herausgeschnitten, dessen Seitenlänge der längsten Seite des gleichschenkligen Dreiecks ist. Dabei entstehen 2 neue gleichschenklige Dreiecke mit der Seitenlängen. Der Punkt liegt dann innerhalb des rechten gleichschenkligen Dreiecks, weil die erste duale Nachkommastelle gleich 1 ist. Im zweiten Schritt entstehen wieder 2 neue gleichschenklige Dreiecke mit kleinerer Seitenlänge. Der Punkt liegt innerhalb des linken gleichschenkligen Teildreiecks, weil die zweite duale Nachkommastelle gleich 0 ist. Im dritten Schritt liegt der Punkt im rechten Teildreieck, weil die dritte duale Nachkommastelle gleich 1 ist. Alle weiteren Nachkommastellen sind gleich 0. Daher liegt der gesuchte Punkt P zum Punkt A orientiert, ist also die obere Ecke dieses Teildreiecks (siehe Abbildung).
Die Grundlage dieses Algorithmus ist im Abschnitt Alternative Definitionen zu finden.
Bemerkung: Ein solches Verfahren lässt sich im Prinzip auch auf andere "einfache" kurvenförmige und selbstähnliche Fraktale, wie zum Beispiel die Hilbert-Kurve, die Peano-Kurve, die Gosper-Kurve und Minkowski-Kurve anwenden. Das kurvenförmige Fraktal muss dabei nicht in zwei Dimensionen verlaufen. Entscheidend ist jedoch die äquidistante Ordnungsrelation der selbstähnlichen Kurve. Bei selbstaffinen Fraktalen ist die Zuordnung des Einheitsintervalls zu den Koordinaten komplizierter. Für mehrdimensionale selbstähnliche Fraktale, wie zum Beispiel das Sierpinski-Tetraeder, den Menger-Schwamm oder deren Oberfläche, für die keine eindeutige Ordnungsrelation definiert ist, ist das nicht ohne Weiteres möglich.
Die Abbildung des Einheitsintervalls auf ein "einfaches" kurvenförmiges (oder selbstaffines Fraktal) kann mithilfe von einfachen geometrischen Betrachtungen passieren. Im Fall der Schneeflockenkurve kann es wie beschrieben, die iterative Erzeugung von 30°-120°-30°-Dreiecken und gleichseitigen Dreiecken sein.
Es ist jedoch zumindest im zweidimensionalen Fall auch mit Matrizen (Translationsmatrixen, Spiegelmatrixen und Drehmatrixen) und Vektoren für die Strecken, die die Iterationen definieren, möglich. Die Addition oder Multiplikation dieser 2x2-Matrizen erfolgt dann iterativ, sodass die Koordinaten der Teilstrecken gegen einen bestimmten Grenzwert konvergieren. Jedes Element des Einheitsintervalls, zum Beispiel 0,625, wird dann auf diesen Grenzwert abgebildet.
Dreidimensionale „Koch-Kurve“[Bearbeiten | Quelltext bearbeiten]
Die Koch-Kurve kann auf 3 Dimensionen verallgemeinert werden. Die Startfigur ist ein regelmäßiges Tetraeder. Bei jedem Iterationsschritt werden die gleichseitigen Dreiecke der Oberfläche in 4 kongruente Dreiecke mit halber Seitenlänge aufgeteilt und jeweils ein regelmäßiges Tetraeder auf das mittlere dieser Dreiecke gesetzt. Die Kantenlänge der hinzugefügten Tetraeder halbiert sich also mit jedem Iterationsschritt.
Dieses dreidimensionale Fraktal nähert sich mit jedem Iterationsschritt dem umbeschriebenen Würfel an, dessen alternierende Ecken die 4 Ecken des ursprünglichen Tetraeders sind. Nach dem ersten Schritt entsteht ein Sterntetraeder. Die Seitenflächen aller Tetraeder sind parallel zu einer Seitenfläche des ursprünglichen Tetraeders. Die Ecken aller Tetraeder sind Gitterpunkte eines Kubusgitters. Mit jedem Schritt verfeinert sich das Kubusgitter um den Faktor 2.




Berechnungen[Bearbeiten | Quelltext bearbeiten]
Ist die Kantenlänge des ursprünglichen regelmäßigen Tetraeders, dann ist die Kantenlänge des umbeschriebenen Würfels. Das Volumen des ursprünglichen Tetraeders beträgt und das Volumen der Teil-Tetraeder, die beim Iterationsschritt hinzugefügt werden, beträgt jeweils . Beim Iterationsschritt kommen Teil-Tetraeder hinzu und es sind insgesamt Teil-Tetraeder auf der Oberfläche dieses dreidimensionalen Fraktals sichtbar. Bei 10 realisierten Iterationsschritten würde dies zu folgenden insgesamten Anzahlen der Teil-Tetraeder führen.
Im Inneren des Fraktals entstehen Hohlräume, die die Form eines Oktaeders haben und deren Kantenlänge sich mit jedem Iterationsschritt halbiert.
Mit jedem Iterationsschritt versechsfacht sich die Anzahl der hinzugefügten Tetraeder, während das Volumen um den Faktor kleiner wird. Das Volumen der hinzugefügten Tetraeder wird also mit jedem Schritt um den Faktor kleiner, beträgt nach dem Iterationsschritt also . Das gesamte Volumen der dreidimensionalen „Koch-Kurve“ kann mithilfe der geometrischen Reihe berechnet werden und beträgt
Wegen ist das gleich dem Volumen des umbeschriebenen Würfels.
Programmierung[Bearbeiten | Quelltext bearbeiten]
Die kochsche Schneeflocke lässt sich rekursiv auf einfache Weise implementieren. Das folgende Beispiel zeigt eine Implementierung in der Programmiersprache C#.[7]
using System.Windows.Forms;
public class MainForm : System.Windows.Forms.Form
{
private Graphics graphics;
public MainForm()
{
InitializeComponent();
Text = "Koch-Kurve";
Width = 800;
Height = 600;
graphics = CreateGraphics(); // Erzeugt ein Grafikobjekt für das Zeichnen auf dem Hauptfenster.
Paint += OnPaint; // Verknüpft die Ereignisbehandlungsmethode mit dem Paint Ereignis des Hauptfensters.
}
private void OnPaint(object sender, PaintEventArgs e)
{
float faktor = (float) Math.Sqrt(3) / 2; // Skalierungsfaktor für die Höhe der gleichseitigen Dreiecke
float x1 = 200, y1 = 200, x2 = 600, y2 = 200;
// Definiert eine Farbe mit RGB-Werten.
Color farbe = Color.FromArgb(0, 0, 255);
// 3 Aufrufe der Methode mit maximaler Rekursionstiefe 4. Die kochsche Schneeflocke besteht aus 3 Koch-Kurven.
ZeichneKochKurve(x1, y1, x2, y2, Color.FromArgb(0, 0, 0), 0, 4);
ZeichneKochKurve(x2, y2, (x1 + x2) / 2 + faktor * (y1 - y2), (y1 + y2) / 2 + faktor * (x2 - x1), Color.FromArgb(0, 0, 0), 0, 4);
ZeichneKochKurve((x1 + x2) / 2 + faktor * (y1 - y2), (y1 + y2) / 2 + faktor * (x2 - x1), x1, y1, Color.FromArgb(0, 0, 0), 0, 4);
}
// Diese Methode wird aufgerufen, wenn das Hauptfenster gezeichnet wird. Sie enthält 4 rekursive Aufrufe.
private void ZeichneKochKurve(float x1, float y1, float x2, float y2, Color farbe, int tiefe, int maximaleTiefe)
{
// Wenn maximale Rekursionstiefe erreicht, dann Koordinaten setzen und Strecke zeichnen
if (tiefe == maximaleTiefe)
{
graphics.DrawLine(new Pen(farbe), x1, y1, x2, y2); // Zeichnet die Strecke mit den gesetzten Koordinaten und der als Parameter angegebenen Farbe.
}
// sonst Methode für jede der 4 Teilstrecken rekursiv aufrufen
else
{
float faktor = (float) Math.Sqrt(3) / 2; // Skalierungsfaktor für die Höhe der gleichseitigen Dreiecke
// Rekursive Aufrufe der Methode für das Zerlegen der aktuellen Strecke in 4 Teilstrecken mit 1/3 der Breite und Höhe.
ZeichneKochKurve(x1, y1, (2 * x1 + x2) / 3, (2 * y1 + y2) / 3, farbe, tiefe + 1, maximaleTiefe);
ZeichneKochKurve((2 * x1 + x2) / 3, (2 * y1 + y2) / 3, (x1 + x2) / 2 + faktor * (y2 - y1) / 3, (y1 + y2) / 2 + faktor * (x1 - x2) / 3, farbe, tiefe + 1, maximaleTiefe);
ZeichneKochKurve((x1 + x2) / 2 + faktor * (y2 - y1) / 3, (y1 + y2) / 2 + faktor * (x1 - x2) / 3, (x1 + 2 * x2) / 3, (y1 + 2 * y2) / 3, farbe, tiefe + 1, maximaleTiefe);
ZeichneKochKurve((x1 + 2 * x2) / 3, (y1 + 2 * y2) / 3, x2, y2, farbe, tiefe + 1, maximaleTiefe);
}
}
}
Erstveröffentlichungen[Bearbeiten | Quelltext bearbeiten]
- Helge von Koch: Une courbe continue sans tangente, obtenue par une construction géometrique élémentaire. In: Arkiv för Matematik. Band 1, 1904, S. 681–704.
- Helge von Koch: Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes planes. In: Acta Mathematica. Band 30, 1906, S. 145–174.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- John J. O’Connor, Edmund F. Robertson: Niels Fabian Helge von Koch. In: MacTutor History of Mathematics archive (englisch).
- Eric W. Weisstein: Koch Snowflake. In: MathWorld (englisch).
- Tetraederfraktal (T-Fraktal) Mathematische Modelle, TU Dresden
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Stack Exchange Inc.: Area of Generalized Koch Snowflake
- ↑ Eric Baird: The Koch curve in three dimensions. scrolle zu 2. The “Classic” Koch curve. ResearchGate, Mai 2014, S. 1, abgerufen am 17. November 2020 (englisch).
- ↑ Eric Baird: The Koch curve in three dimensions. scrolle zu 4.The Koch “leaf”. ResearchGate, Mai 2014, S. 2, abgerufen am 17. November 2020 (englisch).
- ↑ Go Figure: Koch Snowflake Area
- ↑ Eric Baird: The Koch curve in three dimensions. scrolle zu 3. Generalising the Koch Curve. ResearchGate, Mai 2014, S. 2, abgerufen am 17. November 2020 (englisch).
- ↑ Stack Exchange Inc.: Area fractal pentagrams
- ↑ Rosetta Code: Koch curve

































![{\displaystyle f_{n}\colon [0,1]\to {\mathbb {R} }^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e140c9bb26a5999a48febfbe79bdd7002f41baec)

![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)


























![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


![{\displaystyle [0{,}101]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0199441d0a24a5b87981bf752286a3d495264a76)










