Goldener Schnitt

Der Goldene Schnitt (lateinisch sectio aurea „Goldener Schnitt“, proportio divina „göttliche Proportion“), gelegentlich auch stetige Teilung einer Strecke, ist ihre Zerlegung in zwei Teilstrecken in der Weise, dass sich die längere Teilstrecke zur kürzeren Teilstrecke verhält wie die Gesamtstrecke zur längeren Teilstrecke. Das Konzept ist bereits seit der Antike zur Zeit des Euklid bekannt. Der Goldene Schnitt findet häufige Anwendung in der Kunst, taucht aber auch in der Natur auf.
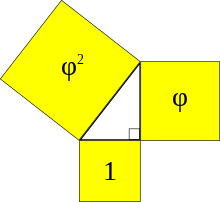
In mathematischen Formeln ausgedrückt, gilt für den Goldenen Schnitt zweier Teilstrecken und (siehe Bild):
- oder .
Das mittels Division dieser Größen als Zahl berechnete Teilungsverhältnis des Goldenen Schnittes ist eine dimensionslose, irrationale Zahl, das heißt eine Zahl, die sich nicht als Bruch ganzer Zahlen darstellen lässt. Die Folge ihrer Nachkommastellen zeigt daher auch kein periodisches Muster. Diese Zahl wird ebenfalls als Goldener Schnitt bezeichnet. Als mathematisches Symbol für den Goldenen Schnitt wird meist der griechische Buchstabe Phi (, oder , heutige Aussprache [fi:]), seltener auch Tau (, ) oder verwendet. Es gilt
- , wobei die Quadratwurzel aus 5 bezeichnet. Seit 2021 sind 10 Billionen Dezimalstellen des Goldenen Schnittes bekannt.
Aus Sicht der Mathematik besitzt der Goldene Schnitt zahlreiche besondere Eigenschaften. Neben der geometrischen Auffassung kann er auch als die positive Lösung der quadratischen Gleichung definiert werden. Er ist damit eine algebraische Zahl vom Grade 2. Bemerkenswert ist seine enge Verbindung zu der Fibonacci-Folge, die sich durch die explizite Binet-Formel ausdrückt, obgleich die Fibonacci-Folge zunächst nur rekursiv, also implizit erklärt ist. Darüber hinaus konnte gezeigt werden, dass der Goldene Schnitt unter den irrationalen Zahlen (bis auf eine gewisse Form der Äquivalenz) am schlechtesten durch Brüche angenähert werden kann. Zentrales Argument für diese Tatsache ist seine Kettenbruchentwicklung, die nur aus der Zahl 1 besteht, ergo unter allen Kettenbrüchen am langsamsten konvergiert.
Der Goldene Schnitt ist in der mathematischen Literatur seit der Zeit der griechischen Antike (Euklid von Alexandria) nachgewiesen, war jedoch vor mehr als 2300 Jahren nur Wenigen bekannt. Vereinzelt schon im Spätmittelalter und besonders dann in der Renaissance, etwa durch Luca Pacioli und Johannes Kepler, wurde er auch in philosophische und theologische Zusammenhänge gestellt. Der Überlieferung nach erhielt er mit diesem Namen erst ab der ersten Hälfte des 19. Jahrhunderts größeren Bekanntheitsgrad. Die heute gebräuchliche Bezeichnung bzw. für den Zahlenwert geht auf den amerikanischen Mathematiker Mark Barr zurück, der sie um das Jahr 1909 herum einführte. Einigen bedeutenden Künstlern, wie Leonardo da Vinci, Friedrich Hölderlin oder Béla Bartók, wurde nachgesagt, den Goldenen Schnitt gezielt bei manchen ihrer Werke eingesetzt zu haben, jedoch gelten solche Aussagen als umstritten. Der Goldene Schnitt ist nicht nur in Mathematik, Kunst oder Architektur von Bedeutung, sondern findet sich auch in der Natur, beispielsweise bei der Anordnung von Blättern und in Blütenständen mancher Pflanzen wieder.
Definition[Bearbeiten | Quelltext bearbeiten]
Man sagt, dass zwei Größen im Verhältnis des Goldenen Schnittes stehen, falls
erfüllt ist. Die Zahl
wird dann ebenfalls Goldener Schnitt genannt. Es muss sich bei den Werten und dabei nicht um (dimensionslose) reelle Zahlen handeln; auch eine Assoziation zu physikalischen Größen unter Zuweisung entsprechender Maßeinheiten ist möglich. Klassisch ist dabei die Veranschaulichung über das Teilungsverhältnis zweier Strecken (bei dem die längere Strecke als „Major“ und die kürzere als „Minor“ bezeichnet wird[1]), aber auch andere Einheiten können betrachtet werden, siehe zum Beispiel Goldenes Rechteck.
In der Literatur wird der Ausdruck „Goldener Schnitt“ jedoch auch für andere Dinge verwendet. Er bezeichnet[2]
- den Vorgang der Teilung an sich,
- gelegentlich den Teilungspunkt,
- meist jedoch die Zahl selbst.
Bestimmung des Verhältnisses[Bearbeiten | Quelltext bearbeiten]

Es bezeichnen die Teilstreckenlängen der Gesamtstrecke . Es gilt dann nach Definition des Goldenen Schnitts die Relation[3]
- .
- Multipliziere mit :
a) Lösung der quadratischen Gleichung mittels Lösungsformel:
- .
- Nur die positive Lösung ist hier von Bedeutung:
- .
- Damit ist
- .
b) Graphische Lösung der quadratischen Gleichung[4]

- .
- Setzt man , ergibt sich die quadratische Gleichung
- ,
- mit und .
- Deren Lösung gelingt beispielsweise mit der im Folgenden beschriebenen Konstruktion in einem kartesischen Koordinatensystem.
- Nach dem Ziehen des Kreises mit Radius gleich um den Mittelpunkt und dem anschließenden Festlegen der zueinander parallelen Tangenten an den Punkten und , werden auf den entsprechenden Tangenten, wegen und ,[4] die Punkte und bestimmt. Eine Verbindung des Punktes mit erzeugt auf dem Kreisbogen die Schnittpunkte und . Die beiden abschließenden geraden Linien ab Punkt durch und liefern auf der -Achse die Punkte und mit den Längen und .[4]
- Der hier relevante positive Wert der Lösung: .
Geschichte[Bearbeiten | Quelltext bearbeiten]
Antike[Bearbeiten | Quelltext bearbeiten]
Die erste erhalten gebliebene genaue Beschreibung des Goldenen Schnittes findet sich im zweiten Buch der Elemente des Euklid (um 300 v. Chr., siehe Innere Teilung nach Euklid), der darauf über seine Untersuchungen an den platonischen Körpern und dem Fünfeck beziehungsweise dem Pentagramm stieß. Seine Bezeichnung für dieses Teilungsverhältnis wurde später ins Lateinische als „proportio habens medium et duo extrema“ übersetzt, was als „Teilung im inneren und äußeren Verhältnis“ bezeichnet wird.[5][6]
Mittelalter[Bearbeiten | Quelltext bearbeiten]

In seinem Rechenbuch Liber abbaci (nicht erhaltene Erstfassung 1202, erhaltene 2. Fassung nicht vor 1220), einem umfangreichen arithmetischen und algebraischen Lehrwerk über das Rechnen mit den indo-arabischen Ziffern, kommt der italienische Mathematiker Leonardo da Pisa, genannt „Fibonacci“, kurz auf die später nach ihm benannte Fibonacci-Folge zu sprechen.[7] Fibonacci führt die Zahlenfolge vor (2, 3, 5, 8 … bis 377) und weist darauf hin, dass sich jedes Glied der Reihe (ab dem dritten) durch Summierung der beiden vorhergehenden Reihenglieder errechnen lässt. Eine weitere Beschäftigung mit dieser Folge findet sich bei ihm nicht, das heißt der Zusammenhang zum Goldenen Schnitt wird von ihm nicht dargestellt. Dass ihm allerdings der (erst später so genannte) Goldene Schnitt bekannt und in der Tradition Euklids ein Begriff war, zeigt sich gegen Ende seines Werks bei einer algebraischen Aufgabe, in der es (in moderner Formulierung wiedergegeben) darum geht[8] und zu finden mit und . Hierzu weist Fibonacci darauf hin, dass im Fall von die Proportion gilt, 10 also von und im Verhältnis des Goldenen Schnittes geteilt wird („et scis, secundum hanc diuisionem, 10 diuisa esse media et extrema proportione; quia est sicut 10 ad maiorem partem, ita maior pars ad minorem“).[9] Aber auch hier stellt er den Zusammenhang zum Goldenen Schnitt nicht her.
Renaissance[Bearbeiten | Quelltext bearbeiten]

Die Entdeckung, dass sich bei Teilung eines Gliedes der Fibonacci-Folge durch das vorhergehende Reihenglied als Näherungswert ergibt, wurde lange Zeit Johannes Kepler zugeschrieben, konnte jedoch Ende des 20. Jahrhunderts schon in einer handschriftlichen Anmerkung nachgewiesen werden, mit der ein mutmaßlich aus Italien stammender Leser in der ersten Hälfte des 16. Jahrhunderts Euklids Theorem II.11 in der Euklid-Ausgabe Paciolis von 1509 kommentierte:
“Sit linea ab 233 pedum, divisa ut docet 11 huius in duo inaequalia in puncto h et sit bh portio eius maior 144 et ha portio eius minor 89. ducatur ab in ha et perveniunt 20737 et bh in se et perveniunt 20736. et sic cognosces quod in mutationibus non est laborandum quid impossibile est numerum ita dividi ut ista 11 proponit. similiter accidit si linea 13 pedum dividatur in lineam 8 pedum, et lineam 5.”
„Eine Gerade ab von 233 Fuß sei so, wie es Theorem 11 hier vorführt, an einem Punkt h in zwei ungleiche Teile geteilt, und dabei sei bh sein größerer Teil mit 144 und ha sein kleinerer Teil mit 89. ab sei multipliziert mit ha, und es ergeben sich 20737, und bh multipliziert mit sich selbst, so ergeben sich 20736. Und daran magst du erkennen, dass man sich nicht mit Ersetzungen abzumühen braucht, um zu zeigen, dass es unmöglich ist, die Zahl so zu teilen, wie es hier Theorem 11 vorführt. Das gleiche ergibt sich, wenn eine Gerade von 13 Fuß in eine Gerade von 8 und eine von 5 Fuß geteilt wird.“[10]
Der Herausgeber dieser Euklid-Ausgabe, der Franziskaner Luca Pacioli di Borgo San Sepolcro (1445–1514), der an der Universität Perugia Mathematik lehrte, hatte sich intensiv mit dem Goldenen Schnitt befasst. Er nannte diese Streckenteilung „vermutlich als erster […] divina proportio (göttliches Verhältnis)“,[11] was sich auf Platons Identifizierung der Schöpfung mit den fünf platonischen Körpern bezog, zu deren Konstruktion der Goldene Schnitt ein wichtiges Hilfsmittel darstellt. Sein gleichnamiges Werk De divina proportione von 1509 besteht aus drei unabhängigen Büchern. Bei dem ersten handelt es sich um eine rein mathematische Abhandlung, die jedoch keinerlei Bezug zur Kunst und Architektur herstellt. Das zweite ist ein kurzer Traktat über die Schriften des Römers Vitruv aus dem 1. Jahrhundert v. Chr. zur Architektur, in denen Vitruv die Proportionen des menschlichen Körpers als Vorlage für Architektur darstellt. Dieses Buch enthält eine Studie von Leonardo da Vinci (1452–1519) über den vitruvianischen Menschen. Das Verhältnis der Seitenlänge des den Menschen umgebenden Quadrats zum Radius des umgebenden Kreises – nicht das Verhältnis der Proportionen des Menschen selbst – in diesem berühmten Bild entspricht mit einer Abweichung von 1,7 % dem Goldenen Schnitt, der jedoch im zugehörigen Buch gar nicht erwähnt wird. Darüber hinaus würde diese Abweichung bei einem konstruktiven Verfahren nicht zu erwarten sein.
Im Oktober 1597 stellte Johannes Kepler in einem Brief an seinen früheren Tübinger Professor Michael Maestlin die Frage, warum es nur eine einzige mögliche Lösung für die Aufgabe gebe, ein rechtwinkliges Dreieck zu konstruieren, bei dem das Verhältnis der kürzeren zur längeren Seite dem der längeren zur Hypotenuse entspricht (Kepler-Dreieck). Auf das Original dieses Briefes notierte Maestlin eine Berechnung, die die Hypotenuse einmal mit 10 und einmal mit 10.000.000, und für den letzteren Fall dann die längere Seite mit 7.861.514 und die kürzeste Seite mit 6.180.340 beziffert. Das entspricht einer bis auf die sechste Nachkommastelle genauen (und bis zur fünften korrekten) Angabe des Goldenen Schnittes und ist nach den älteren sexagesimalen Berechnungen der Antike die erste bekannte dezimale Angabe dieser Art.[12]
Seit dem 18. Jahrhundert[Bearbeiten | Quelltext bearbeiten]
Populär wurde der Begriff Goldener Schnitt erst in der ersten Hälfte des 19. Jahrhunderts, obwohl die mathematischen Prinzipien schon seit der Antike bekannt waren. Der Begriff Goldene Zahl stammt aus dieser Zeit, noch 1819 wird dieser Begriff mit dem Meton-Zyklus in einem der griechischen Kalendersysteme in Verbindung gebracht.[13] In der deutschen Literatur sind bereits Anfang des 18. Jahrhunderts vereinzelt Hinweise auf eine sinngemäße bzw. wortwörtliche Form des Begriffes „Goldener Schnitt“ zu finden. Erst ab dem zweiten Viertel des 19. Jahrhunderts war er weiter verbreitet.[14] Die folgenden Beispiele aus der deutschen Literatur verweisen auf den Begriff in ähnlicher Art und Weise.
1717 wurde der Begriff Goldener Schnitt sinngemäß von M. Johann Wentzel Kaschube in seinem Werk Cursus mathematicus …[15] verwendet. Er beschreibt darin eine geometrische Aufgabe (Näheres im Abschnitt Konstruktionsverfahren), deren Lösung dieses besondere Teilungsverhältnis verlangt. Am Schluss der Aufgabe §.35. ist zu lesen: „Die Alten hissen [sc. hießen] diesen Schnitt den Goldenen.“[16] Zu jener Zeit fand das Teilungsverhältnis des Goldenen Schnittes auch in der Akustik im Zusammenhang mit Verhältnissen der Saitenlänge Anwendung. Diese Form der Saitenteilung – so Ernst Florens Friedrich Chladni 1802 in Die Akustik unter Die geometrische Theilung[17] – wollte auch Gottfried Wilhelm Leibniz.[18] Zwar lassen sich damit nicht Tonhöhenabstände, sprich Intervalle finden, „desto brauchbarer ist sie aber, wie im folgenden Abschnitte wird gezeigt werden, zu gewissen nothwendigen Abänderungen derselben.“[17] Chladni leitete die Tonverhältnisse also nicht aus den Saitenlängen ab, sondern aus den Verhältnissen der Schwingungszahlen.[17] Bezüglich des Goldenen Schnitts merkt Chladni an: „Es ist diese Theilung eben dasselbe, was von einigen ältern Mathematikern, die besondere Eigenschaften darin finden wollten, sectio aurea, oder sectio divina [der Goldene Schnitt oder göttliche Schnitt] genennt worden ist.“[17]
Etwas mehr als fünfzig Jahre später wurden die Proportionen des menschlichen Körpers wissenschaftlich mit denen des Goldenen Schnittes verglichen. Adolf Zeising benennt 1854 in Neue Lehre von den Proportionen des menschlichen Körpers … das Ergebnis der „Maassbestimmungen […] kurzweg, das Proportionalgesetz“. Er beschreibt es als einen geometrischen Weg zur proportionalen Teilung einer Linie [19] und stellt fest:
„Die Mathematiker nennen die hier erörterte Theilung einer gegebenen Linie die ‚Theilung im äussern und mittlern Verhältnisse‘ oder ‚den goldnen Schnitt‘. Der Grund der letztern Benennung ist mir nicht bekannt; doch rührt sie wahrscheinlich daher, weil man die ausserordentlichen Vorzüge des Verhältnisses, welches man durch diese Theilung gewinnt, und die Vollkommenheit der durch dieses Verhältniss gebildeten Proportion mit richtigem Blicke erkannt hat.“
Gustav Theodor Fechner, ein Begründer der experimentellen Psychologie, stellte 1876 bei Untersuchungen mit Versuchspersonen anhand von Rechtecken in der Tat eine Präferenz für den Goldenen Schnitt fest.[21] Die Ergebnisse bei der Streckenteilung und bei Ellipsen fielen jedoch anders aus. Neuzeitliche Untersuchungen zeigen, dass das Ergebnis solcher Experimente stark vom Kontext der Darbietung abhängt. Fechner fand ferner bei Vermessungen von Bildern in verschiedenen Museen Europas, dass die Seitenverhältnisse im Hochformat im Mittel etwa 4:5 und im Querformat etwa 4:3 betragen und sich damit deutlich vom Goldenen Schnitt unterscheiden.[22][23]
Bis ins späte 20. Jahrhundert erhielt der Goldene Schnitt auf viele Art und Weise seine Aufmerksamkeit ausschließlich in der Makrowelt. Dann aber entdeckten Wissenschaftler bei Forschungen in der atomaren Welt überraschenderweise Gebilde mit mathematischen Kennwerten, die dem Goldenen Schnitt gleichen. Die Forschungsergebnisse der beiden folgenden Beispiele fanden in den betreffenden Wissenschaftsbereichen hohe internationale Anerkennung.
Als Erster erkannte Dan Shechtman mit seinen Kollegen 1982 bei Röntgenstrukturanalysen Beugungsbilder mit fünfzähliger Symmetrie in Quasikristallen[24] der Festkörperphysik. Für diese Entdeckung bekam Shechtman 2011 den Nobelpreis für Chemie. Näheres ist im Abschnitt Quasikristalle enthalten. Die erstmalige Entdeckung des Goldenen Schnitts in fester Materie gelang Forschern des Helmholtz-Zentrums Berlin für Materialien und Energie (HZB) im Kristall aus Kobalt-Niobat (veröffentlicht in der Zeitschrift Science, Januar 2010).[25] Näheres ist im Abschnitt Kobalt-Niobat enthalten.
Grundlegende mathematische Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Irrationalität und Algebraizität[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt ist eine irrationale Zahl; das heißt, er lässt sich nicht als Bruch zweier ganzer Zahlen darstellen.[26] Weiter bedeutet es, dass die Dezimalentwicklung kein periodisches Muster aufzeigt. Die ersten 50 Nachkommastellen des Goldenen Schnittes sind gegeben durch
- .[27]
Seit dem 14. Februar 2021 sind 10 Billionen (10 × 1012) Nachkommastellen von berechnet und verifiziert worden. Zudem gelten bereits 20 Billionen Stellen als berechnet, jedoch noch nicht als verifiziert.[28]
Der Grund, warum irrational ist, verbirgt sich hinter der Irrationalität von .
Der Beweis, dass irrational sein muss, erfolgt analog zum Beweis der Irrationalität der Wurzel aus 2 bei Euklid. Dazu ist es nützlich, das Gesetz der bis auf die Reihenfolge eindeutigen Zerlegbarkeit natürlicher Zahlen in Primzahlen zu kennen. Nimmt man an, es sei mit einem vollständig gekürzten Bruch mit positiven ganzen Zahlen , so gilt bereits
- .
Es ist also und ergo auch durch teilbar, da eine Primzahl ist. Damit besitzt also den Primteiler ,und dieser taucht bei in gerader Anzahl auf, da sich beim Quadrieren alle Primfaktoren verdoppeln. Da und teilerfremd sind – es ist nach Annahme vollständig gekürzt – taucht der Primfaktor nirgends in auf. Ergo taucht er nur einmal in auf. Dies ist ein Widerspruch zur eindeutigen Primfaktorzerlegung, die besagt, dass auf beiden Seiten gleich viele Fünfen auftauchen müssen, aber ist keine gerade Zahl.[29] Zu guter Letzt muss dann auch irrational sein, da irrationale Zahlen im Produkt mit rationalen Zahlen (außer 0) und in Summe mit rationalen Zahlen wieder irrational sind.
Die Goldene Zahl ist ferner eine algebraische Zahl vom Grad 2, insbesondere kann sie mit Zirkel und Lineal konstruiert werden. Damit grenzt sie sich von anderen berühmten Konstanten, wie der Kreiszahl oder der Eulerschen Zahl , ab, die transzendent, und damit niemals Nullstelle eines nicht-konstanten Polynoms mit rationalen Koeffizienten sind.
Zusammenhang mit den Fibonacci- und Lucas-Zahlen[Bearbeiten | Quelltext bearbeiten]
| Abweichung zu in % | |||
|---|---|---|---|
| 1 | 1 | = 1,0000 | −38 |
| 1 | 2 | = 2,0000 | +23 |
| 2 | 3 | = 1,5000 | −7,3 |
| 3 | 5 | ≈ 1,6667 | +3,0 |
| 5 | 8 | = 1,6000 | −1,1 |
| 8 | 13 | = 1,6250 | +0,43 |
| 13 | 21 | ≈ 1,6154 | −0,16 |
| 21 | 34 | ≈ 1,6190 | +0,063 |
| 34 | 55 | ≈ 1,6176 | −0,024 |
| 55 | 89 | ≈ 1,6182 | +0,0091 |
| 89 | 144 | ≈ 1,6180 | −0,0035 |
| 144 | 233 | ≈ 1,6181 | +0,0013 |
In einem engen Zusammenhang zum Goldenen Schnitt steht die unendliche Zahlenfolge der Fibonacci-Zahlen (siehe unten die Abschnitte Mittelalter und Renaissance):
- .
Die jeweils nächste Zahl in dieser Folge wird als Summe der beiden vorangehenden erhalten. Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Folge strebt gegen den Goldenen Schnitt (siehe Tabelle). Das rekursive Bildungsgesetz bedeutet nämlich
- .
Sofern dieses Verhältnis gegen einen Grenzwert konvergiert, muss für diesen gelten
- .
In der Tat lässt sich daraus
folgern.[30] Die Glieder der Fibonacci-Folge lassen sich für alle über die Formel von Binet berechnen:[31]
- .
Diese Formel liefert die für die Fibonacci-Folge veranschlagten Anfangswerte und und erfüllt die rekursive Gleichung für alle mit .[32]
Ähnlich gilt
für die -te Lucas-Zahl.[33] Allgemeiner ist jede komplexe Folge mit von der Form , wobei komplexe Zahlen sind, und umgekehrt.[34]
Kettenbruchentwicklung[Bearbeiten | Quelltext bearbeiten]
Da der Goldene Schnitt irrational ist, stellt sich die Frage, wie gut er sich durch rationale Zahlen annähern lässt. Grundsätzlich konnte gezeigt werden, dass es für eine beliebige irrationale Zahl stets unendlich viele rationale Zahlen gibt, so dass
- .
Dieses Resultat ist fundamental im Gebiet der diophantischen Approximation.[35] Erhöht sich der Nenner , sind grundsätzlich auch bessere Annäherungen möglich, wie das sogar quadratische Abklingen der rechten Seite zeigt. Bemerkenswert ist die Konstante , die optimal gewählt ist, also nicht weiter vergrößert werden kann. Grund dafür ist der Goldene Schnitt, der (zusammen mit zu ihm äquivalenten Zahlen) die Eigenschaft hat, dass für alle nur endlich viele rationale Annäherungen mit
existieren.[36] Für irrationale Zahlen, die nicht zu äquivalent sind, lässt sich die Konstante größer als wählen (nämlich mit Wert (Satz von Hurwitz)). Der Goldene Schnitt gehört also unter den irrationalen Zahlen zu den am schlechtesten durch rationale Zahlen approximierbaren. Da seine Kettenbruchentwicklung überdies nur Einsen enthält, ist er in diesem Sinn die „irrationalste aller Zahlen“.[37][38][39]
Der mathematische Beweis der oberen Aussage fußt auf sogenannten Kettenbrüchen. Jede reelle Zahl lässt sich (im Wesentlichen eindeutig) durch einen Kettenbruch darstellen. Bricht man diesen nach endlich vielen Schritten ab, ergibt sich eine „besonders gute“ rationale Annäherung an diese Zahl. Für die Goldene Zahl gilt nun aber , woraus sich durch wiederholte Anwendung ergibt:
- .
Bricht man die Kettenbruchentwicklung ab, erhält man stets einen Bruch aus zwei aufeinanderfolgenden Fibonacci-Zahlen.[40] Weil im Kettenbruch lediglich Einsen auftauchen – die kleinste natürliche Zahl –, nähert sich dieser Kettenbruch mit der „minimal möglichen Geschwindigkeit“ der Goldenen Zahl an. Im Vergleich ist der Kettenbruch zur Kreiszahl – ebenfalls irrational – deutlich schneller konvergent.
In der Theorie der dynamischen Systeme werden Zahlen, deren unendliche Kettenbruchdarstellung ab einer Stelle nur noch Einsen enthält, als „noble Zahlen“ bezeichnet. In diesem Kontext wird der Goldene Schnitt als „nobelste“ aller noblen Zahlen bezeichnet.[41]
Geometrische Aussagen[Bearbeiten | Quelltext bearbeiten]
Konstruktionsverfahren[Bearbeiten | Quelltext bearbeiten]
Als Konstruktionsverfahren werden nach den Postulaten des Euklid nur diejenigen Verfahren akzeptiert, die sich auf die Verwendung von Zirkel und Lineal (ohne Skala) beschränken. Für die Teilung einer Strecke im Verhältnis des Goldenen Schnittes gibt es eine Fülle derartiger Verfahren, von denen im Folgenden exemplarisch nur einige erwähnt werden. Unterschieden wird dabei eine innere und äußere Teilung. Bei der äußeren Teilung wird der in der Verlängerung der Ausgangsstrecke außen liegende Punkt gesucht, der die vorhandene Strecke zum (größeren) Teil des Goldenen Schnittes macht. Der Goldene Schnitt stellt dabei einen Spezialfall der harmonischen Teilung dar. Aufgeführt werden im Folgenden auch zwei moderne, von Künstlern gefundene Konstruktionen.
Innere Teilung[Bearbeiten | Quelltext bearbeiten]
 |
Klassisches Verfahren mit innerer Teilung nach Heron von Alexandria, das wegen seiner Einfachheit beliebt ist:[42]
Dies kann wie folgt eingesehen werden: Über den Satz des Pythagoras ergibt sich für die Länge der Hypotenuse der Wert
Subtrahiert man von dieser die Länge |DC|AB, verbleibt gerade AD|AB||AB||AS|. Aus den algebraischen Vorüberlegungen ist nun bekannt, dass dies das Verhältnis der stetigen Teilung ist.[43] |

|
Innere Teilung nach Euklid:
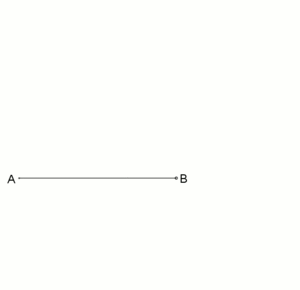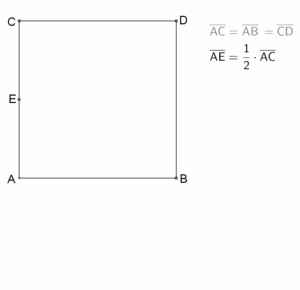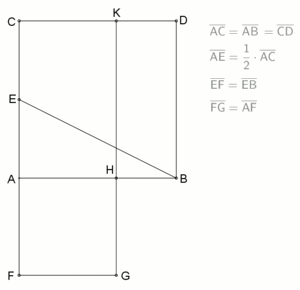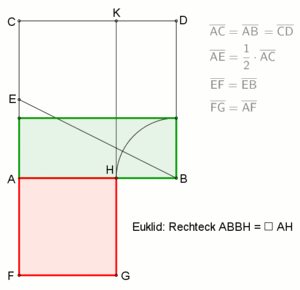 Johann Friedrich Lorenz beschrieb im Jahr 1781 in seinem Buch Euklids Elemente folgende Aufgabenstellung von Euklid: „Eine gegebne gerade Linie, AB, so zu schneiden, daß das Rectangel aus der Ganzen und Einem der Abschnitte, dem Quadrat des anderen Abschnitts gleich sey.“[44] Das Ergebnis der nebenstehenden Animation zeigt, die Strecke AB ist in einem Verhältnis geteilt, das als Goldener Schnitt mit innerer Teilung bezeichnet wird. Als Darstellung dieses Verfahrens hat sich eine vereinfachte Konstruktion, siehe linkes Bild, bewährt:
|
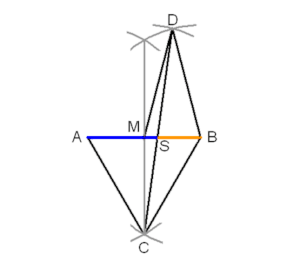
|
Konstruktion nach dem österreichischen Künstler Kurt Hofstetter, die dieser 2005 im Forum Geometricorum[45] publizierte:
|
Äußere Teilung[Bearbeiten | Quelltext bearbeiten]
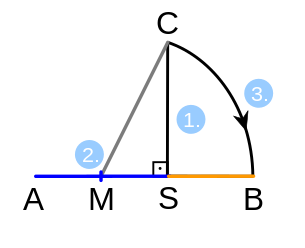
|
Klassisches Verfahren mit äußerer Teilung nach Euklid:
 „Die Seiten eines demselben Kreis einbeschriebenen gleichseitigen Sechsecks und eines gleichseitigen Zehnecks zusammen ergeben eine Strecke, die in stetiger Teilung geteilt ist, wobei die Seite des Sechsecks der größere Teil ist.“[46] Die nebenstehende Animation (am Ende mit 30 s Pause) zeigt prinzipiell die hierfür erforderlichen Konstruktionsschritte. Die abschließend eingetragenen strichlierten Linien sowie die Punkte K und L sind nicht Teil der Lösung nach Euklid. Sie sollen lediglich den konstruktiven Weg zur folgenden Vereinfachung verdeutlichen. Die Darstellung im linken Bild hat sich als vereinfachte Konstruktion bewährt:
Dieses Verfahren wird für die Konstruktion des Fünfecks bei gegebener Seitenlänge verwendet. |

|
Konstruktion nach dem amerikanischen Künstler George Odom, die dieser 1982 entdeckte:[47]
Die algebraische Herleitung ist im Unterabschnitt Im Umkreis eines gleichseitigen Dreiecks beschrieben. |
Im Fünfeck und im Pentagramm[Bearbeiten | Quelltext bearbeiten]

Regelmäßiges Fünfeck und Pentagramm bilden jeweils eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite eines regelmäßigen Fünfecks befindet sich im Goldenen Schnitt zu seinen Diagonalen. Die Diagonalen untereinander wiederum teilen sich ebenfalls im Goldenen Verhältnis, das heißt, verhält sich zu wie zu . Der Beweis dazu nutzt die Ähnlichkeit geeignet gewählter Dreiecke.[48]
Das Pentagramm, eines der ältesten magischen Symbole der Kulturgeschichte, steht in einer besonders engen Beziehung zum Goldenen Schnitt.[49] Zu jeder Strecke und Teilstrecke im Pentagramm findet sich ein Partner, der mit ihr im Verhältnis des Goldenen Schnittes steht. In der Abbildung sind alle drei möglichen Streckenpaare jeweils blau (längere Strecke) und orange (kürzere Strecke) markiert. Sie lassen sich über das oben beschriebene Verfahren der stetigen Teilung nacheinander erzeugen. Im Prinzip ist es damit in das verkleinerte Pentagramm fortsetzbar, das in das innere Fünfeck gezeichnet werden könnte, und damit in alle weiteren. Stünden die beiden Strecken in einem Verhältnis ganzer Zahlen, müsste dieses Verfahren der fortgesetzten Subtraktion irgendwann Null ergeben und damit abbrechen. Die Betrachtung des Pentagramms zeigt aber anschaulich, dass das nicht der Fall ist. Eine Weiterentwicklung dieser Geometrie findet sich bei der Penrose-Parkettierung.[50]
Für den Beweis, dass es sich um den Goldenen Schnitt handelt, beachte man, dass neben den vielen Strecken, die aus offensichtlichen Symmetriegründen gleich lang sind, auch gilt. Ursache ist, dass das Dreieck zwei gleiche Winkel besitzt, wie durch Parallelverschiebung der Strecke erkannt werden kann, und daher gleichschenklig ist. Nach dem Strahlensatz gilt:
Wird ersetzt und die Gleichheit der auftretenden Teilstücke beachtet, so wird genau die obige Definitionsgleichung für den Goldenen Schnitt erhalten.
Im gleichschenkligen Dreieck[Bearbeiten | Quelltext bearbeiten]

In einem gleichschenkligen Dreieck , dessen Grundseite längengleich zu der Höhe ist, teilt der innerhalb des Dreiecks liegende Schnittpunkt des Inkreises mit der Höhe diese im Goldenen Schnitt.
Ohne Beschränkung der Allgemeinheit kann angenommen werden. Die rechtwinkligen Dreiecke und sind kongruent, da sie in zwei Seiten und dem (rechten) Gegenwinkel der größeren Seite übereinstimmen. Es gilt und damit . Nach dem Satz des Pythagoras gilt in dem rechtwinkligen Dreieck . Ebenfalls nach dem Satz des Pythagoras gilt in dem rechtwinkligen Dreieck : . Mit folgt hieraus = (Höhe von ABC) : (Durchmesser des Inkreises von ABC), was zu zeigen war.[51]
Im Umkreis eines gleichseitigen Dreiecks[Bearbeiten | Quelltext bearbeiten]

In dem gleichseitigen Dreieck schneidet die durch und verlaufende Parallele zu den Umkreis in und . Ist , dann teilt die Strecke im Goldenen Schnitt.
Aus den Eigenschaften eines gleichseitigen Dreiecks und aus dem Strahlensatz folgen unmittelbar die Längengleichheiten
- und .
Nach dem Sehnensatz gilt:
Somit teilt die Strecke im Goldenen Schnitt.[52]
Im Quader[Bearbeiten | Quelltext bearbeiten]
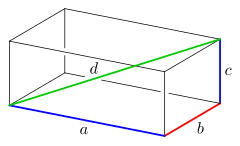
Für einen Quader mit den Kantenlängen , und , der Raumdiagonalenlänge und dem Volumen gelte , , und .
Dann gilt für den Goldenen Schnitt das Verhältnis
- .
Aus der Volumengleichung folgt wegen
- . (1)
Da die Raumdiagonale die Länge 2 hat, gilt
- . (2)
Aus (1) und (2) erhält man .
Die Lösungen mit positivem Wert sind oder und damit analog oder .
Wegen kommen nur und in Betracht.[53] Damit ergibt sich
- und
Im Ikosaeder[Bearbeiten | Quelltext bearbeiten]

Die 12 Ecken des Ikosaeders bilden die Ecken von 3 gleich großen, senkrecht aufeinanderstehenden Rechtecken mit gemeinsamem Mittelpunkt und mit den Seitenverhältnissen des Goldenen Schnittes. Die zwölf Ecken eines Ikosaeders sind also die zwölf Ecken dreier goldener Rechtecke, die paarweise aufeinander senkrecht stehen.[54] Diese Anordnung der 3 Rechtecke wird auch Goldener-Schnitt-Stuhl genannt. Weil der Ikosaeder zum Pentagondodekaeder dual ist, bilden die 12 Mittelpunkte der Fünfecke ebenfalls die Ecken eines Goldener-Schnitt-Stuhls.
Ferner kann in ein gegebenes Oktaeder ein Ikosaeder so einbeschrieben werden, dass dessen Ecken die Kanten des Oktaeders im Goldenen Schnitt teilen.[55]
Goldenes Rechteck und Goldenes Dreieck[Bearbeiten | Quelltext bearbeiten]
Ein Rechteck, dessen Seitenverhältnis dem Goldenen Schnitt entspricht, wird als Goldenes Rechteck benannt; ebenso heißt ein gleichschenkliges Dreieck, bei dem zwei Seiten in diesem Verhältnis stehen, Goldenes Dreieck.
- Zum Vergleich von Rechtecksproportionen siehe Abschnitt Vergleich mit anderen prominenten Seitenverhältnissen.
- Ein Goldenes Dreieck ist Inhalt der Methode äußere Teilung im Abschnitt Konstruktionsverfahren, äußere Teilung
Goldener Winkel[Bearbeiten | Quelltext bearbeiten]


Der Goldene Winkel wird erhalten, wenn der Vollwinkel im Goldenen Schnitt geteilt wird. Dies führt auf den überstumpfen Winkel Gewöhnlich wird aber seine Ergänzung zum Vollwinkel, als Goldener Winkel bezeichnet. Dies ist dadurch gerechtfertigt, dass Drehungen um keine Rolle spielen und das Vorzeichen nur den Drehsinn des Winkels bezeichnet.[56]
Durch wiederholte Drehung um den Goldenen Winkel entstehen immer wieder neue Positionen, etwa – wie im Bild vereinfacht dargestellt – für die Blattansätze (Näheres im Abschnitt Biologie).
Dabei zerlegen die ersten Positionen den Kreis in Ausschnitte. Diese Ausschnitte haben höchstens drei verschiedene Winkel. Im Fall einer Fibonacci-Zahl treten nur zwei Winkel auf. Für tritt der Winkel hinzu.[57]
Betrachtet man für wachsendes fortfolgend die sich verfeinernden Zerlegungen des Kreises, so teilt die -te Position stets einen der verbliebenen größten Ausschnitte, und zwar immer den im Verlauf der Teilungen zuerst entstandenen, das heißt den „ältesten“ Ausschnitt. Diese Teilung erfolgt im Goldenen Verhältnis, sodass, im Uhrzeigersinn gesehen, ein Winkel mit geradem vor einem Winkel mit ungeradem liegt.[58]
Wenn wir den Ausschnitt mit dem Winkel mit bezeichnen, so erhalten wir nacheinander die Kreiszerlegungen
,
,
,
,
,
,
,
,
,
usw.
Goldene Spirale und Spira mirabilis[Bearbeiten | Quelltext bearbeiten]
Beide Spiralen hängen mit dem Goldenen Schnitt zusammen. Sie sind nicht als Konstruktion mit Zirkel und Lineal darstellbar. Für eine Näherungskonstruktion bedarf es – wie im Folgenden erläutert – eines Goldenen Rechtecks bzw. eines Goldenen Dreiecks.[59]
Goldene Spirale[Bearbeiten | Quelltext bearbeiten]
Die Goldene Spirale, auch Bernoulli’sche Spirale genannt, ist ein Sonderfall der logarithmischen Spirale: Ihr Streckungsfaktor (siehe Zentrische Streckung) ist ,[59] die Zahl des Goldenen Schnitts. Sie lässt sich mittels rekursiver Teilung eines Goldenen Rechtecks in je ein Quadrat und ein weiteres, kleineres Goldenes Rechteck näherungsweise konstruieren. Ihr Radius ändert sich bei jeder 90°-Drehung um den Faktor .
Die Goldene Spirale lässt sich unter Verwendung von Polarkoordinaten durch
parametrisieren.[60] Die Idee von Polarkoordinaten ist hierbei, einen Punkt in der Ebene durch seinen Abstand zum Ursprung und den mit der -Achse eingeschlossen Winkel festzulegen. Dessen Polarkoordinaten sind dann , und durch Wahl des Radius in Abhängigkeit vom sich verändernden Winkel lassen sich manche geometrische Figuren durch eine entsprechende Funktion einfacher beschreiben als in klassischen kartesischen Koordinaten. Zu beachten ist, dass mehrfache Umdrehungen um den Ursprung, etwa in den Fällen (Ausgangslage), (eine Volldrehung), (zwei Volldrehungen) usw. unterschiedliche Radii hervorrufen können, was auch an der nicht-periodischen Figur der Spirale zu erkennen ist.
Eine brauchbare Näherung für die Goldene Spirale findet sich bereits bei Kepler. Man erhält diese Approximation, wenn man in die Quadrate Viertelkreise mit dem Radius der Seitenlänge des Quadrats einzeichnet. Dies ist im mittleren Bild illustriert. Im linken Bild wird die Güte dieser Approximation veranschaulicht.
-
Grün Annäherung durch Vierteilkreise (rechtes Bild); Rot Goldene Spirale; Gelb: Überlappungen.
-
Annäherung der Goldenen Spirale, unter Benutzung von Viertelkreisen und der Fibonacci-Folge
-
Goldene Spiralen sind selbstähnlich. Ihre Form wiederholt sich unendlich oft, wenn sie vergrößert wird.
Die Goldene Spirale ist unter den logarithmischen Spiralen durch die folgende Eigenschaft ausgezeichnet. Seien vier auf der Spirale aufeinanderfolgende Schnittpunkte mit einer Geraden durch das Zentrum. Dann sind die beiden Punktepaare und harmonisch konjugiert, das heißt, für ihr Doppelverhältnis gilt:[61]
Spira mirabilis[Bearbeiten | Quelltext bearbeiten]

Die Spira mirabilis ist ebenfalls ein Sonderfall der logarithmischen Spirale: Ihr Streckungsfaktor ist ,[62] sprich der Kehrwert des Goldenen Schnitts. Sie benötigt für die Näherungskonstruktion die rekursive Teilung eines Goldenen Dreiecks in je ein gleichschenkliges stumpfwinkliges Dreieck und in ein weiteres, kleineres Goldenes Dreieck. Dies ist begründet durch eine sogenannte Drehstreckung . Sie enthält eine Drehung um (entspricht ). Daraus ergibt sich eine Streckung mit dem Faktor .
Das nebenstehende Bild zeigt ein solches gleichschenkliges Dreieck mit den Basiswinkeln und dem Scheitelwinkel bei . Es gilt: .[62]
- Vorgehensweise
Es beginnt mit dem Halbieren des Winkels am Scheitel . Dabei teilt der generierte Punkt die Schenkellänge im Goldenen Schnitt. Es entsteht dabei das gleichschenklige stumpfwinklige Dreieck sowie das Dreieck . Dass letzteres auch ein Goldenes Dreieck ist, zeigt die folgende einfache Überprüfung der Winkelweiten.
Am Scheitel ergibt sich durch die Winkelhalbierende des Ausgangsdreiecks die Winkelweite ; der Basiswinkel am Scheitel bleibt unverändert . Wird die Winkelsumme eines ebenen Dreiecks mit berücksichtigt, ist am Scheitel der Basiswinkel ebenfalls . Dies zeigt auf, das entstandene Dreieck und das Goldene Dreieck sind zwei zueinander ähnliche Dreiecke.[62]
Für den Nachweis, dass der Punkt tatsächlich die Schenkellänge im Goldenen Schnitt teilt, gilt:[63]
- .
Nun bedarf es noch der Bestimmung des Polpunktes als Schnittpunkt der beiden Seitenhalbierenden und . Die darüber hinaus eingezeichneten goldenen Dreiecke und anderes mehr zeigen, dass diese Vorgehensweise beliebig weit fortgesetzt werden kann.
Mit und sind die ersten fünf Punkte auf der – noch zu konstruierenden – Spirale bestimmt. Hat der Polpunkt die Polarkoordinaten , so gilt für die Spira mirabilis die Polargleichung[62]
- .
Angenäherte Spira mirabilis mittels Kreisbögen
- Praktikable Methode als Konstruktion mit Zirkel und Lineal
An den gleichschenkligen stumpfwinkligen Dreiecken wird jeweils um deren Scheitelpunkt mit dem stumpfen Winkel, ein Kreisbogen mit der Winkelweite (entspricht ) und dem Radius gleich dem eines Schenkels gezogen.
Mit anderen Worten: Am Dreieck wird um dessen Scheitelpunkt (mit dem stumpfen Winkel), ein Kreisbogen von nach gezogen. Gleiches gilt für die weiteren ähnlichen Dreiecke.
Geometrisches Mittel[Bearbeiten | Quelltext bearbeiten]

teilt die Strecke im Verhältnis des Goldenen Schnittes:
Wird die Strecke mit Länge durch den Punkt im Verhältnis des Goldenen Schnitts in zwei Teilstrecken und mit Längen und geteilt, so ist bereits das geometrische Mittel der Zahlen und . Das folgt aus der allgemeinen Definition des geometrischen Mittels , hier: . In der Tat folgt mit bereits
- .
Des Weiteren folgt daraus unmittelbar, dass wiederum das geometrische Mittel von und ist.[64] Man hat in diesem Fall
- .
Gefalteter und verknoteter Papierstreifen[Bearbeiten | Quelltext bearbeiten]

Goldener Schnitt im gefalteten und verknoteten Papierstreifen

Symmetrisches Trapez, die gepunkteten Linien zeigen das Fünfeck im Umkreis sowie den Papierstreifen
Mit der im Folgenden beschriebenen Papierstreifen-Methode erzeugt ein sogenannter Überhandknoten[65] ein regelmäßiges Fünfeck (Bild 1), bei dem die Faltenlänge (rot) die Seitenlänge ist und die Diagonale (grün) – gebildet von der Kante des Papierstreifens – die Länge hat.
Die Diagonale und die sich daran anschließenden drei Seiten des Fünfecks bilden ein symmetrisches Trapez.[66]
Hilfssatz[Bearbeiten | Quelltext bearbeiten]
(1) Ist ein symmetrischen Trapez (Bild 2), so gilt
- ,[67]
so ist die Diagonale auch die Winkelhalbierende des Winkels .
(2) Ist der Winkel , so verhält sich
Beweise[Bearbeiten | Quelltext bearbeiten]
Zu (1)
Vorausgesetzt das Dreieck ist gleichschenklig, so ist und . Aus der Symmetrie des Trapezes ergibt sich die Gleichheit der vier betrachteten Winkel (grün).
Die beiden Diagonalen und schneiden sich im Scheitel und erzeugen damit den Scheitelwinkel .
Infolgedessen sind die Basiswinkeln des gleichschenkligen Dreiecks gleich denen des . Demzufolge ergibt sich die Gleichheit . Somit ist bestätigt: ist die Winkelhalbierende von .[68]
Zu (2)
Aufgrund der Voraussetzung folgt mittels Hilfssatz (1), der Winkel . Wegen der Symmetrie des Trapezes ist auch der Winkel . Da die Winkelsumme im Dreieck beträgt, ist auch .
Demzufolge ist das Dreieck wegen seiner Innenwinkeln ein Goldenes Dreieck. Das Dreieck hat – für eine mögliche Zahl – deshalb die Seitenlängen . Somit ist bestätigt:
- .[68]
Vorbereitung des Papierstreifens[Bearbeiten | Quelltext bearbeiten]

Papierstreifen mit den vier eingezeichneten Trapezen
Zuerst ist die Streifenbreite gleich der Trapezhöhe zu ermitteln und anschließend die Anordnung der vier Trapeze () darzustellen (Bild 3). Hierzu werden die ermittelten Abmaße des symmetrischen Trapezes – z. B. aus einem bereits konstruierten Fünfeck (siehe Bild 2) – auf einem Blatt Papier übertragen. Nach dem Beschriften der beiden Enden mit , bedarf es nur noch des Ausschneidens des Papierstreifens.
Papierfaltung[Bearbeiten | Quelltext bearbeiten]
Bis zum fertigen Fünfeck sind nur drei Faltungen mit gleicher Faltrichtung und das Zusammenziehen des Überhandknotens erforderlich. Begonnen wird mit der Faltlinie , demzufolge das Trapez oberhalb des Streifenendes (Bild 4) zum liegen kommt. Der Punkt der Diagonale ist dabei direkt auf dem Punkt positioniert. Das regelmäßige Fünfeck kann man bereits jetzt erkennen.
Die zweite Faltung mit der Faltlinie (Bild 5) und dritte Faltung mit (Bild 6) werden analog zur ersten ausgeführt. Schließlich benötigt es nur noch das Durchziehen (Verknoten) des Streifenendes zwischen dem Streifenende und dem Trapez , um das gesuchte regelmäßige Fünfeck mit Goldenen Schnitt zu erhalten.[69]
-
Bild 4
Falten der ersten Faltlinie -
Bild 5
Falten der zweiten Faltlinie -
Bild 6
Falten der dritten und letzten Faltlinie , Streifenende zwischen dem Streifenende und dem Trapez durchgezogen
Weitere mathematische Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Algebraische Zahlentheorie[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt ist als Nullstelle des Polynoms eine algebraische Zahl. Weil das Polynom normiert ist und alle Koeffizienten ganzzahlig sind, ist der Goldene Schnitt sogar eine algebraisch ganze Zahl. Es sei , dann ist eine Körpererweiterung von Grad 2. Damit ist ein quadratischer Zahlkörper. Es ist der reell-quadratische Zahlkörper kleinster Diskriminante, nämlich 5 (der reell-quadratische Zahlkörper mit nächstgrößerer Diskriminante ist mit Diskriminante 8).[70] Es sei der zugehörige Ganzheitsring. Weil ganz ist, gilt , aber mehr als das: Wegen
ist der Goldene Schnitt sogar Einheit des Ganzheitsrings . Sein multiplikativ Inverses ist . Dies lässt sich algebraisch allein durch Kenntnis des Minimalpolynoms zeigen:
Jedoch ist der Goldene Schnitt nicht nur eine Einheit des Ganzheitsrings , sondern sogar Fundamentaleinheit des Ganzheitsrings. Das bedeutet, jedes Element aus ist von der Form mit . Darüber hinaus bilden eine -Basis von .[71] Das heißt, jedes Element aus lässt sich eindeutig als mit schreiben. Es bildet auch eine -Basis von . Dabei ist .
Kettenwurzel[Bearbeiten | Quelltext bearbeiten]
Aus lässt sich folgende unendliche Kettenwurzel herleiten:[72]
Setzt man also und mit , so gilt
- .
Hinsichtlich der Konvergenzgeschwindigkeit gilt
- , wobei . Es gilt die exakte Formel
- .
Sie kann auch implizit charakterisiert werden. Es bezeichne die für analytische Funktion, so dass die Differentialgleichung
sowie und erfüllt ist. Dann gilt .[73]
Trigonometrische und Hyperbolische Funktionen[Bearbeiten | Quelltext bearbeiten]
Aus der Trigonometrie folgt unter anderem[72]
und
- ,
sowie
- .
Es ist der volle Spitzwinkel und die Hälfte des stumpfen Außenwinkels des Pentagramms. Gelegentlich wird die Rolle des Goldenen Schnitts für das Fünfeck als vergleichbar bedeutend bezeichnet wie die der Kreiszahl für den Kreis. Ein weiterer Zusammenhang zur Kreiszahl ergibt sich über den Arkustangens, der Umkehrfunktion des Tangens aus der Trigonometrie. Es gilt[74]
- .
Der Goldene Schnitt lässt sich mit Hilfe der Eulerschen Zahl und der hyperbolischen Areasinus-Funktion ausdrücken:
Unendliche Reihen[Bearbeiten | Quelltext bearbeiten]
Einsetzen von in die für gültige geometrische Reihenformel ergibt:
- .
Es gilt zudem[72]
- .
Eine weitere Reihe, die den logarithmierten Goldenen Schnitt enthält, beinhaltet die mittleren Binomialkoeffizienten:
- .
Da gleichzeitig auch die Identität
für die nicht alternierende Variante gilt, wird hier eine „Verbindung“ zwischen der Kreiszahl und dem Goldenen Schnitt gesehen.[75]
Eine schnell konvergente Reihe beinhaltet die Fibonacci-Folge:
- .
Rogers-Ramanujan Kettenbrüche[Bearbeiten | Quelltext bearbeiten]
Es gilt[76]
- ,
- .
Dabei bezeichnet die Eulersche Zahl und die Kreiszahl. Setzt man für
so hat man allgemeiner für mit
- ,
sowie
- .
Diese Entdeckungen gehen auf Srinivasa Ramanujan zurück. Die Funktion wird auch als Rogers-Ramanujan-Kettenbruch bezeichnet und hat Verbindungen zur Theorie der Modulformen.[77]
Zusammenhang zur Chintschin-Levy-Konstante[Bearbeiten | Quelltext bearbeiten]
Definiert man den nächstgelegenen ganzzahligen Kettenbruch (englisch: nearest integer continued fraction) für reelle Zahlen via
über die Rekursion
so können die eventuell negative Zahlen sein. Für die Chintschin-Levy-Konstante gilt in diesem Falle
für alle betroffenen reellen Zahlen bis auf eine Lebesgue-Nullmenge.[78] Das bedeutet, dass alle Zahlen , „bis auf 0 %“ in einem asymptotischen Sinne, diese Gesetzmäßigkeit erfüllen. Ist zudem der (vollständig gekürzte) -te Näherungsbruch dieser Konstruktion, so gilt wieder bis auf Nullmenge[79]
- .
Alternierende Bit-Mengen[Bearbeiten | Quelltext bearbeiten]
Jede natürliche Zahl lässt sich eindeutig über das Binärsystem durch Nullen und Einsen ausdrücken. Innerhalb einer solchen Darstellung lassen sich nun sog. alternierende Bit-Mengen abzählen, die wie folgt erklärt sind:
- Von links nach rechts wechseln sich in den ausgewählten Positionen die Zahlen 1 und 0 ab.
- Die Zahl ganz zur Linken der ausgewählten Positionen ist 1.
- Die Zahl ganz zur Rechten der ausgewählten Positionen ist 0.
Man bezeichnet die Anzahl der alternierenden Bit-Mengen einer Zahl mit . Es ist zum Beispiel , denn im Binärsystem gilt , und daher sind die möglichen alternierenden Bit-Mengen (aus formalen Gründen inklusive der leeren Menge):
- .
Es bezieht sich z. B. auf . Es entspricht gleichzeitig der Anzahl der Möglichkeiten, als Summe von Zweierpotenzen zu schreiben, ohne dabei eine Potenz mehr als zweimal zu benutzen.[80] Diese zahlentheoretische Funktion hat eine Verbindung zum Goldenen Schnitt, denn es konnte
gezeigt werden. Dabei ist der Limes superior. Ob der innere Wert sogar 1 beträgt, konnte bisher nicht gezeigt werden.[81]
Verbindung zu speziellen Funktionen[Bearbeiten | Quelltext bearbeiten]
Über die Formel
wird eine direkte Verbindung zur Gammafunktion hergestellt.[82] Dabei ist wie üblich die Kreiszahl. Die Gammafunktion stellt eine Fortsetzung der Fakultätsfunktion auf komplexe Zahlen dar.
Für den Trilogarithmus gilt die Identität
- .
Dabei bezeichnet den Wert der Riemannschen Zeta-Funktion an der Stelle , der auch unter Apéry-Konstante bekannt ist.[83]
Varianten und Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Silberner Schnitt[Bearbeiten | Quelltext bearbeiten]

Der Silberne Schnitt beschreibt das definierte Größenverhältnis zweier Abschnitte mit unterschiedlicher Größe (oder Länge) einer Strecke (oder eines Bereichs).
Ist etwas „nach dem Silbernen Schnitt geteilt“, so versteht man darunter:
- Das Verhältnis der Summe des verdoppelten größeren und des kleineren Teils zum größeren Teil ist gleich dem Verhältnis des größeren zum kleineren Teil.
Es gilt also:
- .
Er hat den Wert[84]
Ebenso wie der Goldene Schnitt ist er also eine quadratisch-irrationale Zahl. Wegen gilt[85]
- .
Variante über Rechteckflächen[Bearbeiten | Quelltext bearbeiten]
Es soll eine gegebene Strecke mit der Länge um eine Länge verlängert werden, sodass ein Rechteck mit der Verlängerung als Breite und als Länge, gleich ist, einem vorab bestimmten Rechteck mit der Länge und der Breite . Es soll also[86]
gelten, was sich auf die quadratische Gleichung reduziert. Daraus ergibt sich über die Mitternachtsformel sogleich
da gelten soll. Ergeben Konstruktion oder Abmessungen des vorab bestimmten Rechtecks speziell
so ergibt sich zusätzlich
nach dem Umformen erhält man mit
das Teilungsverhältnis des Goldene Schnittes. Die Verlängerung ist in diesem Falle die mittlere Proportionale, sprich das geometrische Mittel, zwischen und .
Ephraim Salomon Unger zeigt seinen Weg, der zur Verlängerung führt:
„Man findet also die gesuchte Verlängerung, wenn man die mittlere Proportionale zwischen und als die eine Kathete und als die andere Kathete eines rechtwinkligen Dreiecks annimmt; und von der Hypotenuse desselben abschneidet.“

Konstruktion
(Die Konstruktion wurde, wegen nicht einsehbarer Skizze, der obigen Beschreibung von Unger nachempfunden.)
Es beginnt mit der Halbgeraden und dem Abtragen der gegebenen Strecke mit Länge auf . Der Punkt , für die Länge des (grünen) Rechtecks, wird rechts von beliebig auf gesetzt. Im allgemeinen Fall darf die Breite frei gewählt werden.
Soll hingegen zum Schluss der Punkt die gesuchte Strecke mit Länge im Goldenen Schnitt teilen, muss aus erst noch bestimmt werden. Hierfür wird die Breite des Rechtecks mittels des Quadrats mit Fläche durch die Verbindung der Punkte mit und deren Parallele festgelegt. Es folgt das Einzeichnen des Rechtecks , dessen Flächeninhalt mit gleich dem des Quadrates ist. Diese Vorgehensweise ist in der nebenstehenden Skizze dargestellt. Falls keine stetige Teilung erzielt werden soll, wird dieser erste Schritt weggelassen.
Es folgt der Kreisbogen mit Radius um bis er die Halbgerade in schneidet. Nach dem Bestimmen des Mittelpunktes der Strecke und dem Ziehen des Kreisbogens mit Radius um , wird die Senkrechte zu in errichtet, bis sie den Kreisbogen in schneidet. Die Strecke entspricht dem geometrischen Mittel der Längen und . Nach dem Halbieren der Strecke in wird mit Länge ab auf die Halbgerade übertragen und der so erzeugte Schnittpunkt mit verbunden. Daraus ergibt sich das rechtwinklige Dreieck . Der sich anschließende Kreisbogen mit Radius um liefert mit die gesuchte Länge . Die Übertragung der Länge auf ab erzeugt die Gesamtstrecke mit Länge .
Der Punkt teilt somit die Streckenlänge im Goldenen Schnitt, sofern gilt.
Das abschließend errichtete blaue Rechteck über mit der Breite hat ganz allgemein den gleichen Flächeninhalt wie das grüne Rechteck .
Kubische Varianten[Bearbeiten | Quelltext bearbeiten]
Man definiert die Perrin-Folge rekursiv durch , , , und für alle . Ähnlich wie sich die Quotienten nacheinander folgender Fibonacci-Zahlen dem Goldenen Schnitt nähern, folgt für die Perrin-Zahlen
wobei die charakteristische Gleichung erfüllt. Durch Radikale ausgedrückt ergibt sich
Ähnlich wie beim Goldenen Schnitt besitzt auch eine Entwicklung als Kettenwurzel, dieses Mal jedoch kubisch:
- .
In Anlehnung an Goldene Konstante wird gelegentlich auch als „Plastik-Konstante“ bezeichnet.[87]
Im Falle der „Tribonacci-Folge“ , und für gilt
- .
Es erfüllt die Gleichung .[88]
Verallgemeinerte Kettenbrüche[Bearbeiten | Quelltext bearbeiten]
Das Konzept der Kettenbruchentwicklung lässt sch für ganze positive Zahlen verallgemeinern durch
- .
Dies entspricht einer fraktalen Konstruktion durch die iterative Anwendung der Ersetzungsregeln
- .
Dieser verallgemeinerte Kettenbruch konvergiert stets gegen die positive Lösung der Gleichung[89]
- .
Setzt man in diesem Beispiel also insbesondere , so ergibt sich als Grenzwert die Zahl , die eine kubische Verallgemeinerung des Goldenen Schnittes darstellt.[90]
Asymptotik zufälliger Fibonacci-Folgen[Bearbeiten | Quelltext bearbeiten]
Setzt man , sowie
für , wobei die Vorzeichen durch unabhängige Zufallsvariablen mit gleichen Wahrscheinlichkeiten für gegeben sind, zeigte D. Viswanadt[91]
mit Wahrscheinlichkeit 1. Die gewöhnliche Fibonacci-Folge, die sich in dieser Art Limes dem Goldenen Schnitt annähert, entspricht dem Extremfall, dass die Zufallsgrößen stets den Wert annehmen, was aber mit einer (asymptotischen) Wahrscheinlichkeit von 0 Prozent eintritt.[92]
Vorkommen in der Natur[Bearbeiten | Quelltext bearbeiten]
Biologie[Bearbeiten | Quelltext bearbeiten]

Das spektakulärste Beispiel für Verhältnisse des Goldenen Schnittes in der Natur findet sich bei der Anordnung von Blättern (Phyllotaxis) und in Blütenständen mancher Pflanzen.[93] Bei diesen Pflanzen teilt der Winkel – wie im Bild vereinfacht dargestellt – zwischen zwei aufeinanderfolgenden Blättern den Vollkreis von 360° im Verhältnis des Goldenen Schnittes, wenn die beiden Blattansätze durch eine Parallelverschiebung eines der Blätter entlang der Pflanzenachse zur Deckung gebracht werden. Es handelt sich um den Goldenen Winkel von etwa 137,5°.
Die daraus entstehenden Strukturen werden auch als selbstähnlich bezeichnet: Auf diese Weise findet sich ein Muster einer tieferen Strukturebene in höheren Ebenen wieder. Beispiele sind die Sonnenblume,[94] Kohlarten, Kiefernnadeln an jungen Ästen, Zapfen,[95] Agaven, viele Palmen- und Yuccaarten sowie die Blütenblätter der Rose, um nur einige zu nennen.
Ursache ist das Bestreben dieser Pflanzen, ihre Blätter auf Abstand zu halten. Es wird vermutet, dass sie dazu an jedem Blattansatz einen besonderen Wachstumshemmer (Inhibitor) erzeugen, der im Pflanzenstamm – vor allem nach oben, in geringerem Umfang in seitlicher Richtung – diffundiert. Dabei bilden sich in verschiedene Richtungen bestimmte Konzentrationsgefälle aus. Das nächste Blatt entwickelt sich an einer Stelle des Umfangs, wo die Konzentration minimal ist. Dabei stellt sich ein bestimmter Winkel zum Vorgänger ein. Würde dieser Winkel den Vollkreis im Verhältnis einer rationalen Zahl teilen, dann würde dieses Blatt genau in die gleiche Richtung wachsen wie dasjenige Blätter zuvor. Der Beitrag dieses Blattes zur Konzentration des Inhibitors ist aber an dieser Stelle gerade maximal. Daher stellt sich ein Winkel mit einem Verhältnis ein, das alle rationalen Zahlen meidet. Die Zahl ist nun aber gerade die Goldene Zahl (siehe oben). Da bisher kein solcher Inhibitor isoliert werden konnte, werden auch andere Hypothesen diskutiert, wie die Steuerung dieser Vorgänge in analoger Weise durch Konzentrationsverteilungen von Nährstoffen.
Der Nutzen für die Pflanze könnte darin bestehen, dass auf diese Weise von oben einfallendes Sonnenlicht (bzw. Wasser und Luft) optimal genutzt wird,[96] eine Vermutung, die bereits Leonardo da Vinci äußerte, oder im effizienteren Transport der durch Photosynthese entstandenen Kohlenhydrate im Phloemteil der Leitbündel nach unten. Die Wurzeln von Pflanzen weisen den Goldenen Winkel weniger deutlich auf. Bei anderen Pflanzen wiederum treten Blattspiralen mit anderen Stellungswinkeln zutage. So wird bei manchen Kakteenarten ein Winkel von 99,5° beobachtet, der mit der Variante der Fibonacci-Folge 1, 3, 4, 7, 11, … korrespondiert. In Computersimulationen des Pflanzenwachstums lassen sich diese verschiedenen Verhaltensweisen durch geeignete Wahl der Diffusionskoeffizienten des Inhibitors provozieren.

Bei vielen nach dem Goldenen Schnitt organisierten Pflanzen bilden sich in diesem Zusammenhang so genannte Fibonacci-Spiralen aus. Spiralen dieser Art sind besonders gut zu erkennen, wenn der Blattabstand im Vergleich zum Umfang der Pflanzenachse besonders klein ist. Sie werden nicht von aufeinanderfolgenden Blättern gebildet, sondern von solchen im Abstand , wobei eine Fibonacci-Zahl ist. Solche Blätter befinden sich in enger Nachbarschaft, denn das -Fache des Goldenen Winkels ist ungefähr ein Vielfaches von 360° wegen
- ,
wobei die nächstkleinere Fibonacci-Zahl zu und die nächstkleinere Fibonacci-Zahl zu ist. Da jedes der Blätter zwischen diesen beiden zu einer anderen Spirale gehört, sind Spiralen zu sehen. Ist größer als , so ist das Verhältnis der beiden nächsten Fibonacci-Zahlen kleiner und umgekehrt. Daher sind in beide Richtungen Spiralen zu aufeinander folgenden Fibonaccizahlen zu sehen. Der Drehsinn der beiden Spiralentypen ist dem Zufall überlassen, sodass beide Möglichkeiten gleich häufig auftreten.

Besonders beeindruckend sind Fibonacci-Spiralen (die damit wiederum dem Goldenen Schnitt zugeordnet sind) in Blütenständen, wie bei Sonnenblumen.[94] Dort sitzen Blüten, aus denen später Früchte entstehen, auf der stark gestauchten, scheibenförmigen Blütenstandsachse dicht nebeneinander, wobei jede einzelne Blüte einem eigenen Kreis um den Mittelpunkt des Blütenstandes zugeordnet werden kann. Wachstumstechnisch aufeinander folgende Früchte liegen daher räumlich weit auseinander, während direkte Nachbarn wieder einen Abstand entsprechend einer Fibonacci-Zahl haben. Im äußeren Bereich von Sonnenblumen werden 34 und 55 Spiralen gezählt, bei größeren Exemplaren 55 und 89 oder sogar 89 und 144. Die Abweichung vom mathematischen Goldenen Winkel, die in diesem Fall nicht überschritten wird, beträgt weniger als 0,01 %.
Der Goldene Schnitt ist außerdem in radiärsymmetrischen fünfzähligen Blüten erkennbar wie bei der Glockenblume, der Akelei und der (wilden) Hecken-Rose. Der Abstand der Spitzen von Blütenblättern nächster Nachbarn zu dem der übernächsten steht wie beim regelmäßigen Fünfeck üblich in seinem Verhältnis. Das betrifft ebenso Seesterne und andere Tiere mit fünfzähliger Symmetrie.[95]

Darüber hinaus wird der Goldene Schnitt im Verhältnis der Längen aufeinander folgender Stängelabschnitte mancher Pflanzen vermutet wie bei der Pappel. Im Efeublatt stehen die Blattachsen a und b (siehe Abbildung) ungefähr im Verhältnis des Goldenen Schnittes. Diese Beispiele sind jedoch umstritten.
Noch im 19. Jahrhundert war die Ansicht weit verbreitet, dass der Goldene Schnitt ein göttliches Naturgesetz sei und in vielfacher Weise in den Proportionen des menschlichen Körpers realisiert wäre. So nahm Adolf Zeising in seinem Buch über die Proportionen des menschlichen Körpers[20] an, dass der Nabel die Körpergröße im Verhältnis des Goldenen Schnittes teile, und der untere Abschnitt werde durch das Knie wiederum so geteilt. Ferner scheinen die Verhältnisse benachbarter Teile der Gliedmaßen wie bei Ober- und Unterarm sowie bei den Fingerknochen ungefähr in diesem Verhältnis zu stehen. Eine genaue Überprüfung ergibt jedoch Streuungen der Verhältnisse im 20-%-Bereich. Oft enthält auch die Definition, wie die Länge eines Körperteils exakt zu bestimmen sei, eine gewisse Portion Willkür. Ferner fehlt dieser These eine wissenschaftliche Grundlage. Es dominiert daher weitgehend die Ansicht, dass diese Beobachtungen lediglich die Folge gezielter Selektion von benachbarten Paaren aus einer Menge von beliebigen Größen sind.[97]
Bahnresonanzen[Bearbeiten | Quelltext bearbeiten]
Seit langem ist bekannt, dass die Umlaufzeiten mancher Planeten und Monde in Verhältnis kleiner ganzer Zahlen stehen wie Jupiter und Saturn mit oder die Jupitermonde Io, Ganymed und Europa mit . Derartige Bahnresonanzen stabilisieren die Bahnen der Himmelskörper langfristig gegen kleinere Störungen. Erst 1964 wurde entdeckt, dass noble Verhältnisse, wie sie im Fall vorliegen würden, stabilisierend wirken können. Derartige Bahnen werden KAM-Bahnen genannt, wobei die drei Buchstaben für die Namen der Entdecker Andrei Kolmogorow, V. I. Arnold und Jürgen Moser stehen.[98][99]
Die Cassini-Teilungen in den Saturnringen zeigen, was passiert, wenn statt nobler Zahlen einfache rationale Zahlen vorherrschen: Die Gesteins- und Eisteilchen, aus denen die Ringe bestehen und deren Umlaufperioden in einem einfachen rationalen Verhältnis zu den Perioden der Saturnmonde stehen, werden durch die Resonanzeffekte zwischen den entsprechenden Umlaufperioden einfach aus ihrer Bahn geworfen. In der Tat hängt die Stabilität des Sonnensystems davon ab, dass zumindest einige der Bahnperiodenverhältnisse nobel sind.[100]
Schwarze Löcher[Bearbeiten | Quelltext bearbeiten]
Kontrahierbare kosmische Objekte ohne feste Oberfläche, wie Schwarze Löcher oder die Sonne, haben aufgrund ihrer Eigengravitation die paradoxe Eigenschaft, heißer zu werden, wenn sie Wärme abstrahlen (negative Wärmekapazität). Bei rotierenden Schwarzen Löchern findet ab einem kritischen Drehimpuls ein Umschlag von negativer zu positiver Wärmekapazität statt, wobei dieser Tipping-Point von der Masse des Schwarzen Loches abhängt. In einer -dimensionalen Raumzeit kommt dabei eine Metrik ins Spiel, deren Eigenwerte für sich als Nullstellen des charakteristischen Polynoms
Kristallstrukturen[Bearbeiten | Quelltext bearbeiten]
Quasikristalle[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt tritt bei den Quasikristallen der Festkörperphysik in Erscheinung, die 1984 von Dan Shechtman und seinen Kollegen entdeckt wurden.[103] Dabei handelt es sich um Strukturen mit fünfzähliger Symmetrie, aus denen sich aber, wie bereits Kepler erkannte, keine streng periodischen Kristallgitter aufbauen lassen, wie dies bei Kristallen üblich ist. Entsprechend groß war die Überraschung, als bei Röntgenstrukturanalysen Beugungsbilder mit fünfzähliger Symmetrie gefunden wurden. Diese Quasikristalle bestehen strukturell aus zwei verschiedenen rhomboedrischen Grundbausteinen, mit denen der Raum zwar lückenlos, jedoch ohne globale Periodizität gefüllt werden kann (Penrose-Parkettierung). Beide Rhomboeder setzten sich aus den gleichen rautenförmigen Seitenflächen zusammen, die jedoch unterschiedlich orientiert sind. Die Form dieser Rauten lässt sich nun dadurch definieren, dass ihre Diagonalen im Verhältnis des Goldenen Schnittes stehen. Für die Entdeckung von Quasikristallen wurde Shechtman 2011 der Nobelpreis für Chemie verliehen.[24]
Kobalt-Niobat[Bearbeiten | Quelltext bearbeiten]
Im atomaren Aufbau des Kristalls aus Kobalt-Niobat entdeckten Forscher des Helmholtz-Zentrums Berlin für Materialien und Energie (HZB) Symmetrieeigenschaften erstmal in fester Materie, die auch den Goldenen Schnitt kennzeichnen (veröffentlicht in der Zeitschrift Science, Januar 2010). Für Untersuchungen der Quanteneigenschaften, sprich Verhalten atomarer Teilchen in der Quantenwelt nach Heisenbergs Unschärferelation, findet Kobalt-Niobat Verwendung. Ausschlaggebend dafür sind insbesondere, die auf besondere Weise angeordneten atomaren Bestandteile sowie die magnetischen Eigenschaften des Kristalls. Dies bedeutet, hervorgerufen durch den im Elektron vorhandenen Eigenimpuls (Spin), bilden in diesem Kristall die aneinandergereihten Atome eine sogenannte Spinkette mit der Wirkung eines dünnen Stabmagnets. Wirkt nun ein Magnetfeld rechtwinklig auf die Spinkette, geht sie in einen neuen Zustand über. Physiker stellen sich diesen Zustand als fraktales Muster vor.
Als die Forscher dies als Modell für die Untersuchung des Festkörpermagnetismus nutzten, machten sie eine überraschende Entdeckung: Die Wechselwirkung, die benachbarte Spinketten miteinander eingehen, entspricht der Schwingung einer Gitarrensaite, deren ersten beiden Resonanzfrequenzen im Verhältnis , zueinander stehen. „Was genau dem Goldenen Schnitt entspricht“, so Radu Coldea, Leiter des über zehn Jahre laufenden internationalen Projektes.[25]
Vergleich mit anderen prominenten Seitenverhältnissen[Bearbeiten | Quelltext bearbeiten]
Die folgende Abbildung zeigt im Vergleich verschiedene Rechtecke mit prominenten Seitenverhältnissen in der Umgebung von Angegeben ist jeweils das Verhältnis von Höhe zu Breite und der entsprechende Zahlenfaktor:
- – Traditionelles Fernsehformat und Ballenformat für Packpapier. Auch bei älteren Computermonitoren verwendet (z. B.: 1024 × 768 Pixel). Dieses Format geht zurück auf Thomas Alva Edison, der 1889 das Format des klassischen Filmbildes (35-mm-Film) auf 24 mm × 18 mm festlegte.[104]
- – Das Seitenverhältnis beim DIN-A4-Blatt und verwandten DIN-/EN-/
ISO-Maßen. Bei einer Halbierung durch einen Schnitt, der die längeren Seiten des Rechtecks halbiert, entstehen wiederum Rechtecke mit demselben Seitenverhältnis. - – Seitenverhältnis beim Kleinbildfilm (36 mm × 24 mm).
- – Manche Computerbildschirme (1920 × 1200 Pixel). Diese passen mit 1,6 : 1 fast zum Goldenen Schnitt.
- – Seitenverhältnis im Goldenen Schnitt. Im Bild approximiert mit 144 × 89 Pixel (theoretischer Fehler nur 5 · 10−5). Die beiden benachbarten Rechtecke 3:2 und 5:3 haben – wie auch das dargestellte Rechteck mit 144:89 – Seitenverhältnisse von aufeinanderfolgenden Fibonacci-Zahlen und approximieren daher ebenfalls den Goldenen Schnitt vergleichsweise gut.
- – Findet neben vielen anderen als Kinofilmformat Verwendung.
- – Breitbildfernsehen.
Anwendung in Technik und Mathematik[Bearbeiten | Quelltext bearbeiten]
Der Goldene Zirkel (Reduktionszirkel)[Bearbeiten | Quelltext bearbeiten]
Anstatt stets neu konstruieren zu müssen, wurde im 19. Jahrhundert von Künstlern und Handwerkern ein Goldener Zirkel – ein auf das Goldene Verhältnis eingestellter Reduktionszirkel – benutzt. Insbesondere im Schreinerhandwerk kam ein ähnliches Instrument in Form eines Storchschnabels zur Anwendung.[105] Bereits in der Antike fand der Reduktionszirkel Verwendung, dies zeigt z. B. der Fund eines Vorläufers bei den Ausgrabungen in Pompeji.[106] Solche Zirkel, wie die im Folgenden näher beschriebenen Beispiele, werden auch heute noch hergestellt. Die einfachste Ausführung besteht nur aus zwei Stäben – in moderner Bauweise zusätzlich mit vier Nadeln – deren Drehpunkt sie im Goldenen Schnitt teilt.[107]
Für die Lage des Drehpunktes gilt:
- .
-
Lage des Drehpunktes
Mithilfe eines solchen Reduktionszirkels gelingt die Teilung einer gegebenen Streckenlänge in (innere Teilung) sowie die Verlängerung einer Strecke um die Länge (äußere Teilung). Punkt teilt die Streckenlänge im Goldenen Schnitt.
Der von Adalbert Göringer im Jahre 1893 erfundene Reduktions- bzw. Proportionalzirkel – dargestellt in den nebenstehenden Bildern – ist eine Weiterentwicklung.[108] Um als Werkzeug für die innere und äußere Teilung dienen zu können, müssen die Bauteile des Reduktionszirkels ebenfalls die Teilung nach dem Goldenen Schnitt beinhalten.
Wenn
- ,
dann gilt:
- .
Rechteck mit einbeschriebenem Dreieck[Bearbeiten | Quelltext bearbeiten]

„Man beschreibe in ein gegebenes Rechteck ein Dreieck (das mit dem Rechteck eine Ecke gemeinsam hat) so ein, daß die drei dabei entstehenden Dreiecke die gleiche Fläche haben.“
Die Flächengleichheit bedeutet, dass gilt.
Aus der Gleichheit des ersten und zweiten Terms folgt (1) und aus der Gleichheit des ersten und dritten Terms (2).
Aus (1) und (2) ergibt sich:
- .
Wegen
gilt dann auch:[109]
Gleichschenkliges Dreieck, gegebene Strecke teilt gesuchten Schenkel im Goldenen Schnitt[Bearbeiten | Quelltext bearbeiten]

( von und ) sowie „diesen Schnitt den goldenen“[16] als Konstruktionselement.
Von M. Johann Wentzel Kaschube stammt die im Folgenden beschriebene und im Anschluss konstruktiv dargestellte geometrische Aufgabe aus dem Jahr 1717.
„§.34. Einen gleichschencklichten , in welchem der auf einem Schenckel stehende perpendicul gegeben, so den Schenckel selbst in auf solche Arth schneidet, wie er von den übrigen perpend. Linien in geschnitten wird, kan auf folgende Weise gefunden werden. […]“
Gesucht ist also ein gleichschenkliges Dreieck, in dem eine gegebene Strecke sowie ein Schenkel des Dreiecks zueinander orthogonal sind und der Punkt diesen Schenkel im Verhältnis des Goldenen Schnitts teilt.
Konstruktionsbeschreibung
(Angelehnt an die Beschreibung des Originals, die darin erwähnte Fig. 7 ist auf Tab. I Alg. Fig. 8)[111]
Zuerst wird die Strecke mit der frei wählbaren Länge senkrecht auf die Gerade errichtet. Es folgt das rechtwinklige Dreieck , in dem die Seite mit Länge auf der Geraden liegt. Der Kreisbogen um mit Radius ergibt Schnittpunkt , der Kreisbogen um mit Radius teilt in die Seite im Goldenen Schnitt. Ziehe einen Kreis um mit Radius , ergibt Schnittpunkt und einen Kreisbogen um mit Radius . Nun errichte eine Senkrechte auf ab bis sie den Kreisbogen in schneidet. Mit ist das geometrische Mittel der beiden Streckenlängen und bestimmt. Ein Kreisbogen um mit Radius schneidet den Kreis um in , und dabei ergibt sich das rechtwinklige Dreieck . Abschließend wird die Strecke bis auf die Gerade verlängert und um den soeben entstandenen Schnittpunkt ein Kreisbogen mit Radius gezogen, bis er die Gerade in schneidet.
Im somit gefundenen gleichschenkligen Dreieck teilt der Punkt der Senkrechten den Schenkel im Goldenen Schnitt.
Dreiecksfraktal[Bearbeiten | Quelltext bearbeiten]

Ab 1975 sind in der Mathematik die unterschiedlichsten Fraktale entwickelt worden.
Das folgende Fraktal – mit sieben Iterationsschritten – verwendet ein gleichseitiges Dreieck als Ausgangsform. An seinen Ecken wird ein Dreieck mit einem bestimmten Verkleinerungsfaktor [112] Spitze an Spitze angehängt. Der Verkleinerungsfaktor wird so gewählt, dass das Verhältnis der Seitenlängen zueinander dem Teilungsverhältnis des Goldenen Schnittes entspricht.
Fraktale werden meist mithilfe eines Computers erstellt. Dieses zweidimensionale Dreiecksfraktal ist – mit entsprechendem Aufwand – auch als Konstruktion mit Zirkel und Lineal darstellbar.
Skizze[Bearbeiten | Quelltext bearbeiten]

Anhand der nebenstehenden Skizze wird der Verkleinerungsfaktor , die gewünschte Anzahl der Äste (Dreiecke) und somit auch der Abstand der letzten Äste zueinander grafisch bestimmt.[112]
Es beginnt mit der Konstruktion eines gleichseitigen Dreiecks mit der Seitenlänge gleich . Halbiert man nun dessen beide Schenkel und zieht die Gerade durch die soeben erhaltenen Mittelpunkte, ergibt sich das gleichseitige (grüne) Ausgangsdreieck des Fraktals mit Seitenlänge gleich . Es folgen zwei Verbindungslinien, jeweils ab dem Mittelpunkt der Schenkel bis zur gegenüberliegenden Ecke des Dreiecks. Sie schneiden sich im Mittelpunkt des Umkreises des großen Dreiecks. Beim Ziehen des Umkreises ergibt sich, mittels der Schnittpunkte auf der Geraden , der gesuchte Verkleinerungsfaktor links und rechts vom Ausgangsdreieck.
Nachweis des Verkleinerungsfaktors f[Bearbeiten | Quelltext bearbeiten]

Die oben beschriebenen Konstruktionsschritte gleichen denen der Konstruktion nach Odom.
Somit gilt in diesem Fall:
daraus folgt
Die in der Skizze mit gepunkteten Linien angedeutete Konstruktion zeigt: Die Seitenlängen (Kreisradien) für die nachfolgenden, noch gut im Fraktal erkennbaren Dreiecke, ergeben sich, indem man für das nächste Dreieck den Exponent des Verkleinerungsfaktors um erhöht:
Beutelspacher ermittelte in Der Goldene Schnitt den Wert des Abstandes, bei dem sich die entgegenkommenden Äste im Grenzfall berühren, letztendlich aus der kubischen Gleichung (siehe nebenstehendes Bild)
- ;
deren einzige positiven Lösung ist
- .
Somit ist aufgezeigt: ist nicht nur der Wert des Verkleinerungsfaktors, sondern auch der Wert des Abstandes, bei dem sich im Grenzfall die einzelnen Äste berühren, sprich gerade noch nicht überlappen.[112]
Papier- und Bildformate[Bearbeiten | Quelltext bearbeiten]
Im Buchdruck wurde gelegentlich die Nutzfläche einer Seite, der sogenannte Satzspiegel, so positioniert, dass das Verhältnis von Bundsteg zu Kopfsteg zu Außensteg zu Fußsteg sich wie verhielt. Diese Wahl von Fibonacci-Zahlen approximiert den Goldenen Schnitt. Eine solche Gestaltung wird auch weiterhin in Teilen der Fachliteratur zum Buchdruck empfohlen.[113]
Anwendung in der bildenden Kunst[Bearbeiten | Quelltext bearbeiten]
Seit dem 19. Jahrhundert wurde der Goldene Schnitt zunächst in der ästhetischen Theorie (Adolf Zeising) und dann auch in künstlerischer, architektonischer und kunsthandwerklicher Praxis als ein ideales Prinzip ästhetischer Proportionierung bewertet. Er soll besonders angenehm, ansprechend, ausgewogen, harmonisch und schön wirken. Es gibt allerdings keinen empirischen Beleg für eine besondere ästhetische Wirkung, die von Proportionen des Goldenen Schnittes ausgeht.[114] Schon der Begründer der empirischen Ästhetik, Gustav Theodor Fechner, stellte aufgrund eigener Experimente fest: „Hiernach kann ich nicht umhin, den ästhetischen Wert des Goldenen Schnittes … überschätzt zu finden.“[115]
Architektur[Bearbeiten | Quelltext bearbeiten]


Frühe Hinweise auf eine Verwendung des Goldenen Schnittes stammen aus der Architektur. Die Schriften des griechischen Geschichtsschreibers Herodot zur Cheops-Pyramide werden gelegentlich dahingehend ausgelegt, dass die Höhe der Seitenfläche zur Hälfte der Basiskante im Verhältnis des Goldenen Schnittes stünde.[116] Die entsprechende Textstelle ist allerdings interpretierbar. Andererseits wird die These vertreten, dass das Verhältnis für Pyramidenhöhe zu Basiskante die tatsächlichen Maße noch besser widerspiegele. Der Unterschied zwischen beiden vertretenen Thesen beträgt zwar lediglich 3,0 %, ein absoluter Beweis zugunsten der einen oder anderen These ist demzufolge damit aber nicht verbunden.
Viele Werke der griechischen Antike werden als Beispiele für die Verwendung des Goldenen Schnittes angesehen wie die Vorderfront des 447–432 v. Chr. unter Perikles erbauten Parthenon-Tempels auf der Athener Akropolis.[117] Da zu diesen Werken keine Pläne überliefert sind, ist nicht bekannt, ob diese Proportionen bewusst oder intuitiv gewählt wurden. In späteren Epochen sind mögliche Beispiele für den Goldenen Schnitt, wie der Dom von Florenz,[118] Notre Dame in Paris[119][120] oder die Torhalle in Lorsch (770 n. Chr.)[117] zu finden. Auch in diesen Fällen ist die bewusste Anwendung des Goldenen Schnittes anhand der historischen Quellen nicht nachweisbar.
Es gibt demzufolge keinen empirisch gesicherten Nachweis für eine signifikant größere Häufigkeit des Goldenen Schnittes in diesen Epochen im Vergleich zu anderen Teilungsverhältnissen. Ebenso fehlen historische Belege für eine absichtliche Verwendung des Goldenen Schnittes.
Als ein Beispiel für eine Umsetzung des Goldenen Schnittes wird immer wieder das Alte Rathaus in Leipzig, ein Renaissancebau aus den Jahren 1556/57, genannt.[121] Wobei nicht die Mitte des Rathausturmes die Gehäusefront im Goldenen Schnitt teilt, sondern die dazu etwas versetzte Mitte des Haupttores. Gleichwohl gibt es bei genauer historischer Quellenforschung keinen Beleg dafür. Insbesondere gibt es keinen Beleg dafür, dass Hieronymus Lotter als der damalige Baumeister den Goldenen Schnitt bewusst als Konstruktionsprinzip verwendet hat: Alle originären Quellen verweisen lediglich auf einen gotischen Vorgängerbau, auf dessen Grundmauern Lotter das Rathaus errichtet hat. Dass der Goldene Schnitt hier eine Rolle gespielt habe, ist quellenhistorisch nicht belegbar.
Die erste quellenhistorisch gesicherte Verwendung des Goldenen Schnittes in der Architektur stammt aus dem 20. Jahrhundert: Der Architekt und Maler Le Corbusier (1887–1965) entwickelte ab 1940 ein Längen-Maßsystem, dessen Maßeinheiten zueinander im Verhältnis des Goldenen Schnitts stehen. Die Werte der darin enthaltenen kleineren Maßeinheiten sind Durchschnitts-Maße am menschlichen Körper. Er veröffentlichte dieses 1949 in seiner Schrift Der Modulor, die zu den bedeutendsten Schriften der Architekturgeschichte und -theorie gezählt wird. Bereits 1934 wurde ihm für die Anwendung mathematischer Ordnungsprinzipien von der Universität Zürich der Titel doctor honoris causa der mathematischen Wissenschaften verliehen.[122] Für eine frühere Verwendung des Modulors ist dies jedoch aus den aufgezeigten Gründen kein Beleg.
Plastik und Malerei[Bearbeiten | Quelltext bearbeiten]
Für die generelle These, dass der Goldene Schnitt als besonders ansprechend und harmonisch empfunden wird, gibt es keine gesicherten Belege und ist letztlich eine Frage der jeweils herrschenden Kunstauffassung. Viele Künstler setzten den Goldenen Schnitt bewusst ein, bei vielen Werken wurden Kunsthistoriker erst im Nachhinein fündig. Diese Befunde sind jedoch angesichts der Fülle von möglichen Strukturen, wie sie in einem reich strukturierten Gemälde zu finden sind, oft umstritten.[123]
So werden zahlreichen Skulpturen griechischer Bildhauer, wie der Apollo von Belvedere, der Leochares (um 325 v. Chr.) zugeschrieben wird, oder Werke von Phidias (5. Jahrhundert v. Chr.) als Beispiele für die Verwendung des Goldenen Schnittes angesehen. Auf letzteren bezieht sich die oft übliche Bezeichnung für den Goldenen Schnitt, die ungefähr 1909 von dem amerikanischen Mathematiker Mark Barr eingeführt wurde.[124] Die ebenfalls gelegentlich verwendete Bezeichnung bezieht sich dagegen auf das griechische Wort τομή tomé für „Schnitt“.[125]

Der Goldene Schnitt wird in vielen Werken der Renaissance-Künstler vermutet, unter anderem bei Raffael, Leonardo da Vinci und Albrecht Dürer, bei Dürers Werken insbesondere in seinem Selbstbildnis von 1500 und seinem Kupferstich Melencolia I von 1514.[127]
Ein berühmtes Beispiel ist das Gemälde Mona Lisa von Leonardo da Vinci. Es weist Merkmale des Goldenen Schnitts auf und lässt mehrere Goldene Dreiecke sowie die Goldene Spirale erkennen. In Abbildung 1 teilt der Punkt (Mona Lisas linkes Auge) die Strecken und im Goldenen Schnitt. Die Dreiecke und sind Goldene Dreiecke, da bei jedem dieser sechs Dreiecke Grundseite und Schenkel im Verhältnis des Goldenen Schnitts zueinander stehen.[128][129] In Abbildung 2 ist die Goldene Spirale eingezeichnet. Sie ist so positioniert, dass sie am linken Handgelenk beginnt und den oberen Rand des Kopfes berührt. Die Nasenspitze bildet dann den Punkt, auf den die Spirale zuläuft.[130][131]
Bekanntlich stellte auch Albrecht Dürer zahlreiche theoretische Untersuchungen an und beschäftigte sich mit mathematischen Fragestellungen. Im Zusammenhang mit dem Goldenen Schnitt ist besonders interessant, dass er in seiner Underweysung der messung 1525 ein in einen Kreis einbeschriebenes Fünfeck konstruiert. Daher gilt es nicht als ausgeschlossen, dass Dürer in seinen Bildern den Goldenen Schnitt verwendet hat. Allerdings hat Dürer in seinen theoretischen Arbeiten den Goldenen Schnitt an keiner Stelle erwähnt.[132]
Auch im 19. und 20. Jahrhundert spielte der Goldene Schnitt bei manchen Vertretern der bildenden Kunst eine Rolle. Georges Seurat (1859–1891), der Begründer des Neoimpressionismus, strebte einen streng geometrischen Bildaufbau an[133] und verwendet in allen seinen großformatigen Bildern den Goldenen Schnitt. Besonders deutlich ist dies in seinem Gemälde Die Zirkusparade. Neben einem goldenen Rechteck lassen sich etliche Einteilungslinien nach dem Goldenen Schnitt erkennen.[134] Allerdings existieren In einer vorbereitenden Zeichnung lediglich Linien, die nicht mit dem Goldenen Schnitt korrespondieren.[126] Damit bleibt offen, ob Seurat den Goldenen Schnitt bewusst oder intuitiv angewandt hat.
In der Fotografie wird der Goldene Schnitt zur Bildgestaltung eingesetzt. Als Faustformel wird die Drittel-Regel verwendet.[135][136]
Zeitgenössische bildende Kunst[Bearbeiten | Quelltext bearbeiten]

Irene Schramm-Biermann
In der zeitgenössischen bildenden Kunst wird der Goldene Schnitt nicht nur als Gestaltungsmerkmal verwendet, sondern ist in manchen Arbeiten selbst Thema oder zentraler Bildinhalt.
Bei Joseph Beuys kommt der Goldene Schnitt bei den Besprechungen der Arbeiten seiner Schülerinnen und Schüler oft als positiver Orientierungspunkt zur Sprache.[137] Der Künstler Jo Niemeyer verwendet den Goldenen Schnitt als grundlegendes Gestaltungsprinzip in seinen Werken, die der konkreten Kunst zugeordnet werden. Der Künstler Ivo Ringe, der ebenso ein Vertreter der konkreten Kunst ist, nutzt den Goldenen Schnitt in vielen seiner Werke.[138] Die Künstlerin Martina Schettina thematisiert den Goldenen Schnitt in ihren Arbeiten zum Fünfeck, bei dem die Diagonalen einander im Goldenen Schnitt teilen.[139] Sie visualisiert auch die Konstruktionsmethode und Formeln zum Goldenen Schnitt.[140] Irene Schramm-Biermann legt ihre künstlerischen Schwerpunkte auf Konkrete Kunst mit Bezug zur Mathematik und Landschaften. Die Darstellung im nebenstehende Bild lässt für den Betrachter offen: Resultiert die Goldene Spirale aus dem Goldenen Dreieck, oder war die Spirale der Ursprung?
Verwendung in Literatur und Musik[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt wurde auch zur Gestaltung literarischer Werke herangezogen.
Das vom römischen Dichter Vergil (70–19 v. Chr.) geschaffene Werk Äneis gilt als älteste bekannte Literatur, die auf dem Goldenen Schnitt aufbaut. Bei Untersuchungen wurden Zeilen in verschiedenen Abschnitten gezählt, wobei festgestellt wurde, dass deren Verhältnisse dem Goldenen Schnitt meist recht nahe kommen. Allerdings wurde genau dieser „Abstandsbegriff“ weit ausgelegt, wobei etwa Werte wie 0,6 und 0,636 als Annäherung von 0,618… akzeptiert wurden. Zudem finden sich im Text zahlreiche Halbverse (unvollständige Zeilen), die auf mangelnde redaktionelle Überarbeitung seitens Vergils zurückgeführt werden. Nach Bereinigung ergab sich in ca. 75 % aller Fälle eine bessere Annäherung an den Goldenen Schnitt. Die Studie wurde jedoch auch kritisch rezipiert.[141]
Vor dem Hintergrund der verbreiteten Zahlensymbolik im Mittelalter wurde das Liber ymnorum des Notker Balbulus (um 885) genauer untersucht. Dabei kam heraus, dass einige Segmente dieses Hymnus gemäß dem Goldenen Schnitt aufgebaut sind. Genauer gilt, dass die Anzahl der Silben im ersten Teil und der im zweiten Teil annähernd im Verhältnis des Goldenen Schnittes liegen. Als ein Beispiel wird auf den Laurentiushymnus verwiesen: In den ersten 144 Silben wird Laurentius angerufen und sein Martyrium gerühmt. Im Anschluss wird er 89 Silben lang um Fürbitte gebeten. Es bleibt jedoch unklar, ob das Auftreten dieser (großen) Fibonacci-Zahlen 89 und 144, ca. 300 Jahre vor Fibonacci, ein Zufall ist.[142]
Nach Meinung von J. Benjafield und C. Davis enthalten Grimms Märchen den Goldenen Schnitt in einer „besonders unerwarteten Form“. Sie teilten sämtliche „585 Charakteren (Personen, sprechende Tiere, …) aus den 125 Märchen“[143] über die Eigenschaften gut – böse, stark – schwach und aktiv – passiv in 8 mögliche Gruppen ein. Die Gruppen 1–4 haben sie mit „gut, stark, aktiv“, „gut, stark, passiv“, „gut, schwach, aktiv“ und „böse, stark, aktiv“ als positiv bezeichnet, die Gruppen 5–8 als negativ. Es stellt sich nach dieser Gruppierung heraus, dass zwischen 60 % und 62 % (z. B. 100 : 62 = 1,6129 ...) der Märchencharaktere positiv sind. Als Erklärung dieses „Zusammenhangs“ wird darauf verwiesen, dass der Goldene Schnitt in der Natur sehr häufig auftrete und daher vom Menschen unbewusst als ästhetischer Maßstab bei der Bewertung von Kunstwerken herangezogen werde. Dieser unbewusste Prozess gewinne umso mehr Bedeutung, je „naturnaher“, „unverbildeter“, und „volkstümlicher“ die Kunstwerke seien. Da Grimms Märchen bekanntlich direkt aus dem Munde des Volkes „abgelauscht sind“, sei es kein Wunder, dass hier der Goldene Schnitt als „natürliches Spannungsverhältnis“ in Erscheinung trete …[143] J. Benjafield und C. Davis schreiben dazu:
“Although the characters and situations depicted in fairy tales are often unrealistic, in the sense of being unlikely to be encountered in everyday life, the connotative structure of the characters is like that found in our impersonal environment. Since the stories are, in part, vehicles for teaching children about the general features of human nature, this correspondence makes perfectly good sense.”
„Obwohl die in den Märchen dargestellten Figuren und Situationen oft unrealistisch sind, das heißt im Alltag nicht vorkommen, entspricht die Bedeutungsstruktur der Figuren der unserer unpersönlichen Umwelt. Da die Märchen zum Teil dazu dienen, Kinder über die allgemeinen Merkmale der menschlichen Natur zu unterrichten, ist diese Entsprechung durchaus sinnvoll.“
Nach Meinung Benjafields und Davis erkläre dies auch das Auftreten des Goldenen Schnitts in der Musik Béla Bartóks – ein Beleg dafür, dass Bartóks Musik sich in vielerlei Hinsicht aus der Volksmusik speise.
Der Goldene Schnitt wurde auch in einem späten Gedicht Friedrich Hölderlins nachgewiesen. ln seinen letzten Lebenstagen, entweder im Mai oder Juni des Jahres 1843, schrieb Hölderlin in Tübingen Die Aussicht:
Wenn in die Ferne geht der Menschen wohnend Leben,
Wo in die Ferne sich erglänzt die Zeit der Reben,
Ist auch dabei des Sommers leer Gefilde,
Der Wald erscheint mit seinem dunklen Bilde;
Daß die Natur ergänzt das Bild der Zeiten,
Daß die verweilt, sie schnell vorübergleiten,
Ist aus Vollkommenheit, des Himmels Höhe glänzet
Den Menschen dann, wie Baume Blüth' umkränzet.
– Die Aussicht, Friedrich Hölderlin[145]
Roman Jakobson und Grete Lübbe-Grothues entdeckten, dass dieses Gedicht mit Hilfe des Goldenen Schnitts, genauer gesagt aus den Verhältnissen 8 : 5, 5 : 3 und 3 : 2, aufgebaut wurde.[146] Hierzu schreiben sie:
„Der goldene Schnitt (8:5 = 5:3) stellt zwei ungleiche Teile eines achtzeiligen Ganzen einander gegenüber und zerlegt Die Aussicht in zwei syntaktisch gleichmäßige Gruppen von fünf Verbafinita bzw. fünf Elementarsätzen (clauses), mit einer spiegelsymmetrischen Verteilung der Verben in den Halbversen des fünfzeiligen Major (3:2) und des dreizeiligen Minor (2:3).“
Die Frage, ob Hölderlin die Ästhetik des Goldenen Schnitts bewusst einsetzte, sei hier jedoch besonders schwierig zu beantworten, da Hölderlin bekanntlich in seinen letzten Lebensjahren stark an einer seelischen Krankheit litt. Immerhin gibt es nach Jakobson auffallende Anzeigen einer komplexen und zielbewussten Gestaltung und Vieles deute auf eine bewusste Verwendung der Verhältnisse 8 : 5, 5 : 3 und 3 : 2 hin.
Akustik und Musik[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt tritt innerhalb der Musik in zwei Rollen auf. Zum einen können die Frequenzen zweier Töne ein Goldenes Verhältnis haben. Andererseits kann die Komposition eines Stückes aus Teilen bestehen, deren Längen sich verhalten wie der Goldene Schnitt.
Frequenzverhältnisse[Bearbeiten | Quelltext bearbeiten]
Stehen die Frequenzen zweier Töne im Verhältnis der Fibonacci-Zahlen 8 : 5 (oder 5 : 8), so bildet sich als Klang eine kleine Sexte. Die Differenz des Verhältnisses 8 : 5 (= 1,6) zum Goldenen Schnitt (= 1,618…) sei so gering, dass, wie Rudolf Haase behauptet, der Goldene Schnitt selbstverständlich in den Zurechthörbereich der kleinen Sexte fällt. Haases Vorstellung ist also die, dass der Reiz der kleinen Sexte darin begründet ist, dass die Frequenzen ihrer Einzeltöne im Goldenen Verhältnis stehen, und dass das einfache Verhältnis 8 : 5 nur eine Annäherung daran ist.[148]
Komposition[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt wird gelegentlich in Strukturkonzepten von Musikstücken vermutet. So hat der ungarische Musikwissenschaftler Ernő Lendvai versucht, den Goldenen Schnitt als wesentliches Gestaltungsprinzip der Werke Béla Bartóks nachzuweisen. Seiner Ansicht nach hat Bartók den Aufbau seiner Kompositionen so gestaltet, dass die Anzahl der Takte in einzelnen Formabschnitten Verhältnisse bilden, die den Goldenen Schnitt approximieren würden. Allerdings sind seine Berechnungen umstritten.[149]
In der Musik nach 1945 finden sich Beispiele für die bewusste Proportionierung nach den Zahlen der Fibonacci-Folge, etwa im Klavierstück IX von Karlheinz Stockhausen oder in der Spektralmusik von Gérard Grisey.[150]
Instrumentenbau[Bearbeiten | Quelltext bearbeiten]
Der Goldene Schnitt wird gelegentlich im Musikinstrumentenbau verwendet. Insbesondere beim Geigenbau soll er für besonders klangschöne Instrumente bürgen. So wird behauptet, dass der berühmte Geigenbauer Stradivari den Goldenen Schnitt verwendete, um die klanglich optimale Position der F-Löcher für seine Violinen zu berechnen. Diese Behauptungen basieren jedoch lediglich auf nachträglichen numerischen Analysen von Stradivaris Instrumenten. Ein Nachweis, dass Stradivari bewusst den Goldenen Schnitt zur Bestimmung ihrer Proportionen angewandt habe, existiert jedoch nicht.[151][152]
Verwendung in Informatik und Numerik[Bearbeiten | Quelltext bearbeiten]
Datenstrukturen[Bearbeiten | Quelltext bearbeiten]
In der Informatik werden Daten in Hashtabellen gespeichert, um darauf schnell zuzugreifen. Die Position , an der ein Datensatz in der Tabelle gespeichert wird, berechnet sich durch eine Hashfunktion . Für einen effizienten Zugriff müssen die Datensätze möglichst gleichmäßig verteilt in die Tabelle geschrieben werden. Eine Variante für die Hashfunktion ist die multiplikative Methode, bei der die Hashwerte für eine Tabelle der Größe nach der folgenden Formel berechnet werden:
Dabei stellen Gaußklammern dar, die den Klammerinhalt auf die nächste ganze Zahl abrunden. Der Informatiker Donald E. Knuth schlägt für die frei wählbare Konstante vor, um eine gute Verteilung der Datensätze zu erhalten.[153]
Verfahren des Goldenen Schnittes[Bearbeiten | Quelltext bearbeiten]
Das Verfahren des Goldenen Schnittes (auch: Goldener-Schnitt-Verfahren,[154] Methode des Goldenen Schnittes oder Suchverfahren Goldener Schnitt) ist ein Verfahren der mathematischen nichtlinearen Optimierung, genauer berechnet es algorithmisch eine numerische Näherung für eine Extremstelle (Minimum oder Maximum) einer reellen Funktion einer Variablen in einem Suchintervall . Es basiert auf der analytischen Anwendung der ursprünglich geometrisch definierten stetigen Teilung. Im Gegensatz zum Intervallhalbierungsverfahren wird dabei das Suchintervall nicht bei jedem Schritt halbiert, sondern nach dem Prinzip des Goldenen Schnittes verkleinert. Der verwendete Parameter (tau) hat dabei nicht, wie bei dem allgemeineren Bisektionsverfahren, den Wert , sondern es wird gewählt, sodass sich zwei Punkte und für das Optimierungsverfahren ergeben, die das Suchintervall im Goldenen Schnitt teilen.[155]
Wird angenommen, dass jeder Punkt in jedem Intervall mit gleicher Wahrscheinlichkeit Extrempunkt sein kann, führt dies bei Unbestimmtheitsintervallen dazu, dass das Verfahren des Goldenen Schnittes um 14 % effektiver ist als die Intervallhalbierungsmethode. Im Vergleich zu diesem und weiteren sequentiellen Verfahren ist es – mathematisch gesehen – das für allgemeine Funktionen effektivste Verfahren; nur im Fall differenzierbarer Funktionen ist es der direkten mathematischen Lösung unterlegen.[156] Dass sich dieses Verfahren in der manuellen Rechnung nicht durchgesetzt hat, liegt vor allem an den notwendigen Wurzelberechnungen für die einzelnen Zwischenschritte.
Anzahl benötigter Divisionen im euklidischen Algorithmus[Bearbeiten | Quelltext bearbeiten]
Der klassische euklidische Algorithmus berechnet den größten gemeinsamen Teiler zweier natürlicher Zahlen und . Dabei müssen einige Divisionen durchgeführt werden. Je nach Beschaffenheit dieser Zahlen können aber mal mehr oder mal weniger Schritte erforderlich sein. Ist etwa , so endet der Algorithmus nach nur einem Schritt, egal wie groß diese Zahlen sind. Der Goldene Schnitt taucht in der anderen Richtung auf, nämlich beschreibt er die Anzahl der Schritte für die Fälle, in denen ganz besonders viele Divisionen gebraucht werden (worst case analysis). Bezeichnet die Anzahl der benötigten Divisionen, und , wobei zufällig ausgewählt werden, so gilt
- .
Dies zeigt, dass der euklidische Algorithmus selbst in der schlechtest möglichen Situation immer noch (nur) logarithmische Laufzeit besitzt.[157]
Auffälligkeit[Bearbeiten | Quelltext bearbeiten]
Eine weitere Verbindung zwischen der Informationstheorie und dem Goldenen Schnitt wurde durch Helmar Frank mit der Definition der Auffälligkeit hergestellt. Er konnte zeigen, dass der mathematische Wert des Maximums der Auffälligkeit sehr nah an das Verhältnis des Goldenen Schnitts herankommt.[158]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Goldenes Rechteck
- Zehneck
- Fünfzehneck
- Zwanzigeck
- Vierzigeck
- Vesica piscis
- Bronzener Schnitt
- Liste besonderer Zahlen
- Liste mathematischer Konstanten
Literatur[Bearbeiten | Quelltext bearbeiten]
Historische Literatur[Bearbeiten | Quelltext bearbeiten]
- Luca Pacioli; Constantin Winterberg (Hrsg. und Übers.): De divina proportione. Venedig 1509 / Carl Graeser, Wien 1889 (im Internet-Archiv: Online, bei alo: literature.at/alo).
- Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers. Rudolph Weigel, Leipzig 1854; archive.org.
- Adolf Zeising: Das Normalverhältniss der chemischen und morphologischen Proportionen. Rudolph Weigel, Leipzig 1856; archive.org.
- Gustav Theodor Fechner: Zur experimentalen Ästhetik. Hirzel, Leipzig 1871.
Neuere Literatur[Bearbeiten | Quelltext bearbeiten]
- Lieselotte Kugler, Oliver Götze (Hrsg.): Göttlich Golden Genial. Weltformel Goldener Schnitt? Hirmer, München 2016, ISBN 978-3-7774-2689-1, siehe hierzu: Portal Kunstgeschichte
- Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1996, ISBN 3-86025-404-9.
- Priya Hemenway: Divine Proportion. Phi in Art, Nature and Science. Sterling, New York 2005, ISBN 1-4027-3522-7. (Priya Hemenway: Der Geheime Code: Die rätselhafte Formel, die Kunst, Natur und Wissenschaft bestimmt. Taschen Verlag, Köln 2008, ISBN 978-3-8365-0708-0.)
- Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, New York 1998, ISBN 0-486-40007-7.
- Jürgen Fredel: Maßästhetik. Studien zu Proportionsfragen und zum Goldenen Schnitt. Lit, Hamburg 1998, ISBN 3-8258-3408-5.
- Albert van der Schoot: Die Geschichte des goldenen Schnitts. Aufstieg und Fall der göttlichen Proportion. Frommann-Holzboog, Stuttgart 2005, ISBN 3-7728-2218-5.
- Susanne Deicher: Rezension von: Albert van der Schoot: Die Geschichte des goldenen Schnitts. In: sehepunkte 5, 15. Dezember 2005, Nr. 12, Weblink.
- Hans Walser: Der Goldene Schnitt. Teubner, Stuttgart 1993, ISBN 3-8154-2511-5.
- Georg Markowsky: Misconceptions about the Golden Mean (PDF; 2,1 MB). In: The College Mathematics Journal, Band 23, Ausgabe 1, Januar 1992.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Deutsch
- Marcus Frings: Goldener Schnitt. In: RDK. Labor (2015).
Englisch
- Marcus Frings: The Golden Section in Architectural Theory. In: Nexus Network Journal, 2002, 4/1.
- Eric W. Weisstein: Golden Ratio. In: MathWorld (englisch).
- John J. O’Connor, Edmund F. Robertson: The Golden Ratio. In: MacTutor History of Mathematics archive (englisch).
- Alexander Bogomolny: Golden Ratio. cut-the-knot.org
- Steven Strogatz: Proportion Control. New York Times (Online), 24. September 2012.
- Folge A001622 in OEIS (Dezimalentwicklung von ), Folge A028259 in OEIS (Engel-Entwicklung von ), Folge A118242 in OEIS (Pierce-Entwicklung von ).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 16.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 18.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 18–20.
- ↑ a b c August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, V. Abschnitt, Aufgaben ersten und zweiten Grades., §32. Graphische Auflösung der Gleichungen zweiten Grades., S. 175–176, Fig. 137., S. 188–189 (Textarchiv – Internet Archive).
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 10, 15.
- ↑ Rudolf Haller: Elemente des Euklid. Edition Opera Platonis 2010, Buch II, Satz 11 (PDF; 209 KB).
- ↑ Leonardo da Pisa: Liber abbaci. (Cap. I, 7, dort unter anderen Aufgaben: Quot paria coniculorum in uno anno ex uno pario germinentur), hrsg. von Baldassare Boncompagni, Scritti di Leonardo Pisano matematico del secolo decimoterzo. Band I, Tipografia delle scienze matematiche e fisiche, Rom 1857, S. 283 f., Wiedergabe der Handschrift Florenz, Cod. magliabechiano cs cI, 2626, fol. 123v–124r, bei Heinz Lüneburg: Leonardi Pisani Liber Abbaci oder Lesevergnügen eines Mathematikers. 2., überarb. und erw. Ausgabe. BI Wissenschaftsverlag, Mannheim u. a. 1993, ISBN 3-411-15462-4, nach S. 252; Wiedergabe des lateinischen Textes der Kaninchenaufgabe u. a. bei Bernd Thaller: Leonardo und der Goldene Schnitt (PDF; 3 MB). 30. Juni 2017.
- ↑ Formalisierte Wiedergabe nach Heinz Lüneburg: Leonardi Pisani Liber Abbaci oder Lesevergnügen eines Mathematikers. 2., überarb. und erw. Ausgabe. BI Wissenschaftsverlag, Mannheim u. a. 1993, ISBN 3-411-15462-4, S. 298.
- ↑ Leonardo da Pisa: Liber abbaci. Cap. 15, ed. Boncompagni S. 438, zu finden schon in der Wiedergabe von cap. 15 bei Guillaume Libri: Histoire des sciences mathématiques in Italie. Band II, Paris: Jules Renouard et C.ie, 1838, S. 430 (Auszug in der Google-Buchsuche).
- ↑ Leonard Curchin, Roger Herz-Fischler: De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrême et moyenne raison? (PDF) In: Centaurus. Roger Herz-Fischler, 1985, abgerufen am 3. Oktober 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 10.
- ↑ Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, Minneola (New York) 1998, S. 158 (Section 31.J.iii).
- ↑ Allgemeine deutsche Real-Enzyklopädie für die gebildeten Stände. In zehn Bänden. Vierter Band (G und H). Fünfte Original-Ausgabe. F. A. Brockhaus, Leipzig 1819, S. 296.
- ↑ Otfried Lieberknecht: First occurrence of the term “Goldener Schnitt”/“sectio aurea”. (PDF) E-Mail-Korrespondenz. Herz-Fischler, 19. Mai 2018, S. 1–4, abgerufen am 1. Oktober 2022.
- ↑ M. Johann Wentzel Kaschube: Cursus mathematicus, Oder Deutlicher Begrief Der Mathematischen Wissenschaften. Johann Felix Bielcke, Jena 1717 (Digitalisat [Google]).
- ↑ a b M. Johann Wentzel Kaschube: Cursus mathematicus, Oder Deutlicher Begrief Der Mathematischen Wissenschaften. Johann Felix Bielcke, Jena 1717, S. 566 (Digitalisat [Google]).}
- ↑ a b c d Ernst Florens Friedrich Chladni: Die Akustik. Breitkopf und Härtel, Leipzig 1802 (eingeschränkte Vorschau in der Google-Buchsuche), S. 33, abgerufen am 1. Oktober 2022.
- ↑ Gottfried Wilhelm Leibniz, Anmerkungen Christian Kortholt: Viri illustris Godefridi Guil. Leibnitii epistolae ad diversos … Hrsg.: Christian Kortholt. Band 1. Bern. Christoph Breitkopf, Leipzig 1734, S. 241 f., Brief 154 (Latein, Titelblatt, S. 242 [Google]).
- ↑ Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers, […]. Verlag Rudolph Weigel, Leipzig 1854, S. 159 (abgerufen am 18. Oktober 2022).
- ↑ a b Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers, […]. Verlag Rudolph Weigel, Leipzig 1854, S. 163 (abgerufen am 3. Oktober 2022).
- ↑ Gustav Theodor Fechner: Vorschule der aesthetik. Breitkopf & Härtel, 1876, S. 190.
- ↑ Camillo Sitte: Über den praktischen Wert der Lehre vom Goldenen Schnitt. In: Camillo Sitte: Schriften zu Kunsttheorie und Kunstgeschichte. Böhlau 2010, ISBN 978-3-205-78458-6, S. 435–446, besonders 438–439 (Auszug (Google)).
- ↑ Underwood Dudley: Die Macht der Zahl: Was die Numerologie uns weismachen will. Gabler, 1999, ISBN 3-7643-5978-1, S. 243–245 (Auszug (Google)).
- ↑ a b The Nobel Prize in Chemistry 2011. Nobelprize.org (offizielle Homepage des Nobelpreises), abgerufen am 22. März 2023 (englisch). Siehe Interview.
- ↑ a b Elisa Wheeler: Den Goldenen Schnitt gibt es auch in der Quantenwelt. Verborgene Symmetrie im Strukturaufbau von fester Materie nachgewiesen. Helmholtz-Zentrum Berlin, 1. Juli 2010, S. 1–2, abgerufen am 6. Dezember 2022.
- ↑ Bronstein, Semendjajew, et al.: Taschenbuch der Mathematik. 6. Auflage. Verlag Harri Deutsch, S. 2.
- ↑ Folge A001622 in OEIS.
- ↑ Alexander J. Yee: Records Set by y-cruncher. In: numberworld.org, abgerufen am 27. Oktober 2022 (englisch).
- ↑ Ivan Niven: Irrational numbers, The Mathematical Association of America, Wiley and Sons, 1956, S. 15–16.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, Band 94). Cambridge University Press, 1.2 The Golden Mean, φ, 2003, S. 6.
- ↑ Herbert Henning, Christian Hartfeldt: 16 Die Fibonacci-Zahlen. Goldener Schnitt in der Mathematik. (PDF) Universität Magdeburg, 2003, S. 19, abgerufen am 4. Oktober 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 87–91
- ↑ Manfred Schroeder: Number Theory in Science and Communication. 5. Auflage. Springer, S. 91.
- ↑ Manfred Schroeder: Number Theory in Science and Communication. 5. Auflage. Springer, S. 84.
- ↑ Ivan Niven: Irrational numbers, The Mathematical Association of America, Wiley and Sons, 1956, S. 68.
- ↑ Ivan Niven: Irrational numbers, The Mathematical Association of America, Wiley and Sons, 1956, S. 70.
- ↑ Ben Green: Irrational and Transcendental Numbers. In: Timothy Gowers, June Barrow-Green, Imre Leader: The Princeton Companion to Mathematics. Princeton University Press 2008, ISBN 978-0-691-11880-2, S. 222 (Auszug (Google)).
- ↑ Peter Berger: Der goldene Schnitt. (PDF) S. 14, abgerufen am 28. August 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 101.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 101.
- ↑ Manfred Schroeder: Number Theory in Science and Communication. 5. Auflage. Springer, S. 79.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage. Verlag Harri Deutsch, S. 198.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 21.
- ↑ Johann Friedrich Lorenz: Euklids Elemente, fünfzehn Bücher. Hrsg.: Im Verlag der Buchhandlung des Waysenhauses. Halle 1781, S. 31 ff. (Euklids Elemente, Zweytes Buch, Der 11. Satz. Eine gegebne gerade Linie, AB, so zu schneiden … [abgerufen am 19. Dezember 2016]).
- ↑ Forum Geometricorum Volume 5 (2005) 135–136. (PDF; 26 kB).
- ↑ Euklid: XIII.9. (PDF) Euklid: Stoicheia. Buch XIII. Opera Platonia, 2010, S. 9–10, abgerufen am 24. Oktober 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 22–23.
- ↑ John Stillwell: Mathematics and Its History. Third Edition. Springer, S. 28.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 44–45.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 80–84.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt, zweite, überarbeitete und erweiterte Auflage, Spektrum Akademischer Verlag, Heidelberg/Berlin/Oxford 1996, ISBN 978-3-8154-2511-4, Seiten 73 und 74.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt, zweite überarbeitete und erweiterte Auflage, Spektrum Akademischer Verlag, Heidelberg/Berlin/Oxford 1996, ISBN 978-3-8154-2511-4, Seiten 22 und 23.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt, zweite überarbeitete und erweiterte Auflage, Spektrum Akademischer Verlag, Heidelberg/Berlin/Oxford 1996, ISBN 978-3-8154-2511-4, Seiten 67 und 68.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 51.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 53.
- ↑ Alfred Posamentier, Ingmar Lehmann: The Glorious Golden Ratio, Prometheus Books, S. 128.
- ↑ Stanisław Świerczkowski: On successive settings of an arc on the circumference of a circle. In: Fundamenta Mathematicae. 46.2, 1958, S. 187–189.
- ↑ Tony van Ravenstein: Optimal Spacing of Points on a Circle. In: The Fibonacci Quaterly. 27, 1989, S. 18–24, mathstat.dal.ca (PDF; 1,6 MB).
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 57–61.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 60.
- ↑ Forum Geometricorum Volume 16 (2016) 429–430 (PDF).
- ↑ a b c d Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 62.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 63.
- ↑ I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik. 20. Auflage. Gemeinschaftsausgabe Verlag Nauka Moskau und BSB B.G. Teubner Verlagsgesellschaft, Leipzig 1981, S. 167.
- ↑ Daniel Lordick: 6 Torusknoten, Torusverschlingungen, Zöpfe und Papierbänder. Von der Knotentheorie zum Klettergerüst. researchgate.net, Februar 2012, S. 67–11, abgerufen am 25. April 2023.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 39–44.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 40.
- ↑ a b c Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 41.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 42–44.
- ↑ Frazer Jarvis: Algebraic Number Theory. Springer, S. 131.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer, 1992, S. 16.
- ↑ a b c Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2 The Golden Mean, φ, Band 94). Cambridge University Press, 2003, S. 7.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, Well-Known Constants, Band 94). Cambridge University Press, 2003, S. 8.
- ↑ Alfred Posamentier, Ingmar Lehmann: The Glorious Golden Ratio. Prometheus Books, S. 75.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.4.1 Infinite Series, Band 94). Cambridge University Press, 2003, S. 20.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2 The Golden Mean, φ, Band 94). Cambridge University Press, 2003, S. 7–8.
- ↑ Bruce Berndt: Ramanujan’s Notebook Part III. Springer, S. 83–84.
- ↑ Steven R. Finch: Mathematical Constants, 1.8 Khintchine–Lévy Constants (= Encyclopedia of Mathematics and its Applications. Band 94). Cambridge University Press, 2003, S. 59–62.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, Well-Known Constants, Band 94). Cambridge University Press, 2003, S. 62.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 2.16.3 Alternating Bit Sets, Band 94). Cambridge University Press, 2003, S. 148.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 2.16 Stolarsky–Harborth Constant, Band 94). Cambridge University Press, 2003, S. 149.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.5.4 Gamma Function, Band 94). Cambridge University Press, 2003, S. 33.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, Well-Known Constants, Band 94). Cambridge University Press, 2003, S. 44.
- ↑ Eric Weisstein: Silver Ratio. WolframMathWorld, 11. Januar 2021, abgerufen am 11. Oktober 2022.
- ↑ Dario Jotanovic: 9.1 Silberner Schnitt. (PDF) In: Der Goldene Schnitt Implementierung mathematischer Algorithmen. Hochschule Darmstadt, S. 27, archiviert vom (nicht mehr online verfügbar); abgerufen am 11. Oktober 2022.
- ↑ a b c Ephraim Salomon Unger: Praktische Uebungen für angehende Mathematiker, Band 1: Das Berechnen, Verwandeln und Theilen der Figuren. F .A. Brockhaus, Leipzig 1828, Abschnitt Vermischte Aufgaben, S. 205–206 (Digitalisat S. 205 [Google]).
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2.1 Analysis of a Radical Expansion , Band 94). Cambridge University Press, 2003, S. 8–9.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2 The Golden Mean, φ , Band 94). Cambridge University Press, 2003, S. 9.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.1.1 Generalized Continued Fractions, Band 94). Cambridge University Press, 2003, S. 3.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2 The Golden Mean, φ, Band 94). Cambridge University Press, 2003, S. 9.
- ↑ D. Viswanadt: Random Fibonacci sequences and the number 1.13198824… In: Math. Comp. 69, 2000, S. 1131–1155.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 1.2.4 Random Fibonacci Sequences, Band 94). Cambridge University Press, 2003, S. 10.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 124.
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 123.
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 128.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 125.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 130–133.
- ↑ Siehe Dvorak/Freistetter/Kurths: Chaos and stability in planetary systems. (Springer Lecture Notes in Physics, 2006), S. 118–121 und den Wikipedia-Artikel über noble Zahlen.
- ↑ Remo Badii, A. Politi: Complexity: Hierarchical Structures and Scaling in Physics. Cambridge University Press, 1999, ISBN 0-521-66385-7, S. 46 (Auszug (Google)).
- ↑ Manfred Schroeder: Number Theory in Science and Communication. 5. Auflage. Springer, S. 80.
- ↑ Marcus Chown: The golden rule – It links art, music and even architecture. Marcus Chown on an enigmatic number. The Guardian, 16. Januar 2003, abgerufen am 31. Dezember 2013.
- ↑ J. A. Nieto: A Link Between Black Holes and the Golden Ratio. In: Cornell University. 2. Juni 2011, arxiv:1106.1600 (englisch).
- ↑ D. Shechtman, I. Blech, D. Gratias, J. W. Cahn: Metallic phase with long range orientational order and no translation symmetry. In: Physical Review Letters. Band 53(20), 1984, S. 1951–1954 (englisch, fu-berlin.de [PDF]).
- ↑ Horst Knietzsch: Film – gestern und heute: Gedanken und Daten zu 7 Jahrzehnten Geschichte der Filmkunst. Urania, Leipzig 1967, bei AbeBooks.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 26–29.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 26.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 27, Bild 1.11, Fig. 7.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 27, Bild 1.11, Fig. 6.
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt, zweite, überarbeitete und erweiterte Auflage, Spektrum Akademischer Verlag, Heidelberg/Berlin/Oxford 1996, ISBN 978-3-8154-2511-4, Seite 71.
- ↑ M. Johann Wentzel Kaschube: Cursus mathematicus, Oder Deutlicher Begrief Der Mathematischen Wissenschaften. Johann Felix Bielcke, Jena 1717, S. 564 (Digitalisat [Google]).}
- ↑ M. Johann Wentzel Kaschube: Cursus mathematicus, Oder Deutlicher Begrief Der Mathematischen Wissenschaften. Johann Felix Bielcke, Jena 1717, S. 539 (Digitalisat [Google] – Tab. I Alg.).
- ↑ a b c Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 74–76.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 158–160.
- ↑ Gábor Paál: Was ist schön? Die Ästhetik in allem. Königshausen & Neumann, 2020, ISBN 978-3-8260-7104-1, S. 304.
- ↑ Gustav Theodor Fechner: Vorschule der Ästhetik. (PDF) XIV. […] Experimentale Aesthetik. Goldner Schnitt und Quadrat. Breitkopf & Härtel, 1876, S. 192, abgerufen am 3. Oktober 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 136–137.
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 138.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 138–141.
- ↑ Website der Hochschule Augsburg, Thesenpapier zur Makro-Typografie Proportionen und Formate von Prof. Michael Wörgötter, Fakultät für Gestaltung (PDF-Download).
- ↑ Rik Verhulst: Im Banne der Mathematik – Die kulturellen Aspekte der Mathematik in Zivilisation, Kunst und Natur. Springer Spektrum, Springer-Verlag GmbH, Berlin 2019, ISBN 978-3-662-58797-3, S. 307.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 17.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 142–147.
- ↑ Mario Livio: The golden ratio: The story of phi, the world’s most astonishing number. Broadway Books, 2003, ISBN 0-7679-0816-3, S. 177–178.
- ↑ Alfred Posamentier, Ingmar Lehmann: The Glorious Golden Ratio, Prometheus Books, S. 335.
- ↑ Mario Livio: The golden ratio: The story of phi, the world’s most astonishing number. Broadway Books, 2003, ISBN 0-7679-0816-3, S. 5.
- ↑ a b Robert L. Herbert, Georges Seurat, 1859–1891, The Metropolitan Museum of Art, 1991, S. 316.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 148–155.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 157.
- ↑ Herbert Henning, Christian Hartfeldt: Das Lächeln der Mona Lisa Fakultät für Mathematik der Otto-von-Guericke-Universität Magdeburg, PDF-Präsentation, Seite 49 (aus dem Artikel: Vom Lächeln der Mona Lisa und der Schönheit einer Sonnenblume in: Der Mathematikunterricht, 53 (2007), Nr. 1/2, Seite 93–102).
- ↑ The Fibonacci Sequence – The Mona Lisa. Auf: thefibonaccisequence.weebly.com, abgerufen am 5. Oktober 2022.
- ↑ Fiona Grießhammer, Rebekka Maas: Fibonacci-Zahlen und der Goldene Schnitt. Aus den Seminarthemen der Fakultät für Mathematik und Informatik der Universität Leipzig (PDF, S. 43).
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 157–158.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 159.
- ↑ Louis Hautecoeur: Georges Seurat. Schuler Verlagsgesellschaft, München 1974, ISBN 3-7796-5030-4, S. 69 und 70.
- ↑ Michael Frye: Digitale Landschaftsfotografie: Fotografieren wie Ansel Adams und Co. Hüthig Jehle Rehm, 2010, ISBN 978-3-8266-5896-9, S. 72 (Auszug (Google)).
- ↑ Garry Reynolds: Zen oder die Kunst der Präsentation: mit einfachen Ideen gestalten und präsentieren. Pearson Education 2008, ISBN 978-3-8273-2708-6, S. 151–152 (Auszug (Google)).
- ↑ Mechthild Haas: Palermo oder die Vermessbarkeit der Welt. Blinky Palermo. Hrsg.: Hessisches Landesmuseum Darmstadt. Hessisches Landesmuseum, Darmstadt 2006, ISBN 3-926527-79-X, S. 22 und 24.
- ↑ Thomas Micchelli: A Struggle for Balance. 10. September 2016, abgerufen am 12. Januar 2017.
- ↑ Udo Hebisch: Mathematik und Kunst. Bilder im virtuellen Mathe-Museum der TU Freiberg. Technische Universität Bergakademie Freiberg, 2008, abgerufen am 15. Oktober 2022.
- ↑ Udo Hebisch: Der goldene Schnitt. Bilder im virtuellen Mathe-Museum der TU Freiberg. Technische Universität Bergakademie Freiberg, 2009, abgerufen am 15. Oktober 2022.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 164.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 165.
- ↑ a b Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 165–166.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 166.
- ↑ Grete Lübbe-Grothues: Grammatik und Idee in den Scardanelli-Gedichten Hölderlins. (PDFf) Die Aussicht (Nr. 48). Philosophisches Jahrbuch, S. 89–90, abgerufen am 11. Juli 2023.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 166–167.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 167.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. 2., überarbeitete und erweiterte Auflage. Spektrum Akademischer Verlag, 1996, S. 168.
- ↑ Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1988, ISBN 3-411-03155-7, S. 165–167.
- ↑ Jonathan Kramer: The Fibonacci Series in Twentieth-Century Music. In: Journal of Music Theory. Band 17, Nr. 1, 1973, S. 110–148.
- ↑ How a Violin is Made. In: Popular Mechanics. September 1943, S. 106–108; Textarchiv – Internet Archive.
- ↑ Stewart Pollens: Stradivari. Cambridge University Press, 2010, ISBN 978-0-521-87304-8, S. 239 (Auszug (Google)).
- ↑ Thomas H. Cormen, Charles Leiserson, Ronald Linn Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, 2001, ISBN 0-262-53196-8, S. 231–232.
- ↑ Markos Papageorgiou, Marion Leibold, Martin Buss: Optimierung. 4. Auflage. Springer-Verlag, Berlin/Heidelberg 2015, S. 30, doi:10.1007/978-3-662-46936-1.
- ↑ Florian Jarre, Josef Stoer: Optimierung. Springer, Berlin 2004, ISBN 3-540-43575-1, S. 130 ff. (Auszug (Google)).
- ↑ W. Gellert u. a.: Kleine Enzyklopädie Mathematik. VEB Bibliographisches Institut Leipzig, 1979, S. 694.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications, 2.18 Porter–Hensley Constants, Band 94). Cambridge University Press, 2003, S. 156–159.
- ↑ Horst Völz: Computer und Kunst (= Reihe Akzent, Band 87). 2. Auflage. Urania Verlag, Leipzig, Jena, Berlin 1990 (ComputerKunst.doc 11.11.06; PDF; 8,7 MB), Abschnitt Der Überraschungswert, S. 14 f. (abgerufen am 13. August 2018).

























































































































































































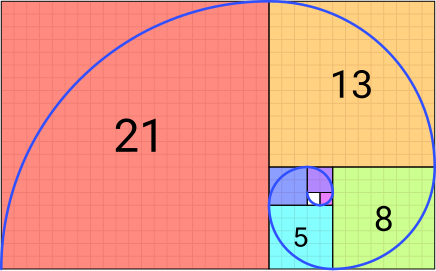



































![{\displaystyle {\bar {x}}_{\text{geom}}={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsm x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8218f179881c3afe5663221e4b86c0c60bdd94b0)
![{\displaystyle x={\sqrt[{2}]{a(a-x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e155c4db85203c7f8d4366d8030b50851e8d6085)






































































































![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{|c_{1}\cdots c_{n}|}}=\left({\frac {5\Phi +3}{5\Phi +2}}\right)^{\frac {\log(2)}{\log(\Phi )}}\prod _{k=1}^{\infty }\left({\frac {8(k-1)\Phi +(2k-3)^{2}+4}{8(k-1)\Phi +(2k-3)^{2}}}\right)^{\frac {\log(k)}{\log(\Phi )}}=5{,}4545172445\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ea81bcea3cd3bd404a2564498e10a642e07b5e8)

![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{|Q_{n}|}}=e^{\frac {\pi ^{2}}{12\log(\Phi )}}=5{,}5243079702\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8cb84a9d75ca3274b4a8846d9bd864a9ca2c57e)
























































![{\displaystyle \psi ={\sqrt[{3}]{{\tfrac {1}{2}}+{\tfrac {\sqrt {69}}{18}}}}+{\frac {1}{3{\sqrt[{3}]{{\tfrac {1}{2}}+{\tfrac {\sqrt {69}}{18}}}}}}=1{,}3247\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cfad2fb5288252e441ed02c8fec00d5d49607a3)

![{\displaystyle \psi ={\sqrt[{3}]{1+{\sqrt[{3}]{1+{\sqrt[{3}]{1+\cdots }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92b339fb403a0a451e40d57070a43e6f959458)




![{\displaystyle \lim _{n\to \infty }{\frac {h_{n+1}}{h_{n}}}=\chi ={\sqrt[{3}]{{\tfrac {19}{27}}+{\tfrac {\sqrt {33}}{9}}}}+{\frac {4}{9{\sqrt[{3}]{{\tfrac {19}{27}}+{\tfrac {\sqrt {33}}{9}}}}}}=1{,}8392\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb64d64c349b6df988e4367860ccde30b7883717)










![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{|x_{n}|}}=1{,}13198824\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0ffd4b1e3a85e569cb57818cb2aac4ba1f5f5b9)

















































































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









