Mohrscher Spannungskreis

Abb. 1: Mohr’scher Spannungskreis im Spannungsraum mit Normalspannungen σ_n auf der Abszisse und Schubspannungen σ_t auf der Ordinate

Mohr’sche Spannungskreis oder kurz Mohr’sche Kreis, benannt nach Christian Otto Mohr, ist eine Möglichkeit, den 2D-Spannungszustand in einem Punkt eines Körpers zu veranschaulichen oder zu untersuchen, siehe Abbildung 1.

Seine Gleichung lautet im Spannungsraum, wo auf der Abszisse die Normalspannungen und auf der Ordinate die Schubspannungen aufgetragen sind:

${\mathsf {(\sigma _{uu,vv}-M)^{2}+\sigma _{uv}^{2}=R^{2}}}$

mit

${\mathsf {M}}={\mathsf {{\frac {1}{2}}(\sigma _{xx}+\sigma _{yy})}}$   und   ${\mathsf {R}}={\mathsf {\sqrt {{\frac {1}{4}}(\sigma _{xx}-\sigma _{yy})^{2}+\sigma _{xy}^{2}}}}$

Darin ist

• {σ_xx, σ_yy, σ_xy} ein gegebener Spannungszustand in der xy-Ebene, die zu einer Hauptspannungsrichtung senkrecht ist, wie zum Beispiel im ebenen Spannungszustand,
• {σ_uu, σ_vv, σ_uv} ist der Spannungszustand im uv-Koordinatensystem, dessen u- und v-Achsen wie in Abb. 2 um den Winkel α gegenüber den x- bzw. y-Achsen verdreht sind,
• M der Mittelpunkt des Kreises auf der Abszisse und
• R der Radius des Kreises.

Am Kreis kann abgelesen werden, in welchem Winkel β zur x-Achse die Hauptschubspannung τ_I und in welchem Winkel γ die Hauptspannungen σ_I,II auftreten.

Neben dem Cauchy-Spannungstensor können auch andere symmetrische Tensoren mit dem Mohr’schen Kreis veranschaulicht oder untersucht werden, z. B. der Verzerrungstensor und der Trägheitstensor. Neben dem Mohr’schen Kreis gibt es auch andere Verfahren zur Veranschaulichung symmetrischer Tensoren, z. B. Ellipsoide oder Superquadriken, je nachdem der Tensor positiv definit ist oder nicht.

Mohr führte den Spannungskreis 1882 ein.

Koordinatentransformation

Abb. 2: Spannungs­komponenten in zwei Koordinaten­systemen, die im Winkel α zueinander verdreht sind

Eine Koordinaten­trans­formation wird unter anderem bei einer Drehung wie im Bild notwendig, und wenn diese um eine Haupt­spannungs­richtung als Drehachse erfolgt, kann der Spannungszustand in der zur Drehachse senkrechten Ebene mit dem Mohr’schen Spannungskreis veranschaulicht werden. Allgemein geschieht eine Drehung mathematisch mit einem orthogonalen Tensor Q und die Koordinaten­trans­formation beim Spannungstensor σ gemäß σ’=Q·σ·Q^⊤, siehe Euklidische Transformation. In der Ebene bezüglich kartesischer Koordinaten der Abbildung kann das als Matrizengleichung mit Drehmatrizen und dem Sinus und Cosinus geschrieben werden:

${\mathsf {{\begin{pmatrix}{\mathsf {\sigma _{uu}}}&{\mathsf {\sigma _{uv}}}\\{\mathsf {\sigma _{uv}}}&{\mathsf {\sigma _{vv}}}\end{pmatrix}}={\begin{pmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{pmatrix}}\cdot {\begin{pmatrix}{\mathsf {\sigma _{xx}}}&{\mathsf {\sigma _{xy}}}\\{\mathsf {\sigma _{xy}}}&{\mathsf {\sigma _{yy}}}\end{pmatrix}}\cdot {\begin{pmatrix}\cos \alpha &\sin \alpha \\-\sin \alpha &\cos \alpha \end{pmatrix}}}}$

Die Komponenten in der uv-Ebene auf der linken Seite können mit den Additionstheoremen der Winkelfunktionen ausgerechnet werden:

${\begin{aligned}{\mathsf {\sigma _{uu}}}=&{\mathsf {\sigma _{xx}\cos ^{2}\alpha -2\sigma _{xy}\sin \alpha \,\cos \alpha +\sigma _{yy}\sin ^{2}\alpha }}\\=&{\mathsf {{\frac {1}{2}}(\sigma _{xx}+\sigma _{yy})+{\frac {1}{2}}(\sigma _{xx}-\sigma _{yy})\cos 2\alpha -\sigma _{xy}\sin 2\alpha }}\\{\mathsf {\sigma _{vv}}}=&{\mathsf {\sigma _{xx}\sin ^{2}\alpha +2\sigma _{xy}\cos \alpha \sin \alpha +\sigma _{yy}\cos ^{2}\alpha }}\\=&{\mathsf {{\frac {1}{2}}(\sigma _{xx}+\sigma _{yy})-{\frac {1}{2}}(\sigma _{xx}-\sigma _{yy})\cos 2\alpha +\sigma _{xy}\sin 2\alpha }}\\{\mathsf {\sigma _{uv}}}=&{\mathsf {\sigma _{xx}\sin \alpha \,\cos \alpha +(\cos ^{2}\alpha -\sin ^{2}\alpha )\sigma _{xy}-\sigma _{yy}\sin \alpha \,\cos \alpha }}\\=&{\mathsf {{\frac {1}{2}}(\sigma _{xx}-\sigma _{yy})\sin 2\alpha +\sigma _{xy}\cos 2\alpha }}\end{aligned}}$

Hier zeigt sich mit M=(σ_xx+σ_yy)/2:

${\mathsf {(\sigma _{uu}-M)^{2}=(\sigma _{vv}-M)^{2}=\left({\frac {1}{2}}(\sigma _{xx}-\sigma _{yy})\cos 2\alpha -\sigma _{xy}\sin 2\alpha \right)^{2}}}$

und

${\mathsf {(\sigma _{uu}-M)^{2}+\sigma _{uv}^{2}=(\sigma _{vv}-M)^{2}+\sigma _{uv}^{2}={\frac {1}{4}}(\sigma _{xx}-\sigma _{yy})^{2}+\sigma _{xy}^{2}=:R^{2}}}$

Letzteres ist die Gleichung des Mohr’schen Kreises in einem Koordinatensystem, in dem die Normalkomponenten σ_uu,vv auf der Abszisse und die Schubkomponenten σ_uv auf der Ordinate aufgetragen werden. Der Mittelpunkt des Kreises liegt auf der Abszisse bei M und sein Radius ist R.

Die folgenden Punkte sind von besonderem Interesse:

• Bei σ_uu=σ_vv=M ist die Schubkomponente σ_uv extremal, also gleich der Hauptschubspannung, und der Winkel β im Bild errechnet sich aus seinem Tangens gemäß ${\mathsf {\tan 2\beta ={\tfrac {\sigma _{xx}-\sigma _{yy}}{2\sigma _{xy}}}}}$
• Bei σ_uv=0 sind die Normalkomponenten extremal, also gleich den Hauptspannungen σ_I,II in der Ebene. Die Hauptspannungen stellen sich im Winkel γ oder γ±90° ein mit ${\mathsf {\tan 2\gamma ={\tfrac {2\sigma _{xy}}{\sigma _{yy}-\sigma _{xx}}}=-{\tfrac {1}{\tan 2\beta }}}}$.

Der Kehrwert des Tangens von 2β gehört zum Ergänzungswinkel 90°−2β=2γ, worin sich zeigt, dass die Hauptschubspannung im 45°-Winkel zu den Hauptspannungen auftritt.

Der Radius ist eine Invariante, denn

${\begin{aligned}{\mathsf {\sigma _{uu}+\sigma _{vv}}}=&{\mathsf {\sigma _{xx}+\sigma _{yy}}}\\{\mathsf {\sigma _{uu}\sigma _{vv}-\sigma _{uv}^{2}}}=&{\mathsf {\sigma _{xx}\sigma _{yy}-\sigma _{xy}^{2}}}\\{\mathsf {R^{2}}}=&{\mathsf {{\frac {1}{4}}[(\sigma _{xx}+\sigma _{yy})^{2}-4(\sigma _{xx}\sigma _{yy}-\sigma _{xy}^{2})]}}\end{aligned}}$

Die ersten beiden Größen entsprechen den Hauptinvarianten Spur und Determinante, weswegen auch der Radius R eine Invariante ist.

Die Situation im Bild entspricht den Zahlenwerten (die Einheiten werden der Übersichtlichkeit halber unterschlagen)

σ_xx=11, σ_yy=3, σ_xy=3, α=36,565°

Mit obigen Transformationsformeln berechnet sich in augenscheinlicher Übereinstimmung mit dem Bild auf vier signifikante Stellen gerundet:

σ_uu=5,290, σ_vv=8,710, σ_uv=4,698,

β=26,57°, τ_I=5

γ=-18,44°, σ_I=12

γ=71,57°, σ_II=2

Mohr'scher Spannungskreis und Schnittspannungsvektoren

Der Spannungs- oder Traktionsvektor t wird auf einem infinitesimalen Volumen durch einen Freischnitt sichtbar. Der Vektor wird zerlegt in seinen Anteil $\sigma _{n}$ (hier auch $t_{\bar {x}}$ bezeichnet) senkrecht zur Schnittfläche (den sogenannten Normalspannungsanteil) und seinen Anteil $\tau _{n}$ (hier auch $t_{\bar {y}}$ bezeichnet) parallel zur Schnittfläche (den so genannten Schubspannungsanteil). Abhängig vom Winkel $\varphi$, unter dem geschnitten wird, lassen sich Paare $(t_{\bar {x}},t_{\bar {y}})$ berechnen und in ein Diagramm als Punkte einzeichnen. Die Menge aller Punkte ist der Mohr’sche Kreis. An ihm lassen sich z. B. die Hauptspannungen, die Hauptspannungsrichtungen oder die größte Schubspannung ablesen. Dadurch gewinnt man eine anschauliche Vorstellung von der Beanspruchung des Volumens. Bei Festigkeitskriterien, wie Versagenskriterien, Fließkriterien oder Elastizitätsgrenzen, von isotropen, homogenen Materialien sind ausschließlich die Hauptspannungen relevant. Bei einigen Festigkeitskriterien ist nur die Beanspruchung in der Ebene der größten und kleinsten Hauptspannung relevant. Zu ihrer Beurteilung wird auch im Computerzeitalter oft der Mohr’sche Spannungskreis verwendet, denn er liefert schnell eine anschauliche Lösung.

Der Mohr’sche Kreis kann auch zur Berechnung des Traktionsvektors auf eine beliebige Flächennormale verwendet werden und somit kann man die Komponenten des Spannungstensors rückbestimmen: Sind die Spannungstensor-Komponenten bezogen auf ein kartesisches $(x,y)$-Koordinatensystem gegeben, dann lassen sich mit dem Mohr’schen Kreis die Spannungstensor-Komponenten bezogen auf ein kartesisches $({\bar {x}},{\bar {y}})$-Koordinatensystem grafisch bestimmen. Vorausgesetzt ist hierbei, dass das $({\bar {x}},{\bar {y}})$-Koordinatensystem durch eine Drehung um den Winkel $\varphi$ aus dem $(x,y)$-Koordinatensystem hervorgeht.

Schnittspannungsvektor

(x, y)-Komponenten

Teilchen mit Spannung $\sigma$ geschnitten senkrecht zu x (links) und unter einem Winkel $\varphi$ (rechts), Normalen-Einheits­vektor n, Schnitt­spannungs­vektor t

Der Spannungszustand an einem Teilchen ist festgelegt durch den symmetrischen Cauchy-Spannungstensor $\sigma$, der meist als (2,0)-Tensor definiert wird. An diesem Teilchen und durch seine unmittelbare Umgebung lässt sich ein Freischnitt führen in beliebiger Richtung. An der entstandenen Schnittfläche lässt sich der Schnittspannungsvektor t (traction vector) berechnen. Der Zusammenhang zwischen dem Spannungstensor und dem Schnittspannungsvektor t ist

${\begin{aligned}t=\sigma \cdot n\end{aligned}},$

wobei n ein Normalen-Einheitsvektor ist, der senkrecht auf der Schnittfläche steht und „nach außen“ zeigt. Die Komponenten des Spannungsvektors t bezogen auf das kartesische $(x,y)$-Koordinatensystem werden aus den Komponenten des Spannungstensors und denen des Normalen-Einheitsvektors mittels Matrixmultiplikation bzw. nach der Summenkonvention berechnet als:

${\begin{aligned}{\begin{bmatrix}t_{x}\\t_{y}\\\end{bmatrix}}&={\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}n_{x}\\n_{y}\\\end{bmatrix}}\qquad \Leftrightarrow \qquad {\begin{cases}{\begin{matrix}t_{x}=\sigma _{xx}n_{x}+\tau _{xy}n_{y}\\t_{y}=\tau _{xy}n_{x}+\sigma _{yy}n_{y}\end{matrix}}\end{cases}}\\t^{i}&=\sigma ^{ij}n_{j}\end{aligned}}$

Wenn an einem Schnittufer n der Normalen-Einheitsvektor ist, ist am gegenüber liegenden Schnittufer −n der Normalen-Einheitsvektor. Damit ist das Reaktionsprinzip mit der Definition des Spannungstensors von vornherein erfüllt.

Zusammenhang zwischen den Komponenten des Spannungs­tensors und denen der Schnitt­spannungs­vektoren

Die Komponenten von t bezogen auf das $(x,y)$-Koordinatensystem lassen sich für jede beliebige Schnittrichtung berechnen:

${\begin{aligned}{\begin{bmatrix}t_{x}\\t_{y}\\\end{bmatrix}}&={\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }\\s_{\varphi }\\\end{bmatrix}}\end{aligned}}$

mit den Abkürzungen:

${\begin{aligned}c_{\varphi }&=\cos \varphi \\s_{\varphi }&=\sin \varphi \end{aligned}}$

Besonders einfach ist die Berechnung für Schnitte parallel zu den Koordinatenflächen. Bei $\varphi =0^{\circ }$ ist wegen $(c_{0^{\circ }},s_{0^{\circ }})=(1,0)$:

${\begin{aligned}{\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}}&={\begin{bmatrix}\sigma _{xx}\cdot 1+\tau _{xy}\cdot 0\\\tau _{xy}\cdot 1+\sigma _{yy}\cdot 0\end{bmatrix}}\\&={\begin{bmatrix}\sigma _{xx}\\\tau _{xy}\end{bmatrix}}\end{aligned}}$

Bei $\varphi =90^{\circ }$ ist wegen $(c_{90^{\circ }},s_{90^{\circ }})=(0,1)$:

${\begin{aligned}{\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}}&={\begin{bmatrix}\tau _{xy}\\\sigma _{yy}\end{bmatrix}}\end{aligned}}$

Schnittwinkel $\varphi$	$n_{x}$	$n_{y}$	$t_{x}$	$t_{y}$
$0^{\circ }$	$1$	$0$	$\sigma _{xx}$	$\tau _{xy}$
$90^{\circ }$	$0$	$1$	$\tau _{xy}$	$\sigma _{yy}$
$180^{\circ }$	$-1$	$0$	$-\sigma _{xx}$	$-\tau _{xy}$
$270^{\circ }$	$0$	$-1$	$-\tau _{xy}$	$-\sigma _{yy}$

Die Komponenten des Spannungstensors sind also auch die Komponenten der Spannungen auf den Schnittflächen. Und der Mohr’sche Kreis beschreibt, wie diese Spannungen von der Schnittrichtung abhängen.

(x̅, y̅)-Komponenten

$(t_{x},t_{y})$ und $(t_{\bar {x}},t_{\bar {y}})$

Zählrichtung für Schnitt­winkel $\varphi$ sowie $(t_{\bar {x}},t_{\bar {y}})$ für 12 Schnitt­winkel. Beispiel: ${\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\end{bmatrix}}={\begin{bmatrix}-1&4\\4&5\end{bmatrix}}$

Im Abschnitt (x, y)-Komponenten wurden die Komponenten von t bezogen auf das $(x,y)$-Koordinatensystem angegeben. Die Komponenten von t bezogen auf das $({\bar {x}},{\bar {y}})$-Koordinatensystem sind:

${\begin{aligned}{\begin{bmatrix}t_{\bar {x}}\\t_{\bar {y}}\end{bmatrix}}&={\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\end{bmatrix}}{\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}}\qquad \Leftrightarrow \qquad {\begin{cases}{\begin{matrix}t_{\bar {x}}=c_{\varphi }t_{x}+s_{\varphi }t_{y}\\t_{\bar {y}}=-s_{\varphi }t_{x}+c_{\varphi }t_{y}\end{matrix}}\end{cases}}\end{aligned}}$

Durch Einsetzen und mit Hilfe der Umformungen

${\begin{aligned}t_{\bar {x}}(\varphi )&=t_{x}c_{\varphi }+t_{y}s_{\varphi }\\&=(\sigma _{xx}c_{\varphi }+\tau _{xy}s_{\varphi })c_{\varphi }+(\tau _{xy}c_{\varphi }+\sigma _{yy}s_{\varphi })s_{\varphi }\\&=\sigma _{xx}c_{\varphi }^{2}+2\tau _{xy}s_{\varphi }c_{\varphi }+\sigma _{yy}s_{\varphi }^{2}\\&=\sigma _{xx}{\tfrac {1+c_{2\varphi }}{2}}+\tau _{xy}s_{2\varphi }+\sigma _{yy}{\tfrac {1-c_{2\varphi }}{2}}\\&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})+{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})c_{2\varphi }+\tau _{xy}s_{2\varphi }\\t_{\bar {y}}(\varphi )&=-t_{x}s_{\varphi }+t_{y}c_{\varphi }\\&=-(\sigma _{xx}c_{\varphi }+\tau _{xy}s_{\varphi })s_{\varphi }+(\tau _{xy}c_{\varphi }+\sigma _{yy}s_{\varphi })c_{\varphi }\\&=-\sigma _{xx}s_{\varphi }c_{\varphi }+\tau _{xy}(-s_{\varphi }^{2}+c_{\varphi }^{2})+\sigma _{yy}s_{\varphi }c_{\varphi }\\&=-(\sigma _{xx}-\sigma _{yy})s_{\varphi }c_{\varphi }+\tau _{xy}(-s_{\varphi }^{2}+c_{\varphi }^{2})\\&=-(\sigma _{xx}-\sigma _{yy}){\tfrac {1}{2}}s_{2\varphi }+\tau _{xy}c_{2\varphi }\\\end{aligned}}$

erhält man:

${\begin{aligned}t_{\bar {x}}(\varphi )-{\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})&={\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})c_{2\varphi }+\tau _{xy}s_{2\varphi }\\t_{\bar {y}}(\varphi )&=-{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})s_{2\varphi }+\tau _{xy}c_{2\varphi }\end{aligned}}$

Auf diesen beiden Gleichungen basiert die Konstruktion des Mohr’schen Kreises. Für das Beispiel:

${\begin{aligned}{\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}&={\begin{bmatrix}-1&4\\4&5\\\end{bmatrix}}\end{aligned}}$

sind diese Formeln im Bild „Zählrichtung für Schnittwinkel“ für 12 verschiedene Winkel ausgewertet.

Das Bild „Zählrichtung für Schnittwinkel“ zeigt nicht den Mohr’schen Kreis, sondern veranschaulicht die Formeln für $t_{\bar {x}}$ und $t_{\bar {y}}$. Man sieht an jedem Schnitt den dort wirkenden Schnittspannungsvektor und seine $({\bar {x}},{\bar {y}})$-Komponenten. Den Mohr’schen Kreis erhält man, indem man $t_{\bar {y}}$ über $t_{\bar {x}}$ aufträgt – indem man also ein Diagramm zeichnet, worin die Paare $(t_{\bar {x}},t_{\bar {y}})$ als Punkte dargestellt sind. Dies wird im folgenden Abschnitt getan.

Für Schnitte parallel zu den $(x,y)$-Koordinatenflächen ist:

Schnittwinkel $\varphi$	$n_{x}$	$n_{y}$	$t_{\bar {x}}$	$t_{\bar {y}}$
$0^{\circ }$	$1$	$0$	$\sigma _{xx}$	$\tau _{xy}$
$90^{\circ }$	$0$	$1$	$\sigma _{yy}$	$-\tau _{xy}$
$180^{\circ }$	$-1$	$0$	$\sigma _{xx}$	$\tau _{xy}$
$270^{\circ }$	$0$	$-1$	$\sigma _{yy}$	$-\tau _{xy}$

Kreisgleichung und Hauptspannungen

Kreisgleichung

Innen: Zähl­richtung für $2\varphi$ im Uhrzeigersinn sowie Punkte $(t_{\bar {x}},t_{\bar {y}})$ für $2\varphi =60^{\circ },120^{\circ }$ etc. Außen: Zähl­richtung für $\varphi$ entgegen Uhrzeigersinn sowie Schnitte für $\varphi =30^{\circ },60^{\circ }$ etc., vgl. Bild „Zähl­richtung für Schnitt­winkel“.

Aus den Gleichungen für $t_{\bar {x}}$ und $t_{\bar {y}}$ wird die Kreisgleichung des Mohr’schen Kreises abgeleitet. Quadrieren beider Gleichungen liefert zunächst:

${\begin{aligned}\left(t_{\bar {x}}-{\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\right)^{2}&=\left({\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})c_{2\varphi }+\tau _{xy}s_{2\varphi }\right)^{2}\\t_{\bar {y}}^{2}&=\left(-{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})s_{2\varphi }+\tau _{xy}c_{2\varphi }\right)^{2}\end{aligned}}$

Und durch Addieren dieser Gleichungen erhält man die Gleichung eines Kreises mit Radius R und Mittelpunkt bei (a,b), nämlich:

${\begin{aligned}(t_{\bar {x}}-a)^{2}+(t_{\bar {y}}-b)^{2}&=R^{2}\\(t_{\bar {x}}-\underbrace {{\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})} _{a})^{2}+(t_{\bar {y}}-\underbrace {0} _{b})^{2}&=\underbrace {\left({\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})\right)^{2}+\tau _{xy}^{2}} _{R^{2}}\end{aligned}}$

Der Mittelpunkt des Mohr’schen Kreises liegt bei:

${\begin{aligned}\left(t_{\bar {x}},t_{\bar {y}}\right)=\left(a,b\right)&=\left({\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy}),0\right)\end{aligned}}$

Für das Beispiel ergibt sich (vgl. Bild „Zählrichtung innen/außen“):

${\begin{aligned}\left(a,b\right)&=\left({\tfrac {1}{2}}(-1+5),0\right)\\&=\left(2,0\right)\\\end{aligned}}$

Und der Radius beträgt:

${\begin{aligned}R&={\sqrt {\left({\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})\right)^{2}+\tau _{xy}^{2}}}\end{aligned}}$

Für das Beispiel ergibt sich (vgl. Bild „Zählrichtung innen/außen“):

${\begin{aligned}R&={\sqrt {\left({\tfrac {1}{2}}(-1-5)\right)^{2}+4^{2}}}\\&={\sqrt {9+16}}\\&=5\end{aligned}}$

Hauptspannungen und Hauptspannungsrichtungen

Freischnitte entlang der Hauptspannungsrichtungen und $({\bar {x}},{\bar {y}})$-Komponenten von t für ${\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\end{bmatrix}}={\begin{bmatrix}-1&4\\4&5\end{bmatrix}}$

Die Hauptspannungen sind die Eigenwerte (der Komponentenmatrix) des Spannungstensors. Die charakteristische Gleichung zur Berechnung der Eigenwerte ist:

${\begin{aligned}\det \left({\begin{bmatrix}\sigma _{xx}-\lambda &\tau _{xy}\\\tau _{xy}&\sigma _{yy}-\lambda \\\end{bmatrix}}\right)&=0\end{aligned}}$

Einfache Umformungen

Umformungen

${\begin{aligned}(\sigma _{xx}-\lambda )(\sigma _{yy}-\lambda )-\tau _{xy}^{2}&=0\\\lambda ^{2}-\lambda (\sigma _{xx}+\sigma _{yy})+\sigma _{xx}\sigma _{yy}-\tau _{xy}^{2}&=0\\\lambda _{1/2}&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\pm {\sqrt {{\tfrac {1}{4}}(\sigma _{xx}+\sigma _{yy})^{2}-\sigma _{xx}\sigma _{yy}+\tau _{xy}^{2}}}\\\lambda _{1/2}&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\pm {\sqrt {{\tfrac {1}{4}}(\sigma _{xx}^{2}+\sigma _{yy}^{2}+2\sigma _{xx}\sigma _{yy})-\sigma _{xx}\sigma _{yy}+\tau _{xy}^{2}}}\\\lambda _{1/2}&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\pm {\sqrt {{\tfrac {1}{4}}(\sigma _{xx}^{2}+\sigma _{yy}^{2}-2\sigma _{xx}\sigma _{yy})+\tau _{xy}^{2}}}\\\lambda _{1/2}&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\pm {\sqrt {{\tfrac {1}{4}}(\sigma _{xx}-\sigma _{yy})^{2}+\tau _{xy}^{2}}}\\\end{aligned}}$

führen auf:

${\begin{aligned}\lambda _{1/2}&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})\pm R\end{aligned}},$

sodass man die Hauptspannungen als Schnittpunkte des Kreises mit der $t_{\bar {x}}$-Achse abliest. Für das konkrete Beispiel ergeben sich die Hauptspannungen:

${\begin{aligned}\lambda _{1/2}&=2\pm 5\end{aligned}}$

Es gibt verschiedene Methoden, um die Hauptspannungsrichtungen zu bestimmen.

Berechnung aus Kreisgleichung

Im Spezialfall $t_{\bar {y}}=0$ ist t parallel zum Normalen-Einheitsvektor n.

Aus der Kreisgleichung folgt dann:

${\begin{aligned}0&=\left(-{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})s_{2\varphi _{1/2}}+\tau _{xy}c_{2\varphi _{1/2}}\right)^{2}\\\tan(2\varphi _{1/2})&={\tfrac {2\tau _{xy}}{\sigma _{xx}-\sigma _{yy}}}\end{aligned}}$

Und für das Beispiel ergeben sich die positiven Schnittwinkel:

${\begin{aligned}\tan(2\varphi _{1/2})&=-{\tfrac {4}{3}}\\2\varphi _{1/2}&\approx 127^{\circ }\pm k\pi \\\varphi _{1/2}&\approx 63^{\circ }\pm k{\tfrac {\pi }{2}}\end{aligned}}$

Berechnung aus Eigenvektoren

Die Richtungen lassen sich alternativ mit den Eigenvektoren bestimmen. Der zu $\lambda _{1}=7$ gehörende Eigenvektor $v_{1}$ ist Lösung von:

${\begin{aligned}{\begin{bmatrix}\sigma _{xx}-\lambda _{1}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}-\lambda _{1}\\\end{bmatrix}}{\begin{bmatrix}v_{1_{x}}\\v_{1_{y}}\end{bmatrix}}&=0\\{\begin{bmatrix}v_{1_{x}}\\v_{1_{y}}\end{bmatrix}}&=\alpha {\begin{bmatrix}1\\2\end{bmatrix}}\end{aligned}}$

Die Hauptspannungsrichtung für $\lambda _{2}=-3$ ergibt sich entsprechend zu:

${\begin{aligned}{\begin{bmatrix}v_{2_{x}}\\v_{2_{y}}\end{bmatrix}}&=\alpha {\begin{bmatrix}2\\-1\end{bmatrix}}\end{aligned}}$

Nun liegen die (x,y)-Komponenten beider Eigenvektoren fest. Der Winkel zwischen x-Achse und erstem Eigenvektor ist damit:

${\begin{aligned}\tan(\varphi )&={\tfrac {2}{1}}\\\varphi _{1}&\approx 63^{\circ }\pm k\pi =(\dotsc ,63^{\circ },243^{\circ },\dotsc )\end{aligned}}$

Die zweite Eigenrichtung ist um 90 Grad gegenüber der ersten gedreht, sodass:

${\begin{aligned}\varphi _{2}&\approx 153^{\circ }\pm k\pi =(\dotsc ,-27^{\circ },153^{\circ },\dotsc )\end{aligned}}$

Die Einheitsvektoren der Eigenvektoren bilden eine Orthonormalbasis, die den physikalischen Raum aufspannen, diese Eigenvektoren werden mit $e_{I},e_{II},e_{III}$ bezeichnet. Da der Spannungstensor mit den Einheitseigenvektoren multipliziert (${\vec {T}}=\mathbf {\sigma } \cdot {\vec {n}}$) jeweils eine der Hauptspannungen ergeben, werden sie in diesem Zusammenhang auch $n_{I},n_{II},n_{III}$ bezeichnet.

Mohr’sche Spannungskreise in 3D

Mohr’sche Kreise für einen dreidimensionalen Spannungszustand. Die drei Radien berechnen sich wie im Bild ersichtlich jeweils aus der Differenz zweier Hauptspannungen.

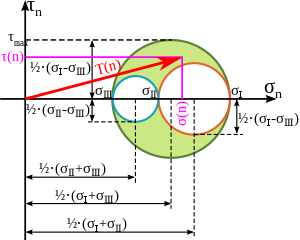
Die dreidimensionale Realität kann man mit 3 Mohr’schen Spannungskreisen darstellen. Es gibt einen äußeren, der die Ebene von σ_III und σ_I aufspannt. Jeder Traktionsvektor muss innerhalb des äußeren Kreises (oder auf dem äußeren Kreis) liegen. Jene Spannungskombinationen aus Normalspannung und Schubspannung, die innerhalb der inneren Kreise liegt, können nicht auftreten, woraus auch folgt, dass es ausschließlich 3 Normalspannungen gibt, bei denen die Schubspannung null ist. Bei einem Spannungszustand, bei dem zwei Hauptspannungen null sind, degeneriert ein Kreis zu einem Punkt und der andere innere Kreis ist identisch mit dem äußeren Kreis. Bei einem hydrostatischen Spannungszustand degenerieren alle drei Kreise zu einem Punkt, da hier keine Schubspannungen vorhanden sind und in jeder Richtung dieselbe Normalspannung vorliegt.

Bestimmung des Normalenvektors bzw. des Traktionsvektors

Wie man die Komponenten von n konstruktiv ermittelt

Konstruktion der Von-Mises-Vergleichs­spannung

Man zeichnet die drei Spannungskreise und jenen Spannungspunkt (den Punkt, auf den der Traktionsvektor T(n) hinweisen soll) ein, der gesucht ist. Dieser Punkt muss sich zwischen den drei Kreisen befinden, liegt er exakt auf einem Kreis kann der Normalenvektor wie bei dem 2D-Spannungskreis ermittelt werden. Ein Spannungspunkt außerhalb des äußeren oder innerhalb eines der kleineren Kreise kann nicht angenommen werden. Durch Einstechen in einem der drei Mittelpunkte der Spannungskreise und Abtragen des Abstandes auf einem der beiden Kreise mit einem anderen Mittelpunkt, kann man wie in 2D den doppelten Winkel zu einer Hauptspannungsrichtung bestimmen. Damit kann man den Normalenvektor bestimmen:

$n=\cos(\alpha _{\mathrm {I} })\cdot n_{I}+\cos(\alpha _{\mathrm {II} })\cdot n_{II}+\cos(\alpha _{\mathrm {III} })\cdot n_{III}=$ ${\begin{pmatrix}\cos(\alpha _{\mathrm {I} }),\cos(\alpha _{\mathrm {II} }),\cos(\alpha _{\mathrm {III} })\end{pmatrix}}_{e_{I},e_{II},e_{III}}^{T}$

Dabei reicht es aus, zwei Winkel zu bestimmen und den dritten über n²=cos²(α_I)+cos²(α_II)+cos²(α_III) zu bestimmen. Ebenso ist eine grafische Bestimmung des Traktionsvektors für einen bestimmten Normalenvektor möglich, hier muss man die zuvor erwähnten Schritte in umgekehrter Reihenfolge durchführen.

Durch die Hauptnormalspannungen σ_I und σ_III wird eine Seite eines gleichseitigen Dreiecks aufgespannt. Der Abstand zwischen dem Punkt des soeben aufgespannten Dreiecks, der nicht auf der Abszisse liegt, und σ_II entspricht der Von-Mises-Vergleichsspannung.

Mohr’scher Kreis: Konstruktion und Auswertung

Konstruktion

Mohr’scher Kreis, Hauptspannungen und Hauptspannungsrichtungen für Beispiel ${\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\end{bmatrix}}={\begin{bmatrix}-1&4\\4&5\end{bmatrix}}$

Die Konstruktion des Mohr’schen Kreises geschieht wie in nebenstehenden Bild dargestellt nach folgendem Schema:

1. Zeichnen eines kart. Koordinatensystems für Punkte $(t_{\bar {x}},t_{\bar {y}})$.
2. Eintragen der zwei Punkte:
   • $P_{0^{\circ }}=\left(t_{\bar {x}}(0^{\circ }),t_{\bar {y}}(0^{\circ })\right)=\left(\sigma _{xx},\tau _{xy}\right)$
   • $P_{90^{\circ }}=\left(t_{\bar {x}}(90^{\circ }),t_{\bar {y}}(90^{\circ })\right)=\left(\sigma _{yy},-\tau _{xy}\right)$.

   Verbinden dieser zwei Punkte durch eine Gerade (strich-punktierte Linie).

3. Zeichnen des Kreises, der die Punkte $P_{0^{\circ }}$ und $P_{90^{\circ }}$ beinhaltet und dessen Mittelpunkt der Schnittpunkt der strichpunktierten Linie mit der $t_{\bar {x}}$-Achse ist.
4. Eintragen/Ablesen der zwei Punkte:
   • $P_{\sigma _{\mathsf {max}}}=(\lambda _{1},0)$
   • $P_{\sigma _{\mathsf {min}}}=(\lambda _{2},0)$

   Verbinden dieser zwei Punkte mit $P_{0^{\circ }}$ (blaue gestrichelte Linien).

5. Eintragen/Ablesen der zwei Punkte:
   • $P_{\tau _{\mathsf {max}}}=(a,R)$
   • $P_{\tau _{\mathsf {min}}}=(a,-R)$

   Verbinden dieser zwei Punkte mit $P_{0^{\circ }}$ (rote gestrichelte Linien).

Auswertung

1. Schnittrichtung / Schnittspannung

Jeder Punkt auf dem Mohr’schen Kreis im Bild im Absatz #Konstruktion entspricht einem Schnittwinkel $\varphi$, siehe Bild „Zähl­richtung für Schnitt­winkel“. $\varphi$ ist einerseits der Winkel zwischen der x-Achse und dem Normalen-Einheitsvektor n – ausgehend von x entgegen dem Uhrzeigersinn positiv gezählt (in Bild „Zähl­richtung für Schnitt­winkel“). Andererseits ist $2\varphi$ im Mohr’schen Kreis, bzw. dem Bild im Absatz #Konstruktion, der Winkel zwischen $P_{0^{\circ }}$ und dem zur jeweiligen Schnittrichtung passenden Punkt $(t_{\bar {x}},t_{\bar {y}})$ – von $P_{0^{\circ }}$ ausgehend im Uhrzeigersinn positiv gezählt.

Für jeden vorgegebenen Schnittwinkel $\varphi$ liest man im Mohr’schen Kreis die $({\bar {x}},{\bar {y}})$-Komponenten des zu dieser Schnittrichtung passenden Schnittspannungsvektors ab. Diese Komponenten sind das Paar $(t_{\bar {x}},t_{\bar {y}})$, das abzulesen ist an der Stelle $2\varphi$.

2. Hauptspannungen

An den Schnittpunkten des Kreises mit der $t_{\bar {x}}$-Achse sind die $({\bar {x}},{\bar {y}})$-Komponenten der Spannungsvektoren $(t_{\bar {x}},t_{\bar {y}})=(\lambda _{1},0)$ bzw. $(t_{\bar {x}},t_{\bar {y}})=(\lambda _{2},0)$. Der Schnittspannungsvektor t ist an diesen Schnittpunkten also parallel zu n, und darum sind $\lambda _{1}$ bzw. $\lambda _{2}$ die Hauptspannungen.

3. Hauptspannungsrichtungen

Die zwei zugehörigen Hauptspannungsrichtungen stehen senkrecht aufeinander. Darum reicht es aus, die zu $\lambda _{1}$ gehörende Richtung abzulesen. Diese ist gegeben durch den Schnittwinkel $\varphi _{1}$, d. h. die Hälfte des Winkels $2\varphi _{1}$ bzw. die blaue gestrichelte Linie zwischen $(\lambda _{2},0)$ und $P_{0^{\circ }}$. Diese Linie/Richtung ist die Hauptspannungsrichtung. Die Richtung, unter der der Freischnitt ausgeführt wird, steht senkrecht dazu. Sie ist durch die blaue gestrichelte Linie zwischen $(\lambda _{1},0)$ und $P_{0^{\circ }}$ gegeben.

4. Extremwerte der Schubspannung

Der Radius des Kreises ist die größte auftretende Schubspannung, d. h.:

${\begin{aligned}\tau _{\textsf {max}}&=t_{{\bar {y}}_{\textsf {max}}}=R\\\tau _{\textsf {min}}&=t_{{\bar {y}}_{\textsf {min}}}=-R\\\end{aligned}}$

Die zugehörigen Schnittwinkel sind um $45^{\circ }$ versetzt zu den Schnittwinkeln, unter denen die Hauptspannungen auftreten (siehe rote gestrichelte Linien im Bild im Absatz #Konstruktion).

Spezialfall: Wenn der Deviator-Anteil des Spannungstensors Null ist – d. h., wenn der Spannungstensor ein Kugeltensor ist – entartet der Kreis zu einem Punkt. Für die Komponenten des Spannungstensors gilt dann in jedem Koordinatensystem:

${\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\end{bmatrix}}=\alpha {\begin{bmatrix}1&0\\0&1\end{bmatrix}}$

Verwandte Themen

Mohr’sche Verzerrungskreise

Analog zu den Mohr’schen Spannungskreisen kann man Mohr’sche Verzerrungskreise zeichnen, die einem aufzeigen, welche Verzerrungszustände angenommen werden. Jedoch gibt es hier keinen Traktionsvektor, der die Spannungskomponenten auf eine beliebige Fläche angibt, wie bei den Spannungskreisen.

Tensorkomponenten aus zwei Schnitten

Spannungstensor-Komponenten $(\sigma _{xx},\sigma _{yy},\tau _{xy})$ bezogen auf das $(x,y)$-Koordinaten­system; Spannungs­tensor-Komponenten $(\sigma _{{\bar {x}}{\bar {x}}},\sigma _{{\bar {y}}{\bar {y}}},\tau _{{\bar {x}}{\bar {y}}})$ bezogen auf das um $\varphi$ gedrehte $({\bar {x}},{\bar {y}})$-Koordinaten­system für Beispiel ${\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\end{bmatrix}}={\begin{bmatrix}-1&4\\4&5\end{bmatrix}}$

Seien die Spannungstensor-Komponenten bezüglich $(x,y)$-Koordinatensystem gegeben. Sei genau ein $({\bar {x}},{\bar {y}})$-Koordinatensystem definiert, das um einen Winkel $\varphi$ gegenüber dem $(x,y)$-Koordinatensystem gedreht ist, siehe nebenstehendes Bild. Seien weiterhin die Spannungstensor-Komponenten bezogen auf dieses eine $({\bar {x}},{\bar {y}})$-Koordinatensystem $(\sigma _{xx},\sigma _{yy},\tau _{xy})$ gesucht.

Dann lassen sich diese Komponenten bestimmen durch einen Schnitt unter $\varphi$ – und einen zweiten Schnitt unter $\varphi +90^{\circ }$, denn:

${\begin{aligned}{\begin{bmatrix}\sigma _{{\bar {x}}{\bar {x}}}\\\tau _{{\bar {x}}{\bar {y}}}\end{bmatrix}}&={\begin{bmatrix}t_{\bar {x}}(\varphi )\\t_{\bar {y}}(\varphi )\\\end{bmatrix}}\\{\begin{bmatrix}\tau _{{\bar {x}}{\bar {y}}}\\\sigma _{{\bar {y}}{\bar {y}}}\end{bmatrix}}&={\begin{bmatrix}-t_{\bar {y}}(\varphi +90^{\circ })\\t_{\bar {x}}(\varphi +90^{\circ })\\\end{bmatrix}}\\&={\begin{bmatrix}t_{\bar {y}}(\varphi )\\t_{\bar {x}}(\varphi +90^{\circ })\\\end{bmatrix}}\end{aligned}}$

Die letzten Formeln ermöglichen es, die Komponenten des Spannungstensors in Bezug auf ein um einen Winkel $\varphi$ gedrehtes Koordinatensystem zu berechnen. Die Funktionen $t_{\bar {x}}$ und $t_{\bar {y}}$, die dazu verwendet werden, sind dieselben wie die zur Konstruktion des Mohr’schen Kreises. Und darum kann man die Komponenten des Spannungstensors in Bezug auf ein gedrehtes Koordinatensystem auch aus dem Mohr’schen Kreis ablesen, siehe hierzu das Bild am Beginn dieses Absatzes.

Tensorkomponenten aus Transformationsbeziehung

Diese $({\bar {x}},{\bar {y}})$-Komponenten des Spannungstensors lassen sich auch direkt aus den $(x,y)$-Komponenten des Spannungstensors berechnen, siehe #Koordinatentransformation. Denn der Koordinatenwechsel von $(x,y)$ auf $({\bar {x}},{\bar {y}})$ erzeugt folgende Transformationsbeziehung (auch Pushforward genannt) für die Komponenten des (2,0)-Spannungstensors:

${\begin{aligned}&{\begin{bmatrix}\sigma _{{\bar {x}}{\bar {x}}}&\tau _{{\bar {x}}{\bar {y}}}\\\tau _{{\bar {x}}{\bar {y}}}&\sigma _{{\bar {y}}{\bar {y}}}\end{bmatrix}}\\=&{\begin{bmatrix}c_{\varphi }&-s_{\varphi }\\s_{\varphi }&c_{\varphi }\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\\\end{bmatrix}}\\=&{\begin{bmatrix}c_{\varphi }\sigma _{xx}-s_{\varphi }\tau _{xy}&c_{\varphi }\tau _{xy}-s_{\varphi }\sigma _{yy}\\s_{\varphi }\sigma _{xx}+c_{\varphi }\tau _{xy}&s_{\varphi }\tau _{xy}+c_{\varphi }\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\\\end{bmatrix}}\\=&{\begin{bmatrix}(c_{\varphi }\sigma _{xx}-s_{\varphi }\tau _{xy})c_{\varphi }-(c_{\varphi }\tau _{xy}-s_{\varphi }\sigma _{yy})s_{\varphi }&(c_{\varphi }\sigma _{xx}-s_{\varphi }\tau _{xy})s_{\varphi }+(c_{\varphi }\tau _{xy}-s_{\varphi }\sigma _{yy})c_{\varphi }\\(s_{\varphi }\sigma _{xx}+c_{\varphi }\tau _{xy})c_{\varphi }-(s_{\varphi }\tau _{xy}+c_{\varphi }\sigma _{yy})s_{\varphi }&(s_{\varphi }\sigma _{xx}+c_{\varphi }\tau _{xy})s_{\varphi }+(s_{\varphi }\tau _{xy}+c_{\varphi }\sigma _{yy})c_{\varphi }\end{bmatrix}}\\=&{\begin{bmatrix}(\sigma _{xx}c_{\varphi }-\tau _{xy}s_{\varphi })c_{\varphi }-(\tau _{xy}c_{\varphi }-\sigma _{yy}s_{\varphi })s_{\varphi }&(\sigma _{xx}c_{\varphi }-\tau _{xy}s_{\varphi })s_{\varphi }+(\tau _{xy}c_{\varphi }-\sigma _{yy}s_{\varphi })c_{\varphi }\\(\sigma _{xx}c_{\varphi }-\tau _{xy}s_{\varphi })s_{\varphi }+(\tau _{xy}c_{\varphi }-\sigma _{yy}s_{\varphi })c_{\varphi }&(\sigma _{xx}c_{\varphi +{\tfrac {\pi }{2}}}+\tau _{xy}s_{\varphi +{\tfrac {\pi }{2}}})c_{\varphi +{\tfrac {\pi }{2}}}+(\tau _{xy}c_{\varphi +{\tfrac {\pi }{2}}}+\sigma _{yy}s_{\varphi +{\tfrac {\pi }{2}}})s_{\varphi +{\tfrac {\pi }{2}}}\end{bmatrix}}\end{aligned}}$

Vergleich mit den Gleichungen für $t_{\bar {x}}$ und $t_{\bar {y}}$ aus Abschnitt #(x̅, y̅)-Komponenten liefert:

${\begin{aligned}{\begin{bmatrix}\sigma _{{\bar {x}}{\bar {x}}}&\tau _{{\bar {x}}{\bar {y}}}\\\tau _{{\bar {x}}{\bar {y}}}&\sigma _{{\bar {y}}{\bar {y}}}\end{bmatrix}}&={\begin{bmatrix}t_{\bar {x}}(\varphi )&t_{\bar {y}}(\varphi )\\t_{\bar {y}}(\varphi )&t_{\bar {x}}\left(\varphi +{\tfrac {\pi }{2}}\right)\end{bmatrix}}\end{aligned}}$

Dieses Ergebnis ist äquivalent zum Ergebnis aus dem letzten Abschnitt, siehe hierzu auch das Bild im Absatz #Tensorkomponenten aus zwei Schnitten.

Häufig wird dieses Ergebnis auch geschrieben als:

${\begin{aligned}\sigma _{{\bar {x}}{\bar {x}}}(\varphi )&={\tfrac {1}{2}}(\sigma _{xx}+\sigma _{yy})+{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})c_{2\varphi }+\tau _{xy}s_{2\varphi }\\\tau _{{\bar {x}}{\bar {y}}}(\varphi )&=-{\tfrac {1}{2}}(\sigma _{xx}-\sigma _{yy})s_{2\varphi }+\tau _{xy}c_{2\varphi }\end{aligned}}$

Umrechnung Flächenträgheitsmomente

Mohr’scher Trägheits­kreis, Haupt­trägheit­smomente $I_{1},I_{2}$ für Beispiel ${\begin{bmatrix}I_{y}&I_{yz}\\I_{yz}&I_{z}\end{bmatrix}}={\begin{bmatrix}3&4\\4&9\end{bmatrix}}$

Die Transformationsregel für Flächenträgheitsmomente kann genau wie die Transformationsregel für die Komponenten des Spannungstensors bestimmt werden. Der Spannungstensor ist eine lineare Abbildung zwischen Vektoren gemäß:

${\begin{aligned}{\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}}&={\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}n_{x}\\n_{y}\end{bmatrix}}\\{\begin{bmatrix}t_{\bar {x}}\\t_{\bar {y}}\end{bmatrix}}&={\begin{bmatrix}\sigma _{{\bar {x}}{\bar {x}}}&\tau _{{\bar {x}}{\bar {y}}}\\\tau _{{\bar {x}}{\bar {y}}}&\sigma _{{\bar {y}}{\bar {y}}}\end{bmatrix}}{\begin{bmatrix}n_{\bar {x}}\\n_{\bar {y}}\end{bmatrix}}\end{aligned}}$

Damit diese Abbildungen unabhängig von der Wahl des Koordinatensystems gelten, müssen die Komponenten des Spannungstensors folgende Transformationsregeln erfüllen:

${\begin{aligned}{\begin{bmatrix}\sigma _{{\bar {x}}{\bar {x}}}&\tau _{{\bar {x}}{\bar {y}}}\\\tau _{{\bar {x}}{\bar {y}}}&\sigma _{{\bar {y}}{\bar {y}}}\end{bmatrix}}&={\begin{bmatrix}c_{\varphi }&-s_{\varphi }\\s_{\varphi }&c_{\varphi }\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}&\tau _{xy}\\\tau _{xy}&\sigma _{yy}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\\\end{bmatrix}}\end{aligned}}$

siehe Euklidische Transformation. Analog gilt bei einem Profilstab zwischen Biegemomenten $M_{y},M_{z}$ und Verkrümmungen $\psi _{y},\psi _{z}$ (bezogen auf die Neutralachse) mit den Flächenträgheitsmomenten definiert als

${\begin{aligned}I_{y}&=\int z^{2}dA\\I_{z}&=\int y^{2}dA\\I_{yz}&=-\int yzdA\\\end{aligned}}$

der lineare Zusammenhang:

${\begin{aligned}{\begin{bmatrix}M_{y}\\M_{z}\end{bmatrix}}&={\begin{bmatrix}EI_{y}&EI_{yz}\\EI_{yz}&EI_{z}\\\end{bmatrix}}{\begin{bmatrix}\psi _{y}\\\psi _{z}\end{bmatrix}}\\{\begin{bmatrix}M_{\bar {y}}\\M_{\bar {z}}\end{bmatrix}}&={\begin{bmatrix}EI_{\bar {y}}&EI_{{\bar {y}}z}\\EI_{{\bar {y}}{\bar {z}}}&EI_{\bar {z}}\\\end{bmatrix}}{\begin{bmatrix}\psi _{\bar {y}}\\\psi _{\bar {z}}\end{bmatrix}}\end{aligned}}$

Die Momente und die Verkrümmungen transformieren sich wie Pseudovektoren – also bei Drehung des Koordinatensystems wie Vektoren. Und darum ist die Transformationsregel für die Flächenträgheitsmomente:

${\begin{aligned}{\begin{bmatrix}EI_{\bar {y}}&EI_{{\bar {y}}{\bar {z}}}\\EI_{{\bar {y}}{\bar {z}}}&EI_{\bar {z}}\\\end{bmatrix}}&={\begin{bmatrix}c_{\varphi }&-s_{\varphi }\\s_{\varphi }&c_{\varphi }\\\end{bmatrix}}{\begin{bmatrix}EI_{y}&EI_{yz}\\EI_{yz}&EI_{z}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\\\end{bmatrix}}\\\Leftrightarrow {\begin{bmatrix}I_{\bar {y}}&I_{{\bar {y}}{\bar {z}}}\\I_{{\bar {y}}{\bar {z}}}&I_{\bar {z}}\\\end{bmatrix}}&={\begin{bmatrix}c_{\varphi }&-s_{\varphi }\\s_{\varphi }&c_{\varphi }\\\end{bmatrix}}{\begin{bmatrix}I_{y}&I_{yz}\\I_{yz}&I_{z}\\\end{bmatrix}}{\begin{bmatrix}c_{\varphi }&s_{\varphi }\\-s_{\varphi }&c_{\varphi }\\\end{bmatrix}}\end{aligned}}$

Der Mohr’sche Kreis kann also zur Umrechnung der Flächenträgheitsmomente bei Koordinatenwechsel ebenso verwendet werden wie zur Umrechnung der Komponenten des Spannungstensors.

Programm zum Ausprobieren

Plot einiger Paare $(t_{\bar {x}},t_{\bar {y}})$, erzeugt mit nebenstehendem Programm

mit Matplotlib und NumPy

import matplotlib.pyplot as plt
from numpy import pi, sin, cos, array, transpose, dot
from numpy import radians, degrees, set_printoptions

#There is the (x,y)-system and the (X,Y)-system.

#         [s_xx  t_xy ]     [-1  4 ]
#  S_xy = [           ]  =  [      ]
#         [t_xy  s_yy ]     [ 4  5 ]

# ---
# --- User input:
# ---

# 1: Stress tensor components:
(s_xx, s_yy, t_xy) = (-1, 5, 4)

# 2: List of angles phi in degrees:
phi_deg = array( [0., 30., 60., 90., 120., 150.] )

# ---
# --- Program output:
# ---

# phi [ t_X, t_Y ]

# 0.0  [-1.   4.  ]
# 30.0 [ 3.96 4.6 ]
# 60.0 [ 6.96 0.6 ]
# ...

# phi [ s_XX, t_XY ]
#     [ t_XY, s_YY ]

# 0.0   [-1.   4.  ]
#       [ 4.   5.  ]
# 30.0  [ 3.96 4.6 ]
#       [ 4.6  0.04]
# 60.0  [ 6.96 0.6 ]
#       [ 0.6 -2.96]
# ...

# ---
# --- Program:
# ---

# Matrix of components::
S_xy = array([ [s_xx, t_xy],
               [t_xy, s_yy] ])

# Yes
half = 0.5
two  = 2.0

# Some functions for later use:
def c2(phi):
    """ computes cos(2 phi) """
    return cos(two*phi)

def s2(phi):
    """ computes sin(2 phi) """
    return sin(two*phi)

def get_t_X(phi):
    """
    computes t_X(phi) as in section
    "(X,Y)-Komponenten"
    """
    t_X = half*(s_xx + s_yy) + half*(s_xx - s_yy) * c2(phi) + t_xy*s2(phi)
    return t_X

def get_t_Y(phi):
    """
    computes t_Y(phi) as in section
    "(X,Y)-Komponenten"
    """
    t_Y = -half*(s_xx - s_yy) * s2(phi) + t_xy * c2(phi)
    return t_Y

def get_t_XY(phi):
    """
    computes pair (t_X, t_Y)
    """
    t_X = get_t_X(phi)
    t_Y = get_t_Y(phi)
    return array([t_X, t_Y])

def get_R(phi):
    """
    computes rotation matrix as in section
    "Tensorkomponenten aus Transformationsbeziehung"
    """
    Rt = array([ [ cos(phi), sin(phi)],
                 [-sin(phi), cos(phi)] ] )
    return Rt

def get_S_XY(phi):
    """
    computes S_XY = R * S_xy * R^T as in section
    "Tensorkomponenten aus Transformationsbeziehung"
    """
    R = get_R(phi)
    R_T = R.transpose()
    S_XY = dot( dot(R, S_xy), R_T )
    return S_XY

# Compute and plot some pairs (t_X, t_Y):

# phi in radians:
phis = array( [ radians(a) for a in phi_deg ] )

# for prettier printing:
set_printoptions(precision=2)

print ()
print ("phi   [ t_X, t_Y ]")
print ()
for phi in phis:
    tX_tY = get_t_XY(phi)
    print (degrees(phi),"  ", tX_tY)

print ()
print ("phi   [ s_XX, t_XY ]")
print ("      [ t_XY, s_YY ]")
print ()
for phi in phis:
    S_XY = get_S_XY(phi)
    print (degrees(phi), "  ", S_XY[0])
    print ("       ",         S_XY[1])

# Now plot these pairs (t_X, t_Y):

# phi --> t_X(phi):
t_X = list(map(get_t_X, phis))
# phi --> t_Y(phi):
t_Y = list(map(get_t_Y, phis))

# color = phi in degrees:
color = degrees(phis)

# make the circle be a circle:
plt.axis("equal")

# plot some colored points:
plt.scatter(t_X, t_Y, s=100, c=color)

# add colorbar:
cbar = plt.colorbar()

# plt.clim(0,180.)
# add ticks to colorbar:
cbar.set_ticks(degrees(phis))

# show plot:
plt.show()

Weblinks

Commons: Mohr's circle – Sammlung von Bildern, Videos und Audiodateien

• Visualisierung symmetrischer Tensoren mit Superquadriken

Literatur

• Otto Mohr: Abhandlungen aus dem Gebiete der technischen Mechanik. Ernst & Sohn, Berlin 1906 (archive.org). 
• Gross, Hauger, Schröder, Wall: Technische Mechanik 2. 12. Auflage. Springer Vieweg, 2012, ISBN 978-3-642-40965-3. 
• F. Jung: Der Culmannsche und der Mohr’sche Kreis. In: Österreichisches Ingenieur-Archiv. Band 1, Nr. 4–5, 1946, ISSN 0369-7819, S. 408–410. 
• Istvan Szabo: Einführung in die Technische Mechanik. Springer, 1984, ISBN 3-540-13293-7. 
• Jerrold E. Marsden, Thomas J. R. Hughes: Mathematical Foundations of Elasticity. 1994, ISBN 0-486-67865-2. 
• Walter Noll, Clifford Truesdell: The Non-Linear Field Theories of Mechanics. Springer-Verlag, New York 1965, ISBN 3-540-02779-3. 
• Walter Noll: Foundations of Mechanics and Thermodynamics, Selected Papers. Springer-Verlag, New York 1974, ISBN 0-387-06646-2. 
• Stephen P. Timoshenko, James Norman Goodier: Theory of Elasticity. 3. Auflage. McGraw-Hill International Editions, 1970, ISBN 0-07-085805-5. 
• Stephen P. Timoshenko: History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures (= Dover Books on Physics). Dover Publications, 1983, ISBN 0-486-61187-6. 
• Johannes Wiedemann: Leichtbau. Band 1: Elemente. Springer, 1986, ISBN 3-540-16404-9. 
• Christian Spura: Technische Mechanik. 2. Elastostatik. Springer, 2019, ISBN 978-3-658-19978-4. 

Kategorie:Festigkeitslehre