Ellipsoid

Rotationsellipsoid (unten links), ,
triaxiales Ellipsoid (unten rechts),
Ein Ellipsoid ist die 3-dimensionale Entsprechung einer Ellipse. So wie sich eine Ellipse als affines Bild des Einheitskreises auffassen lässt, gilt:
- Ein Ellipsoid (als Fläche) ist ein affines Bild der Einheitskugel
Die einfachsten affinen Abbildungen sind die Skalierungen der kartesischen Koordinaten. Sie liefern Ellipsoide mit Gleichungen
Solch ein Ellipsoid ist punktsymmetrisch zum Punkt , dem Mittelpunkt des Ellipsoids. Die Zahlen sind analog zu einer Ellipse die Halbachsen des Ellipsoids und die Punkte seine 6 Scheitelpunkte.
- Falls ist, ist das Ellipsoid eine Kugel.
- Falls genau zwei Halbachsen übereinstimmen, ist das Ellipsoid ein prolates oder oblates Rotationsellipsoid.
- Falls die 3 Halbachsen alle verschieden sind, heißt das Ellipsoid triaxial oder dreiachsig.
Alle Ellipsoide sind symmetrisch zu jeder der drei Koordinatenebenen. Beim Rotationsellipsoid kommt noch die Rotationssymmetrie bezüglich der Rotationsachse hinzu. Eine Kugel ist zu jeder Ebene durch den Mittelpunkt symmetrisch.

Angenäherte Beispiele für Rotationsellipsoide sind der Rugbyball und abgeplattete rotierende Himmelskörper, etwa die Erde oder andere Planeten (Jupiter), Sonnen oder Galaxien. Elliptische Galaxien und Zwergplaneten (z. B. (136108) Haumea) können auch triaxial sein.
In der Linearen Optimierung werden Ellipsoide in der Ellipsoid-Methode verwendet.
Parameterdarstellung[Bearbeiten | Quelltext bearbeiten]

Die Punkte auf der Einheitskugel können wie folgt parametrisiert werden (siehe Kugelkoordinaten):
Für den Winkel (von der z-Achse aus gemessen) gilt . Für den Winkel (von der x-Achse aus gemessen) gilt .
Skaliert man die einzelnen Koordinaten mit den Faktoren , so ergibt sich eine Parameterdarstellung des Ellipsoids :
mit und
Volumen[Bearbeiten | Quelltext bearbeiten]
Das Volumen des Ellipsoids ist
Eine Kugel mit Radius hat das Volumen
- Herleitung
Der Schnitt des Ellipsoids mit einer Ebene in der Höhe ist die Ellipse mit den Halbachsen
- .
Der Flächeninhalt dieser Ellipse ist . Das Volumen ergibt sich dann aus
Oberfläche[Bearbeiten | Quelltext bearbeiten]
Oberfläche eines Rotationsellipsoids[Bearbeiten | Quelltext bearbeiten]
Die Oberfläche eines abgeplatteten Rotationsellipsoids mit ist
die des verlängerten Ellipsoids ()
Eine Kugel mit Radius hat die Oberfläche .
Oberfläche eines triaxialen Ellipsoids[Bearbeiten | Quelltext bearbeiten]
Die Oberfläche eines triaxialen Ellipsoids lässt sich nicht mit Hilfe von Funktionen ausdrücken, die man als elementar ansieht, wie z. B. oder oben beim Rotationsellipsoid. Die Flächenberechnung gelang Adrien-Marie Legendre mit Hilfe der elliptischen Integrale. Sei . Schreibt man
- und
so lauten die Integrale
- und
Die Oberfläche hat mit und nach Legendre[1] den Wert
Werden die Ausdrücke für und sowie die Substitutionen
- und
in die Gleichung für eingesetzt, so ergibt sich die Schreibweise
Von Knud Thomsen stammt die integralfreie Näherungsformel[2]
Die maximale Abweichung vom exakten Resultat beträgt weniger als 1,2 %.
Im Grenzfall eines vollständig plattgedrückten Ellipsoids streben alle drei angegebenen Formeln für gegen den doppelten Wert des Flächeninhalts einer Ellipse mit den Halbachsen und .
Anwendungsbeispiel zu den Formeln[Bearbeiten | Quelltext bearbeiten]
Der Planet Jupiter ist wegen den durch die schnelle Rotation wirkenden Zentrifugalkräften an den Polen deutlich flacher als am Äquator und hat annähernd die Form eines Rotationsellipsoids.
Der Jupiter hat den Äquatordurchmesser 142984 km und den Poldurchmesser 133708 km. Also gilt für die Halbachsen und . Die Masse des Jupiter beträgt etwa 1,899 · 1027 kg. Daraus ergibt sich mithilfe der oben genannten Formeln für das Volumen, die mittlere Dichte und die Oberfläche:
- Volumen:
- Das ist etwa 1321-mal so viel wie das Volumen der Erde.
- Mittlere Dichte:
- Der Jupiter hat also insgesamt eine etwas höhere Dichte als Wasser unter Standardbedingungen.
- Oberfläche:
- Das ist etwa 121-mal so viel wie die Oberfläche der Erde.
Ebene Schnitte[Bearbeiten | Quelltext bearbeiten]
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
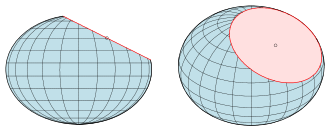
Der Schnitt eines Ellipsoids mit einer Ebene ist
- eine Ellipse, falls er wenigstens zwei Punkte enthält,
- ein Punkt, falls die Ebene eine Tangentialebene ist,
- andernfalls leer.
Der erste Fall folgt aus der Tatsache, dass eine Ebene eine Kugel in einem Kreis schneidet und ein Kreis bei einer affinen Abbildung in eine Ellipse übergeht. Dass einige der Schnittellipsen Kreise sind, ist bei einem Rotationsellipsoid offensichtlich: Alle ebenen Schnitte, die wenigstens 2 Punkte enthalten und deren Ebenen senkrecht zur Rotationsachse sind, sind Kreise. Dass aber auch jedes 3-achsige Ellipsoid viele Kreise enthält, ist nicht offensichtlich und wird in Kreisschnittebene erklärt.
Der wahre Umriss eines beliebigen Ellipsoids ist sowohl bei Parallelprojektion als auch bei Zentralprojektion ein ebener Schnitt, also eine Ellipse (siehe Bilder).
Bestimmung einer Schnittellipse[Bearbeiten | Quelltext bearbeiten]

Gegeben: Ellipsoid und eine Ebene mit der Gleichung die das Ellipsoid in einer Ellipse schneidet.
Gesucht: Drei Vektoren (Mittelpunkt) und (konjugierte Vektoren) so, dass die Schnittellipse durch die Parameterdarstellung
beschrieben werden kann (siehe Ellipse).

Lösung: Die Skalierung führt das Ellipsoid in die Einheitskugel und die gegebene Ebene in die Ebene mit der Gleichung über. Die Hesse-Normalform der neuen Ebene sei mit dem Normaleneinheitsvektor Dann ist
der Mittelpunkt des Schnittkreises und dessen Radius
Falls ist, sei (Die Ebene ist horizontal!)
Falls ist, sei
Die Vektoren sind in jedem Fall zwei in der Schnittebene liegende orthogonale Vektoren der Länge (Kreisradius), d. h., der Schnittkreis wird durch die Parameterdarstellung beschrieben.
Macht man nun die obige Skalierung (affine Abbildung) rückgängig, so wird die Einheitskugel wieder zum gegebenen Ellipsoid und man erhält aus den Vektoren die gesuchten Vektoren , mit denen man die Schnittellipse beschreiben kann. Wie man daraus die Scheitelpunkte der Ellipse und damit ihre Halbachsen bestimmt, wird unter Ellipse erklärt.
Beispiel: Die Bilder gehören zu dem Beispiel mit und der Schnittebene Das Bild des Ellipsoidschnittes ist eine senkrechte Parallelprojektion auf eine Ebene parallel zur Schnittebene, d. h., die Ellipse erscheint bis auf eine uniforme Skalierung in wahrer Gestalt. Man beachte, dass hier im Gegensatz zu nicht auf der Schnittebene senkrecht steht. Die Vektoren sind hier im Gegensatz zu nicht orthogonal.
Fadenkonstruktion[Bearbeiten | Quelltext bearbeiten]

Länge des Fades (rot)


Die Fadenkonstruktion eines Ellipsoids ist eine Übertragung der Idee der Gärtnerkonstruktion einer Ellipse (siehe Abbildung). Eine Fadenkonstruktion eines Rotationsellipsoids ergibt sich durch Konstruktion der Meridian-Ellipsen mit Hilfe eines Fadens.
Punkte eines 3-achsigen Ellipsoids mit Hilfe eines gespannten Fadens zu konstruieren ist etwas komplizierter. Wolfgang Boehm schreibt in dem Artikel Die Fadenkonstruktion der Flächen zweiter Ordnung[3] die Grundidee der Fadenkonstruktion eines Ellipsoids dem schottischen Physiker James Clerk Maxwell (1868) zu. Otto Staude hat in Arbeiten 1882, 1886, 1898[4][5][6] die Fadenkonstruktion dann auf Quadriken verallgemeinert. Die Fadenkonstruktion für Ellipsoide und Hyperboloide wird auch in dem Buch Anschauliche Geometrie[7] von David Hilbert und Stefan Cohn-Vossen beschrieben. Auch Sebastian Finsterwalder beschäftigte sich 1886 mit diesem Thema.[8]
- Konstruktionsschritte
- (1) Man wähle eine Ellipse und eine Hyperbel, die ein Paar von Fokalkegelschnitten bilden:
- Ellipse: und
- Hyperbel:
- mit den Scheitelpunkten und Brennpunkten der Ellipse
- und einen Faden (in der Abbildung Bild rot) der Länge .
- (2) Man befestige das eine Ende des Fadens im Scheitelpunkt und das andere Ende im Brennpunkt . Der Faden wird in einem Punkt so gespannt gehalten, dass der Faden von hinten auf der Hyperbel und von vorn auf der Ellipse gleiten kann (siehe Abbildung). Der Faden geht über denjenigen Hyperbelpunkt, mit dem die Entfernung von nach über einen Hyperbelpunkt minimal wird. Analoges gilt für den Fadenteil von nach über einen Ellipsenpunkt.
- (3) Wählt man den Punkt so, dass er positive y- und z-Koordinaten hat, so ist ein Punkt des Ellipsoids mit der Gleichung
- und
- (4) die restlichen Punkte des Ellipsoids erhält man durch geeignetes Umspannen des Fadens an den Fokalkegelschnitten.
Die Gleichungen für die Halbachsen des erzeugten Ellipsoids ergeben sich, wenn man den Punkt in die beiden Scheitelpunkte fallen lässt:
Aus der unteren Zeichnung erkennt man, dass auch die Brennpunkte der Äquatorellipse sind. D. h.: Die Äquatorellipse ist konfokal zur gegebenen Fokalellipse. Also ist , woraus sich ergibt. Ferner erkennt man, dass ist.
Aus der oberen Zeichnung ergibt sich: sind die Brennpunkte der Ellipse in der x-z-Ebene und es gilt .
Umkehrung:
Möchte man ein durch seine Gleichung gegebenes 3-achsiges Ellipsoid mit den Halbachsen konstruieren, so lassen sich aus den Gleichungen im Schritt (3) die für die Fadenkonstruktion nötigen Parameter berechnen. Für die folgenden Überlegungen wichtig sind die Gleichungen
- (5)
Konfokale Ellipsoide:
Ist ein zu konfokales Ellipsoid mit den Quadraten der Halbachsen
- (6)
so erkennt man aus den vorigen Gleichungen, dass die zu gehörigen Fokalkegelschnitte für die Fadenerzeugung dieselben Halbachsen wie die von besitzen. Deshalb fasst man – analog der Rolle der Brennpunkte bei der Fadenerzeugung einer Ellipse – die Fokalkegelschnitte eines 3-achsigen Ellipsoids als deren unendlich viele Brennpunkte auf und nennt sie Fokalkurven des Ellipsoids.[9]
Auch die Umkehrung ist richtig: Wählt man einen zweiten Faden der Länge und setzt , so gilt D. h.: Die beiden Ellipsoide sind konfokal.
Grenzfall Rotationsellipsoid:
Im Fall ist , d. h., die Fokalellipse artet in eine Strecke und die Hyperbel in zwei Strahlen auf der x-Achse aus. Das Ellipsoid ist dann ein Rotationsellipsoid mit der x-Achse als Rotationsachse. Es ist .

Eigenschaften der Fokalhyperbel:
Betrachtet man ein Ellipsoid von einem außerhalb gelegenen Punkt auf der zugehörigen Fokalhyperbel aus, so erscheint der Umriss des Ellipsoids als Kreis. Oder, anders ausgedrückt: Die Tangenten des Ellipsoids durch bilden einen senkrechten Kreiskegel, dessen Rotationsachse Tangente in an die Hyperbel ist.[10][11] Lässt man den Augpunkt ins Unendliche laufen, entsteht die Ansicht einer senkrechten Parallelprojektion mit einer Asymptote der Fokalhyperbel als Projektionsrichtung. Die wahre Umrisskurve auf dem Ellipsoid ist im Allgemeinen kein Kreis.
In der Abbildung ist unten links eine Parallelprojektion eines 3-achsigen Ellipsoids (Halbachsen: 60,40,30) in Richtung einer Asymptote und unten rechts eine Zentralprojektion mit Zentrum auf der Fokalhyperbel und Hauptpunkt auf der Tangente an die Hyperbel in dargestellt. In beiden Projektionen sind die scheinbaren Umrisse Kreise. Links ist das Bild des Koordinatenursprungs der Mittelpunkt des Umrisskreises, rechts ist der Hauptpunkt der Mittelpunkt.
Die Fokalhyperbel eines Ellipsoids schneidet das Ellipsoid in seinen vier Nabelpunkten.[12]
Eigenschaft der Fokalellipse:
Die Fokalellipse mit ihrem Inneren kann als Grenzfläche der durch bestimmten Schar von konfokalen Ellipsoide für als unendlich dünnes Ellipsoid angesehen werden. Es ist dann
Ellipsoid in beliebiger Lage[Bearbeiten | Quelltext bearbeiten]
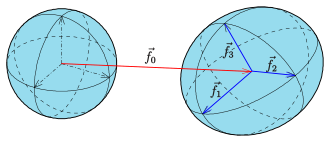
Parameterdarstellung[Bearbeiten | Quelltext bearbeiten]
Eine affine Abbildung lässt sich durch eine Parallelverschiebung um und eine reguläre 3×3-Matrix beschreiben:
- ,
wobei die Spaltenvektoren der Matrix sind.
Die Parameterdarstellung eines beliebigen Ellipsoids ergibt sich aus der obigen Parameterdarstellung der Einheitskugel und der Beschreibung einer affinen Abbildung:
Umgekehrt gilt: Wählt man einen Vektor beliebig und die Vektoren beliebig, aber linear unabhängig, so beschreibt die obige Parameterdarstellung in jedem Fall ein Ellipsoid. Bilden die Vektoren ein Orthogonalsystem, so sind die Punkte die Scheitelpunkte des Ellipsoids und die zugehörigen Halbachsen.
Ein Normalenvektor im Punkt ist
Zu einer Parameterdarstellung eines beliebigen Ellipsoids lässt sich auch eine implizite Beschreibung angeben. Für ein Ellipsoid mit Mittelpunkt im Koordinatenursprung, d. h. , ist
eine implizite Darstellung.[13]
Bemerkung: Das durch obige Parameterdarstellung beschriebene Ellipsoid ist in dem eventuell schiefen Koordinatensystem (Koordinatenursprung), (Basisvektoren) die Einheitskugel.
Ellipsoid als Quadrik[Bearbeiten | Quelltext bearbeiten]
Ein beliebiges Ellipsoid mit Mittelpunkt lässt sich als Lösungsmenge einer Gleichung
schreiben, wobei eine positiv definite Matrix ist.
Die Eigenvektoren der Matrix bestimmen die Hauptachsenrichtungen des Ellipsoids und die Eigenwerte von sind die Kehrwerte der Quadrate der Halbachsen: , und .[14]
Ellipsoid in der projektiven Geometrie[Bearbeiten | Quelltext bearbeiten]
Schließt man den 3-dimensionalen affinen Raum und die einzelnen Quadriken projektiv durch eine Fernebene bzw. Fernpunkte ab, so sind die folgenden Quadriken projektiv äquivalent, d. h., es gibt jeweils eine projektive Kollineation, die die eine Quadrik in die andere überführt:
- Ellipsoid, elliptisches Paraboloid und 2-schaliges Hyperboloid.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Rotationsellipsoid
- Referenzellipsoid
- Trägheitsellipsoid
- Indexellipsoid
- Homöoid
- Fokaloid
- Konfokale Quadriken
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Online-Berechnung von Volumen und Oberfläche eines Ellipsoids (englisch)
- Herleitung der Formel für die Oberfläche eines Ellipsoids. Juli 2003, archiviert vom am 3. Februar 2015; abgerufen am 3. Februar 2015 (englisch).
- Mathematische Basteleien: Ellipsoid
- Eric W. Weisstein: Ellipsoid. In: MathWorld (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Adrien-Marie Legendre: Traite des fonctions elliptiques et des intégrales Euleriennes, Bd. 1. Hugard-Courier, Paris 1825, S. 357.
- ↑ Suzanne M. Kresta, Arthur W. Etchells III, David S. Dickey, Victor A. Atiemo-Obeng (Hrsg.): Advances in Industrial Mixing: A Companion to the Handbook of Industrial Mixing. John Wiley & Sons, 11. März 2016, ISBN 978-0-470-52382-7, Seite 524 unten in der Google-Buchsuche.
- ↑ W. Böhm: Die FadenKonstruktion der Flächen zweiter Ordnung, Mathemat. Nachrichten 13, 1955, S. 151.
- ↑ O. Staude: Ueber Fadenconstructionen des Ellipsoides. Math. Ann. 20, 147–184 (1882).
- ↑ O. Staude: Ueber neue Focaleigenschaften der Flächen 2. Grades. Math. Ann. 27, 253–271 (1886).
- ↑ O. Staude: Die algebraischen Grundlagen der Focaleigenschaften der Flächen 2. Ordnung. Math. Ann. 50, 398–428 (1898).
- ↑ D. Hilbert & S. Cohn-Vossen: Anschauliche Geometrie. Springer-Verlag, 2013, ISBN 3662366851, S. 18.
- ↑ S. Finsterwalder: Über die Fadenconstruction des Ellipsoides. Mathematische Annalen Bd. 26, 1886, S. 546–556.
- ↑ O. Hesse: Analytische Geometrie des Raumes. Teubner, Leipzig 1861, S. 287.
- ↑ D. Hilbert, S. Cohn-Vossen: Anschauliche Geometrie. S. 22.
- ↑ O. Hesse: Analytische Geometrie des Raumes. S. 301.
- ↑ W. Blaschke: Analytische Geometrie. S. 125.
- ↑ Computerunterstützte Darstellende und Konstruktive Geometrie. Uni Darmstadt (PDF; 3,4 MB), S. 88.
- ↑ Symmetric matrices, quadratic forms, matrix norm, and SVD.


































































































































