Friesgruppe
Fries- oder Bandornamentgruppen sind spezielle Gruppen, die in der Mathematik, genauer der diskreten Geometrie, untersucht werden.
Grundidee[Bearbeiten | Quelltext bearbeiten]
Bandornamente (oder Friese) sind Muster, die gebildet werden, indem man eine bestimmte kleinste Einheit (z. B. ein Muster oder eine Figur) entlang einer festen Richtung (der sogenannten Friesrichtung) immer wieder aneinandersetzt. Eine Bandornamentgruppe wiederum ist anschaulich gesehen die Symmetriegruppe eines bestimmten Bandornamentes, dabei stellt man sich das Bandornament allerdings in beide Richtungen ins Unendliche verlängert vor. Bandornamente können viele verschiedene Formen und Figuren aufweisen, die mathematisch schwer handhabbar sind, so dass Bandornamentgruppen mathematisch gesehen nur schlecht auf diese Art und Weise definiert werden können.
Allerdings haben alle Bandornamentgruppen eines gemeinsam: Aufgrund seiner Konstruktion wird ein Bandornament auf jeden Fall auf sich selbst abgebildet, wenn man es um eine Einheit oder um ein Vielfaches dieser Einheit entlang der Friesrichtung verschiebt. Solche Verschiebungen oder Translationen (Parallelverschiebungen) gehören also zu der Symmetriegruppe eines Bandornamentes. Sie sind aber auch die einzig möglichen Verschiebungen, die ein

Bandornament auf sich abbildet, insbesondere treten keinerlei Verschiebungen in eine andere Richtung als in Friesrichtung (bzw. in die entgegengesetzte Richtung) auf. Die einzigen Verschiebungen, die also innerhalb einer Symmetriegruppe eines Frieses auftauchen können und müssen, sind Verschiebungen um ein Vielfaches eines Vektors, dessen Länge gleich dem Abstand zwischen zwei kleinsten Einheiten ist und der in Friesrichtung zeigt. Bezeichnet man einen solchen Vektor mit , so gilt für jede Verschiebung aus der Symmetriegruppe des Frieses: . Mit anderen Worten: Alle in der Symmetriegruppe des Bandornamentes vorkommenden Verschiebungen gehören zu der von erzeugten Gruppe, insbesondere bilden die Translationen einer Bandornamentgruppe eine zyklische Gruppe. Diese Eigenschaft von Friessymmetriegruppen wird zur mathematischen Definition einer Bandornamentgruppe herangezogen.
Mathematische Definition[Bearbeiten | Quelltext bearbeiten]
- Friesgruppe
- Sei ein zweidimensionaler euklidischer Raum und die Menge seiner Isometrien. Eine Untergruppe heißt Friesgruppe, wenn die Gruppe seiner Translationen zur additiven Gruppe isomorph ist, d. h. wenn eine Translation existiert, so dass für jede beliebige Translation gilt: mit passendem .
Den zu einer erzeugenden Translation gehörigen Translationsvektor nennt man auch Friesvektor, er ist bis auf das Vorzeichen eindeutig bestimmt. Die Gerade heißt Friesrichtung. Da die Menge der Translationen einer aus Isometrien bestehenden Gruppe selbst wieder eine Gruppe ist, nennt man T(G) auch die Translationsgruppe von G. Es sei darauf hingewiesen, dass die n-fache Hintereinanderschaltung der Abbildung bezeichnet und dass gilt:
Hintergrund: Ist eine diskrete Bewegungsgruppe der Ebene, so gibt es nur drei Möglichkeiten:[1] 1) , und ist eine Punktgruppe; 2) , und ist eine Friesgruppe; 3) , und ist eine Ornamentgruppe.
Klassifizierung[Bearbeiten | Quelltext bearbeiten]
Bei genauerer Untersuchung stellt man fest, dass es „so viele“ Friesgruppen gar nicht gibt, d. h. viele Friesgruppen sind sich in einem gewissen Sinn ähnlich. Dabei denkt man an den Ähnlichkeitsbegriff, der im nächsten Abschnitt definiert wird.
Klassifizierung[Bearbeiten | Quelltext bearbeiten]
- Ähnlichkeit
- Zwei Untergruppen und heißen ähnlich, wenn es eine bijektive affine Abbildung gibt mit
Die Ähnlichkeit von Gruppen hat die Eigenschaften einer Äquivalenzrelation, so dass man mit der Definition der Ähnlichkeit die Menge aller Untergruppen von disjunkt zerlegt.
Es zeigt sich, dass es nur sieben Typen von Bandornamentgruppen bzgl. der Ähnlichkeit gibt. Wählt man also eine beliebige Bandornamentgruppe G aus, so gibt es eine Gruppe H von einem der sieben nachfolgend beschriebenen Typen sowie eine bijektive affine Abbildung mit . Alle Typen sind systematisch durchnummeriert und in der nachfolgenden Liste aufgeführt und beschrieben (im Folgenden sei ein Erzeugendenelement der Translationsgruppe von G).
Typen von Bandornamentgruppen:
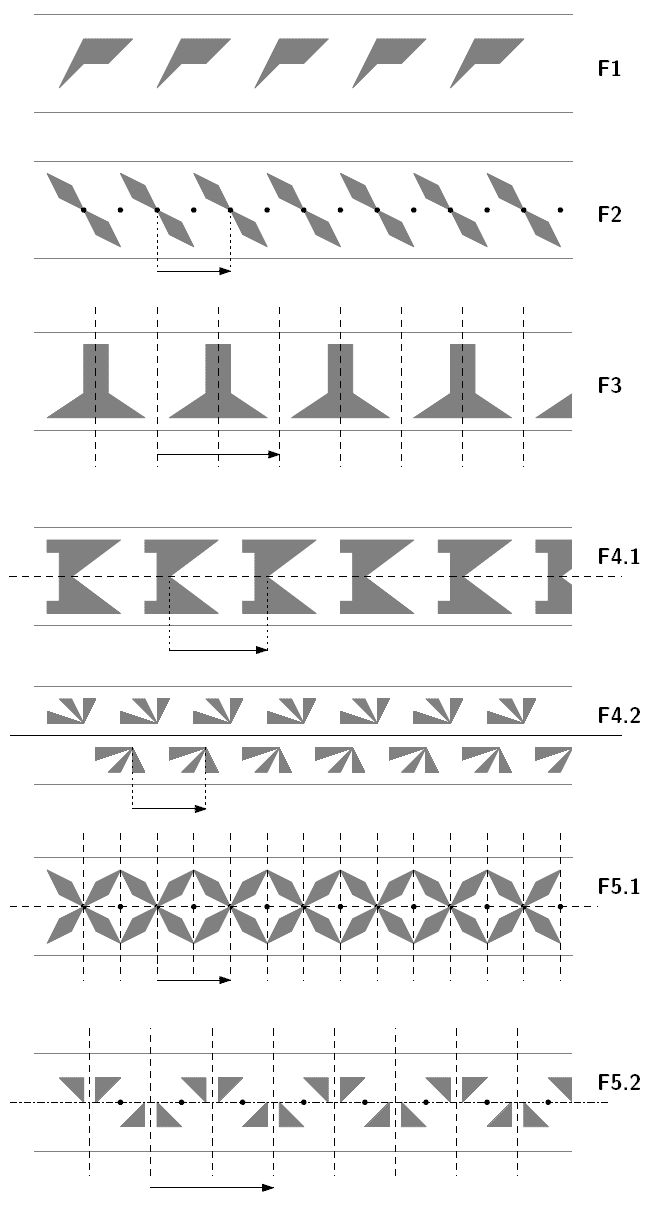
| F1 | Eine Gruppe des Typs F1 enthält nur Translationen der Form . |
| F2 | Gruppen des Typs F2 enthalten nur Translationen von obigem Typ sowie Punktspiegelungen an Zentren der Form mit |
| F3 | Bandornamentgruppen dieses Typs enthalten Translationen sowie Spiegelungen an Achsen senkrecht zu Friesrichtung. Die Achsen verlaufen durch die Punkte |
| F4.1 | Solche Gruppen bestehen aus Translationen und aus (Schub-)spiegelungen an einer Achse parallel zur Friesrichtung. Die Verschiebevektoren dieser Schubspiegelungen sind von der Form |
| F4.2 | Gruppen des Typs 4.2 enthalten Translationen sowie Schubspiegelungen an einer Achse parallel zur Friesrichtung mit Verschiebevektor der Form . |
| F5.1 | Gruppen dieses Typs enthalten die gleichen Abbildungen wie Gruppen des Typs F4.1 und zusätzlich die Abbildungen des Typs F2 und F3. |
| F5.2 | Enthält alle Abbildungen, die unter F2, F3 und F4.2 beschrieben sind. |
Beweis der Klassifizierung (Skizze)[Bearbeiten | Quelltext bearbeiten]
Der Beweis der Klassifizierung wird über die sogenannte Punktgruppe S(G) einer Friesgruppe G geführt. Die Punktgruppe von G besteht aus allen linearen Anteilen der Abbildungen aus G: . Im Beweis überlegt man sich, welche Punktgruppen möglich sind und rekonstruiert daraus mögliche Friesgruppen.
Da die Translationsgruppe zyklisch ist, enthält sie eine Translation mit kürzestmöglichem Translationsvektor. Dies zeigt man leicht, denn alle zu Translationen gehörige Vektoren sind von der Form , wenn ein Vektor gehörig zu einem Erzeugendenelement der Translationsgruppe ist. Offenbar sind die kürzestmöglichen zu einer Translation gehörigen Vektoren. Wir betrachten nun ein beliebiges Element einer Friesgruppe, mit (also mit Verschiebevektor v und linearem Anteil L). Aufgrund der Gruppeneigenschaften von G befindet sich mit und auch in G, aber man rechnet direkt nach, dass , also eine Translation ist, daher muss ihr Verschiebevektor von der Form . Da L eine Isometrie ist und Längen erhält, ist genauso lang wie , muss also auch einer der kürzestmöglichen Translationsvektoren sein, also . Man ergänzt nun zu einer Orthogonalbasis und überlegt sich aufgrund der Isometrieeigenschaften von L, dass gelten muss. Über den Existenz- und Eindeutigkeitssatz ergeben sich so alle möglichen linearen Anteile einer beliebigen Abbildung einer Bandornamentgruppe. So stellt man fest, dass es insgesamt vier mögliche Abbildungen gibt, also fünf mögliche Punktgruppen (nämlich die Gruppe aller Abbildungen und deren Untergruppen). Zur Rekonstruktion der Friesgruppen G überlegt man sich dann zu jeder Punktgruppe, welche Verschiebevektoren für eine Abbildung aus G in Frage kommen. Dabei stellt man fest: Enthält eine Punktgruppe eine Spiegelung an einer Geraden in Friesrichtung, so sind zwei Fälle zu unterscheiden:
- Die Friesgruppe selbst enthält eine Spiegelung
- Die Friesgruppe selbst enthält nur Schubspiegelungen
Diese Überlegung führt zu der Aufspaltung der Fälle 4 und 5 in zwei „Unterfälle“ 4.1 und 4.2 bzw. 5.1 und 5.2. Nachdem man durch die obigen Überlegungen alle mögliche Gruppentypen gefunden hat, zeigt man explizit durch Konstruktion einer geeigneten Abbildung, dass Gruppen, die zu gleichen Fällen gehören, zueinander ähnlich sind. Außerdem beweist man, dass Gruppen die zu verschiedenen Fällen gehören, einander nicht ähnlich sein können.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Nachfolgend einige Beispiele für jeden Typ einer Friesgruppe. Das dargestellte Fries weist dabei die entsprechende Friesgruppe als Symmetriegruppe auf. Die grauen Elemente gehören jeweils zu dem Muster, in schwarz sind Symmetrieelemente eingezeichnet: Punkte geben Inversionszentren an, gestrichelte Linien Spiegelachsen, durchgezogene oder strichpunktierte Linien echte Schubspiegelachsen, der Pfeil zeigt einen der beiden möglichen Friesvektoren an.
Das nachfolgende Bild zeigt ein Fries des Typs F5.1 (aus einem Bodenteppich):
Variablen und Begriffsverzeichnis[Bearbeiten | Quelltext bearbeiten]
Verzeichnis wichtiger im Artikel verwendeter Variablen:
| Symbol | Erläuterung |
|---|---|
| Eine Translation, Abbildung der Form | |
| Die Menge | |
| Friesrichtung | |
| E | Ein zweidimensionaler Vektorraum |
| Die Menge aller Isometrien von E | |
| Die Menge aller Translationen von G (Translationsgruppe) | |
| Abbildung der Form . v heißt Verschiebevektor, L linearer Anteil. |
Bandornamente in der Kunstethnologie[Bearbeiten | Quelltext bearbeiten]
Bandornamente werden in vielen Kulturen zur Dekoration verwendet. Beispielsweise kommen alle sieben Friesgruppen bei den Inka vor, aber drei der sieben Friesgruppen stellen 71 Prozent aller bekannten Funde dar. Sowohl im Königreich der Kuba als auch im Königreich Benin verwendeten Kunsthandwerker alle sieben Friesgruppen und zwölf der siebzehn Ornamentgruppen, aber in jeder Kultur wurden andere Symmetriegruppen zahlenmäßig bevorzugt.[2]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Erhard Quaisser: Diskrete Geometrie. Einführung, Probleme, Übungen. Spektrum Akademischer Verlag, Heidelberg u. a. 1994, ISBN 3-86025-309-3, 4.2. Die Friesgruppen (S. 42–52).
- Klaus Lamotke: Die Symmetriegruppen der ebenen Ornamente. In: Mathematische Semesterberichte. Band 52, Nr. 2, August 2005, S. 153–174, doi:10.1007/s00591-005-0092-y (Abschnitt 3).
- Harald Scheid, Wolfgang Schwarz: Elemente der Geometrie. 5. Auflage. Springer Spektrum, Berlin 2017, §4.2: Symmetrien und Ornamente, insbes. S. 139–148, doi:10.1007/978-3-662-50323-2_4 (ISBN 978-3-662-50322-5 (Print), ISBN 978-3-662-50323-2 (E-Book)).
- Dorothy K. Washburn, Donald W. Crowe: Symmetries of Culture. Theory and Practice of plane pattern Analysis. 3. Auflage. University of Washington Press, Seattle WA u. a. 1998, ISBN 0-295-97084-7, 4 One-Dimensional Patterns (S. 81-125).
- Mickaël Launay: Der große Roman der Mathematik. 2. Auflage. C. H. Beck Paperback, München 2021, ISBN 978-3-406-73955-2, S. 16–23 (Populärwissenschaftliche Einführung).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Udo Hebisch: Klassische Algebra. September 2009, (Achtung, abweichende Bezeichnungen).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Folgerung 2.3 aus Michael Klemm: Symmetrien von Ornamenten und Kristallen. Springer, Berlin u. a. 1982, ISBN 3-540-11644-3.
- ↑ Dorothy K. Washburn, Donald W. Crowe: Symmetries of Culture. Theory and Practice of plane pattern Analysis. 3rd printing. University of Washington Press, Seattle WA u. a. 1998, ISBN 0-295-97084-7, Chapter 4.3, S. 94–125.