Horizont

Der Horizont ist eine Linie, die den Himmel von der Erde abgrenzt.
Bei dem natürlichen Horizont hängt der Verlauf dieser Grenzlinie von Standort und Höhe des Beobachters sowie den örtlichen Gegebenheiten der umgebenden Landschaft ab, über dem Meer wird diese Linie auch Kimm genannt. Vom Horizont abhängige Beobachtungen, etwa des Sonnenaufgangs, lassen sich bei verschiedenen Standorten leichter vergleichen, wenn sie auf einen vereinfacht gedachten Horizont bezogen werden (Bezugshorizont).

Dieser ideale Horizont spannt eine Ebene auf, die rechtwinklig zur Zenit- oder Lotrichtung steht und als Horizontebene oder Horizontalebene bezeichnet wird. Eine waagerechte Ebene oder Linie wird häufig auch Horizontale genannt.
Der Ausdruck Gesichtskreis wurde im 17. Jahrhundert von Philipp von Zesen im Sinne einer Verdeutschung anstelle von Horizont eingeführt, wird heute aber nur noch selten mit dieser Bedeutung verwendet.[1]
Wortherkunft[Bearbeiten | Quelltext bearbeiten]
Das Wort Horizont[2] ist ein Lehnwort aus dem Lateinischen, das lateinische Wort horizon[3] wiederum ist entlehnt aus dem Altgriechischen. Es geht zurück auf ὁρίζων horízōn mit der Bedeutung „Grenzlinie“ – als Verkürzung des Ausdrucks ὁρίζων κύκλος horízōn kýklos „begrenzender Kreis“ oder „des Begrenzenden Kreis“[4] – gebildet zu ὁρίζειν horízein „begrenzen“, einer Ableitung von ὅρος hóros „Grenze“.[5]
Präzise Definitionen[Bearbeiten | Quelltext bearbeiten]

H H′ – astronomischer Horizont
C1 C2 C3 C4 – nautischer Horizont
B1 B2 B3 B4 – optischer Horizont
Der astronomische Horizont ist ebenfalls kreisförmig; hier ist er als Gerade dargestellt, wie er dem Betrachter beim Blick in eine bestimmte Richtung erscheint.
Genauer betrachtet sind einige Bedeutungen zu unterscheiden, die sich alle durch unterschiedliche Sichtweiten und scheinbare Entfernungen zum Horizont unterscheiden:
- Natürlicher oder Landschaftshorizont: die Grenzlinie zwischen Himmel und Erde, wie sie von den örtlichen Bedingungen (Landschaft, Berge, Stadtsilhouette) abhängt.
- Mathematischer Horizont oder astronomischer Horizont: die Schnittlinie der Sphäre der Himmelskugel mit jener Ebene, die im Beobachtungsort rechtwinklig zur Lotrichtung steht. Letztere ist nicht die Richtung zum Erdmittelpunkt, welche wegen der Erdabplattung um bis zu 0,2° von der Lotrichtung abweicht.
- Nautischer Horizont, Kimm(ung), Kimmlinie: der natürliche Horizont am Meer. Er liegt je nach Beobachterhöhe um die Kimmtiefe unter dem mathematischen Horizont.
- Optischer Horizont: durch die Lichtbrechung in der Lufthülle (terrestrische Refraktion) wird die Sichtweite größer und der Horizont in weiterer Entfernung gesehen.
- Radiohorizont: Radiowellen verhalten sich (abhängig von ihrer Wellenlänge, erst ab Ultrakurzwelle spricht man von quasioptischer Wellenausbreitung) ähnlich wie Licht. Die Brechung wird berücksichtigt durch einen größeren scheinbaren Erddurchmesser.
Die Horizontebene ist die Ebene des geometrischen Horizonts. Die Vertikale auf diese Ebene schneidet die Himmelssphäre in Zenit und Nadir.
Horizont in der Nautik, Kimmlinie[Bearbeiten | Quelltext bearbeiten]
Die Kimm ist die auf offenem Meer sichtbare Grenzlinie zwischen Wasser und Himmel. Auf sie beziehen sich Messungen von Höhenwinkeln, zum Beispiel mit einem Sextanten.
Wegen der Erdkrümmung – der mittlere Erdradius beträgt 6371 km, der Krümmungsradius der Erde liegt zwischen minimal 6334 km und 6400 km maximal – erscheint die Kimm umso tiefer unter dem mathematischen Horizont, je höher sich der Beobachter über dem Meeresspiegel befindet.
Daher müssen die Höhenwinkel um die Kimmtiefe verkleinert werden. Diese sogenannte Höhenbeschickung beträgt
(Kimmtiefe in Bogenminuten; Höhe des Beobachters in Metern).
Nach der DIN 13312 („Navigation; Begriffe, Abkürzungen …“) soll für die Kimmtiefe in der Seefahrt die Abkürzung „Kt“, im Englischen die Abkürzung „D“ (von dip of horizon), in der Luftfahrt die Abkürzung „Dip“ verwendet werden; als Formelzeichen wird für die Seefahrt k empfohlen.
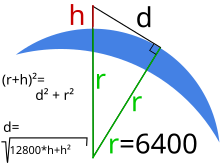
Die Distanz des Horizonts von einem Punkt mit der Höhe über der Erdoberfläche lässt sich geometrisch mit der Formel
berechnen, wobei der Krümmungsradius der Erde ist. Wird für der Wert eingesetzt, was etwa dem maximal möglichen Wert in Metern entspricht, ergibt sich für eine Beobachtungshöhe von 400 m:
- rund
Für Höhen , die sehr viel kleiner als der Erdradius sind , kann der Term gegenüber vernachlässigt werden; damit erhält man vereinfacht die folgende Näherungsformel[6]
Setzt man hier den mittleren Erdradius (6371 km) für ein, so erhält man die Horizontdistanz in Kilometern, bei Angabe der Höhe in Metern, mit der Faustformel:
Damit ergibt sich zum Beispiel für eine Beobachtungshöhe von 400 m:
Die geometrisch berechnete Distanz zum nautischen Horizont entspricht wegen der Lichtbrechung in der Erdatmosphäre aber nicht der Entfernung zum optischen Horizont. Abhängig von den Druck- und Temperaturbedingungen in der unteren Lufthülle kann die terrestrische Refraktion erheblich schwanken. Im Mittel liegt der scheinbare Erdradius bei circa 7680 km, der gesehene Horizont um rund ein Zehntel weiter entfernt als der geometrisch berechnete. Die Entfernung zum optischen Horizont lässt sich so abschätzen mit der Formel:
- ,
im Beispiel
Für Details und zusätzliche Beispiele siehe auch geodätische Sichtweite.
Horizont in Mathematik, Astronomie und Geodäsie[Bearbeiten | Quelltext bearbeiten]
Der Horizont im mathematischen Sinn ist ein Großkreis, der die Sphäre oder Himmelskugel in zwei gleiche Hälften teilt und dessen Pol der Zenit ist.
- Geometrischer Horizont
- ein Großkreis im oben erwähnten Sinn, der in der Astronomie zwei Bezugspunkte kennt:
- Geozentrischer (wahrer) Horizont: die horizontale Ebene geht durch den Erdmittelpunkt
- Topozentrischer (scheinbarer) Horizont (häufiger verwendet): durch einen Ort an der Erdoberfläche, beziehungsweise durch den Standpunkt des Beobachters. Der Unterschied im Höhenwinkel eines Gestirns entspricht der Parallaxe, während die Azimute dieselben sind.
Er ist die Basis des Horizontsystems – ein Koordinatensystem, in dem Gestirne und terrestrische Messpunkte durch Richtung (Azimut, Kurs) und Höhenwinkel angegeben werden. Senkrecht zum Horizont – also durch den Zenit – verlaufen die Vertikalkreise, von denen der Meridian genau in Nord-Süd-Richtung liegt.
- Horizont als Messbezug
Der Horizont ist der wichtigste Bezug für lokale Messungen. Die wichtigsten Geräte zu seiner Realisierung sind die Wasserwaage bzw. (genauer) die Röhrenlibelle, ferner Höhenkompensatoren und andere Pendelkörper, elektronische Neigungssensoren und bisweilen Flüssigkeits- bzw. Quecksilberspiegel.
Die Messung der Horizontalen erfolgt mit Nivelliergerät, die Aufstellung von Messinstrumenten wird Horizontieren genannt.
Horizont in der Kunst[Bearbeiten | Quelltext bearbeiten]

Der Begriff Horizont wird in der Kunst vielfach als Sinnbild für Sehnsüchte und Utopien verwendet. Beispiele dafür sind das Lied Horizont von Udo Lindenberg, der Roman Der verlorene Horizont von James Hilton oder das Bild Forgotten Horizon von Salvador Dalí. In den Werken des Künstlers Jens Lausen spielt der Horizont eine zentrale Rolle.
Die Gruppe Knorkator thematisiert in ihrem Lied Wie weit ist es bis zum Horizont die Berechnung der Entfernung bis zum Horizont über den Satz des Pythagoras.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Dämmerung, Sonnenaufgang, Sonnenuntergang
- Künstlicher Horizont – Messinstrument zur Ermittlung der Horizontalen
- Horizontproblem, Grundproblem der Kosmologie
- Horizontastronomie
- Horizontalpendel
- Horizont (Geologie)
Literatur[Bearbeiten | Quelltext bearbeiten]
- Albrecht Koschorke: Die Geschichte des Horizonts. Grenze und Grenzüberschreitung in literarischen Landschaftsbildern. Suhrkamp, Frankfurt am Main 1990, ISBN 3-518-58064-7.
- Ulrich Scharnow: Lexikon Seefahrt. 5. Auflage. Transpress VEB Verlag für Verkehrswesen, Berlin 1988, ISBN 3-344-00190-6, S. 277.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise und Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ siehe Duden online: Gesichtskreis
- ↑ vergleiche Duden online: Horizont
- ↑ horizontis im Genitiv; C. Lewis, C. Short: A Latin Dictionary. Oxford 1879, horizon.
- ↑ so auch ὁρίζοντος κύκλος horízontos kýklos bei Aristoteles, siehe Liddell-Scott-Jones: A Greek-English Lexicon. 9. Ausgabe, Clarendon Press, Oxford 1940 [2003], ὁρίζων bzw. Stichwort ὁρίζοντος, auf Perseus.
- ↑ Friedrich Kluge, Elmar Seebold: Etymologisches Wörterbuch der deutschen Sprache. 25. Auflage. 2011 (Lemma Horizont in der Google-Buchsuche).
- ↑ Diese Näherung gilt auch für auf 10 km Höhe fliegende Flugzeuge.

















