Matching (Graphentheorie)
Die Theorie um das Finden von Matchings in Graphen ist in der diskreten Mathematik ein umfangreiches Teilgebiet, das in die Graphentheorie eingeordnet wird.
Folgende Situation wird dabei betrachtet: Gegeben sei eine Menge von Dingen und zu diesen Dingen Informationen darüber, welche davon einander zugeordnet werden könnten. Ein Matching (in der Literatur manchmal auch Paarung) ist dann als eine solche Auswahl aus den möglichen Zuordnungen definiert, die kein Ding mehr als einmal zuordnet.
Die am häufigsten gestellten Fragen in dieser Situation sind dann die folgenden:
- Wie findet man ein Matching, das eine maximale Anzahl[A 1] an Dingen einander zuordnet?
Dieses Problem ist das klassische Matchingproblem. - Gibt es ein Matching, das alle Dinge zuordnet? Wenn ja, wie viele?
Solche Matchings heißen perfektes Matching. Die Anzahl der perfekten Matchings in einem Graphen wird meistens mit notiert. - Angenommen, man könnte quantifizieren „wie wichtig“ (oder „teuer“) die einzelnen Zuordnungen wären: Wie findet man dann ein Matching, das eine maximale Zahl von Dingen zuordnet und dabei ein möglichst großes (oder kleines) Gewicht hat?
Dieses Problem heißt gewichtetes Matchingproblem. Zwischen einer Maximierungs- und einer Minimierungsaufgabe wird hier oftmals nicht unterschieden: Indem man bei allen Gewichten (Kosten) das Vorzeichen vertauscht, kann man beide Probleme ohne nennenswerten Aufwand ineinander überführen. - Angenommen, man hätte genau zwei Klassen von Dingen und angenommen, man wüsste, dass es ausschließlich zwischen diesen Klassen mögliche Zuordnungen gibt. Werden die Probleme 1–3 dadurch einfacher?
Dieses Problem heißt bipartites (gewichtetes) Matchingproblem und ist ein viel diskutierter Spezialfall. - Kann man anderes Wissen, das man über die Struktur der möglichen Zuordnungen hat, ähnlich wie in 4 geschickt benutzen, um die Probleme 1–3 effizienter zu lösen?
Die Theorie um die Matchings untersucht möglichst effiziente Lösungsverfahren dieser Probleme, klassifiziert diese nach ihrer Laufzeit mit den Methoden der Komplexitätstheorie und stellt Beziehungen dieser Probleme zueinander und zu anderen Problemen in der Mathematik her.
Definitionen[Bearbeiten | Quelltext bearbeiten]
-
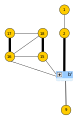
Ein einfacher Graph mit einem nicht erweiterbaren Matching (maximal matching)
-
Derselbe Graph mit einem perfekten (wie auch größtmöglichen) Matching
Das oben beschriebene Problem lässt sich wie folgt formalisieren. Gegeben sei ein endlicher, ungerichteter Graph . Eine Menge heißt Matching, wenn keine zwei Kanten aus einen Knoten gemeinsam haben. Ein Matching heißt
- nicht erweiterbar (engl. maximal matching)
- falls es keine Kante derart gibt, dass ein Matching ist. Maximale Matchings sind im Vergleich zu den folgenden Begriffen sehr einfach zu berechnen.
- größtmöglich (engl. maximum matching)
- falls als Menge eine maximale Kardinalität unter allen Matchings von hat. Maximum-Matchings sind maximal. Die Mächtigkeit eines Maximum-Matchings wird Matchingzahl genannt und mit notiert.
- perfekt
- falls gilt, d. h. wenn jeder Knoten gematcht wurde. Perfekte Matchings sind Maximum-Matchings und damit auch maximal. Perfekte Matchings können als 1-Faktoren eines Graphen, das heißt 1-reguläre aufspannende Teilgraphen, aufgefasst werden. Dieser Auffassung folgend spricht man auch von faktorisierbaren Graphen, wenn sie einen 1-Faktor besitzen.[1]
Definitionen (gewichtetes Matching-Problem)[Bearbeiten | Quelltext bearbeiten]
Für das gewichtete Matchingproblem spielt eine Kostenfunktion eine Rolle. Ein Matching heißt
- maximal
- falls maximal unter allen Matchings von ist.
- minimal maximal
- falls minimal unter allen maximalen Matchings ist.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
In jedem Graphen ohne isolierte Knoten ist die Summe der übereinstimmenden Matchingzahl und der Kantenüberdeckungszahl gleich der Anzahl der Knoten. Wenn es ein perfektes Matching gibt, sind sowohl die Matchingzahl als auch die Kantenüberdeckungszahl gleich .
Wenn und zwei nicht erweiterbare Matchings sind, dann gilt und . Das liegt daran, dass jede Kante in höchstens mit zwei Kanten in benachbart sein kann, weil ein Matching ist. Außerdem grenzt jede Kante in an eine Kante in , weil nicht erweiterbar ist. Daher gilt
Daraus folgt
also .
Wenn der Graph zum Beispiel ein Pfad mit 3 Kanten und 4 Knoten ist, beträgt die Größe eines minimalen maximalen Matchings 1 und die Größe eines perfekten Matchings beträgt 2.
Kombinatorik[Bearbeiten | Quelltext bearbeiten]
Die Anzahl der Matchings mit Kanten für bestimmte Graphen zeigt die folgende Tabelle:[2]
| Anzahl der Matchings mit k Kanten | |
|---|---|
| vollständiger Graph | |
| vollständig bipartiter Graph | |
| Kreisgraph | |
| Pfadgraph | |
Historisches[Bearbeiten | Quelltext bearbeiten]

Als eine der frühesten[3][4] systematischen Untersuchungen von Matchings wird ein Artikel von Julius Petersen angeführt, der 1891 über „Die Theorie der regulären graphs“ schrieb.[5] Er untersuchte ein Zerlegungsproblem aus der Algebra, das David Hilbert 1889[6] gestellt hatte, indem er es als Graphenproblem formulierte.[3] Letztlich bewies er darin folgendes:
- Für alle Zahlen kann jeder -reguläre Graph in disjunkte -Faktoren zerlegt werden. (1)
- Jeder kubische, zusammenhängende Graph mit weniger als drei Brücken besitzt ein perfektes Matching. (2)
Die Tatsache (2), bekannt als Satz von Petersen, lässt sich auch als eine leichte Verallgemeinerung des Eulerkreisproblems formulieren.[A 2]
Rückblickend erscheinen Petersens Argumente, mit denen er das Obige bewies, kompliziert und umständlich.[7] Bei der weiteren Untersuchung etwa durch Brahana 1917[8], Errera 1922[9] und Frink 1926[10] sowie zusammenfassend durch Kőnig 1936[11] wurden aber viele Methoden der modernen Graphentheorie entwickelt oder zuerst systematisch formuliert. Petersens Denkansatz wurde dann von Bäbler 1938[12] 1952[13] und 1954[14] sowie von Gallai 1950[15], Belck 1950[16] und schließlich Tutte auf andere reguläre Graphen übertragen.
In modernen Lehrbüchern und Vorlesungen tauchen Petersens ursprüngliche Resultate, wenn überhaupt, meist nur noch als Folgerungen aus den Resultaten von Tutte oder Hall auf. Im Buch von Diestel folgt die erste Aussage aus dem Heiratssatz von Hall.[7] Die zweite Aussage wird auf den Satz von Tutte zurückgeführt.[17]
Bipartite Matchings[Bearbeiten | Quelltext bearbeiten]
Eines dieser frühen Resultate betrifft bipartite Graphen, die sich in der Folge als ein sehr natürlicher und aus heutiger Sicht für die Praxis zentraler Spezialfall herausgestellt haben. Kőnig und Egerváry untersuchten beide unabhängig voneinander das bipartite Matchingproblem und das Knotenüberdeckungsproblem und fanden dabei heraus, dass beide Probleme in dem folgenden Sinn äquivalent sind:
- Die Größe einer minimalen Knotenüberdeckung und eines maximum-Matching stimmen auf bipartiten Graphen überein. (3)
Dieser Satz wird meistens Kőnig zugeschrieben oder Min-Max-Theorem bzw. Dualitätssatz genannt. Beide bewiesen die Aussage für endliche Graphen. Aharoni bewies 1984 die Aussage für überabzählbar unendliche Graphen.[18] Ein elementarer Beweis von (3) findet sich in Lovász & Plummer 43, der von den meisten Lehrbüchern übernommen wurde. Bondy & Murty 200 führt den Satz auf ein Resultat der linearen Programmierung zurück: Ist die Inzidenzmatrix des Graphen , dann lassen sich maximum Matchings als Lösungen von folgendem ganzzahligen linearen Programm auffassen:
Dabei ist der Einsvektor bestehend aus lauter Einsen. Das Programm des Knotenüberdeckungsproblems hat folgende Gestalt:
Diese Programme haben eine sogenannte primal-dual-Gestalt. Für Programme von dieser Gestalt wird in der Theorie der linearen Programme gezeigt, dass sie in ihren Optima übereinstimmen. Für bipartite Graphen lässt sich außerdem leicht zeigen, dass total unimodular ist, was in der Theorie der ganzzahligen linearen Programme ein Kriterium für die Existenz einer optimalen Lösung der Programme mit Einträgen nur aus (und damit in diesem speziellen Fall sogar aus ) ist, also genau solchen Vektoren, die auch für ein Matching bzw. für eine Knotenüberdeckung stehen können. Dieser Primal-Dual-Ansatz der linearen Programme scheint zunächst wenig mit der Matching-Theorie zu tun zu haben, stellt sich aber als einer der fruchtbarsten Ansätze zur effizienten Berechnung von Matchings, insbesondere im gewichteten Fall, heraus.
Es gibt eine ganze Vielzahl von Sätzen, die zum Satz von König äquivalent sind.[19][20][21] Darunter der Satz von Birkhoff und von Neumann, der Satz von Dilworth und das Max-Flow-Min-Cut-Theorem für bipartite Graphen. Für die Matchingtheorie am interessantesten ist folgende Bedingung, die Hall 1935[22] angab, um bipartite Graphen mit perfektem Matching zu charakterisieren. Dieser Charakterisierungssatz ist ebenfalls äquivalent zum Satz von König.
- Ein bipartiter Graph mit Knotenpartitionen und o.B.d.A hat genau dann ein perfektes Matching, wenn für jede Auswahl von Knoten gilt: . Dabei ist die Nachbarschaftsmenge von . (4)
Aus (4) folgt schnell, dass sich unter den bipartiten Graphen genau alle regulären Graphen -faktorisieren lassen[23] und die Aussage (1) von Petersen lässt elegant auf diese Folgerung zurückführen.[7] Eine Verallgemeinerung dieses Resultats liefert eine Formel für die Größe eines maximum Matchings, die sogenannte König-Ore Formel:[24][25]
Lösungsverfahren[Bearbeiten | Quelltext bearbeiten]
Eingabe mit einem beliebigen Matching 1. repeat 2. suche verbessernden Pfad 3. Falls gefunden: Augmentiere entlang . 4. until Suche nach verbesserndem Pfad war erfolglos Ausgabe mit maximum Matching |
Viele der folgenden Konzepte spielen in fast allen Lösungsverfahren von Matchingproblemen eine Rolle. Ist ein Graph mit einem Matching gegeben, dann heißt ein Knoten von frei (in der Literatur auch ungepaart, exponiert, verfügbar …), falls er zu keiner Kante in inzident ist. Andernfalls heißt der Knoten gesättigt. Ein Pfad in heißt alternierend, falls dieser abwechselnd Kanten aus und aus enthält. Falls dieser Pfad in einem freien Knoten beginnt und endet, heißt der Pfad verbessernd oder auch augmentierend. Die letzte Bezeichnung kommt von der Tatsache, dass durch [A 3] ein größeres Matching als liefert. Folgendes grundlegendes Resultat von Berge 1957[26] motiviert das Studium von augmentierenden Pfaden.
- Ein Matching ist genau dann Maximum, wenn es keinen verbessernden Pfad in bezüglich gibt.
Diese Bezeichnungen entsprechen genau der Sprache, die auch bei der Behandlung von Flüssen in Netzwerken gebraucht wird. Das ist kein Zufall, denn Matchingprobleme lassen sich in der Sprache der Netzwerktheorie formulieren und mit den dort entwickelten Verfahren lösen. Im bipartiten Fall ist diese Zurückführung, wie das folgende Beispiel zeigt, sogar fast trivial. Gegeben ein Graph mit Knotenmenge . Konstruiere ein Netzwerk . Dabei ist und . Außerdem ist die Fortsetzung von der Kostenfunktion , die alle neuen Kanten mit Inf[A 4] belegt.
Mit dem Satz von Berge lässt sich auch gleich ein Algorithmus (I) zum Finden von maximum Matchings angeben.[27] Weil jeder verbessernde Pfad zu einem gegebenen Matching einen weiteren Knoten matcht und maximal Knoten zu matchen sind, beschränkt sich die Zahl der Schleifendurchläufe asymptotisch durch . Eine sehr naive Methode zum Finden verbessernder Pfade stellen sogenannte Graph Scans dar, etwa eine Breitensuche (BFS) mit einer Laufzeit von . Ferner ist , weil der Graph bipartit ist und damit ist die angegebene Methode in .
Einer der frühesten Beiträge zum Berechnen von Maximum-Matchings, der über die oben angeführte naive Methode hinausgeht, war der Algorithmus von Hopcroft und Karp 1973.[28] Die Grundidee folgt dem Algorithmus von Dinic (mit dem das Problem mit derselben asymptotischen Laufzeit gelöst werden kann[29]), der in jeder Phase, wo der Algorithmus nach einem verbessernden Pfad sucht (Zeile 2), möglichst kurze Pfade und nach Möglichkeit „mehrere gleichzeitig“ sucht.
Alt, Blum, Mehlhorn & Paul 1991[30] schlagen eine Verbesserung von Hopcroft & Karp vor, indem sie ein Scanningverfahren für Adjazenzmatrizen nach Cheriyan, Hagerup, and Mehlhorn 1990[31] anwenden. Eine einfache Beschreibung der Methode findet sich auch in Burkard, Dell’Amico & Martello 47 ff. Feder und Motwani 1991[32] haben eine Methode vorgeschlagen, die auf der Zerlegung von in bipartite Cliquen beruht und erreichen damit eine asymptotische Laufzeit von . Eine Methode, die nicht auf der Idee augmentierender Pfade beruht, sondern sogenannte „starke Spannbäume“ benutzt, haben Balinski & Gonzalez 1991[33] vorgeschlagen und erreichen damit eine Laufzeit von .
Programmierung[Bearbeiten | Quelltext bearbeiten]
Das folgende Beispiel in der Programmiersprache C# zeigt ein Programm, das die Matchingzahl für einen bipartiten Graphen bestimmt. Der bipartite Graph wird als zweidimensionales Array vom Datentyp bool (Boolesche Variable) deklariert. Wenn zwei Knoten verbunden sind, wird der Wert true gespeichert, wenn nicht, wird der Wert false gespeichert. Die Methode BipartiteMatching, die feststellt, ob es ein passendes Matching gibt, verwendet einfache Rekursion. Bei der Ausführung des Programms wird die Methode Main verwendet, die die Matchingzahl auf der Konsole ausgibt.[34]
using System;
class Program
{
// Diese Methode verwendet Tiefensuche und stellt fest, ob es ein Matching mit dem Knoten mit startIndex gibt
bool BipartiteMatching(bool[,] bipartiteGraph, int startIndex, bool[] visitedIndexes, int[] matchedIndexes, int n)
{
for (int targetIndex = 0; targetIndex < n; targetIndex++) // for-Schleife, die alle Indexe der Zielknoten durchläuft
{
if (bipartiteGraph[startIndex, targetIndex] && !visitedIndexes[targetIndex]) // Wenn die Knoten mit startIndex und targetIndex im bipartiten Graphen verbunden sind und Zielknoten nicht besucht ist
{
visitedIndexes[targetIndex] = true; // Setzt den Zielknoten auf besucht
// Wenn der Knoten mit targetIndex nicht zugeordnet ist, wird er dem Knoten mit startIndex zugeordnet. Wenn der Knoten mit targetIndex auf besucht gesetzt ist, wird er im rekursiven Aufruf nicht erneut zugeordnet.
if (matchedIndexes[targetIndex] == -1 || BipartiteMatching(bipartiteGraph, matchedIndexes[targetIndex], visitedIndexes, matchedIndexes, n)) // Rekursiver Aufruf der Methode mit dem Nachbarknoten als Startknoten
{
matchedIndexes[targetIndex] = startIndex;
return true;
}
}
}
return false;
}
// Diese Methode gibt die Matchingzahl des bipartiten Graphen zurück
int GetMatchingNumber(bool[,] bipartiteGraph, int m, int n)
{
int[] matchedIndexes = new int[n]; // Array, das die Indexe der zugeordneten Knoten speichert
for (int i = 0; i < n; ++i) // for-Schleife, die alle Indexe der Zielknoten durchläuft
{
matchedIndexes[i] = -1; // Setzt alle Knoten auf nicht zugeordnet
}
int matchingNumber = 0; // Zählt die Anzahl der Matchings
for (int startIndex = 0; startIndex < m; startIndex++) // for-Schleife, die alle Indexe der Startknoten durchläuft
{
bool[] visitedIndexes = new bool[n]; // Array, das die Indexe der besuchten Knoten speichert
for (int i = 0; i < n; ++i) // for-Schleife, die alle Indexe der Zielknoten durchläuft
{
visitedIndexes[i] = false; // Setzt alle Knoten auf nicht besucht
}
if (BipartiteMatching(bipartiteGraph, startIndex, visitedIndexes, matchedIndexes, n)) // Untersucht, ob es ein Matching mit dem Knoten mit startIndex gibt
{
matchingNumber++;
}
}
return matchingNumber;
}
// Hauptmethode, die das Programm ausführt
public static void Main()
{
// Erzeugt einen bipartiten Graphen
bool[,] bipartiteGraph = new bool[,]
{{false, true, true, false, false, false},
{true, false, false, true, false, false},
{false, false, true, false, false, false},
{false, false, true, true, false, false},
{false, false, false, false, false, false},
{false, false, false, false, false, true}};
Program program = new Program();
Console.WriteLine("Die Matchingzahl des bipartiten Graphen ist " + program.GetMatchingNumber(bipartiteGraph, 6, 6) + "."); // Ausgabe auf der Konsole
Console.ReadLine();
}
}
Allgemeiner Fall[Bearbeiten | Quelltext bearbeiten]
Satz von Tutte[Bearbeiten | Quelltext bearbeiten]
Während Charakterisierungen von Matchings und effiziente Algorithmen zum Bestimmen relativ schnell nach der Formulierung von Matchings als Problem gefunden wurden, dauerte es bis 1947 bis Tutte[35] eine Charakterisierung für perfekte Matchings in allgemeinen Graphen formulieren und beweisen konnte. Aus diesem tiefliegenden Resultat lassen sich alle bisher besprochenen vergleichsweise leicht herleiten.[36] Tutte benutzt die einfache Tatsache, dass eine Komponente mit ungerader Knotenzahl in einem Graphen kein perfektes Matching haben kann. Wenn also eine Knotenmenge so gefunden werden kann, dass mehr ungerade Komponenten als Knoten hat, dann müsste für ein perfektes Matching aus jeder solcher Komponente wenigstens ein Knoten mit einem Knoten aus gematcht werden und das kann nicht sein. Es stellt sich heraus, dass die Existenz einer solchen Menge Graphen ohne perfektes Matching nicht nur beschreibt, sondern charakterisiert:
- Ein Graph hat genau dann ein perfektes Matching, wenn für jede Menge gilt: . ( gibt die Anzahl der ungeraden Komponenten eines Graphen an.) (5)
Eine solche Menge heißt Tutte-Menge und die Bedingung in (5) heißt Tutte-Bedingung. Dass sie notwendig für die Existenz perfekter Matching ist, wurde schon skizziert und es gibt mittlerweile viele Beweise dafür, dass die Bedingung hinreichend ist: Tuttes ursprünglicher Beweis formulierte das Problem als ein Matrix-Problem und benutzte die Idee der pfaffschen Determinante.[35] Elementare Abzählargumente wurden relativ rasch danach veröffentlicht, wie in Maunsell 1952,[37] Tutte 1952,[38] Gallai 1963,[39] Halton 1966[40] oder Balinski 1970.[41] Andere Beweise, wie Gallai 1963,[39] Anderson 1971[42] oder Marder 1973[43] verallgemeinern den Satz (4) von Hall systematisch. Ferner gibt es Beweise aus der Perspektive der Graphentheorie, die die Struktur von Graphen betrachten, die selbst kein Perfektes Matching besitzen, doch falls eine Kante ergänzt wird, hat der resultierende Graph ein solches. Diesen Ansatz verfolgen etwa Hetyei 1972[44] oder Lovász 1975.[45]
Algorithmus von Edmonds[Bearbeiten | Quelltext bearbeiten]
Der erste Polynomialzeitalgorithmus für das klassische Matchingproblem stammt von Jack Edmonds (1965).[47] Die Grundstruktur der Methode entspricht Algorithmus (I): Sie sucht verbessernde Pfade und gibt ein maximum Matching zurück, falls kein solcher gefunden werden kann. Einen verbessernden Pfad zu finden, stellt sich hier aber als schwieriger heraus als im bipartiten Fall, weil einige neue Fälle auftreten können. Edmonds Suchmethode konstruiert nach und nach einen alternierenden Wald. Das ist ein kreisfreier Graph mit so vielen Zusammenhangskomponenten wie es freie Knoten gibt. Jeder freie Knoten ist Wurzel eines Baumes und ist so konstruiert, dass für alle anderen Knoten der eindeutig bestimmte --Pfad ein alternierender Pfad ist. Ein Knoten in heißt dann innen oder ungerade, falls und andernfalls außen oder gerade. sei hier die Distanzfunktion in , gebe also die Länge des eindeutig bestimmten --Pfades an.
Es genügt die Betrachtung auf die Konstruktion eines alternierenden Baumes zu reduzieren. Falls diese Konstruktion keinen augmentierenden Pfad findet, wird sie mit einem neuen freien Knoten reinitialisiert und alle bereits betrachteten Kanten werden ignoriert. Existiert kein freier Knoten mehr, dann existiert auch kein augmentierender Pfad. Diesen alternierenden Baum konstruiert Edmonds, indem er ausgehend von einem freien Knoten nach und nach alle Kanten hinzufügt oder ignoriert. Dabei können für eine neue Kante ( gehöre bereits zum Baum) folgende Fälle auftreten:
- Wenn ein innerer Knoten ist, können nur Kanten zu hinzugefügt werden, weil alternierend werden soll. Diese Kante ist eindeutig durch gegeben.
- Falls ein äußerer Knoten ist, dann kann …
- frei sein und noch nicht in . Dann ist der --Pfad augmentierend.
- gepaart sein und weder noch ist in . Dann können und zu hinzugefügt werden.
- bereits in als innerer Knoten enthalten sein. Damit schließt einen geraden Kreis. Diese Kanten können ignoriert werden.[48]
- bereits in als ein äußerer Knoten enthalten sein. Dann schließt einen ungeraden alternierenden Kreis ; eine sogenannte Blüte. Edmonds zieht die Knoten in zu einem Pseudoknoten zusammen mit den Inzidenzen aller Knoten aus . (Diese Operation lässt sich auch beschreiben als „Bildung des Quotientengraphen“ ) Er reinitialisiert dann die Suche in und gibt ein Verfahren an, einen dort gefundenen augmentierenden Pfad zu einem augmentierenden Pfad in zu liften.
Blüten können, anders als bei Fall , nicht ignoriert werden.[49] Der Knoten, der die Blüte mit dem Baum verbindet, lässt sich in das Schema der inneren und äußeren Knoten nicht einordnen. Die naheliegende Idee, ihn als „sowohl innen als auch außen“ zu behandeln führt zu einem falschen Algorithmus.[50] Die Behandlung von Blüten mit Kontraktion ist neben dem Ansatz von Berge die zentrale Idee von Edmonds’ Algorithmus und Grundlage vieler späterer Verfahren. Bipartite Graphen enthalten keine ungeraden Kreise und damit auch keine Blüten. Edmonds’ Algorithmus reduziert sich daher im bipartiten Fall auf die Methode von Munkres.
Man kann ablesen, dass die skizzierte Methode von Edmonds einen Aufwand von hat. In Fall reinitialisiert Edmonds die Suche und verwirft damit den bereits geleisteten Suchaufwand. Gabow 1976[51] und Lawler haben eine naive Implementierung vorgeschlagen, die den Suchaufwand nicht verwirft und eine Laufzeit von erreicht. Das Beispiel folgt bereits dieser Methode.
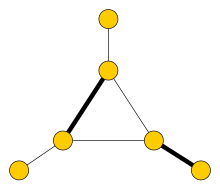
- Beispiel zu Edmonds
-
Der reduzierte Graph .
-
mit einer weiteren Blüte .
-
Der weiter reduzierte Graph
-
Von wird der freie Knoten gefunden, der nach Fall in den augmentierenden Pfad schließt. Die Liftung dieses Pfades liefert zunächst in , der aber auch schon in selbst liegt.
Literatur[Bearbeiten | Quelltext bearbeiten]
- M. D. Plummer, L. Lovász: Matching Theory (= Annals of Discrete Mathematics). 1. Auflage. Elsevier Science und Akadémiai Kiadó Budapest, Budapest 1986, ISBN 0-444-87916-1.
- Reinhard Diestel: Graphentheorie. 3., neu bearb. und erw. A. Auflage. Springer, Berlin 2006, ISBN 3-540-21391-0 (diestel-graph-theory.com).
- Dieter Jungnickel: Graphs, Networks and Algorithms (= Algorithms and Computation in Mathematics. Band 5). 3. Auflage. Springer, 2007, ISBN 978-3-540-72779-8.
- Guizhen Liu, Qinglin Roger Yu: Graph Factors and Matching Extensions. 1. Auflage. Springer, Beijing 2009, ISBN 978-3-540-93951-1.
- Alexander Schrijver: Combinatorial Optimization – Polyhedra and Efficiency (= Algorithms and Combinatorics. A). Springer, Amsterdam 2003, ISBN 3-540-44389-4.
- U.S.R. Murty, Adrian Bondy: Graph Theory (= Graduate Texts in Mathematics). Springer, 2008, ISBN 978-1-84996-690-0 (springer.com).
- Mauro Dell’Amico, Silvano Martello, Rainer Burkard: Assignment Problems (Revised reprint). Society for Industrial and Applied Mathematics, Philadelphia 2012, ISBN 978-1-61197-222-1 (assignmentproblems.com).
- David S. Johnson: Network Flows and Matching: First Dimacs Implementation Challenge. American Mathematical Society, 1993, ISBN 0-8218-6598-6.
- Eugene Lawler: Combinatorial Optimization: Networks and Matroids. Dover Publications, Rocquencourt 1976, ISBN 0-03-084866-0.
- Historisch
- Dénes Kőnig: Theorie der endlichen und unendlichen Graphen – kombinatorische Topologie der Streckenkomplexe. (= Teubner Archiv zur Mathematik). 1. Auflage 1986. Teubner Verlagsgesellschaft, Leipzig 1936, ISBN 3-322-00303-5.
- E. Keith Lloyd, Robin J. Wilson, Norman L. Biggs: Graph Theory 1736–1936. Oxford University Press, USA, 1999, ISBN 0-19-853916-9.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Yu & Liu 4.
- ↑ Wolfram MathWorld: Matching
- ↑ a b Lovász & Plummer xi.
- ↑ Yu & Liu 3.
- ↑ Julius Petersen: Die Theorie der regulären graphs. In: Acta Mathematica. 15. Jahrgang, 1891, S. 193–220, doi:10.1007/BF02392606.
- ↑ David Hilbert: Über die Endlichkeit des Invariantensystems für binäre Grundformen. In: Mathematische Annalen. 33. Jahrgang, Nr. 2, 1889, S. 223–226.
- ↑ a b c Reinhard Diestel: Graphentheorie. 3., neu bearb. und erw. A. Auflage. Springer, Berlin, 2006, ISBN 3-540-21391-0, S. 43 (diestel-graph-theory.com).
- ↑ Henry Roy Brahana: A Proof of Petersen’s Theorem. In: The Annals of Mathematics. 19. Jahrgang, Nr. 1, 1917, ISSN 0003-486X, S. 59–63, doi:10.2307/1967667.
- ↑ Alfred Errera: Une demonstration du théorème de Petersen. In: Mathesis. 36. Jahrgang, 1922, S. 56–61.
- ↑ Orrin Frink: A Proof of Petersen’s Theorem. In: The Annals of Mathematics. 27. Jahrgang, Nr. 4, 1926, ISSN 0003-486X, S. 491–493, doi:10.2307/1967699.
- ↑ Dénes Kőnig: Theorie der endlichen und unendlichen Graphen; kombinatorische Topologie der Streckenkomplexe. 1936.
- ↑ Fridolin Bäbler: Über die Zerlegung regulärer Streckenkomplexe ungerader Ordnung. In: Commentarii Mathematici Helvetici. 10. Jahrgang, Nr. 1, 1938, ISSN 0010-2571, S. 275–287, doi:10.1007/BF01214296.
- ↑ Fridolin Bäbler: Bemerkungen zu einer Arbeit von Herrn R. Cantoni. In: Commentarii Mathematici Helvetici. 26. Jahrgang, 1952, ISSN 0010-2571, S. 117–118 (digizeitschriften.de).
- ↑ Fridolin Bäbler: Über den Zerlegungssatz von Petersen. In: Commentarii Mathematici Helvetici. 28. Jahrgang, Nr. 1, 1954, ISSN 0010-2571, S. 155–161, doi:10.1007/BF02566927.
- ↑ Tibor Gallai: On factorization of graphs. In: Acta Mathematica Academiae Scientiarum Hungaricae. 1. Jahrgang, 1950, ISSN 0236-5294, S. 133–153.
- ↑ Hans-Boris Belck: Reguläre Faktoren von Graphen. In: Journal für die reine und angewandte Mathematik (Crelles Journal). 1950. Jahrgang, Nr. 188, 1950, ISSN 0075-4102, S. 228–252, doi:10.1515/crll.1950.188.228.
- ↑ Reinhard Diestel: Graphentheorie. 3., neu bearb. und erw. A. Auflage. Springer, Berlin, 2006, ISBN 3-540-21391-0, S. 45 (diestel-graph-theory.com).
- ↑ Ron Aharoni: Kőnig’s Duality Theorem for Infinite Bipartite Graphs. In: Journal of the London Mathematical Society. s2-29. Jahrgang, Nr. 1, 1984, ISSN 0024-6107, S. 1–12, doi:10.1112/jlms/s2-29.1.1.
- ↑ Lovász & Plummer 5-40.
- ↑ Notizen zu einem Vortrag von Robert D. Borgersen: Equivalence of seven major theorems in combinatorics. (PDF; 66 kB). November 26, 2004.
- ↑ K. Jacobs: Der Heiratssatz. In: Selecta Mathematica I. 1969, S. 103–141.
- ↑ Philip Hall: On representatives of subsets. In: Journal of London Mathematics Society. 10. Jahrgang, 1935, S. 26–30.
- ↑ Jungnickel 216.
- ↑ Yu & Liu 9.
- ↑ Bondy & Murty 422.
- ↑ Claude Berge: Two theorems in graph theory. In: Proceedings of the National Academy of Sciences. 43. Jahrgang, Nr. 9, 15. September 1957, S. 842–844 (pnas.org [PDF]).
- ↑ Aus didaktischen Gründen sehr stark vereinfacht nach Burkard, Dell’Amico & Martello 38. In der Referenz ist die Methode zum Finden eines verbessernden Pfades wesentlich detaillierter angegeben.
- ↑ John E. Hopcroft, Richard M. Karp: An Algorithm for Maximum Matchings in Bipartite Graphs. In: SIAM Journal on Computing. 2. Jahrgang, Nr. 4, 1973, ISSN 0097-5397, S. 225–231, doi:10.1137/0202019 (englisch).
- ↑ Shimon Even, Robert E. Tarjan: Network flow and testing graph connectivity. In: SIAM Journal on Computing. 4. Jahrgang, Nr. 4, 1975, ISSN 0097-5397, S. 507–518, doi:10.1137/0204043 (englisch).
- ↑ H. Alt, N. Blum, K. Mehlhorn, M. Paul: Computing a maximum cardinality matching in a bipartite graph in time . In: Information Processing Letters. 37. Jahrgang, Nr. 4, 1991, ISSN 0020-0190, S. 237–240, doi:10.1016/0020-0190(91)90195-N (englisch).
- ↑ Joseph Cheriyan, Torben Hagerup, Kurt Mehlhorn: Automata, Languages and Programming. Band 443. Springer-Verlag, Berlin/Heidelberg 1990, ISBN 3-540-52826-1, Can a maximum flow be computed in time?, S. 235–248 (englisch).
- ↑ Tomás Feder, Rajeev Motwani: Clique partitions, graph compression and speeding-up algorithms. twenty-third annual ACM symposium on Theory of computing. In: Proceedings of the twenty-third annual ACM symposium on Theory of computing. ACM, New York 1991, ISBN 0-89791-397-3, S. 123–133, doi:10.1145/103418.103424 (englisch).
- ↑ M. L Balinski, J. Gonzalez: Maximum matchings in bipartite graphs via strong spanning trees. In: Networks. 21. Jahrgang, Nr. 2, 1991, ISSN 1097-0037, S. 165–179, doi:10.1002/net.3230210203 (englisch).
- ↑ GeeksforGeeks: Maximum Bipartite Matching
- ↑ a b W. T Tutte: The factorization of linear graphs. In: Journal of the London Mathematical Society. 1. Jahrgang, Nr. 2, 1947, S. 107.
- ↑ Lovász & Plummer 84.
- ↑ F. G. Maunsell: A note on Tutte’s paper “The factorization of linear graphs”. In: Journal of the London Mathematical Society. 1. Jahrgang, Nr. 1, 1952, S. 127 (englisch).
- ↑ W. T. Tutte: The factors of graphs. In: Classic Papers in Combinatorics. 1987, S. 164–178 (englisch).
- ↑ a b T. Gallai: Neuer Beweis eines Tutte’schen Satzes, Magyar Tud. In: Akad. Kutató Int. Közl. 8. Jahrgang, 1963, S. 135–139.
- ↑ John H. Halton: A Combinatorial Proof of a Theorem of Tutte. In: Mathematical Proceedings of the Cambridge Philosophical Society. 62. Jahrgang, Nr. 04, 1966, S. 683–684, doi:10.1017/S0305004100040342 (englisch).
- ↑ M. L. Balinski: On perfect matchings. In: SIAM Review. 12. Jahrgang, 1970, S. 570–572 (englisch).
- ↑ I. Anderson: Perfect matchings of a graph. In: Journal of Combinatorial Theory, Series B. 10. Jahrgang, Nr. 3, 1971, S. 183–186 (englisch).
- ↑ W. Mader: 1-Faktoren von Graphen. In: Mathematische Annalen. 201. Jahrgang, Nr. 4, Dezember 1973, ISSN 0025-5831, S. 269–282, doi:10.1007/BF01428195.
- ↑ G. Hetyei: A new proof of a factorization theorem. In: Acta Acad. Paedagog. Civitate Pécs Ser. 6 Math. Phys. Chem. Tech. 16. Jahrgang, 1972, S. 3–6 (englisch).
- ↑ L. Lovasz: Three short proofs in graph theory. In: Journal of Combinatorial Theory, Series B. 19. Jahrgang, Nr. 3, 1975, S. 269–271 (englisch).
- ↑ Jungnickel 409.
- ↑ J. Edmonds: Paths, trees, and flowers. In: Canadian Journal of mathematics. 17. Jahrgang, Nr. 3, 1965, S. 449–467, doi:10.4153/CJM-1965-045-4 (englisch).
- ↑ Jungnickel 396.
- ↑ Betrachte dieses Beispiel nach Jungnickel 398.
- ↑ Diese Idee wurde in Oldenbourg U. Pape, D. Conradt: Ausgewählte Operations Research Software in FORTRAN. Oldenbourg 1979, ISBN 3-486-23911-2, Maximales Matching in Graphen, S. 103–114. vorgeschlagen. Jungnickel 399 hat ein Gegenbeispiel, das auf Christian Fremuth-Paeger zurückgeht.
- ↑ Harold N. Gabow: An Efficient Implementation of Edmonds’ Algorithm for Maximum Matching on Graphs. In: Journal of the ACM. 23. Jahrgang, Nr. 2, April 1976, ISSN 0004-5411, S. 221–234, doi:10.1145/321941.321942 (englisch).
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Beachte den Unterschied zwischen einem maximalen Element und einem Maximum. Bei der Formalisierung wird darauf genauer eingegangen.
- ↑ Es ist nicht bekannt, ob Petersen mit den Arbeiten von Euler 1736 zu diesem Problem vertraut war (Lovász & Plummer xi).
- ↑ notiert die symmetrische Differenz.
- ↑ Programmiersprachen, die das Konzept
Infnicht unterstützen, können die künstlichen Kanten stattdessen mit einer absurd großen Zahl belegen. genügt in jedem Fall.