Radiosity (Computergrafik)
Radiosity bzw. Radiosität ist ein Verfahren zur Berechnung der Verteilung von Wärme- oder Lichtstrahlung innerhalb eines virtuellen Modells. In der Bildsynthese ist Radiosity neben auf Raytracing basierenden Algorithmen eines der beiden wichtigen Verfahren zur Berechnung des Lichteinfalls innerhalb einer Szene. Es beruht auf dem Energieerhaltungssatz: Alles Licht, das auf eine Fläche fällt und von dieser nicht absorbiert wird, wird von ihr zurückgeworfen. Außerdem kann eine Fläche auch selbstleuchtend sein.
Das Radiosity-Verfahren basiert auf der Annahme, dass alle Oberflächen ideal diffuse Reflektoren bzw. alle Lichtquellen ideal diffuse Strahler sind. Ideal diffus bedeutet dabei, dass Licht in alle Richtungen gleichmäßig reflektiert bzw. abgestrahlt wird.
Im Gegensatz zu Raytracing ist Radiosity nicht vom Blickpunkt abhängig; die Beleuchtung der Flächen wird also für die gesamte Szene unabhängig von der Position des Betrachters berechnet. Die blickpunktabhängige Verdeckungsberechnung hat in einem unabhängigen Schritt zu erfolgen.
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Vorteile
[Bearbeiten | Quelltext bearbeiten]

- Blickpunktunabhängigkeit
- Ein Vorteil des Radiosity-Verfahrens ist, dass die Berechnung vom Standort und Blickwinkel des Betrachters unabhängig erfolgt. Die Lichtverteilung muss so für eine Szene nur einmal berechnet werden. Danach kann die Szene in Echtzeit gerendert werden (meist mittels Scanline-Algorithmen oder Z-Buffering), was für Anwendungen wie virtuelle Architekturmodelle interessant ist. Diesen Vorteil haben jedoch nicht alle Programme.
- Einfache indirekte, ideal diffuse Lichtreflexion
- Ideal diffuse Lichtreflexionen werden vom Radiosity-Verfahren auf natürliche Weise unterstützt. Die Helligkeit und Farbe einer Fläche werden nicht allein aufgrund der direkten Beleuchtung einer Lichtquelle, sondern auch durch diffus reflektiertes Licht anderer Flächen bestimmt. Ein Beispiel dafür ist ein Zimmer, das durch einfallendes Sonnenlicht nicht nur an den direkt beschienenen Stellen, sondern auch insgesamt heller wird.
Nachteile
[Bearbeiten | Quelltext bearbeiten]- Keine analytischen Primitiven
- Durch die zwingende Aufteilung der Szene in Polygone können keine analytisch definierten Primitiven, wie die bei Raytracing üblichen Kugeln, verwendet werden. Durch die zur Vermeidung von sichtbaren Kanten notwendige feine Aufteilung ist bei komplexer Szenengeometrie rasch eine sehr hohe Zahl von Flächen notwendig. Dies führt häufig zu einer hohen Wartezeit bei der Berechnung der Formfaktoren (siehe weiter unten).
- Es wurde versucht, mittels adaptativer Vereinfachung der Geometrie dieses Problem teilweise zu lösen,[1] was jedoch ein manueller Vorgang ist, der seine Grenzen hat. Daneben sind die aus den Fehlern dieses Verfahrens resultierenden Auswirkungen auf die Lichtberechnung schwer vorhersehbar.
- Hoher Speicher- und Zeitbedarf
- Wenn die Anzahl der Primitiven einer Szene ist, so weisen die effizientesten Radiosity-Varianten eine asymptotische Zeitkomplexität von auf, wie empirisch festgestellt wurde.[2] Dagegen benötigt Raytracing nur eine Laufzeit von . Dies begrenzt schnell den praktisch möglichen Verfeinerungsgrad bei Radiosity. Daneben ergeben sich zur Berechnung und Speicherung der Formfaktoren relativ hohe Speicheranforderungen.
- Globale Beleuchtung schwer realisierbar
- Für die möglichst realistische Darstellung einer Szene muss die globale Beleuchtung simuliert werden, was aber nur in Spezialfällen mit Radiosity effizient möglich ist. In seiner Grundform ist Radiosity nur zur Simulation ideal diffuser Reflexion fähig. Die Berücksichtigung beliebiger Beleuchtungsmodelle sowie transluzenter Flächen ist möglich,[3][4] hat jedoch keine breite Verwendung gefunden, da derartige Effekte schneller bzw. präziser mittels auf Raytracing basierter Lösungen möglich sind.
Vergleich mit Raytracing
[Bearbeiten | Quelltext bearbeiten]Historisch gesehen war Radiosity interessant, da es die Simulation indirekter diffuser Beleuchtung auf einfache Weise erlaubte, was mit Raytracing lange Zeit nicht möglich war. Andererseits war Raytracing gut für spiegelnde und transparente Objekte geeignet, wozu wiederum Radiosity nicht fähig war. Es wurden daher anfangs Vorschläge zur Kombination von Radiosity mit Raytracing gemacht, die jedoch aufwendig waren und sich letztendlich nicht im großen Maße durchsetzen konnten.
Mit dem Aufkommen moderner globaler Beleuchtungsverfahren wie Path Tracing und Photon Mapping wurden jedoch die Möglichkeiten von Raytracing beträchtlich erweitert. Weil derartige Algorithmen alle von Radiosity unterstützten Effekte mit weniger Fehlern und auf elegantere Weise simulieren können, ist Radiosity im Bereich der hochwertigen realistischen Bildsynthese weitgehend aus der Mode gekommen. Kommerzielle Verwendung findet Radiosity vor allem beim Rendern von Architekturmodellen, bei denen eine zeitaufwendige Vorausberechnung vertretbar ist. Auch derartige Anwendungen sind jedoch mit Raytracing-basierten Verfahren (Particle Tracing) möglich.[5]
Weitere Anwendung finden Radiosity-Verfahren in den Bereichen der Klima- bzw. Wärmeforschung, da Wärmeverteilung eher diffus als gerichtet geschieht und Radiosity hier praktikabler als strahlenbasierte Ansätze ist.
Prinzip
[Bearbeiten | Quelltext bearbeiten]Mit der eingangs formulierten Annahme kann die allgemeine Rendergleichung in die Radiosity-Gleichung überführt werden.
mit
- B(x) = gesamte vom Punkt x abgestrahlte Energie (Summe aus Eigenstrahlung und Reflexion als Leistung pro Flächeneinheit), genannt Radiosity im Punkt x
- E(x) = im Punkt x abgegebene Eigenstrahlung
- ρ(x) = Reflexionsfaktor im Punkt x
- S = alle Oberflächen der Szene
- r = Abstand der Punkte x und x'
- = Der Winkel zwischen der Normale im Punkt x und der Verbindungslinie zwischen den Punkten x und x'
- .
Die gesuchte Radiosity im Punkt x ergibt sich aus einem Integral in geschlossener Form, was auf direktem Weg nicht berechnet werden kann. Abhilfe schafft die Diskretisierung der Oberfläche S: anstatt alle infinitesimal kleinen Teilflächen δA' zu betrachten, teilt man die Oberfläche S in zusammenhängende Teilflächen (Facetten oder Patches genannt) Ai auf (Finite-Elemente-Methode). Für diese Teilflächen gelten weitere Annahmen: jedes Ai ist planar; die jeweilige Radiosity Bi und der Reflexionsfaktor ρi sind über Ai konstant. Dies führt dann zur diskreten Radiosity-Gleichung.
mit
- Bi = gesamte von Teilfläche i abgestrahlte Energie (Summe aus Eigenstrahlung und Reflexion als Leistung pro Flächeneinheit), genannt Radiosity der Teilfläche i
- Ei = von der Teilfläche i abgegebene Eigenstrahlung
- ρi = Reflexionsfaktor der Teilfläche i
- n = Anzahl der Teilflächen
- Fij = Anteil an der von Fläche j abgegebenen Energie, die auf Fläche i auftrifft, genannt Formfaktor.
Die Radiosity von Teilfläche ist also gleich der Eigenstrahlung der Teilfläche plus der mit dem diffusen Reflexionsfaktor gewichteten Summe der Radiosity von allen anderen Teilflächen . Wobei hierbei der Formfaktor , welcher den Anteil an der von Fläche j abgegebenen Energie die auf Fläche i auftrifft festlegt, eingeht. Der Formfaktor berücksichtigt also die Ausrichtung und den Abstand der Teilflächen zueinander. Da man dies für alle Teilflächen berechnen muss, ergibt sich ein lineares Gleichungssystem mit so vielen Gleichungen und Unbekannten wie es Teilflächen gibt.
1. Unterteilung der Oberflächen
[Bearbeiten | Quelltext bearbeiten]Im ersten Schritt erfolgt die Festlegung der Primitiven: Wie und in welche Teilflächen soll eine gegebene kontinuierliche Oberfläche zerlegt werden? Üblich sind Dreieck und Quadrat. Bereits in dieser Phase wird zwischen Qualität und Effizienz entschieden. Je feinmaschiger das Netz, desto genauer sind die Ergebnisse, aber umso aufwendiger die Berechnungen.
In der Praxis benutzt man meist adaptive Verfahren. Ausgehend von einer z. B. triangulierten Oberfläche, werden nach dem hier angegebenen Schema die zugehörigen Radiosity-Werte aller Facetten bestimmt. Mit diesen Daten erfolgen dann weitere ortsabhängige Netzverfeinerungen. Ausschlaggebend dafür können sein: ein hoher Radiosity-Gradient benachbarter Facetten, Diskontinuitäten im Lichtverlauf (z. B. Lichtfleck) oder eine örtlich ungünstige Netzeinteilung (z. B. T-Knoten).

2. Festlegung der Basisfunktionen
[Bearbeiten | Quelltext bearbeiten]Die diskrete Radiosity-Gleichung stellt eine Möglichkeit der Diskretisierung dar. Sie beruht auf der Annahme, dass die Radiosity über einer gegebenen Facette konstant ist, und verwendet daher konstante Basisfunktionen. Die Wahl von Basisfunktionen höheren Grads ist ebenfalls insbesondere mit dem Galerkin-Ansatz möglich.
3. Berechnung der Formfaktoren
[Bearbeiten | Quelltext bearbeiten]Der aufwendigste Schritt bei Radiosity ist, unabhängig von dem gewählten Algorithmus, die Berechnung der Formfaktoren. Ein Formfaktor gilt immer zwischen zwei Patches und beschreibt die Menge der ausgetauschten Strahlung, liegt also zwischen null (keine Strahlung wird ausgetauscht) und eins (alle Strahlung wird ausgetauscht).
Der Formfaktor ist rein geometrischer Natur und wird durch die Stellung der Patches zueinander bestimmt. Außerdem spielt die Sichtbarkeit der Patches eine Rolle. Die Sichtbarkeitsberechnung braucht bei weitem die meiste Zeit in der Berechnung.
Die Formel für einen Formfaktor lautet:
mit
- = Formfaktor zwischen dem Sender und dem Empfänger
- = Der Fläche des Senders
- = Der Fläche des Empfängers
- = Der Winkel zwischen der Normale des Senders und der Verbindungslinie zwischen Sender und Empfänger
- = Der Winkel zwischen der Normale des Empfängers und der Verbindungslinie zwischen Empfänger und Sender
- = Entfernung zwischen Sender und Empfänger
Da das direkte Berechnen dieses Doppelintegrals sehr schwierig ist, werden im Allgemeinen Annäherungen verwendet.
Das simpelste Verfahren ist nur für Flächen korrekt, die relativ klein und relativ weit entfernt sind und zwischen denen keine partielle Verdeckung besteht. Man berechnet dabei Winkel und Entfernung nur zwischen zwei repräsentativen Punkten, den Mittelpunkten der beiden Flächen.
Wobei der Mittelpunkt von und der Mittelpunkt von ist.
Methode nach Nusselt
[Bearbeiten | Quelltext bearbeiten]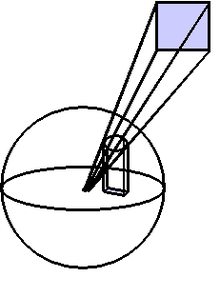
(auch „Nusselts Analogon“)
Es wird ein repräsentativer Punkt der Empfängerfläche, der Mittelpunkt, ausgewählt. Die sichtbaren Teile der Senderfläche werden auf die Einheitshalbkugel um diesen Punkt projiziert. Dadurch wird beachtet. Dann wird die Projektion auf der Einheitskugel wiederum in die Fläche, in der liegt, projiziert. Die entstandene Fläche wird durch geteilt (Fläche des Einheitskreises). Durch diesen Schritt wird der Formfaktor ermittelt.
Hemi-Cube-Verfahren
[Bearbeiten | Quelltext bearbeiten]
Von Cohen et al. stammt das sogenannte Hemi-Cube-Verfahren.[6] Die Einheitshalbkugel nach Nusselt wird durch einen Einheitshalbwürfel approximiert, dessen Seitenflächen in ein diskretes Gitter unterteilt sind. Jeder Gitterfläche wird ein Gewichtungsfaktor, der Delta-Formfaktor, zugeordnet, welcher von der Position der Gitterfläche abhängig ist. Ein Delta-Formfaktor ist damit der Formfaktor der Gitterfläche nach Nusselt. Die Summe der Delta-Formfaktoren ist 1.
Für jede der fünf Halbwürfelflächen wird mit modifizierten Rasteralgorithmen (üblicherweise Z-Buffer) ein Item-Buffer berechnet. Dieser enthält für jede Gitterfläche die Identität der Objektfläche (Item, rotes Dreieck im Bild), die darauf projiziert wurde. Für jedes Item wird die Summe der Delta-Formfaktoren der überdeckten Gitterflächen berechnet (rote Gitterflächen im Bild). Diese Summe wird als Formfaktor zwischen Item und betrachteter Fläche aufgefasst.
Sillions Verbesserung
[Bearbeiten | Quelltext bearbeiten]Statt eines Halbwürfels wird nun nur noch eine einzige Fläche verwendet, welche zentriert über dem differentiell kleinen Flächenstück (dA) platziert wird. Diese Fläche wird ebenfalls in kleine, diskrete Bereiche aufgeteilt. Diesen werden dann genau wie beim Hemicube-Verfahren in Abhängigkeit von der Geometrie zu dA, den sogenannten Delta-Formfaktoren zugeordnet. Der Vorteil bei diesem Verfahren ist, dass ein Patch nur auf diese eine Fläche projiziert werden muss und nicht mehr auf fünf Flächen eines Würfels. Außerdem ist dieses Verfahren legitim, da Patches, die orthogonal auf der Fläche von dA stehen, keinen großen Beitrag an der Gesamthelligkeit haben. Diese Beobachtung kann man sich über den Cosinus zwischen den Normalen der beiden Flächenstücke klarmachen.
4. Berechnung der Radiosity-Werte
[Bearbeiten | Quelltext bearbeiten]Die diskrete Radiosity-Gleichung kann als lineares Gleichungssystem aufgefasst werden und lässt sich demzufolge nach einigen Umformschritten wie folgt in Matrixform darstellen.
- oder kurz B = E+T•B.
Um alle gesuchten Radiosity-Werte zu bestimmen, muss das Gleichungssystem gelöst werden. Naheliegend ist die Invertierung der Matrix (I-T) (Matrix-Inversion nach Gauß), was aber aufgrund des enormen Aufwands unpraktikabel ist.
Im Allgemeinen existieren zwei unterschiedliche iterative Lösungsstrategien, die gegen die exakte Lösung konvergieren. Damit ist ein frei wählbarer Kompromiss zwischen Darstellungsqualität und Rechenzeit möglich.
- Beim Gathering wird die Radiosity Bi einer Facette durch Einsammeln aller einflussnehmenden Bj (abhängig vom jeweiligen Formfaktor) gebildet. Ausgangspunkt ist B0=E und man sieht nur die selbstleuchtenden Flächen. Nach dem ersten Schritt B1=E+T•B0 sind zusätzlich alle direkt beleuchteten Objekte sichtbar. Im nächsten Iterationsschritt B2=E+T•B1 werden die einfachen Reflexionen berücksichtigt usw. Auffällig ist, dass in jedem Schritt alle Formfaktoren benötigt werden. Auf diesem Prinzip beruhende Verfahren sind Jacobi-Iteration und Gauß-Seidel-Iteration.
- Beim Shooting wird die unverteilte Radiosity Bi auf alle als Empfänger in Frage kommenden Facetten (abhängig vom jeweiligen Formfaktor) geschossen. Ausgangspunkt sind wiederum die selbstleuchtenden Flächen, somit gilt B=E.
für jede Facette i
Radiosity B = Eigenleuchten E
unverteilte Radiosity ΔB = Eigenleuchten E
wiederhole
i = Facette mit maximaler Restenergie ΔBi•Ai
für jede Facette j
rad = ΔBi•ρj•Fji (wie viel der zu verteilenden Radiosity bekommt Facette j)
ΔBj = ΔBj+rad (zu verteilende Radiosity der Facette j wird um diesen Betrag erhöht)
Bj = Bj+rad (Radiosity der Facette j wird um diesen Betrag erhöht)
ΔBi = 0 (zu verteilende Radiosity der Facette i wurde verteilt und ist nun 0)
bis (Abbruchkriterium)
- Als Abbruchkriterien können neben objektiven Werten wie Fehlermetriken auch der subjektive Eindruck benutzt werden. Shooting-Verfahren sind den Gathering-Verfahren in zwei Gesichtspunkten überlegen. Zum einen kann aus dem Pseudocode abgeleitet werden, dass für jeden Iterationsschritt lediglich j Formfaktoren benötigt werden. Zum anderen wird in jedem Durchlauf die Radiosity der Facette mit der größten Restenergie verteilt, wodurch Shooting-Verfahren wesentlich schneller gegen „schöne“ Bilder konvergieren als Gathering-Verfahren. Auf diesem Prinzip beruhende Algorithmen sind Southwell-Iteration und Progressive-Refinement.
5. Rendern
[Bearbeiten | Quelltext bearbeiten]Den letzten Schritt bildet das Rendern des fertigen Bildes. Die an den ausgesuchten Stellen berechneten Radiosity-Werte werden gemäß den gewählten Basisfunktionen kombiniert. Wurden Radiosity-Werte in den Netzknoten bestimmt ist z. B. auch Gouraud Shading möglich. Genügt das so erstellte Bild dem Anspruch nicht, so können weitere Iterationen aus (4) folgen. Treten ungewollte grafische Artefakte auf, so sollte mit entsprechenden Änderungen in der Netzstruktur der Algorithmus von vorn gestartet werden.
Geschichtliche Entwicklung
[Bearbeiten | Quelltext bearbeiten]
1984 wurde das Verfahren erstmals von Goral et al.[7] vorgestellt. Es stammt aus der Thermodynamik, wo es verwendet wurde, um den Austausch von Wärmestrahlung zu berechnen (Strahlungsrechnung). Zu dieser Zeit wurde die Full-Form-Factor-Matrix-Methode zum Lösen des Gleichungssystems verwendet. Hier wird das Gleichungssystem für alle Formfaktoren zwischen allen Patches (=Flächen) der Welt aufgestellt und dann mittels eines mathematischen Verfahrens (meist dem Gauß-Seidel-Verfahren) gelöst. Prinzipiell entspricht dieses Vorgehen dem Einsammeln von Radiosity. Für jedes Patch wird berechnet, wie viel Licht es von jedem anderen Patch erhält. Das hat den Nachteil, dass die Berechnung der gesamten Matrix extrem viel Zeit benötigt und viel Speicherplatz belegt, was das Verfahren für komplexe Szenen unbrauchbar macht.
1988 wurde dann das Progressive-Refinement-Verfahren von Cohen et al. vorgestellt.[8] Hier wird der Prozess umgedreht, und das Licht wird nicht mehr an jedem Patch eingesammelt, sondern von jedem Patch verschossen. So kann man zuerst einmal das Licht von den Patches mit dem größten Radiositywert versenden und sich dann denen mit wenig Radiosity zuwenden. Hier ist es nicht mehr nötig, die gesamte Matrix zu berechnen, sondern es werden in jedem Schritt nur noch die Formfaktoren von einem einzelnen Patch zu allen anderen benötigt. Dadurch sinkt der benötigte Speicherplatz enorm, und man erhält nach jedem Schritt ein brauchbares Bild. Je länger man wartet, desto besser wird das Bild, da immer mehr Indirektionen berechnet werden. Um zu konvergieren, braucht dieses Verfahren allerdings genauso lange wie die Full-Form-Factor-Matrix-Methode.
Im Prinzip entspricht das Verfahren einer Reihenentwicklung der Matrix. Das Lineare Gleichungssystem, das sich aus der Strahlungsgleichung ergibt ist dann , wobei die Einheitsmatrix, die Matrix, bestehend aus den Formfaktoren und den Reflexionskoeffizienten und die Eigenstrahlung beschreibt. Stellt man die Gleichung nun um zu , so lässt sich der rechte Teil als Reihe der folgenden Form entwickeln, und man erhält eine inkrementelle Annäherung an die tatsächliche Strahlungsintensität:
- .
1991 wurde von Hanrahan et al. das Hierarchische Radiosity vorgestellt.[9] Bei diesem Verfahren wird eine Patchhierarchie verwendet. Wenige große Patches bestehen aus vielen kleinen. Der Lichtaustausch wird jetzt auf unterschiedlichen Stufen vorgenommen. Wenn der Fehler gering ist, wird das Licht auf einer hohen Hierarchieebene ausgetauscht, wenn ein großer Fehler zu erwarten ist (zum Beispiel wenn viel Licht ausgetauscht wird oder die Flächen sehr nahe beieinander liegen), dann wird das Licht auf einer niedrigeren Ebene ausgetauscht. Dadurch reduziert sich die Anzahl der zu berechnenden Formfaktoren substantiell, und die Berechnung wird deutlich beschleunigt.
Zusätzlich zu diesen Verfahren wurden noch viele Erweiterungen ersonnen. Zum Beispiel gibt es die Methode des Clustering[10], welches eine Erweiterung des Hierarchischen Radiosity ist. Hier wird oberhalb der Patchhierarchie eine weitere Hierarchie erzeugt, die Cluster. Licht kann dann auch zwischen ganzen Clustergruppen ausgetauscht werden, abhängig vom zu erwartenden Fehler. Wieder spart man sich die Berechnung vieler Formfaktoren.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Michael F. Cohen, John R. Wallace: Radiosity and Realistic Image Synthesis. Morgan Kaufmann, San Francisco 1993, ISBN 0-12-178270-0.
- François X. Sillion, Claude Puech: Radiosity and Global Illumination. Morgan Kaufmann, San Francisco 1994, ISBN 1-55860-277-1.
Quellen
[Bearbeiten | Quelltext bearbeiten]- ↑ H. E. Rushmeier u. A: Geometric simplification for indirect illumination calculations. In: Proceedings of Graphics Interface ’93. Canadian Information Processing Society, Toronto 1993, S. 227–236 (smartech.gatech.edu ( vom 7. August 2016 im Webarchiv archive.today) PDF).
- ↑ M. F. Cohen u. A.: Radiosity and realistic image synthesis. Academic Press Professional, San Diego 1993, ISBN 0-12-178270-0.
- ↑ H. Rushmeier, K. Torrance: Extending the radiosity method to include specularly reflecting and translucent materials. In: ACM Transactions on Graphics. Band 9, S. 1–27, ACM Press, New York 1990 (graphics.cornell.edu PDF)
- ↑ E. Gobbetti u. A.: Hierarchical Higher Order Face Cluster Radiosity for Global Illumination Walkthroughs of Complex Non-Diffuse Environments. In: Computer Graphics Forum, Band 22-3 (9/2003).
- ↑ B. Walter u. A.: Global Illumination Using Local Linear Density Estimation. In: ACM Transactions on Graphics, Vol. 16-3 (7/1997), S. 217–259, ACM Press, New York 1997
- ↑ M. F. Cohen, D. P. Greenberg: The hemi-cube: a radiosity solution for complex environments. In: Proceedings of the 12th annual conference on Computer graphics and interactive techniques, S. 31–40, ACM Press, New York 1985, ISBN 0-89791-166-0
- ↑ C. Goral, K. E. Torrance, D. P. Greenberg und B. Battaile: Modeling the interaction of light between diffuse surfaces. (PDF; 1,1 MB) In: Computer Graphics. Band 18, Nr. 3.
- ↑ M. F. Cohen u. A.: A progressive refinement approach to fast radiosity image generation. In: Proceedings of the 15th annual conference on Computer graphics and interactive techniques, S. 75–84, ACM Press, New York 1988
- ↑ Pat Hanrahan u. A.: A Rapid Hierarchical Radiosity Algorithm. In: Proceedings of the 18th annual conference on Computer graphics and interactive techniques, S. 197–206, ACM Press, New York 1991
- ↑ B. Smits u. A.: A Clustering Algorithm for Radiosity in Complex Environments. In: Proceedings of the 21st annual conference on Computer graphics and interactive techniques. ACM Press, New York 1994, S. 435–442 (cs.ucl.ac.uk ( vom 10. März 2004 im Internet Archive) PDF)






































