Sierpinski-Dreieck

Sierpinski-Dreieck mit Rekursionstiefe 7

Das Sierpinski-Dreieck ist ein 1915 von Wacław Sierpiński beschriebenes Fraktal – mitunter auch Sierpinski-Fläche oder -Dichtung genannt, welches eine selbstähnliche Teilmenge eines (meist gleichseitig dargestellten) Dreiecks ist. Teilt man das Dreieck in vier zueinander kongruente und zum Ausgangsdreieck ähnliche Dreiecke, deren Eckpunkte die Seitenmittelpunkte des Ausgangsdreiecks sind, dann sind die Teilmengen des Fraktals in den drei äußeren Dreiecken skalierte Kopien des gesamten Fraktals, während das mittlere Teildreieck nicht zum Fraktal gehört. Diese Aufteilung des Fraktals in skalierte Kopien kann in den äußeren Teildreiecken rekursiv fortgesetzt werden. Die fraktale Dimension des Sierpinski-Dreiecks beträgt

$D=\log _{2}3\approx 1{,}58496\ldots$

Konstruktion

Algorithmus

Zur Darstellung des Sierpinski-Dreiecks wird als Ausgangsdreieck meist ein gleichseitiges Dreieck gewählt; das ist nicht zwingend, aus jedem Dreieck kann ein Sierpinski-Dreieck erzeugt werden.

Schrittweise Konstruktion des Sierpinski-Dreiecks

Der „klassische“ Algorithmus, der zur grafischen Demonstration des Fraktalbegriffs verwendet wird, ist folgender:

1. Zeichne ein Dreieck („Initiator“)
2. Verbinde die Mittelpunkte der Seiten („Generator“) (dadurch wird das ursprüngliche Dreieck in vier deckungsgleiche Teildreiecke zerlegt)
3. Entferne das mittlere der vier Teildreiecke (die anderen drei Teildreiecke bleiben übrig)
4. Wende Schritte 2 und 3 auf die drei übriggebliebenen Teildreiecke an usw.

Dieser Algorithmus verdeutlicht den Zusammenhang. Es entstehen bei jedem Iterationsschritt an den Ecken drei (zum Initiator ähnliche) Dreiecke mit halber Seitenlänge und einem Viertel der Fläche, die gefärbt werden. Das vierte „innere“ kleine Dreieck, welches dabei entsteht, kann man sich als aus der Dreiecksfläche des vorhergehenden Schritts „herausgeschnitten“ vorstellen.

Das eigentliche Sierpinski-Dreieck im streng mathematischen Sinn ist das Grenzobjekt, das nach unendlich vielen Iterationsschritten übrigbleibt. Es besteht aus unendlich vielen „Eckpunkten“. Zur Darstellung, die meist mit rekursiven Computerprogrammen realisiert und nach Bedarf auf einem Bildschirm angezeigt oder ausgedruckt wird, reicht meist schon eine Iterations- oder Rekursionstiefe von höchstens zehn. Bedingt durch die Auflösung des darstellenden Mediums (Monitor, Drucker etc.) und des menschlichen Auges sind diese Gebilde vom Grenzobjekt nicht mehr zu unterscheiden. In klassischer planimetrischer Flächenmessung geht die Fläche mit zunehmender Iterationstiefe gegen Null.

Lindenmayer-System

Das Sierpinski-Dreieck lässt sich durch ein Lindenmayer-System mit folgenden Eigenschaften beschreiben:

• Winkel: 120°
• Startstring: $A+A+B$
• Ableitungsregeln:
  • $A\mapsto AA$
  • $B\mapsto B+A-B-A+B$

Darstellung in Wolframs eindimensionalen Universum

In Stephen Wolframs eindimensionalen zellulären Automaten erzeugt eine einzelne lebende Zelle in Regel 90 ein Sierpinski-Dreieck.

Mathematische Zusammenhänge

Das Sierpinski-Dreieck ist selbstähnlich

Als klassisches Fraktal ist das Sierpinski-Dreieck ein Musterbeispiel für exakte Selbstähnlichkeit: Die in jedem Schritt erzeugten äußeren Teildreiecke enthalten verkleinerte exakte Kopien des gesamten Fraktals. Eine passende Skalierung eines beliebigen dreieckigen Teils des Fraktals erscheint wie das Gesamtobjekt selbst. Es ist somit skaleninvariant.

Von den zugrundeliegenden mathematischen Gesetzmäßigkeiten her ist das Sierpinski-Dreieck eng verwandt mit der Cantor-Menge. Seine Dimension ist der Kehrwert derselben, nämlich $\log(3)/\log(2)=1{,}585$. Dies resultiert daraus, dass bei jedem Schritt $k$ genau $3^{k}$ neue Teildreiecke mit der Seitenlänge $(1/2)^{k}$ erzeugt werden. Das Fraktal entsteht als Grenzobjekt, wenn $k$ gegen unendlich geht, genauer indem der Durchschnitt aller Zwischenschritte der Konstruktion gebildet wird und es kann daher als „geometrisches Analogon“ zu einem Grenzwert aufgefasst werden. Aus der Bildungsvorschrift lässt sich auch berechnen, welche Punkte der ursprünglichen Fläche zum Grenzobjekt gehören.

Zur Berechnung der Anzahl der Dreiecke nach k Iterationen lässt sich folgende Formel anwenden:

$N=2\cdot 3^{k}-1$ für $k\in \mathbb {N}$

Darstellung mittels Hutchinson-Operator

Ein Sierpinski-Dreieck lässt sich auch als Attraktor eines dynamischen Rückkopplungsprozesses, eines deterministisch iterierten Funktionensystems mit geeigneten Parametern aus nahezu jeder beliebigen geometrischen Figur darstellen. Dabei werden wiederholt Mehrfach-Transformationen des Ausgangsobjektes vorgenommen, diese Bilder mit einer Abbildungsvorschrift, dem Hutchinson-Operator, entsprechend angeordnet und diese Prozedur erneut auf das entstandene Gesamtbild angewandt usw. Mit zunehmender Iterationstiefe streben die entstehenden Bilder, falls geeignete Parameter gewählt wurden, einem Sierpinski-Dreieck zu, das in diesem Falle der Attraktor des Funktionensystems ist.

Das Sierpinski-Dreieck ist in diesem Sinne charakterisiert als diejenige kompakte Teilmenge der Ebene, die identisch ist mit der Vereinigung ihrer drei Bilder unter den drei Ähnlichkeitsabbildungen, die das gesamte Dreieck jeweils auf die drei halb so großen Teildreiecke abbilden.

Stufe	1	2	3	4	5	6	7	8

Sierpinski-Tetraeder

Ein Sierpinski-Tetraeder

Eine Darstellung des Sierpinksi-Dreiecks ist, analog zum Menger-Schwamm, auch in der dritten Dimension möglich: Die Startfigur ist ein Tetraeder. Aus dessen Mitte wird in jedem Iterationsschritt ein Oktaeder mit halber Kantenlänge herausgeschnitten. Übrig bleiben vier Tetraeder, aus denen wieder je ein Oktaeder herausgeschnitten wird, usw. Die Dimension für dieses Gebilde ist $D={\frac {\log(4)}{\log(2)}}=2$, obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das Volumen der Figur gegen 0; die Oberfläche bleibt jedoch konstant.

Chaos-Spiel

Abgesehen von der rekursiven Darstellung gibt es noch einen Zufallspunkt-Algorithmus zur näherungsweisen Konstruktion des Sierpinski-Dreiecks: Das Chaos-Spiel.

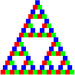
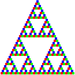
Dabei wird ein gleichseitiges Dreieck mit den Ecken A, B, C aufgezeichnet und ein zufälliger Punkt im Inneren des Dreiecks gewählt (er kann aber auch außerhalb liegen, ohne das Ergebnis wesentlich zu verändern). Nun wird pro Schritt eine Ecke zufällig ausgewählt (die Wahrscheinlichkeiten für die Ecken sind jeweils gleich) und der Punkt gedanklich mit der gezogenen Ecke verbunden. Die Mitte dieser Strecke markiert nun den Punkt für die nächste Runde. Wiederholt man dies sehr oft, bilden die Punkte eine Näherung des Sierpinski-Dreiecks. Wenn man die Punkte auch noch je nach ausgewählter Ecke unterschiedlich einfärbt, also z. B. A = grün, B = rot und C = blau, dann bekommt man drei unterschiedlich gefärbte Sierpinski-Dreiecke im Sierpinski-Dreieck.

Man kann aus der iterativen Struktur des Sierpinski-Dreiecks beweisen, dass ein mittels dieses Algorithmus gewonnener Punkt genau dann zum Sierpinski-Dreieck gehört, wenn auch der Ausgangspunkt Teil des Sierpinski-Dreiecks ist. Wenn man also beispielsweise einen Punkt der Strecke AB als Ausgangspunkt wählt, hat man nach unendlich vielen Iterationen ein Sierpinski-Dreieck konstruiert.

Zusammenhang mit dem Pascalschen Dreieck

Mit dem Sierpinski-Dreieck verwandt ist das Pascalsche Dreieck. Dabei entsprechen die geraden Zahlen im Pascal-Dreieck den Lücken im Sierpinski-Dreieck. Beide Dreiecke haben eine einfache Iterationsvorschrift, aus der stets eine geometrische Ähnlichkeit hervorgeht: Wird in einem Schritt beim Sierpinski-Dreieck jedes Initiatordreieck nach oben bereits beschriebener Regel ersetzt, so wird beim Pascal-Dreieck lediglich die Anzahl der Zeilen verdoppelt (ungerade Zahlen mit mehr als einer Dezimalstelle werden im Folgenden der übersichtlicheren Darstellung halber als # dargestellt).

Initiator:

           1
          1 1

1. Schritt

           1
          1 1
         1   1
        1 3 3 1

2. Schritt

           1
          1 1
         1   1
        1 3 3 1
       1       1
      1 5     5 1
     1   #   #   1
    1 7 # # # # 7 1

3. ...

Diese Ähnlichkeit ist sowohl für ein unendliches Pascal-Dreieck als auch ein Sierpinski-Dreieck nach unendlich vielen Iterationsschritten gegeben.

Das Erzeugen dieser Ähnlichkeit kann auch aus einer anderen Sichtweise betrachten werden: Das Pascal-Dreieck selbst ist als Idee und damit als geometrischer Bauplan immer unendlich, wir können es nur nicht komplett aufschreiben. Ein iterativ erzeugtes Sierpinski-Dreieck aber ist stets durch seine äußere Hülle beschränkt. Somit wird durch fortlaufende Iteration nicht das Pascal-Dreieck an ein Sierpinski-Dreieck, sondern das Sierpinski-Dreieck an den unendlichen geometrischen Bauplan und damit an das unendliche Pascal-Dreieck angeglichen.

Natur

In der Natur kommt dieses Muster auf dem Gehäuse der Schneckenart Cymbiola innexa vor.

Siehe auch

• Sierpinski-Kurve
• Sierpinski-Teppich
• Fraktalantenne
• Türme von Hanoi
• Tetraeder (Bottrop)
• Triforce

Weblinks

Commons: Sierpinski-Dreieck – Album mit Bildern, Videos und Audiodateien

• Eric W. Weisstein: Sierpiński Sieve. In: MathWorld (englisch).
• Java-Applet zur Demonstration des Dreiecks
• Interaktive Konstruktion zum Ausprobieren mit JSXGraph
• Erklärung und Java-Applet zum Chaos-Spiel
  • Implementierung in .NET
• Sierpinski-Dreieck mit MS Excel erstellen
• Sierpinski-Dreieck mit HTML5-Canvas und JavaScript