Pascalsches Dreieck
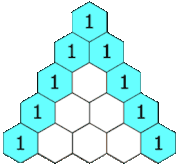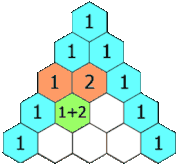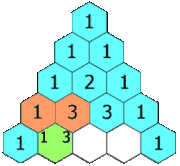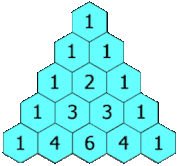
Das Pascalsche (oder Pascal’sche) Dreieck ist eine Form der grafischen Darstellung der Binomialkoeffizienten , die auch eine einfache Berechnung dieser erlaubt. Sie sind im Dreieck derart angeordnet, dass jeder Eintrag die Summe der zwei darüberstehenden Einträge ist. Dieser Sachverhalt wird durch die Gleichung
beschrieben. Dabei kann die Variable als Zeilenindex und als Spaltenindex interpretiert werden, wobei die Zählung mit Null beginnt (also erste Zeile , erste Spalte ). Beginnt man an den Rändern mit Einträgen mit dem Wert , so ergeben sich dadurch genau die Binomialkoeffizienten.
Der Name geht auf Blaise Pascal zurück. Das pascalsche Dreieck war jedoch schon früher bekannt und wird deshalb auch heute noch nach anderen Mathematikern benannt. In China spricht man vom Yang-Hui-Dreieck (nach Yang Hui), in Italien vom Tartaglia-Dreieck (nach Nicolo Tartaglia) und im Iran vom Chayyām-Dreieck (nach Omar Chayyām).
Geschichte[Bearbeiten | Quelltext bearbeiten]


Die früheste detaillierte Darstellung eines Dreiecks von Binomialkoeffizienten erschien im 10. Jahrhundert in Kommentaren zur Chandas Shastra, einem indischen Buch zur Prosodie des Sanskrit, das von Pingala zwischen dem fünften und zweiten Jahrhundert vor Christus geschrieben wurde. Während Pingalas Werk nur in Fragmenten erhalten blieb, verwendete der Kommentator Halayudha um 975 das Dreieck, um zweifelhafte Beziehungen zu Meru-prastaara den „Stufen des Berges Meru“ herzustellen. Es war auch schon bekannt, dass die Summe der flachen Diagonalen des Dreiecks die Fibonaccizahlen ergeben. Vom indischen Mathematiker Bhattotpala (ca. 1070) sind die ersten 17 Zeilen des Dreiecks überliefert.
Annähernd zur gleichen Zeit wurde das pascalsche Dreieck im Nahen Osten von al-Karadschi (953–1029), as-Samaw'al und Omar Chayyām behandelt und ist deshalb im heutigen Iran als Chayyām-Dreieck bekannt. Es waren verschiedene mathematische Sätze zum Dreieck bekannt, unter anderem der binomische Lehrsatz. Tatsächlich ist es ziemlich sicher, dass Chayyām ein Verfahren zur Berechnung der -ten Wurzel verwendet hat, das auf der binomischen Erweiterung und damit den Binomialkoeffizienten beruht.
Die früheste chinesische Darstellung eines mit dem pascalschen Dreieck identischen arithmetischen Dreiecks findet sich in Yang Huis Buch Xiangjie Jiuzhang Suanfa von 1261, das ausschnittsweise in der Yongle-Enzyklopädie erhalten geblieben ist.[1] Yang schreibt darin, das Dreieck von Jia Xian (um 1050) und dessen li cheng shi shuo („Ermittlung von Koeffizienten mittels Diagramm“) genannter Methode zur Berechnung von Quadrat- und Kubikwurzeln übernommen zu haben.[2][3]
Peter Apian veröffentlichte das Dreieck 1531/32 auf dem Titelbild seines Buchs über Handelsberechnungen, dessen frühere Version von 1527 den ersten schriftlichen Nachweis des pascalschen Dreiecks in Europa darstellt.
1654 schrieb Blaise Pascal sein 1665 veröffentlichtes Buch Traité du triangle arithmétique (Abhandlung über das arithmetische Dreieck), in dem er verschiedene Ergebnisse bezüglich des Dreiecks sammelte und diese dazu verwendete, Probleme der Wahrscheinlichkeitstheorie zu lösen. Das Dreieck wurde später von Pierre Rémond de Montmort (1708) und Abraham de Moivre (1730) nach Pascal benannt.[4]
Anwendung[Bearbeiten | Quelltext bearbeiten]
Das Pascalsche Dreieck gibt eine Handhabe, schnell beliebige Potenzen von Binomen auszumultiplizieren. So befinden sich in der zweiten Zeile () die Koeffizienten 1, 2, 1 der ersten beiden Binomischen Formeln:
In der nächsten, der dritten Zeile finden sich die Koeffizienten 1, 3, 3, 1 für :
Diese Auflistung kann beliebig fortgesetzt werden, wobei zu beachten ist, dass für das Binom stets das Minuszeichen aus „“ zu nehmen ist und dass, während der Exponent von in jeder Formel stets um 1 abnimmt, der Exponent von um 1 zunimmt. Eine Verallgemeinerung liefert der Binomische Lehrsatz.
Des Weiteren wechseln sich bei der Anwendung des Pascalschen Dreieck auf das Binom mit einem beliebigen Exponenten die Vorzeichen – und + ab (es steht immer dann ein Minus, wenn der Exponent von ungerade ist). Das heißt z. B.
Eine zweidimensionale Verallgemeinerung ist das Trinomial Triangle, in welchem jede Zahl die Summe von drei (statt im Pascalschen Dreieck: von zwei) Einträgen ist. Eine Erweiterung in die dritte Dimension ist die Pascalsche Pyramide.
Folgen im Pascalschen Dreieck[Bearbeiten | Quelltext bearbeiten]
Im Pascalschen Dreieck finden sich viele bekannte Zahlenfolgen wieder.
Die Diagonalen[Bearbeiten | Quelltext bearbeiten]
Die erste Diagonale enthält nur Einsen und die zweite Diagonale die Folge der natürlichen Zahlen. In der dritten Diagonale finden sich die Dreieckszahlen und in der vierten die Tetraederzahlen. Allgemein findet man in der -ten Diagonale die regulären figurierten Zahlen der Ordnung . In jeder Diagonale steht die Folge der Partialsummen zu der Folge, die in der Diagonale darüber steht. Umgekehrt ist jede Diagonalenfolge die Differenzenfolge zu der in der Diagonale unterhalb stehenden Folge.
Allgemein gilt also für die Dreieckszahlen
- ,
für die Tetraederzahlen
und für die regulären figurierten Zahlen der Ordnung
- .
Die Fibonacci-Zahlen[Bearbeiten | Quelltext bearbeiten]

Die Summen der hier grün, rot und blau markierten flachen „Diagonalen“ ergeben jeweils eine Fibonacci-Zahl (1, 1, 2, 3, 5, 8, 13, 21, 34, …). In diesem Beispiel ist die Summe der grünen Diagonale gleich 13, die Summe der roten Diagonale gleich 21, die Summe der blauen Diagonale gleich 34. Dass sich die „Diagonale“ manchmal nicht von einem zum anderen Ende „durchziehen“ lässt, wie im Fall der roten Diagonale, ist unerheblich.
Allgemein gilt also
Die Zeilen[Bearbeiten | Quelltext bearbeiten]
Die Summe der Einträge einer Zeile wird als Zeilensumme bezeichnet. Von oben nach unten verdoppeln sich die Zeilensummen von Zeile zu Zeile. Dies rührt vom Bildungsgesetz des pascalschen Dreiecks her. Jeder Eintrag einer Zeile wird in der folgenden Zeile zur Berechnung zweier Einträge verwendet. Hierbei muss man das Bildungsgesetz durch das Hinzufügen von gedachten Nullen links und rechts von jeder Zeile verallgemeinern, so dass auch die äußeren Einsen jeder Zeile durch die Addition der darüberliegenden Einträge generiert werden. Da die Zeilensumme der ersten Zeile gleich eins ist, ist die Zeilensumme der -ten Zeile gleich . Dies entspricht dem folgenden Gesetz für Binomialkoeffizienten:
Reiht man jeweils die Ziffern der ersten fünf Zeilen des pascalschen Dreiecks aneinander, erhält man mit 1, 11, 121, 1331 und 14641 die ersten Potenzen von 11.
Die alternierende Summe jeder Zeile ergibt Null: , .
Formal folgen die drei obigen Formeln aus dem binomischen Lehrsatz für , und .
Mittlere Binomialkoeffizienten[Bearbeiten | Quelltext bearbeiten]
Die Folge der mittleren Binomialkoeffizienten beginnt mit 1, 2, 6, 20, 70, 252, … (Folge A000984 in OEIS).
Zusammenhang mit dem Sierpinski-Dreieck[Bearbeiten | Quelltext bearbeiten]
Das Pascalsche Dreieck ist mit dem Sierpinski-Dreieck, das 1915 nach dem polnischen Mathematiker Wacław Sierpiński benannt wurde, verwandt. Beide Dreiecke verwenden eine einfache, aber leicht unterschiedliche Iterationsvorschrift, die eine geometrische Ähnlichkeit hervorbringt.
Potenzen mit beliebiger Basis[Bearbeiten | Quelltext bearbeiten]
Für Potenzen mit beliebiger Basis existiert ein Zahlendreieck anderer Art:
Zu dieser Dreiecksmatrix gelangt man durch Inversion der Matrix der Koeffizienten derjenigen Terme, die die Kombinationen ohne Wiederholung der Form für usw. darstellen.
- Beispiel
- .
- Lesart
- Beispiel
Das Bildungsgesetz der Koeffizienten für den Koeffizienten in Zeile und Spalte lautet:
es gilt daher auch mit der Stirling-Zahl .
Mit Hilfe dieses Dreiecks gewinnt man unmittelbare Einblicke in die Teilbarkeit von Potenzen. So ist jede Primzahlpotenz für kongruent modulo . Dies ist im Wesentlichen der Inhalt des kleinen Fermatschen Satzes; zusätzlich wird jedoch gezeigt, dass der Ausdruck für alle nicht nur durch , sondern für auch durch 6 teilbar ist. Der größte gemeinsame Teiler der Matrixkoeffizienten ab dem zweiten Koeffizienten der Primzahlexponenten für entspricht stets dem Nenner der jeweiligen bernoullischen Zahl (Beispiel: : Nenner = 6; : Nenner = 30 usw.)
Mit diesem Zahlendreieck kann beispielsweise mühelos bewiesen werden, dass durch 24 teilbar ist:
- (mit , , usf.)
ist stets durch 24 teilbar, da wegen auch sind.
Zusammenhang mit dem Wallisschen Produkt[Bearbeiten | Quelltext bearbeiten]
John Wallis nutzte 1655 eine schachbrettartige Interpolation zwischen den (je Dimension) figurierten Zahlenfolgen zur erstmaligen Berechnung einer Darstellung von 4/ als unendliches Produkt.[5]
Sonstiges[Bearbeiten | Quelltext bearbeiten]
- Über die Anzahlen, mit der eine Zahl im Pascalschen Dreieck vorkommt, gibt es die Singmaster-Vermutung.
- Summiert man die ersten vier Terme jeder Reihe des Pascalschen Dreiecks, so erhält man die Kuchenzahlen.[6]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- John H. Conway, Richard K. Guy: Zahlenzauber. Von natürlichen, imaginären und anderen Zahlen. Birkhäuser Verlag, Basel 1997, ISBN 3-7643-5244-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Ho Peng Yoke: Li, Qi and Shu. An Introduction to Science and Civilization in China. Hongkong University Press, 1985, ISBN 0-486-41445-0, S. 97 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ George Gheverghese Joseph: The Crest of the Peacock. Non-European Roots of Mathematics. 3. Auflage. Princeton University Press, 2011, ISBN 978-0-691-13526-7, S. 247 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Duan Yao-Yung, Kostas Nikolantonakis: The Algorithm of Extraction in Greek and Sino-Indian Mathematical Traditions. In: B.S. Yadav, Man Mohan (Hrsg.): Ancient Indian Leaps into Mathematics. Birkhäuser, 2011, ISBN 978-0-8176-4695-0, S. 180–181, doi:10.1007/978-0-8176-4695-0_11.
- ↑ Jeff Miller: Pacal's Triangle. In: Earliest Known Uses of Some of the Words of Mathematics. University of St Andrews, abgerufen am 19. Dezember 2023 (englisch).
- ↑ alphagalileo.org (Memento vom 22. November 2015 im Internet Archive)
- ↑ COMMENTS der Folge A000125 in OEIS






















































































![{\displaystyle E(i,j)=[E(i-1,j-1)+E(i-1,j)]\cdot j}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b9cad5210a10bdfd206c20db903ebdc3ac721ae)
















