Surreale Zahl
Die surrealen Zahlen bilden eine Klasse von Zahlen, die alle reellen Zahlen umfasst, sowie „unendlich große“ Zahlen, die größer sind als jede reelle Zahl. Dabei ist jede reelle Zahl von surrealen Zahlen umgeben, die ihr näher sind als jede andere reelle Zahl, insbesondere gibt es „infinitesimale“ Zahlen, die näher bei Null liegen als jede positive reelle Zahl. Darin stimmen sie mit den hyperreellen Zahlen überein, aber sie werden auf eine substanziell andere Weise konstruiert und enthalten die hyperreellen Zahlen als Teilmenge.
Das Wort „surreal“ entstammt dem Französischen und bedeutet „über der Wirklichkeit“. Es wird auch für die Stilrichtung des Surrealismus verwendet.
Surreale Zahlen wurden zuerst von John Conway vorgestellt und 1974 im Detail beschrieben in Donald E. Knuths mathematischem Roman Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. In seinem Buch, das in Dialogform gehalten ist, prägte Knuth den Begriff surreale Zahlen für das, was Conway ursprünglich nur Zahlen nannte. Conway gefiel der neue Name, sodass er ihn später übernahm. Er beschrieb die surrealen Zahlen und nutzte sie zur Analyse von Spielen (unter anderem Go) in seinem Mathematikbuch On Numbers and Games (1976).
Motivation[Bearbeiten | Quelltext bearbeiten]
Surreale Zahlen sind aus mehreren Gründen interessante Strukturen: Zum einen entstehen sie durch zwei einfache Regeln „aus dem Nichts“ und haben trotzdem ähnliche Eigenschaften wie die reellen Zahlen. Wir sind gezwungen, jede Aussage zu beweisen, die wir bei den reellen Zahlen für selbstverständlich erachten, z. B. dass gilt oder dass aus stets folgt. Die surrealen Zahlen sind daher eine gute Möglichkeit, Methoden der abstrakten Algebra zu üben. Von Conway wurden einige Anwendungen in der Spieltheorie präsentiert (siehe unten den Abschnitt zur Spieltheorie). Schließlich bilden die surrealen Zahlen wie die hyperreellen Zahlen ein Modell der Nichtstandardanalysis, in der z. B. infinitesimale Zahlen existieren.
Bevor wir beginnen, surreale Zahlen zu definieren, sollten wir uns klarmachen, dass wir mit der Konstruktion der surrealen Zahlen rein mengentheoretisch beginnen und über Zahleneigenschaften wie „kleiner“, Null, Eins, Addition und Multiplikation zunächst nichts wissen.
Konstruktion[Bearbeiten | Quelltext bearbeiten]
Die Grundidee hinter der Konstruktion der surrealen Zahlen ist ähnlich den Dedekind-Schnitten. Wir erzeugen eine neue Zahl, indem wir zwei Mengen und von Zahlen angeben, die die neue Zahl annähern. Die Menge besteht aus Zahlen, die kleiner sind als die neue Zahl, und ist eine Menge von Zahlen, die größer sind als die neue Zahl. Wir schreiben eine solche Darstellung als . An die Mengen und stellen wir nur die Bedingung, dass jedes Element von kleiner sein soll als jedes Element von . Zum Beispiel ist eine gültige („wohlgeformte“) Konstruktion einer bestimmten Zahl zwischen und . (Welche das ist, wird später erklärt.) Es ist ausdrücklich erlaubt, dass die Mengen leer sind. Die Interpretation der Darstellung ist „eine Zahl, die größer ist als jede Zahl in “, und ist „eine Zahl, die kleiner ist als jede Zahl in “. Das Konstruktionsprinzip der surrealen Zahlen ist allerdings hochrekursiv; neben einer Konstruktionsregel brauchen wir auch eine Vergleichsregel für die rekursiv erklärte Ordnungsrelation (kleinergleich), die für die Anwendung der Konstruktionsregel benutzt werden muss.
Konstruktions- und Vergleichsregel[Bearbeiten | Quelltext bearbeiten]
- Konstruktionsregel
- Sind und zwei Mengen von surrealen Zahlen und kein Element von ist kleiner oder gleich einem Element von , dann ist eine surreale Zahl. Jede surreale Zahl lässt sich auf diese Art beschreiben.
Ist eine surreale Zahl gegeben, dann nennen wir die linke Menge und die rechte Menge von .
- Vergleichsregel
- Für zwei surreale Zahlen und gilt , falls kleinergleich keinem Element von ist und kein Element von kleinergleich ist.
Zur Vereinfachung der Notation lassen wir die Mengenklammern und die leere Menge bei linker und rechter Menge weg, wo keine Missverständnisse zu befürchten sind, d. h. wir schreiben z. B. für bzw. für . Ein Objekt , das die Kleiner-Gleich-Bedingung erfüllt, nennt man auch wohlgeformt, um es von später betrachteten Objekten ohne diese Bedingung zu unterscheiden (den sogenannten Games).
Diese beiden Regeln sind rekursiv, also brauchen wir eine Form von Induktion, um mit ihnen zu arbeiten. Ein Kandidat wäre die vollständige Induktion, aber wie wir später sehen werden, macht erst die transfinite Induktion die Sache richtig interessant, d. h., wenn man diese Regeln „mehr als endlich oft“ anwendet.
Relationen[Bearbeiten | Quelltext bearbeiten]
Damit die erzeugten Objekte sinnvollerweise Zahlen genannt werden können, sollten sie eine totale Ordnung haben. Die Relation ist jedoch nur eine totale Quasiordnung, d. h. sie ist reflexiv und transitiv, aber nicht antisymmetrisch (aus und folgt nicht notwendig, dass ). Um dem abzuhelfen, definieren wir eine Relation auf den surrealen Zahlen:
- Es gelte genau dann, wenn und
Dies ist eine Äquivalenzrelation, und die Äquivalenzklassen sind total geordnet. Liegen und in derselben Äquivalenzklasse, dann stellen sie dieselbe surreale Zahl dar. Die Äquivalenzklasse von schreiben wir als , wobei ein Repräsentant der Klasse ist. Es ist also gleichwertig zu . Dieses Vorgehen entspricht der Konstruktion der rationalen Zahlen als Äquivalenzklassen von Brüchen ganzer Zahlen, der Konstruktion der reellen Zahlen als Äquivalenzklassen von Cauchy-Folgen oder der Konstruktion der hyperreellen Zahlen als Äquivalenzklassen von reellen Folgen.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Betrachten wir nun einige Beispiele von surrealen Zahlen. Da wir noch keine surrealen Zahlen kennen, ist die einzige Menge, die wir für und nehmen können, die leere Menge. Unsere erste Zahl ist also
Diese Zahl erfüllt die Konstruktionsregel, da die leere Menge kein Element enthält, das irgendeine Bedingung verletzen könnte. Wir nennen sie und ihre Äquivalenzklasse schreiben wir als . Nach der Vergleichsregel gilt
- .
Durch Anwendung der Konstruktionsregel erhalten wir die Zahlen
- und
Die letzte Zahl ist jedoch wegen keine wohlgeformte surreale Zahl. Die bisher gefundenen Zahlen lassen sich so ordnen:
Dabei bedeutet , dass nicht gilt. Wir nennen die neuen Zahlen und und ihre Äquivalenzklassen und . Da die Äquivalenzklassen bisher nur je ein Element enthalten, können wir diese Anordnung auch schreiben als
- .
Wenden wir die Konstruktionsregel noch ein Mal auf jede mögliche Weise an, erhalten wir neben einigen ungültigen Zahlen auch die wohlgeformten surrealen Zahlen
Wir machen drei Beobachtungen:
- Wir haben vier neue Äquivalenzklassen, , , und .
- Alle Äquivalenzklassen enthalten jetzt mehr als ein Element.
- Der Wert einer surrealen Zahl hängt nur vom größten Element ihrer linken Menge und vom kleinsten Element ihrer rechten Menge ab.
Die erste Beobachtung führt uns auf die Frage, wie diese neuen Äquivalenzklassen zu interpretieren sind. Da kleiner ist als , nennen wir sie und ihre Äquivalenzklasse . Die Zahl nennen wir , liegt zwischen und und wir nennen sie , und nennen wir . Die Äquivalenzklassen schreiben wir als , , und . Eine weitere Begründung für diese Bezeichnungen erhalten wir, wenn wir die Addition und Multiplikation definiert haben.
Die zweite Beobachtung führt uns zur Frage, ob wir immer noch eine surreale Zahl mit ihrer Äquivalenzklasse identifizieren können. Die Antwort ist positiv, denn man kann zeigen:
- Wenn und , dann .
Dabei ist die Menge der Äquivalenzklassen von Elementen von . So können wir die Auflistung von oben umschreiben zu
oder kürzer
- .
Die dritte Beobachtung lässt sich auf beliebige surreale Zahlen mit endlichen linken und rechten Mengen verallgemeinern. Die oben angesprochene Zahl ist also gleich und wird später noch genauer angegeben. Unendliche Mengen müssen kein größtes Element enthalten, daher gilt für Zahlen mit unendlichen Mengen nur eine abgewandelte Aussage.
Rechnen mit surrealen Zahlen[Bearbeiten | Quelltext bearbeiten]
Die Addition und Multiplikation surrealer Zahlen wird über die folgenden drei Regeln definiert:
- Addition
- Negation
- Multiplikation
- .
Hierbei benutzen wir die mengentheoretische Erweiterung der Operatoren , d. h. es bedeuten beispielsweise
- ,
und
- .
Diese Verknüpfungen sind wohldefiniert in dem Sinne, dass die Verknüpfung von wohlgeformten surrealen Zahlen wieder eine wohlgeformte surreale Zahl ist, d. h. eine Zahl, deren linke Menge „kleiner“ als die rechte Menge ist.
Mit diesen Rechenvorschriften können wir nun feststellen, dass die bisher vergebenen Namen passen, denn es gilt zum Beispiel
- , , und .
(Man beachte die Unterscheidung zwischen der Gleichheit „“ und der Äquivalenz „“!)
Die Verknüpfungen lassen sich auf die Äquivalenzklassen übertragen, denn wegen
- Aus und folgt und und .
sind sie auch wohldefinierte Verknüpfungen der Äquivalenzklassen. Schließlich kann man zeigen, dass die Verknüpfungen der Äquivalenzklassen schöne algebraische Eigenschaften haben:
- Die Äquivalenzklassen zusammen mit der Ordnung und den algebraischen Verknüpfungen erfüllen alle Eigenschaften eines geordneten Körpers, sie sind allerdings keine Menge, sondern eine echte Klasse und deshalb im Sinne seiner Definition kein geordneter Körper.
Wir unterscheiden im Folgenden nicht mehr zwischen einer surrealen Zahl und ihrer Äquivalenzklasse, nennen also die Äquivalenzklasse selbst eine surreale Zahl.
Erzeugung durch vollständige (endliche) Induktion[Bearbeiten | Quelltext bearbeiten]
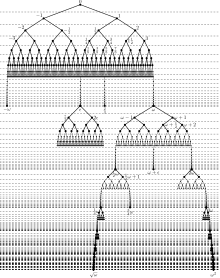
Bisher haben wir nicht systematisch danach geschaut, welche Zahlen wir durch die Konstruktionsregel erhalten und welche nicht. Wir beginnen mit den Zahlen, die wir in endlich vielen Schritten erreichen können. Das tun wir induktiv, indem wir Mengen für jede natürliche Zahl wie folgt definieren:
- ist die Menge zusammen mit allen surrealen Zahlen, die in einem Konstruktionsschritt aus Teilmengen von erzeugt werden.
Die Menge aller surrealen Zahlen, die in irgendeinem liegen, nennen wir . Die ersten Mengen von surrealen Zahlen sind
Wir beobachten zwei Dinge:
- In jedem Schritt steigt das Maximum um und sinkt das Minimum um .
- In jedem Schritt finden wir zwischen zwei benachbarten Zahlen eine neue Zahl.
Eine Folgerung davon ist, dass wir auf diese Weise genau alle dyadischen Brüche erzeugen können, d. h. jede rationale Zahl der Form
mit einer ganzen Zahl und einer natürlichen Zahl liegt in . Jedoch werden wir andere Brüche wie , , , in keinem finden, solange eine natürliche Zahl ist. Was man stattdessen für nehmen könnte, dazu kommen wir im nächsten Abschnitt.
„Ins Unendliche und darüber hinaus“[Bearbeiten | Quelltext bearbeiten]
Da wir nun eine weitere Menge von surrealen Zahlen haben, hindert uns nichts daran, die Konstruktionsregel auf sie anzuwenden und Mengen , usw. zu konstruieren. Die Mengen auf der linken und rechten Seite von surrealen Zahlen können jetzt unendlich groß werden.
Tatsächlich können wir mittels transfiniter Rekursion für jede Ordinalzahl eine Menge von surrealen Zahlen definieren.
Die kleinste Ordinalzahl , so dass eine surreale Zahl in der Menge enthalten ist, nennen wir den Geburtstag von . Zum Beispiel ist der Geburtstag von und ist der Geburtstag von .
Man kann zeigen, dass durch den Ausdruck für surreale Zahlen die „älteste“ surreale Zahl zwischen und dargestellt wird. Die oben angesprochene Zahl ist gleich und die älteste Zahl zwischen und ist die , also .
Schon in finden wir die Brüche, die uns in noch fehlten. Zum Beispiel ist
- .
Die Korrektheit dieser Definition folgt aus der Äquivalenz
- .
Der Geburtstag von ist .
In sind bereits alle reellen Zahlen enthalten. Man veranschauliche sich das mit der Tatsache, dass jede Intervallschachtelung genau eine reelle Zahl definiert und jede reelle Zahl durch Intervallschachtelungen darstellbar ist. Nun sind alle Zahlen mit der Darstellung ( beliebige ganze Zahlen) bereits in enthalten. Zudem kann man mit diesen Zahlen als Grenzen bereits für alle reellen Zahlen Intervallschachtelungen finden. Jetzt nehme man die unteren Grenzen dieser Intervallschachtelung in die linke Menge und die oberen Grenzen der Intervallschachtelung in die rechte Menge und schon hat man die gewünschte reelle Zahl als Bestandteil von .
Eine andere Zahl, die in liegt, ist
- .
Man erkennt leicht, dass diese Zahl größer ist als , aber kleiner als jeder positive Bruch. Es handelt sich hierbei also um eine infinitesimale Zahl. Wir bezeichnen ihre Äquivalenzklasse deshalb mit . Dies ist nicht die einzige infinitesimale Zahl, denn es gilt z. B.
- ,
- .
Diese Zahlen liegen jedoch erst in .
Neben unendlich kleinen Zahlen sind auch unendlich große Zahlen in zu finden, wie z. B.
- .
Diese Zahl ist größer als jede Zahl in , insbesondere größer als jede natürliche Zahl, ihre Äquivalenzklasse bezeichnen wir daher mit . Diese Zahl entspricht der Ordinalzahl . Es ist auch
- .
Man kann sogar jede Ordinalzahl als surreale Zahl darstellen.
Da Addition und Subtraktion für alle surrealen Zahlen erklärt sind, können wir mit rechnen wie mit jeder anderen Zahl und z. B. Folgendes berechnen:
- und
- .
Das geht auch für größere Summanden:
- ,
- ,
- ,
und sogar mit selbst:
wobei wie oben.
So wie größer ist als , ist kleiner als , denn
wobei .
Schließlich finden wir einen engen Zusammenhang zwischen und , denn es ist
- .
Zu beachten ist aber, dass die Rechenregeln für Ordinalzahlen sich unterscheiden von denen der surrealen Darstellungen: In den Ordinalzahlen gilt , als surreale Zahl ist jedoch .
Sehr viele Zahlen können auf diese Weise erzeugt werden, sogar so viele, dass keine Menge sie alle aufnehmen kann. Die surrealen Zahlen bilden wie die Ordinalzahlen eine echte Klasse.
Da jede surreale Zahl aus surrealen Zahlen zusammengesetzt ist, die einen kleineren Geburtstag haben, kann man fast alle Aussagen über surreale Zahlen per transfiniter Induktion beweisen. Man zeigt dazu, dass eine Aussage für gilt, falls sie für jedes Element von und gilt.
Mengentheoretische Bemerkung[Bearbeiten | Quelltext bearbeiten]
Wie im Abschnitt Rechnen mit surrealen Zahlen bereits erwähnt, bilden die surrealen Zahlen eine echte Klasse, also keine Menge im Sinne einer üblichen Mengenlehre wie der Zermelo-Fraenkel-Mengenlehre. Der Grund ist, dass jede Ordinalzahl als surreale Zahl darstellbar ist und die Ordinalzahlen bereits eine echte Klasse bilden. Die Definition einer Surrealzahl als Paar von Linksmenge und Rechtsmenge von Surrealzahlen schließt aus, dass auch eine dieser Mengen eine echte Klasse sein könnte, da Mengen keine echten Klassen sein können.
Verallgemeinerung: Games[Bearbeiten | Quelltext bearbeiten]
Die Definition einer surrealen Zahl enthielt eine Einschränkung: Jedes Element von muss kleiner sein als jedes Element von . Wenn man diese Einschränkung fallen lässt, erhält man eine größere Klasse von Objekten, die Games (engl. für Spiele) genannt werden. Ein Game entsteht durch Anwendung dieser Regel:
- Konstruktionsregel
- Sind und zwei Mengen von Games, dann ist ein Game.
Vergleich, Äquivalenz, Addition, Negation und Multiplikation werden genauso wie für surreale Zahlen definiert.
Jede surreale Zahl ist ein Game, aber es gibt auch nicht wohlgeformte Games, wie z. B. . Die Klasse der Games ist allgemeiner als die der surrealen Zahlen und hat eine einfachere Definition, jedoch fehlen ihr einige der schönen Eigenschaften der surrealen Zahlen. Die Games bilden keinen Körper. Sie haben nur eine partielle Ordnung, d. h. es gibt Games, die nicht vergleichbar sind. Jede surreale Zahl ist entweder größer, gleich oder kleiner als , aber ein Game ist entweder größer, gleich, kleiner als oder unvergleichbar mit (engl. fuzzy). Sind , , surreale Zahlen und , dann ist . Sind , , dagegen Games mit , dann gilt nicht immer .
Surreale Zahlen und Spieltheorie[Bearbeiten | Quelltext bearbeiten]
Die surrealen Zahlen wurden ursprünglich motiviert durch das Studium des Spiels Go, und es gibt viele Verbindungen zwischen bekannten Spielen und surrealen Zahlen.
Wir betrachten Spiele mit folgenden Eigenschaften:
- Zwei Spieler, genannt Links und Rechts
- Deterministisch (kein Würfel oder gemischte Karten)
- Keine versteckte Information (wie z. B. verdeckte Spielkarten)
- Die Spieler ziehen abwechselnd.
- Jede Partie endet nach endlich vielen Zügen mit dem Sieg eines Spielers.
- Kann ein Spieler keinen Zug mehr machen, endet das Spiel und dieser Spieler verliert (möglicherweise endet das Spiel beim Schach unentschieden).
Solche Spiele sind Schach, Dame, Mühle und Go, jedoch nicht die meisten Kartenspiele, Memory oder „Mensch ärgere dich nicht“.
Bei den meisten Spielen hat anfangs keiner der Spieler einen großen Vorteil. Schreitet die Partie jedoch voran, dann treten irgendwann Situationen auf, in denen einer der Spieler einen klaren Vorteil hat. Um ein Spiel zu analysieren, ordnet man nun jeder möglichen Spielsituation ein Game zu. Der Wert einer Spielposition ist das Game , wobei die Werte aller Positionen enthält, die durch einen Zug von Links erreicht werden können, und die Werte aller Positionen, die durch einen Zug von Rechts erreicht werden können. Diese einfache Art, Games mit Spielpositionen zu verknüpfen, liefert interessante Resultate. Nehmen wir an, zwei perfekte Spieler befinden sich in einer Spielsituation, deren Game ist. Dann steht der Gewinner der Partie fest:
- Ist , dann gewinnt Links,
- ist , dann gewinnt Rechts,
- ist , dann verliert der Spieler, der am Zug ist,
- ist fuzzy, dann gewinnt der Spieler, der am Zug ist.
Manchmal, wenn eine Partie sich dem Ende nähert, zerfällt sie in kleinere Teilpartien, die völlig unabhängig sind. Beim Spiel Go zum Beispiel wird das Spielbrett nach und nach unter den Parteien aufgeteilt, bis nur noch kleine, getrennte Inseln von neutralem Raum verbleiben, in dem die Spieler setzen können. Jede Insel verhält sich wie eine eigene Go-Partie auf einem sehr kleinen Brett. Es wäre nun nützlich, jede Teilpartie einzeln zu analysieren und dann die Ergebnisse kombinieren zu können, um so eine Analyse der gesamten Partie zu bekommen. Das ist keine leichte Aufgabe. Zum Beispiel könnte man zwei Teilpartien haben, in denen jeweils der Anziehende gewinnt, aber betrachtet man beide Partien zusammen, gewinnt der andere Spieler. Jedoch gibt es einen Weg, diese Analyse durchzuführen, und zwar durch das folgende Theorem:
- Wenn eine große Partie in zwei kleinere, unabhängige Partien zerfällt und die beiden Partien die Games und haben, dann hat die große Partie das Game .
Mit anderen Worten: Mehrere unabhängige Partien zusammenzufassen entspricht der Addition ihrer Games.
Geschichtliche Entwicklung[Bearbeiten | Quelltext bearbeiten]
Conway entwickelte die Theorie der surrealen Zahlen in der umgekehrten Reihenfolge zur hier gewählten Darstellung. Er analysierte Endspiele beim Go und suchte nach einem Weg, die Analysen von unabhängigen Teilpartien zu kombinieren. So entwickelte er das auch als Kombinatorische Spieltheorie bezeichnete Konzept der Games mit den Möglichkeiten der Addition, Negation und eines Größenvergleichs. Schließlich bemerkte er, dass eine bestimmte Klasse von Games (die später surreale Zahlen genannt wurden) interessante Eigenschaften hat und fand für sie eine Multiplikation, die die Körperaxiome erfüllt und mit der sie die reellen Zahlen enthalten.





























![{\textstyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c30fa8e7afcea4b0e44d43a42568446b8e1b0d1)
![{\textstyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9a815121008270b9c567aad77310133d00bada4)


![{\textstyle [\mathbf {0} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8356afb4af8e403319fcfb4a82a35920191015d6)



















![{\textstyle [\lbrace \,\mid \mathbf {-1} \,\rbrace ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2dbadebdad583888398b677386a755d4b07f8c7)
![{\textstyle [\lbrace \,\mathbf {-1} \mid \mathbf {0} \,\rbrace ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f98210104476a68a0c4c7c1688da70c4445483a)
![{\textstyle [\lbrace \,\mathbf {0} \mid \mathbf {1} \,\rbrace ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f2fbdfcbbf6b257dba822e8a3bc3a8362ac44cb)
![{\textstyle [\lbrace \,\mathbf {1} \mid \,\rbrace ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/539e45246557a7ed9a41c6b8c988b0a26a0175cd)











![{\textstyle [L_{x}]=[L_{y}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560ec2fc36e74672ec8d84692bc7a1101ad273a1)
![{\textstyle [R_{x}]=[R_{y}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b6a646383f7716d3c799c363e145917ddcd2d42)
![{\textstyle [\lbrace \,L_{x}\mid R_{x}\,\rbrace ]=[\lbrace \,L_{y}\mid R_{y}\,\rbrace ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6143fdb8b6d4fffef5dc3b10c0314976a42e916)
![{\textstyle [X]=\lbrace \,[x]\colon x\in X\,\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/654a2904ff471ca6d3415686588b857ae6e1d377)























![{\textstyle [x]=[x']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75fb0076cf445fd9075f2c23b5f3acfc8a63c694)
![{\textstyle [y]=[y']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4e78b79c4d7190005122029d8c404b9a0ea169a)
![{\textstyle [x+y]=[x'+y']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d888097e9e4abf03afd51ee5bc56f78101d5d6f)
![{\textstyle [-x]=[-x']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/127f883841e0a0d6ac915ffc2a5d1d50c35718bb)
![{\textstyle [x\cdot y]=[x'\cdot y']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad4d29b9efe0f45fa33cf8d7a5c0f3e6510122f)





























































