Dieser Artikel beschreibt eine
spezielle Funktion . Für die Formel, die die Transmission von elektromagnetischer Strahlung beschreibt siehe
Airy-Formel .
Die Airy-Funktion
Ai
(
x
)
{\displaystyle \operatorname {Ai} (x)}
spezielle Funktion in der Mathematik. Die Funktion
Ai
(
x
)
{\displaystyle \operatorname {Ai} (x)}
Bi
(
x
)
{\displaystyle \operatorname {Bi} (x)}
linearen Differentialgleichung
y
″
−
x
y
=
0
,
{\displaystyle \ y''-xy=0\ ,}
auch bekannt als Airy-Gleichung. Sie beschreibt unter anderem die Lösung der Schrödinger-Gleichung für einen linearen Potentialtopf .
Die Airy-Funktion ist nach dem britischen Astronomen George Biddell Airy benannt, der diese Funktion in seinen Arbeiten in der Optik verwendete (Airy 1838). Die Bezeichnung
Ai
(
x
)
{\displaystyle \operatorname {Ai} (x)}
Harold Jeffreys eingeführt.
Für reelle Werte
x
{\displaystyle x}
Parameterintegral definiert:
A
i
(
x
)
=
1
π
∫
0
∞
cos
(
t
3
3
+
x
t
)
d
t
.
{\displaystyle \mathrm {Ai} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)\,{\rm {d}}t\ .}
Eine zweite, linear unabhängige Lösung der Differentialgleichung ist die Airy-Funktion zweiter Art
B
i
{\displaystyle \mathrm {Bi} }
B
i
(
x
)
=
1
π
∫
0
∞
(
exp
(
−
t
3
3
+
x
t
)
+
sin
(
t
3
3
+
x
t
)
)
d
t
.
{\displaystyle \mathrm {Bi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\left(\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\right)\,{\rm {d}}t\ .}
Die komplexe Airy-Funktion ist
Ai
(
z
)
=
1
2
π
i
∫
C
exp
(
t
3
3
−
z
t
)
d
t
,
{\displaystyle \operatorname {Ai} (z)={\frac {1}{2\pi i}}\int _{C}\exp \left({\tfrac {t^{3}}{3}}-zt\right)\,dt,}
mit Kontour
C
{\displaystyle C}
z
1
=
∞
{\displaystyle z_{1}=\infty }
arg
(
z
1
)
=
−
π
/
3
{\displaystyle \operatorname {arg} (z_{1})=-\pi /3}
z
2
=
∞
{\displaystyle z_{2}=\infty }
arg
(
z
2
)
=
π
/
3
{\displaystyle \operatorname {arg} (z_{2})=\pi /3}
Für
x
{\displaystyle x}
+
∞
{\displaystyle +\infty }
A
i
(
x
)
{\displaystyle \mathrm {Ai} (x)}
B
i
(
x
)
{\displaystyle \mathrm {Bi} (x)}
WKB-Näherung approximieren:
A
i
(
x
)
≃
e
−
2
3
x
3
/
2
2
π
x
1
/
4
B
i
(
x
)
≃
e
2
3
x
3
/
2
π
x
1
/
4
.
{\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}\simeq {\frac {e^{-{\frac {2}{3}}x^{3/2}}}{2{\sqrt {\pi }}\,x^{1/4}}}\\\mathrm {Bi} (x)&{}\simeq {\frac {e^{{\frac {2}{3}}x^{3/2}}}{{\sqrt {\pi }}\,x^{1/4}}}.\end{aligned}}}
Für
x
{\displaystyle x}
−
∞
{\displaystyle -\infty }
A
i
(
x
)
≃
sin
(
2
3
(
−
x
)
3
/
2
+
1
4
π
)
π
(
−
x
)
1
/
4
B
i
(
x
)
≃
cos
(
2
3
(
−
x
)
3
/
2
+
1
4
π
)
π
(
−
x
)
1
/
4
.
{\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}\simeq {\frac {\sin({\frac {2}{3}}(-x)^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,(-x)^{1/4}}}\\\mathrm {Bi} (x)&{}\simeq {\frac {\cos({\frac {2}{3}}(-x)^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,(-x)^{1/4}}}.\end{aligned}}}
Die Airy-Funktionen haben nur Nullstellen auf der negativen reellen Achse.[ 1]
x
→
−
∞
{\displaystyle x\to -\infty }
Ai
(
x
)
=
0
⇒
x
≈
−
(
3
2
π
(
n
−
1
4
)
)
2
/
3
,
n
∈
N
{\displaystyle \operatorname {Ai} (x)=0\quad \Rightarrow \quad x\approx -{\bigl (}\textstyle {\frac {3}{2}}\pi (n-{\frac {1}{4}}){\bigr )}^{2/3},\quad n\in \mathbb {N} }
Bi
(
x
)
=
0
⇒
x
≈
−
(
3
2
π
(
n
−
3
4
)
)
2
/
3
,
n
∈
N
{\displaystyle \operatorname {Bi} (x)=0\quad \Rightarrow \quad x\approx -{\bigl (}\textstyle {\frac {3}{2}}\pi (n-{\frac {3}{4}}){\bigr )}^{2/3},\quad n\in \mathbb {N} }
Die Airy-Funktionen und ihre Ableitungen haben für
x
=
0
{\displaystyle x=0}
A
i
(
0
)
=
1
9
3
⋅
Γ
(
2
3
)
,
A
i
′
(
0
)
=
−
1
3
3
⋅
Γ
(
1
3
)
,
B
i
(
0
)
=
1
3
6
⋅
Γ
(
2
3
)
,
B
i
′
(
0
)
=
3
6
Γ
(
1
3
)
.
{\displaystyle {\begin{aligned}\mathrm {Ai} (0)&{}={\frac {1}{{\sqrt[{3}]{9}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Ai} '(0)&{}=-{\frac {1}{{\sqrt[{3}]{3}}\cdot \Gamma ({\frac {1}{3}})}},\\\mathrm {Bi} (0)&{}={\frac {1}{{\sqrt[{6}]{3}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Bi} '(0)&{}={\frac {\sqrt[{6}]{3}}{\Gamma ({\frac {1}{3}})}}.\end{aligned}}}
Hierbei bezeichnet
Γ
(
⋅
)
{\displaystyle \Gamma (\cdot )}
Gammafunktion . Es folgt, dass die Wronski-Determinante von
A
i
(
x
)
{\displaystyle \mathrm {Ai} (x)}
B
i
(
x
)
{\displaystyle \mathrm {Bi} (x)}
1
π
{\displaystyle {\tfrac {1}{\pi }}}
Direkt aus der Definition der Airy-Funktion
Ai
(
x
)
{\displaystyle \operatorname {Ai} (x)}
Fourier-Transformierte .
F
(
Ai
)
(
k
)
:=
∫
−
∞
∞
Ai
(
x
)
e
−
2
π
i
k
x
d
x
=
e
i
3
(
2
π
k
)
3
.
{\displaystyle {\mathcal {F}}(\operatorname {Ai} )(k):=\int _{-\infty }^{\infty }\operatorname {Ai} (x)\ \mathrm {e} ^{-2\pi \mathrm {i} kx}\,dx=\mathrm {e} ^{{\frac {\mathrm {i} }{3}}(2\pi k)^{3}}\,.}
Man beachte die hier verwendete symmetrische Variante der Fourier-Transformation.
A
i
(
z
)
=
1
3
2
/
3
⋅
Γ
(
2
3
)
⋅
0
F
1
(
0
;
2
3
;
1
9
z
3
)
−
z
3
1
/
3
⋅
Γ
(
1
3
)
⋅
0
F
1
(
0
;
4
3
;
1
9
z
3
)
{\displaystyle \mathrm {Ai} (z)={\frac {1}{3^{2/3}\cdot \Gamma ({\tfrac {2}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {2}{3}};{\tfrac {1}{9}}z^{3}\right)-{\frac {z}{3^{1/3}\cdot \Gamma ({\tfrac {1}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {4}{3}};{\tfrac {1}{9}}z^{3}\right)}
B
i
(
z
)
=
1
3
1
/
6
⋅
Γ
(
2
3
)
⋅
0
F
1
(
0
;
2
3
;
1
9
z
3
)
+
3
1
/
6
⋅
z
Γ
(
1
3
)
⋅
0
F
1
(
0
;
4
3
;
1
9
z
3
)
{\displaystyle \mathrm {Bi} (z)={\frac {1}{3^{1/6}\cdot \Gamma ({\tfrac {2}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {2}{3}};{\tfrac {1}{9}}z^{3}\right)+{\frac {3^{1/6}\cdot z}{\Gamma ({\tfrac {1}{3}})}}\cdot \,{}_{0}F_{1}\left(0;{\tfrac {4}{3}};{\tfrac {1}{9}}z^{3}\right)}
A
i
(
x
)
=
1
3
x
[
I
−
1
/
3
(
2
3
x
3
/
2
)
−
I
1
/
3
(
2
3
x
3
/
2
)
]
{\displaystyle \mathrm {Ai} (x)={\frac {1}{3}}{\sqrt {x}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)-I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}
B
i
(
x
)
=
x
3
[
I
−
1
/
3
(
2
3
x
3
/
2
)
+
I
1
/
3
(
2
3
x
3
/
2
)
]
{\displaystyle \mathrm {Bi} (x)={\sqrt {\frac {x}{3}}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)+I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}
Eine andere unendliche Integraldarstellung für
A
i
{\displaystyle \mathrm {Ai} }
A
i
(
z
)
=
1
2
π
∫
−
∞
∞
exp
(
i
⋅
(
z
t
+
t
3
3
)
)
d
t
{\displaystyle \mathrm {Ai} (z)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }\exp \left(\mathrm {i} \cdot \left(zt+{\frac {t^{3}}{3}}\right)\right)\mathrm {d} t}
Es gibt die Reihendarstellungen[ 2]
A
i
(
z
)
=
1
3
2
/
3
π
∑
n
=
0
∞
Γ
(
1
3
(
n
+
1
)
)
n
!
(
3
1
/
3
z
)
n
sin
(
2
(
n
+
1
)
π
3
)
{\displaystyle \mathrm {Ai} (z)={\frac {1}{3^{2/3}\pi }}\sum _{n=0}^{\infty }{\frac {\Gamma \left({\frac {1}{3}}(n+1)\right)}{n!}}\left(3^{1/3}z\right)^{n}\sin \left({\frac {2(n+1)\pi }{3}}\right)}
B
i
(
z
)
=
1
3
1
/
6
π
∑
n
=
0
∞
Γ
(
1
3
(
n
+
1
)
)
n
!
(
3
1
/
3
z
)
n
|
sin
(
2
(
n
+
1
)
π
3
)
|
{\displaystyle \mathrm {Bi} (z)={\frac {1}{3^{1/6}\pi }}\sum _{n=0}^{\infty }{\frac {\Gamma \left({\frac {1}{3}}(n+1)\right)}{n!}}\left(3^{1/3}z\right)^{n}\left|\sin \left({\frac {2(n+1)\pi }{3}}\right)\right|}
A
i
(
x
)
{\displaystyle \mathrm {Ai} (x)}
B
i
(
x
)
{\displaystyle \mathrm {Bi} (x)}
ganze Funktionen . Sie lassen sich also auf der gesamten komplexen Ebene analytisch fortsetzen.
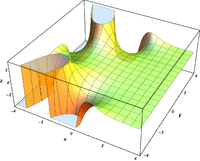
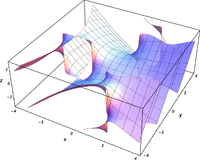
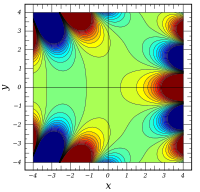
ℜ
[
A
i
(
x
+
i
y
)
]
{\displaystyle \Re \left[\mathrm {Ai} (x+iy)\right]}
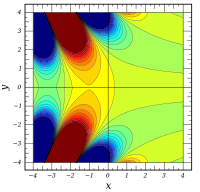
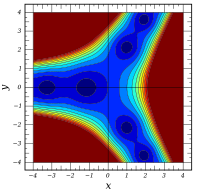
ℑ
[
A
i
(
x
+
i
y
)
]
{\displaystyle \Im \left[\mathrm {Ai} (x+iy)\right]}
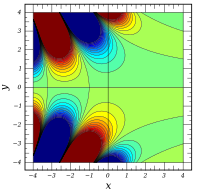
|
A
i
(
x
+
i
y
)
|
{\displaystyle |\mathrm {Ai} (x+iy)|\,}
a
r
g
[
A
i
(
x
+
i
y
)
]
{\displaystyle \mathrm {arg} \left[\mathrm {Ai} (x+iy)\right]\,}
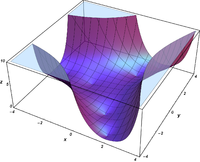
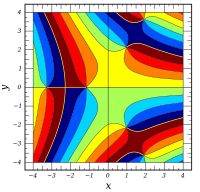
ℜ
[
B
i
(
x
+
i
y
)
]
{\displaystyle \Re \left[\mathrm {Bi} (x+iy)\right]}
ℑ
[
B
i
(
x
+
i
y
)
]
{\displaystyle \Im \left[\mathrm {Bi} (x+iy)\right]}
|
B
i
(
x
+
i
y
)
|
{\displaystyle |\mathrm {Bi} (x+iy)|\,}
a
r
g
[
B
i
(
x
+
i
y
)
]
{\displaystyle \mathrm {arg} \left[\mathrm {Bi} (x+iy)\right]\,}
Definiere
T
n
(
t
,
α
)
=
t
n
2
F
1
(
−
n
2
,
1
−
n
2
;
1
−
n
;
−
4
α
t
2
)
{\displaystyle T_{n}(t,\alpha )=t^{n}{}_{2}F_{1}\left(-{\frac {n}{2}},{\frac {1-n}{2}};1-n;-{\frac {4\alpha }{t^{2}}}\right)}
wobei
2
F
1
{\displaystyle {}_{2}F_{1}}
hypergeometrische Funktion ist.
Dann gibt es folgende Verallgemeinerungen des Airy-Integrals
Ci
n
(
α
)
=
∫
0
∞
cos
(
T
n
(
t
,
α
)
)
d
t
{\displaystyle \operatorname {Ci} _{n}(\alpha )=\int _{0}^{\infty }\cos(T_{n}(t,\alpha ))\mathrm {d} t}
Si
n
(
α
)
=
∫
0
∞
sin
(
T
n
(
t
,
α
)
)
d
t
{\displaystyle \operatorname {Si} _{n}(\alpha )=\int _{0}^{\infty }\sin(T_{n}(t,\alpha ))\mathrm {d} t}
Ei
n
(
α
)
=
∫
0
∞
exp
(
−
T
n
(
t
,
α
)
)
d
t
{\displaystyle \operatorname {Ei} _{n}(\alpha )=\int _{0}^{\infty }\exp(-T_{n}(t,\alpha ))\mathrm {d} t}
Zu der Airy-Funktion lässt sich analog zu den anderen Zeta-Funktionen die Airysche Zeta-Funktion definieren als[ 3]
Z
(
n
)
=
∑
r
1
r
n
,
{\displaystyle Z(n)=\sum _{r}{\frac {1}{r^{n}}},}
wobei die Summe über die reellen (negativen) Nullstellen von
A
i
{\displaystyle \mathrm {Ai} }
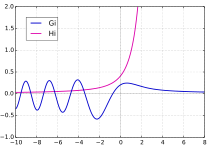
Funktionsgraphen von
G
i
(
x
)
{\displaystyle \mathrm {Gi} (x)}
H
i
(
x
)
{\displaystyle \mathrm {Hi} (x)}
Manchmal werden auch die beiden weiteren Funktionen
G
i
(
x
)
{\displaystyle \mathrm {Gi} (x)}
H
i
(
x
)
{\displaystyle \mathrm {Hi} (x)}
[ 4]
G
i
(
x
)
=
1
π
∫
0
∞
sin
(
t
3
3
+
x
t
)
d
t
{\displaystyle \mathrm {Gi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\sin \left({\frac {t^{3}}{3}}+xt\right)\,\mathrm {d} t}
H
i
(
x
)
=
1
π
∫
0
∞
exp
(
−
t
3
3
+
x
t
)
d
t
{\displaystyle \mathrm {Hi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\exp \left(-{\frac {t^{3}}{3}}+xt\right)\,\mathrm {d} t}
Sie lassen sich auch durch die Funktionen
A
i
{\displaystyle \mathrm {Ai} }
B
i
{\displaystyle \mathrm {Bi} }
↑ Eric W. Weisstein : Airy Function Zeros .MathWorld ↑ C. Banderier, P. Flajolet, G. Schaeffer, M. Soria: Planar Maps and Airy Phenomena. In Automata, Languages and Programming. Proceedings of the 27th International Colloquium (ICALP 2000) held at the University of Geneva , Geneva, 9.–15. Juli 2000 (Ed. U. Montanari, J. D. P. Rolim, E. Welzl). Berlin: Springer, S. 388–402, 2000
↑ Eric W. Weisstein : Airy Zeta Function .MathWorld ↑ Milton Abramowitz und Irene A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Seite 447
































![{\displaystyle {\begin{aligned}\mathrm {Ai} (0)&{}={\frac {1}{{\sqrt[{3}]{9}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Ai} '(0)&{}=-{\frac {1}{{\sqrt[{3}]{3}}\cdot \Gamma ({\frac {1}{3}})}},\\\mathrm {Bi} (0)&{}={\frac {1}{{\sqrt[{6}]{3}}\cdot \Gamma ({\frac {2}{3}})}},&\quad \mathrm {Bi} '(0)&{}={\frac {\sqrt[{6}]{3}}{\Gamma ({\frac {1}{3}})}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85175b026a300ea1e494ba99b326df0e329f29f)








![{\displaystyle \mathrm {Ai} (x)={\frac {1}{3}}{\sqrt {x}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)-I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1f0cd33e711461cb3ab410a2d4b0af8dcb99aca)
![{\displaystyle \mathrm {Bi} (x)={\sqrt {\frac {x}{3}}}\left[I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)+I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9175279c9f086c7d1242484b4430f327531ed036)




![{\displaystyle \Re \left[\mathrm {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/505e2f06e2e8d14027c46f1f4b1ac72367f85b58)
![{\displaystyle \Im \left[\mathrm {Ai} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c4ca8fdfe9c79b62f9becbb2687b12f68d42e18)

![{\displaystyle \mathrm {arg} \left[\mathrm {Ai} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/190234ee42ad7ac3a352d501c46e3bfcb4e64be4)
![{\displaystyle \Re \left[\mathrm {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a86d49867d1f711cbe25936ea7982c44f005c53)
![{\displaystyle \Im \left[\mathrm {Bi} (x+iy)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b658626fb2e88ae1d2a3ff37af457b29b0f17e0d)

![{\displaystyle \mathrm {arg} \left[\mathrm {Bi} (x+iy)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e6398901714ff29a82ca26b13f90f473377a731)









