Anwendung von Gaußprozessen
Technische Anwendungen von Gaußprozessen findet man unter anderem in der Numerik, Informatik und speziell im Bereich des maschinellen Lernens. Sie stellen dort ein vielseitiges Werkzeug zum Umgang mit realen Messdaten und zur Modellierung von Funktionen dar.
Einleitung
[Bearbeiten | Quelltext bearbeiten]Ein Gaußprozess ist ein stochastischer Prozess mit der Eigenschaft, dass jede endliche Teilmenge seiner Werte mehrdimensional normalverteilt (gaußverteilt) ist. Als stochastischen Prozess bezeichnet man eine Funktion, deren Werte Zufallsvariablen sind und die einer vorgegebenen Wahrscheinlichkeitsverteilung folgen. Damit lassen sich Funktionen mit Wahrscheinlichkeiten modellieren, deren Werte aus einem Mangel an Information nicht vollständig festgelegt werden können. Einen Gaußprozess konstruiert man aus Funktionen der Erwartungswerte, Varianzen und Kovarianzen und beschreibt damit die Funktionswerte als ein Kontinuum aus im Allgemeinen korrelierten Zufallsvariablen in Form einer unendlichdimensionalen Normalverteilung. Die Verteilung eines Gaußprozesses kann man sich als eine Wahrscheinlichkeitsverteilung für Funktionen vorstellen. Eine Stichprobe davon ergibt eine zufällige Funktion mit bestimmten bevorzugten Eigenschaften seiner Kurvenform.
Anwendungen
[Bearbeiten | Quelltext bearbeiten]Angewendet werden Gaußprozesse zur mathematischen Modellierung des Verhaltens von nicht-deterministischen Systemen auf der Basis von stochastischen Größen oder Beobachtungen. Gaußprozesse eignen sich zur Signalanalyse und -synthese, bilden ein mächtiges Werkzeug bei der Interpolation, Extrapolation oder Glättung beliebig-dimensionaler diskreter Messpunkte (Gaußprozess-Regression bzw. Kriging-Verfahren) und finden Anwendung in Klassifizierungsproblemen. Gaußprozesse, die mit Kernel-Methoden verwandt sind,[1] können wie ein überwachtes Maschinenlernverfahren zur abstrakten Modellierung anhand von Trainingsbeispielen verwendet werden. Dieser bayessche Ansatz des maschinellen Lernens bietet den Vorteil, dass häufig kein iteratives Training wie bei neuronalen Netzen notwendig ist. Stattdessen können Gaußprozesse sehr effizient mit linearer Algebra aus statistischen Größen der Beispiele abgeleitet werden und sind dabei mathematisch klar interpretierbar und gut kontrollierbar. Außerdem wird bei Interpolationen und Vorhersagen für jeden einzelnen Ausgabewert ein zugehöriges Vertrauensintervall berechnet, das den eigenen Vorhersagefehler präzise schätzt, während die Fehlerfortpflanzung bei bekannter Varianz der Eingabewerte korrekt berücksichtigt wird.
Mathematische Beschreibung
[Bearbeiten | Quelltext bearbeiten]Definition
[Bearbeiten | Quelltext bearbeiten]Ein Gaußprozess ist ein spezieller stochastischer Prozess auf einer beliebigen Indexmenge , wenn seine endlichdimensionalen Verteilungen mehrdimensionale Normalverteilungen (auch Gaußverteilungen) sind. Es soll also für alle und alle Indizes die multivariate Verteilung von durch eine -dimensionale Normalverteilung gegeben sein.
Begriff: Obwohl der Begriff Gaußprozess auf zeitliche oder sequenzielle Vorgänge hindeutet, besteht diese Einschränkung nicht. Im verallgemeinerten Sinn kann Prozess auch als Kontinuum verstanden werden.
Notation
[Bearbeiten | Quelltext bearbeiten]Analog zur ein- und mehrdimensionalen Gaußverteilung ist ein Gaußprozess über seine ersten beiden Momente vollständig und eindeutig bestimmt. Bei der mehrdimensionalen Gaußverteilung sind dies der Erwartungswertvektor und die Kovarianzmatrix . Beim Gaußprozess treten an deren Stelle eine Erwartungswertfunktion
und eine Kovarianzfunktion
- .
Diese Funktionen können im einfachsten eindimensionalen Fall als Vektor mit kontinuierlichen Zeilen bzw. als Matrix mit kontinuierlichen Zeilen und Spalten aufgefasst werden. Folgende Tabelle vergleicht die Notationen von eindimensionalen und mehrdimensionalen Gaußverteilungen mit der von Gaußprozessen. In manchen Fällen ist die Angabe einer Wahrscheinlichkeitsdichtefunktion möglich. Das Tilde-Symbol kann gelesen werden als „Ist verteilt als“.
| Art der Verteilung | Notation | Größen | Wahrscheinlichkeitsdichtefunktion |
|---|---|---|---|
| Eindimensionale Gaußverteilung | |||
| Mehrdimensionale Gaußverteilung | |||
| Gaußprozess-Verteilung | (keine analytische Darstellung) |
Die Wahrscheinlichkeitsdichtefunktion eines Gaußprozesses lässt sich nicht analytisch darstellen, da es keine entsprechende Notation für Operationen mit kontinuierlichen Matrizen gibt. Das erweckt den Eindruck, dass man mit Verteilungen von Gaußprozessen nicht wie mit endlichdimensionalen Normalverteilungen rechnen kann. Jedoch ist die wesentliche Eigenschaft von Gaußprozessen in der Anwendung weniger die Unendlichkeit der Dimensionen, sondern vielmehr die Zuordnung der Dimensionen zu den Koordinaten einer Funktion. In praktischen Anwendungen hat man es immer nur mit endlich vielen Stützstellen zu tun und kann daher alle Berechnungen wie im endlichdimensionalen Fall durchführen. Der Grenzwert für unendlich viele Dimensionen wird dabei nur in einem Zwischenschritt benötigt, nämlich dann, wenn Werte an neuen interpolierten Stützstellen geschätzt werden sollen. In diesem Zwischenschritt wird der Gaußprozess, d. h. die Erwartungswertfunktion und Kovarianzfunktion, durch geeignete analytische Ausdrücke dargestellt bzw. approximiert. Dabei erfolgt die Zuordnung zu den Stützstellen über die parametrisierten Koordinaten im analytischen Ausdruck. Im endlichdimensionalen Fall mit diskreten Stützstellen werden die zugehörigen Koordinaten den Dimensionen über ihre Indizes zugeordnet.
Beispiel eines Gaußprozesses
[Bearbeiten | Quelltext bearbeiten]Als ein einfaches Beispiel sei ein Gaußprozess
mit einer skalaren Variable (Zeit) durch die Erwartungswertfunktion
und Kovarianzfunktion
gegeben. Dieser Gaußprozess beschreibt ein endloses zeitliches elektrisches Signal mit gaußschem weißen Rauschen mit einer Standardabweichung von einem Volt um eine mittlere Spannung von 5 Volt.
Definitionen spezieller Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Ein Gaußprozess heißt zentriert, wenn sein Erwartungswert konstant Null ist, also wenn für alle .
Eine Kovarianzfunktion heißt stationär wenn sie translationsinvariant ist und durch eine relative Funktion beschrieben werden kann.[2]
Ein Gaußprozess heißt stationär (oder translationsinvariant), wenn seine Kovarianzfunktion stationär und sein Erwartungswert konstant ist.[3]
Ein Kovarianzfunktion heißt radial, wenn radialsymmetrisch ist mit der Euklidischen Norm . Stationäre Gaußprozesse mit dieser Eigenschaft können Systeme mit isotropen Modell-Eigenschaften beschreiben.
Liste gängiger Gaußprozesse und Kovarianzfunktionen
[Bearbeiten | Quelltext bearbeiten]- Konstant: und
- Entspricht einem konstanten Wert aus einer Gaußverteilung mit Standardabweichung .
- Offset: und
- Entspricht einem konstanten Wert, der durch fest vorgegeben ist.
- Gaußsches Weißes Rauschen:
- (: Standardabweichung, : Kronecker-Delta)
- Rational quadratisch:
- Gamma-Exponentiell:
- Ornstein-Uhlenbeck:[4]
- Entspricht einem einfachen Gauß-Markov-Prozess und beschreibt stetige, nicht-differenzierbare Funktionen, außerdem weißes Rauschen, nachdem es einen RC-Tiefpass-Filter durchlaufen hat.
- Quadratisch exponentiell:
- Beschreibt glatte unendlich oft differenzierbare Funktionen.
- Matérn: [5]
- Sehr universell verwendbare Gaußprozesse zur Beschreibung der meisten typischen Messkurven. Die Funktionen des Gaußprozesses sind -mal stetig differenzierbar, wenn . Kovarianzfunktionen mit , , usw. entsprechen weißem Rauschen, welches 1, 2 oder 3 RC-Tiefpass-Filter durchlaufen hat bzw. entsprechend oft mit der Funktion gefaltet wurde. Gängige Spezialfälle sind:
- entspricht der Ornstein-Uhlenbeck-Kovarianzfunktion und der quadratisch exponentiellen.
- Periodisch:
- Funktionen von diesem Gaußprozess sind sowohl periodisch mit der Periodendauer als auch glatt (quadratisch exponentiell). Wird das Quadrat um den Sinus durch den Betrag ersetzt, ergeben sich nicht-glatte periodische Funktionen.
- Polynomial:
- Wächst nach außen stark an und ist meist eine schlechte Wahl bei Regressionsproblemen, kann aber bei hochdimensionalen Klassifizierungsproblemen nützlich sein. Sie ist positiv semidefinit und erzeugt nicht notwendigerweise invertierbare Kovarianzmatrizen.[6]
- Brownsche Brücke: und
- Wiener-Prozess: und
- Entspricht der Brownschen Bewegung bzw. dem Integral über gaußsches weißes Rauschen.
Bemerkungen:
- ist die Distanz bei stationären und radialen Kovarianzfunktionen
- ist die charakteristische Längenskala der Kovarianzfunktion, bei der die Korrelation auf etwa abgefallen ist.
- Die meisten stationären Kovarianzfunktionen werden auf normiert notiert und sind somit gleichbedeutend zu Korrelationsfunktionen. Für den Gebrauch als Kovarianzfunktion werden sie mit einer Varianz multipliziert, was den Variablen eine Skalierung und/oder physikalische Einheit zuordnet.
- Kovarianzfunktionen dürfen nicht beliebige Funktionen oder sein, da sichergestellt sein muss, dass sie positiv definit sind.[7] Positiv semidefinite Funktionen sind ebenfalls gültige Kovarianzfunktionen, wobei zu beachten ist, dass diese nicht notwendigerweise invertierbare Kovarianzmatrizen ergeben und daher meistens mit einer positiv definiten Funktion kombiniert werden.
Rechenoperationen mit Gaußprozessen
[Bearbeiten | Quelltext bearbeiten]Mit Gaußprozessen (oder Normalverteilungen) können verschiedene stochastische Rechenoperationen durchgeführt werden mit denen unterschiedliche Funktionen mit normalverteilten Fehlern miteinander in Verbindung gebracht oder aus einander extrahiert werden können. Liegen Kreuzkorrelationen zwischen den Funktionen vor, wird zusätzlich vorausgesetzt, dass sie auch im Verbund normalverteilt sind. In der Signalverarbeitung werden mit den Operationen z. B. zeitliche Signale und deren Messunsicherheiten behandelt. Die Verteilungen dieser Funktionen werden in den folgenden Operationen in der Vektor- und Matrixschreibweise für endlich viele Stützstellen dargestellt, was analog auf beliebige Erwartungswertfunktionen und Kovarianzfunktionen anwendbar ist. Die normalverteilten Vektoren (, etc.) werden entsprechend als Funktionen beschrieben.
Lineare Transformation
[Bearbeiten | Quelltext bearbeiten]Addition: unkorrelierte Funktionen
[Bearbeiten | Quelltext bearbeiten]Wird die Summe von zwei unabhängigen (und insbesondere unkorrelierten) Funktionen gebildet, dann addieren sich deren Erwartungswertfunktionen und deren Kovarianzfunktionen:
Die zugehörigen Wahrscheinlichkeitsdichtefunktionen erfahren dadurch eine Faltung.
Addition: korrelierte Funktionen
[Bearbeiten | Quelltext bearbeiten]Korrelierte Funktionen können im Extremfall identisch sein oder sich nur durch konstante Faktoren unterschieden. Die Summe entspricht dann einer Multiplikation mit den addierten Faktoren. Sind beide Funktionen identisch, ergibt sich .
Differenz: unkorrelierte Funktionen
[Bearbeiten | Quelltext bearbeiten]Wird die Differenz von zwei unabhängigen Funktionen gebildet, dann subtrahieren sich deren Erwartungswertfunktionen und es addieren sich deren Kovarianzfunktionen:
Subtraktion eines korrelierten Anteils
[Bearbeiten | Quelltext bearbeiten]Wenn die Funktion y2 einen additiven Anteil der Funktion y1 eines anderen Gaußprozesses beschreibt, dann bewirkt die Subtraktion dieses Anteils die Subtraktion der Erwartungswertfunktion und der Kovarianzfunktion:
Der Rückstrich-Operator wurde hier symbolisch verwendet im Sinne von „ohne den enthaltenen Anteil“.
Multiplikation
[Bearbeiten | Quelltext bearbeiten]Die folgende Multiplikation mit einer beliebigen Matrix enthält auch die Spezialfälle des Produkts mit einer konstanten Funktion (Diagonalmatrix ) oder mit einem Skalar ():
Hier sei darauf hingewiesen, dass ein Produkt zweier Gaußprozesse miteinander keinen weiteren Gaußprozess ergäbe, da die resultierende Wahrscheinlichkeitsverteilung die Eigenschaft der Gaußförmigkeit verloren hätte.
Allgemeine lineare Transformation
[Bearbeiten | Quelltext bearbeiten]Alle bisher gezeigten Operationen sind Spezialfälle der allgemeinen linearen Transformation:
Dieser Zusammenhang[8] beschreibt die Summe mit den konstanten Matrizen und und den Stützstellenvektoren und zweier Gaußprozesse mit und . Bei partiell korrelierten Funktionen und muss die Kreuzkovarianzmatrix gegeben sein und es wird vorausgesetzt, dass die Funktionen auch im Verbund normalverteilt sind. Die Summe ist dann zu mit der Kreuzkovarianzmatrix korreliert und zu mit .[9] Eine Kreuzkovarianzmatrix zwischen zwei Funktionen und kann mit deren Kovarianzmatrizen und in eine Kreuzkorrelationsmatrix umgerechnet werden über den Zusammenhang . Bei zwei teilkorrelierten Gaußprozessen ist zu beachten, dass spezielle Abhängigkeiten vorliegen können, bei denen die Summe keine Normalverteilung ergibt und die Gleichung dadurch ihre Gültigkeit verliert, obwohl beide Eingangsgrößen normalverteilt sind.
Fusion
[Bearbeiten | Quelltext bearbeiten]Wenn zwei verschiedene und unabhängige Gaußprozesse vorliegen, welche dieselbe gesuchte Funktion mit zueinander unkorrelierten Fehlern beschreiben, dann kann eine Vereinigung oder Fusion[10] (auch Sensordatenfusion) der beiden Teilinformationen gebildet werden, um eine Reduktion des Fehlers bzw. der Varianz zu erreichen. Beispielsweise wird in der Signalverarbeitung derselbe Kurvenverlauf mit zweierlei Sensoren gemessen (etwa die Trajektorie eines Flugzeugs durch einen Inertialsensor und unabhängig davon durch eine GNSS-Positionsbestimmung), die zwei verschiedene voneinander unabhängige Rausch- oder Fehlersignale aufaddieren. Die vereinte oder fusionierte Verteilung
der beiden Gaußprozesse entspricht dem Überlapp bzw. dem auf Eins renormierten Produkt der beiden Wahrscheinlichkeitsdichtefunktionen und beschreibt den wahrscheinlichsten Gaußprozess unter Berücksichtigung beider Teilinformationen (siehe auch Inverse Varianzgewichtung). Die Ausdrücke können so umgeformt werden,[11] dass insgesamt nur eine Matrixinversion durchgeführt werden muss:
Voraussetzung für die Gültigkeit der Formel sind Funktionenpaare mit zueinander vollständig unkorrelierten und unabhängigen Fehlern. Liegt jedoch eine partielle Korrelation vor mit der Kreuzkovarianz , dann gilt die erweiterte und verallgemeinerte Formel, die sogenannte Bar-Shalom-Campo-Fusion,[12] bei der effektiv der korrelierte Anteil vorübergehend subtrahiert und nach der Fusion wieder hinzugefügt wird:
Zerlegung
[Bearbeiten | Quelltext bearbeiten]Eine gegebene Funktion kann näherungsweise in ihre additiven Komponenten zerlegt werden, wenn die A-Priori-Verteilungen der gesamten Funktion und der Bestandteile gegeben sind. Gemäß der Additionsregel setzt sich der Gaußprozess der gesamten Funktion
aus den A-Priori-Gaußprozessen der Anteile zusammen. Die einzelnen Komponenten können dann durch die A-posteriori-Gaußprozesse
geschätzt werden, die mit den Kreuzkovarianzen
untereinander korreliert sind. Abgesehen von sehr speziellen Fällen ist diese Zerlegung mehrdeutig. Die Komponenten sind daher gekoppelte Wahrscheinlichkeitsverteilungen möglicher Lösungen um die jeweils wahrscheinlichste Lösung (siehe auch Beispiel: Signalzerlegung).
Die Zerlegung basiert auf den Gleichungen zur Fusion im vorigen Abschnitt, welche auf die speziellen Verteilungen und angewendet werden. Das Dichteprodukt bzw. der Überlapp extrahiert dabei die entsprechende Komponente.[13]
Gaußprozess-Regression
[Bearbeiten | Quelltext bearbeiten]Einleitung
[Bearbeiten | Quelltext bearbeiten]Gaußprozesse können zur Interpolation, Extrapolation oder Glättung von diskreten Messdaten einer Abbildung verwendet werden. Diese Anwendung von Gaußprozessen nennt man Gaußprozess-Regression.[14] Oft wird die Methode aus historischen Gründen besonders in der räumlichen Domäne als Kriging-Verfahren bezeichnet. Sie eignet sich insbesondere für Probleme, für die keine spezielle Modellfunktion bekannt ist. Ihre Eigenschaft als Maschinenlernverfahren ermöglicht eine automatische Modellbildung auf der Basis von Beobachtungen. Dabei erfasst ein Gaußprozess das typische Verhalten des Systems, womit die für das Problem optimale Interpolation abgeleitet werden kann. Als Ergebnis erhält man eine Wahrscheinlichkeitsverteilung von möglichen Interpolationsfunktionen sowie die Lösung mit der höchsten Wahrscheinlichkeit.
Überblick über die einzelnen Schritte
[Bearbeiten | Quelltext bearbeiten]Die Berechnung einer Gaußprozess-Regression kann durch folgende Schritte durchgeführt werden:
- A-priori-Erwartungswertfunktion: Liegt ein gleichbleibender Trend in den Messwerten vor, wird eine A-priori-Erwartungswertfunktion zum Ausgleich des Trends gebildet.
- A-priori-Kovarianzfunktion: Die Kovarianzfunktion wird nach bestimmten qualitativen Eigenschaften des Systems ausgewählt oder aus Kovarianzfunktionen unterschiedlicher Eigenschaften nach bestimmten Regeln zusammengesetzt.
- Feinabstimmung der Parameter: um quantitativ korrekte Kovarianzen zu erhalten, wird die gewählte Kovarianzfunktion auf die vorhandenen Messwerte gezielt oder durch ein Optimierungsverfahren angepasst bis die Kovarianzfunktion die empirischen Kovarianzen wiedergibt.
- Bedingte Verteilung: Durch Berücksichtigung von bekannten Messwerten wird aus dem A-priori-Gaußprozess der bedingte A-posteriori-Gaußprozess für neue Stützstellen mit noch unbekannten Werten berechnet.
- Interpretation: Aus dem A-posteriori-Gaußprozess wird schließlich die Erwartungswertfunktion als die bestmögliche Interpolation abgelesen und gegebenenfalls die Diagonale der Kovarianzfunktion als die ortsabhängige Varianz.
Schritt 1: A-priori-Erwartungswertfunktion
[Bearbeiten | Quelltext bearbeiten]Ein Gaußprozess ist durch eine Erwartungswertfunktion und eine Kovarianzfunktion vollständig definiert. Die Erwartungswertfunktion ist die A-priori-Schätzung des Regressionsproblems und beschreibt einen im Voraus bekannten Offset oder Trend der Daten. Die Funktion lässt sich oft durch ein einfaches Polynom beschreiben, das zur Kovarianzfunktion passend geschätzt werden kann, und in sehr vielen Fällen auch durch einen konstanten Mittelwert. Bei asymmetrischen nicht-gaußförmigen Verteilungen mit nur positiven Werten kann mitunter auch ein Mittelwert von Null die besten Ergebnissen liefern.
Schritt 2: A-priori-Kovarianzfunktion
[Bearbeiten | Quelltext bearbeiten]In praktischen Anwendungen muss aus endlich vielen diskreten Messwerten oder endlich vielen Beispielkurven ein Gaußprozess bestimmt werden. In Analogie zur eindimensionalen Gaußverteilung, die über den Mittelwert und die Standardabweichung diskreter Messwerte vollständig bestimmt ist, würde man zur Berechnung eines Gaußprozesses mehrere einzelne, jedoch vollständige Funktionen erwarten, um damit die Erwartungswertfunktion
und die (empirische) Kovarianzfunktion
zu berechnen.
Regressionsproblem und stationäre Kovarianz
[Bearbeiten | Quelltext bearbeiten]Meist liegt jedoch keine solche Verteilung exemplarischer Funktionen vor. Beim Regressionsproblem sind stattdessen nur diskrete Stützstellen einer einzelnen Funktion bekannt, die interpoliert oder geglättet werden soll. Auch in einem solchen Fall kann ein Gaußprozess ermittelt werden. Dazu wird anstatt dieser einen Funktion eine Schar aus vielen zueinander verschobenen Kopien der Funktion betrachtet. Diese Verteilung lässt sich nun mithilfe einer Kovarianzfunktion beschreiben. Meist kann sie als relative Funktion dieser Verschiebung durch ausgedrückt werden. Sie heißt dann stationäre Kovarianzfunktion und gilt gleichermaßen für alle Orte der Funktion und beschreibt die überall gleiche (also stationäre) Korrelation eines jeden Punktes zu seiner Nachbarschaft, sowie die Korrelation benachbarter Punkte untereinander.
Die Kovarianzfunktion wird analytisch dargestellt und heuristisch bestimmt oder in der Literatur nachgeschlagen. Die freien Parameter der analytischen Kovarianzfunktionen werden an die Messwerte angepasst. Sehr viele physikalische Systeme weisen eine ähnliche Form der stationären Kovarianzfunktion auf, so dass mit wenigen tabellierten analytischen Kovarianzfunktionen die meisten Anwendungen beschrieben werden können. So gibt es beispielsweise Kovarianzfunktionen für abstrakte Eigenschaften wie Glattheit, Rauigkeit (fehlende Differenzierbarkeit), Periodizität oder Rauschen, die nach bestimmten Vorschriften kombiniert und angepasst werden können, um die Eigenschaften der Messwerte nachzubilden.
Beispiele stationärer Kovarianz
[Bearbeiten | Quelltext bearbeiten]Die folgende Tabelle zeigt Beispiele von Kovarianzfunktionen mit solchen abstrakten Eigenschaften. Die Beispiel-Kurven sind zufällige Stichproben des jeweiligen Gaußprozesses und repräsentieren typische Kurvenverläufe. Sie wurden mit der jeweiligen Kovarianzmatrix und einem Zufallsgenerator für mehrdimensionale Normalverteilungen als korrelierter Zufallsvektor erzeugt. Die stationären Kovarianzfunktionen werden hier als eindimensionale Funktionen mit abgekürzt.
| Eigenschaft | Beispiele stationärer Kovarianzfunktionen | Zufallsfunktionen |
|---|---|---|
| Konstant | 
| |
| Glatt | 
| |
| Rau | 
| |
| Periodisch | 
| |
| Rauschen | 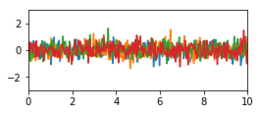
| |
| Gemischt (periodisch, glatt und verrauscht) |

|
Konstruktion neuer Kovarianzfunktionen
[Bearbeiten | Quelltext bearbeiten]Die Eigenschaften können nach bestimmten Rechenvorschriften kombiniert werden. Das grundsätzliche Ziel bei der Konstruktion einer Kovarianzfunktion ist, die wahren Kovarianzen möglichst gut wiederzugeben, während gleichzeitig die Bedingung der positiven Definitheit erfüllt wird. Die gezeigten Beispiele, außer die Konstante, besitzen letztere Eigenschaft und auch die Additionen und Multiplikationen solcher Funktionen bleiben positiv definit. Die konstante Kovarianzfunktion ist nur positiv semidefinit und muss mit mindestens einer positiv definiten Funktion kombiniert werden. Die unterste Kovarianzfunktion in der Tabelle zeigt eine mögliche Mischung verschiedener Eigenschaften. Die Funktionen in diesem Beispiel sind über eine bestimmte Distanz hinweg periodisch, weisen ein relativ glattes Verhalten auf und sind mit einem bestimmten Messrauschen überlagert.
Bei gemischten Eigenschaften gilt: [15]
- Bei additiven Effekten werden die Kovarianzen addiert, wie zum Beispiel bei der Überlagerung von Messrauschen.
- Bei sich gegenseitig verstärkenden oder abschwächenden Effekten werden die Kovarianzen multipliziert, wie zum Beispiel beim langsamen Abklingen der Periodizität.
Mehrdimensionale Funktionen
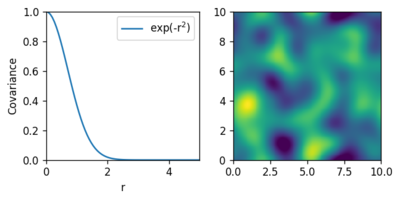
[Bearbeiten | Quelltext bearbeiten]Was hier mit eindimensionalen Funktionen gezeigt ist, lässt sich analog auch auf mehrdimensionale Systeme übertragen, indem lediglich der Abstand durch eine entsprechende n-dimensionale Abstandsnorm ersetzt wird. Die Stützpunkte in den höheren Dimensionen werden in einer beliebigen Reihenfolge abgewickelt und mit Vektoren dargestellt, so dass sie genauso wie im eindimensionalen Fall verarbeitet werden können. Die beiden folgenden Abbildungen zeigen zwei Beispiele mit zweidimensionalen Gaußprozessen und unterschiedlichen stationären und radialen Kovarianzfunktionen. In der rechten Abbildung ist jeweils eine zufällige Stichprobe des Gaußprozesses dargestellt.
Nicht-stationäre Kovarianzfunktionen
[Bearbeiten | Quelltext bearbeiten]Gaußprozesse können auch nicht-stationäre Eigenschaften der Kovarianzfunktion besitzen, also relative Kovarianzfunktionen, die sich als Funktion des Ortes ändern. In der Literatur wird beschrieben, wie nicht-stationäre Kovarianzfunktionen konstruiert werden können, so dass auch hier die positive Definitheit sichergestellt wird. Eine einfach Möglichkeit ist z. B. eine Interpolation unterschiedlicher Kovarianzfunktionen über den Ort mit der inversen Distanzwichtung.
Schritt 3: Feinabstimmung der Parameter
[Bearbeiten | Quelltext bearbeiten]Die qualitativ konstruierten Kovarianzfunktionen enthalten Parameter, sogenannte Hyperparameter, die an das System angepasst (kalibriert) werden müssen, um quantitativ korrekte Ergebnisse erzielen zu können. Dies kann durch direktes Wissen über das System erfolgen, z. B. über den bekannten Wert der Standardabweichung des Messrauschens oder die A-priori-Standardabweichung des Gesamtsystems (sigma prior, entspricht quadriert den Diagonalelementen der Kovarianzmatrix).
Die Parameter können aber auch automatisch angepasst werden. Dazu verwendet man die Randwahrscheinlichkeit, also die Wahrscheinlichkeitsdichte für eine gegebene Messkurve als ein Maß für die Übereinstimmung zwischen dem vermuteten Gaußprozess und einer vorhandenen Messkurve. Die Parameter werden dann so optimiert, dass diese Übereinstimmung maximal wird. Da die Exponentialfunktion streng monoton ist, genügt es, den Exponenten der Wahrscheinlichkeitsdichtefunktion zu maximieren, die sogenannte Log-Marginal-Likelihood-Funktion[16]
mit dem Messwert-Vektor der Länge und der von Hyperparametern abhängigen Kovarianzmatrix . Mathematisch bewirkt die Maximierung der Randwahrscheinlickeit eine optimale Abwägung zwischen der Genauigkeit (Minimierung der Residuen) und der Einfachheit der Theorie. Eine einfache Theorie zeichnet sich durch große Nebendiagonalelemente aus, wodurch eine hohe Korrelation im System beschrieben wird. Das bedeutet, dass wenige Freiheitsgrade im System vorhanden sind und somit die Theorie in gewisser Weise mit wenigen Regeln auskommt, um alle Zusammenhänge zu erklären. Sind diese Regeln zu einfach gewählt, würden die Messungen nicht hinreichend gut wiedergegeben werden und die residuellen Fehler wachsen zu stark an. Bei einer maximalen Randwahrscheinlichkeit ist das Gleichgewicht einer optimalen Theorie gefunden, sofern hinreichend viele Messdaten für eine gute Konditionierung zur Verfügung standen. Diese implizite Eigenschaft der Maximum-Likelihood-Methode kann auch als Ockhams Sparsamkeitsprinzip verstanden werden.[17]
Schritt 4: Bedingter Gaußprozess bei bekannten Stützpunkten
[Bearbeiten | Quelltext bearbeiten]Ist der Gaußprozess eines Systems wie oben bestimmt worden, sind also Erwartungswertfunktion und Kovarianzfunktion bekannt, kann mit dem Gaußprozess eine Vorhersage beliebiger interpolierter Zwischenwerte berechnet werden, wenn nur wenige Stützstellen der gesuchten Funktion durch Messwerte bekannt sind. Die Vorhersage erfolgt durch die bedingte Wahrscheinlichkeit einer mehrdimensionalen Gaußverteilung bei einer gegebenen Teilinformation. Die Dimensionen der mehrdimensionalen Gaußverteilung
werden dabei unterteilt in unbekannte Werte, die vorhergesagt werden sollen (Index U für unbekannt) und in bekannte Messwerte (Index B für bekannt). Vektoren zerfallen dadurch in zwei Teile. Die Kovarianzmatrix wird entsprechend in vier Blöcke unterteilt: Kovarianzen innerhalb der unbekannten Werte (UU), innerhalb der bekannten Messwerte (BB) und Kovarianzen zwischen den unbekannten und bekannten Werten (UB und BU). Die Werte der Kovarianzmatrix werden an diskreten Stellen der Kovarianzfunktion abgelesen und der Erwartungswertvektor an entsprechenden Stellen der Erwartungswertfunktion: bzw.
Durch die Berücksichtigung der bekannten Messwerte verändert sich die Verteilung zur bedingten bzw. A-posteriori-Normalverteilung
- ,
wobei die gesuchten unbekannten Variablen sind. Die Notation bedeutet „bedingt durch “.
Der erste Parameter der resultierenden Gaußverteilung beschreibt den neuen gesuchten Erwartungswertvektor, der jetzt den wahrscheinlichsten Funktionswerten der Interpolation entspricht. Zusätzlich wird im zweiten Parameter die vollständige vorhergesagte neue Kovarianzmatrix gegeben. Diese enthält insbesondere die Vertrauensintervalle der vorhergesagten Erwartungswerte, gegeben durch die Wurzel der Hauptdiagonalelemente.
Messrauschen und andere Störsignale
[Bearbeiten | Quelltext bearbeiten]Weißes Messrauschen der Varianz kann als Teil des A-Priori-Kovarianzmodells modelliert werden, indem der Diagonale von entsprechende Terme hinzugefügt werden. Wird mit derselben Kovarianzfunktion auch die Matrix gebildet, würden auch die vorhergesagte Verteilung ein weißes Rauschen der Varianz beschreiben. Um eine Vorhersage eines unverrauschten Signals zu erhalten, werden in der A-posteriori-Verteilung
bei und gegebenenfalls in und die entsprechenden Terme weggelassen. Dadurch wird das Messrauschen so gut wie möglich weggemittelt, was auch im vorhergesagten Vertrauensintervall korrekt berücksichtigt wird. Auf die gleiche Weise kann jegliches unerwünschte additive Störsignal von den Messdaten entfernt werden (siehe auch Rechenoperation Zerlegung), sofern es sich mit einer Kovarianzfunktion beschreiben lässt und sich vom Nutzsignal hinreichend gut unterscheidet. Dazu wird anstelle der Diagonalmatrix die entsprechende Kovarianzmatrix der Störung eingesetzt. Messungen mit Störsignalen benötigen also zwei Kovarianzmodelle: für das zu schätzende Nutzsignal und für das Rohsignal.
Herleitung der bedingten Verteilung
[Bearbeiten | Quelltext bearbeiten]Die Herleitung kann über die Bayes-Formel erfolgen, indem die beiden Wahrscheinlichkeitsdichten für bekannte und unbekannte Stützstellen sowie die Verbundwahrscheinlichkeitsdichte eingesetzt werden. Die resultierende bedingte A-posteriori-Normalverteilung entspricht dem Überlapp oder Schnittbild der Gaußverteilung mit dem durch die bekannten Werte aufgespannten Untervektorraum.
Bei verrauschten Messwerten, die selbst eine mehrdimensionale Normalverteilung darstellen, erhält man den Überlapp zur A-Priori-Verteilung durch die Multiplikation der beiden Wahrscheinlichkeitsdichten. Das Produkt der Wahrscheinlichkeitsdichten zweier mehrdimensionaler Normalverteilungen entspricht der Rechenoperationen Fusion, mit der die Verteilung bei unterdrücktem Störsignal hergeleitet werden kann.
A-posteriori Gaußprozess
[Bearbeiten | Quelltext bearbeiten]In der vollständigen Darstellung als Gaußprozess ergibt sich aus dem A-priori-Gaußprozess
und den bekannten Messwerten an den Koordinaten eine neue Verteilung, gegeben durch den bedingten A-posteriori-Gaußprozess
mit
- .
ist dabei eine Kovarianzmatrix, die sich durch die Auswertung der Kovarianzfunktion an den diskreten Zeilen und Spalten ergibt. Außerdem wurde entsprechend als Vektor von Funktionen gebildet, indem nur an diskreten Zeilen oder diskreten Spalten ausgewertet wurde.
In praktischen numerischen Berechnungen mit endlichen Zahlen von Stützstellen wird nur mit der Gleichung der bedingten mehrdimensionalen Normalverteilung gearbeitet. Die Notation des A-posteriori-Gaußprozesses dient hier nur dem theoretischen Verständnis, um den Grenzwert zum Kontinuum in Form von Funktionen zu beschreiben und damit die Zuordnung der Werte zu den Koordinaten darzustellen.
Schritt 5: Interpretation
[Bearbeiten | Quelltext bearbeiten]Aus dem A-priori-Gaußprozess erhält man mit den Messwerten einen A-posteriori-Gaußprozess, der die bekannte Teilinformation berücksichtigt. Dieses Ergebnis der Gaußprozess-Regression repräsentiert nicht nur eine Lösung, sondern die Gesamtheit aller möglichen und mit unterschiedlichen Wahrscheinlichkeiten gewichteten Lösungsfunktionen der Interpolation. Die damit ausgedrückte Unentschiedenheit ist keine Schwäche der Methode. Sie wird dem Problem genau gerecht, da bei einer nicht vollständig bekannten Theorie oder bei verrauschten Messwerten die Lösung prinzipiell nicht eindeutig bestimmbar ist. Meist interessiert man sich jedoch speziell für diejenige Lösung mit der zumindest höchsten Wahrscheinlichkeit. Diese ist durch die Erwartungswertfunktion im ersten Parameter des A-posteriori-Gaußprozesses gegeben. Aus der bedingten Kovarianzfunktion im zweiten Parameter lässt sich die Streuung um diese Lösung ablesen. Die Diagonale der Kovarianzfunktion gibt eine Funktion mit den Varianzen der vorhergesagten wahrscheinlichsten Funktion wieder. Das Vertrauensintervall ist dann durch die Grenzen gegeben.
Beispiele
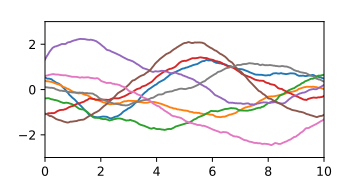
[Bearbeiten | Quelltext bearbeiten]- A-priori- und A-posteriori-Gaußprozesse
-
A-priori-Gaußprozess, dargestellt durch damit erzeugte Zufallskurven.
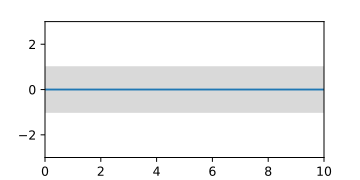
-
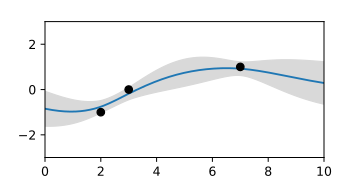
A-priori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und die Fläche des Vertrauensintervalls.
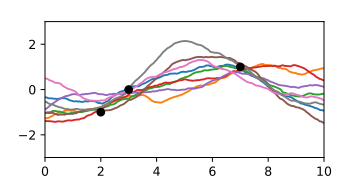
-
A-posteriori-Gaußprozess bei Kenntnis von drei Stützpunkten, dargestellt durch Zufallskurven.
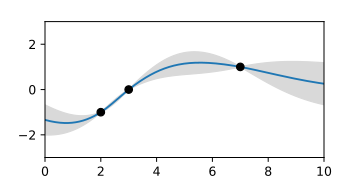
-
A-posteriori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls.
-
A-posteriori-Gaußprozess bei angenommenem Messrauschen. Die Interpolationen treffen die Punkte nicht mehr exakt.
-
A-posteriori-Gaußprozess bei angenommenem Messrauschen. Der Erwartungswert wird glatter und das Vertrauensintervall bleibt größer Null.
-
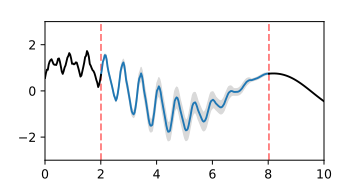
A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls
-
A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch animierte Zufallsfluktuationen gemäß der Verteilung.
Der Python-Code der Beispiele findet sich auf der jeweiligen Bildbeschreibungsseite.
Sonderfälle
[Bearbeiten | Quelltext bearbeiten]Unterbestimmte Messwerte
[Bearbeiten | Quelltext bearbeiten]In manchen Fällen von bedingten Gaußprozessen sind Gruppen von linear zusammenhängenden Messwerten vollständig unbestimmt, z. B. bei indirekten Messwerten, die aus unterbestimmten Gleichungen folgen, etwa mit einer nicht invertierbaren positiv semidefiniten Matrix der Form . Die Stützstellen lassen sich dann nicht einfach in bekannte und unbekannte Werte aufteilen und die zugehörige Kovarianzmatrix wäre aufgrund unendlicher Unsicherheiten singulär. Das entspräche einer Normalverteilung, die in bestimmte Raumrichtungen quer zu den Koordinatenachsen unendlich ausgedehnt ist. Um die Beziehungen zwischen den unbestimmten Variablen zu berücksichtigen, muss in einem solchen Fall mit der inversen Matrix , der sogenannten Präzisionsmatrix, gerechnet werden. Diese kann vollständig unbestimmte Messwerte beschreiben, was durch Nullen in der Diagonale ausgedrückt wird. Für eine solche singuläre Verteilung mit teilweise unbekannten Messwerten und singulären Messunsicherheiten wird die gesuchte A-posteriori-Verteilung durch den Überlapp zum A-priori-Gaußprozess-Modell berechnet, indem die Wahrscheinlichkeitsdichten multipliziert werden. Die Vereinigung der beiden Normalverteilungen
erhält man durch die Operation Fusion nach Umformung, so dass die singuläre der beiden Matrizen invers bleibt. Im Ergebnis ergibt sich immer eine endliche Verteilung, da die endliche Matrix dominiert. Sind beide endlich, lässt sich die Gleichung in die Form des A-posteriori-Gaußprozesses bringen wie im Abschnitt zur bedingten Verteilung.
Linearkombination zu einem Gaußprozess
[Bearbeiten | Quelltext bearbeiten]Aus gegebenen Basisfunktionen soll eine Linearkombination gebildet werden, die mit der Verteilung eines zugehörigen Gaußprozesses maximalen Überlapp hat. Oder es sollen Messwerte approximiert werden, während das darin enthaltene Störsignal möglichst ignoriert wird. In beiden Fällen können die gesuchten Koeffizienten mit der verallgemeinerten Kleinste-Quadrate-Schätzung
berechnet werden. Dabei enthält die Matrix die Funktionswerte der Basisfunktionen an den Stützstellen . Die resultierenden Koeffizienten c mit der zugehörigen Kovarianzmatrix beschreiben diejenige Linearkombination mit der größtmöglichen Wahrscheinlichkeitsdichte in der Verteilung . Die Linearkombination approximiert dabei die Erwartungswertfunktion oder die Messwerte auf eine solche Weise, dass die Residuen bestmöglich durch die Kovarianzmatrix beschrieben werden. Die Methode wird beispielsweise in der Programmbibliothek Scikit-learn genutzt, um eine polynomiale Erwartungswertfunktion eines Gaußprozesses empirisch zu schätzen.
Approximation eines empirischen Gaußprozesses
[Bearbeiten | Quelltext bearbeiten]Ein aus Beispielfunktionen empirisch bestimmter Gaußprozess
mit wenigen stark ausgeprägten Freiheitsgraden kann mittels einer Eigenwertzerlegung oder der Singulärwertzerlegung
der Kovarianzmatrix approximiert und vereinfacht werden. Dazu wählt man die größten Eigenwerte bzw. Singulärwerte aus der Diagonalmatrix . Die zugehörigen Spalten von sind die Hauptkomponenten des Gaußprozesses (siehe Hauptkomponentenanalyse). Stellt man die Spalten als Funktionen dar, dann wird der ursprüngliche Gaußprozess durch die Mittelwertfunktion und die Kovarianzfunktion
approximiert. Dieser Gaußprozess beschreibt ausschließlich Funktionen der Linearkombination
- ,
wobei jeder Koeffizient als unabhängige Zufallsvariable der Varianz um den Mittelwert Null gestreut wird.
Eine solche Vereinfachung ist positiv semidefinit und ihr fehlen meist die Eigenschaften zur Beschreibung kleinskaliger Variationen. Diese Eigenschaften können der Kovarianzfunktion in Form einer an die Residuen angepassten stationären Kovarianzfunktion hinzugefügt werden:
Gaußprozesse mit linearen Nebenbedingungen
[Bearbeiten | Quelltext bearbeiten]Im Falle vieler interessanter Anwendungen ist bereits im Vorhinein Wissen über das Verhalten des betrachteten Systems vorhanden. Man betrachte zum Beispiel den Fall, in dem der Gaußprozess ein Magnetfeld beschreiben soll; hier gehorcht dann das echte Magnetfeld den Maxwell-Gleichungen und es wäre vorteilhaft, dieses Wissen auch in den Gaußprozess zu inkludieren, da dies höchstwahrscheinlich dessen Vorhersagekraft verbessern würde.
Es gibt bereits eine Methode, um lineare Nebenbedingungen in den Formalismus des Gaußprozesses miteinzubeziehen:[18]
Betrachte die (vektorwertige) Funktion , die bekanntermaßen der linearen Nebenbedingung (d. h. ist ein linearer Operator)
gehorcht. Dann kann die Nebenbedingung erfüllt werden, indem man wählt (wobei es sich bei um einen Gaußprozess handelt) und anschließend bestimmt, sodass
Mit gegebenem und unter Verwendung der Tatsache, dass Gaußprozesse abgeschlossen unter linearen Transformationen sind, kann der Gaußprozess für , der der Nebenbedingung gehorcht, geschrieben werden als
Somit können lineare Nebenbedingungen im Mittelwert und der Kovarianzfunktion des Gaußprozesses berücksichtigt werden.
Anwendungsbeispiele
[Bearbeiten | Quelltext bearbeiten]Beispiel: Trend-Vorhersage
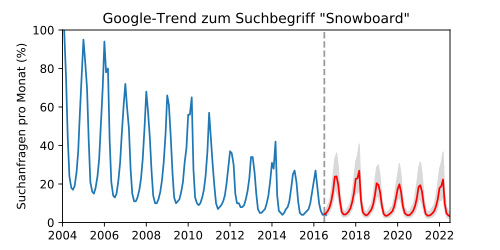
[Bearbeiten | Quelltext bearbeiten]In einem hypothetischen Anwendungsbeispiel aus der Marktforschung soll die zukünftige Nachfrage zum Thema „Snowboard“ vorhergesagt werden. Dazu soll eine Extrapolation der Anzahl von Google-Suchanfragen[19] zu diesem Begriff berechnet werden.
In den vergangenen Daten erkennt man eine periodische, jedoch nicht sinusförmige Jahreszeitabhängigkeit, die durch den Winter auf der Nordhalbkugel zu erklären ist. Außerdem nahm der Trend über das letzte Jahrzehnt kontinuierlich ab. Zusätzlich erkennt man eine wiederkehrende Erhöhung der Suchanfragen während der olympischen Spiele alle vier Jahre. Die Kovarianzfunktion wurde daher mit einem langsamen Trend sowie einer ein- und vierjährigen Periode modelliert:
Der Trend scheint außerdem eine deutliche Asymmetrie aufzuweisen. Das kann der Fall sein, wenn sich die zugrundeliegenden Zufallseffekte nicht addieren, sondern gegenseitig verstärken, was eine Log-Normal-Verteilung zur Folge hat. Der Logarithmus solcher Werte beschreibt jedoch eine Normalverteilung, worauf die Gaußprozess-Regression angewendet werden kann.
Die Abbildung zeigt eine Extrapolation der Kurve (rechts der gestrichelten Linie). Da die Ergebnisse hier mit einer Exponentialfunktion aus der logarithmischen Darstellung zurücktransformiert wurden, sind die vorhergesagten Vertrauensintervalle entsprechend asymmetrisch (graue Fläche). Die Extrapolation zeigt plausibel die saisonalen Verläufe und auch die Erhöhung der Suchanfragen bei den Olympischen Spielen alle vier Jahre. Das Beispiel mit gemischten Eigenschaften demonstriert sehr gut die vielfältigen Modellierungsmöglichkeiten der Gaußprozess-Regression, die in einem Interpolationsverfahren vereinheitlicht sind.
Python Quellcode der Beispielrechnung
Beispiel: Sensorkalibrierung
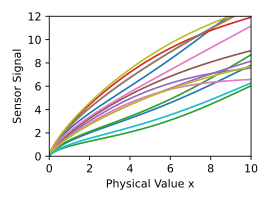
[Bearbeiten | Quelltext bearbeiten]In einem Anwendungsbeispiel aus der Industrie sollen mithilfe von Gaußprozessen Sensoren kalibriert werden.[20][21] Aufgrund von Toleranzen bei der Herstellung zeigen die Kennlinien der Sensoren große individuelle Unterschiede. Das verursacht hohe Kosten bei der Kalibrierung, da für jeden Sensor eine vollständige Kennlinie gemessen werden müsste. Der Aufwand kann jedoch minimiert werden, indem das genaue Verhalten der Streuung durch einen Gaußprozess erlernt wird. Dazu werden von zufällig ausgewählten repräsentativen Sensoren die vollständigen Kennlinien gemessen und damit der Gaußprozess der Streuung durch
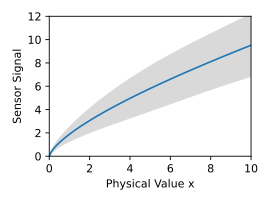
berechnet. Im gezeigten Beispiel sind 15 repräsentative Kennlinien gegeben. Der daraus resultierende Gaußprozess ist durch die Mittelwertfunktion und das Vertrauensintervall dargestellt.
Mit dem bedingten Gaußprozess mit
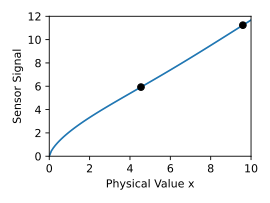
kann nun für jeden neuen Sensor mit wenigen einzelnen Messwerten an den Koordinaten das vollständige Kennfeld rekonstruiert werden. Die Anzahl von Messwerten muss dabei mindestens der Anzahl der Freiheitsgrade der Toleranzen entsprechen, die einen unabhängigen linearen Einfluss auf die Form der Kennlinie haben.
Im dargestellten Beispiel genügt ein einzelner Messwert noch nicht, um die Kennlinie eindeutig und präzise zu bestimmen. Das Vertrauensintervall zeigt den Bereich der Kurve, der noch nicht ausreichend genau ist. Mit einem weiteren Messwert in diesem Bereich kann schließlich die verbleibende Unsicherheit vollständig eliminiert werden. Die Exemplarschwankungen der sehr unterschiedlich wirkenden Sensoren in diesem Beispiel scheinen also durch die Toleranzen von nur zwei relevanten inneren Freiheitsgraden verursacht zu werden.
Python Quellcode der Beispielrechnung
Beispiel: Signalzerlegung
[Bearbeiten | Quelltext bearbeiten]In einem Anwendungsbeispiel für die Signalverarbeitung soll ein zeitliches Signal in seine Bestandteile zerlegt werden. Über das System sei bekannt, dass das Signal aus drei Komponenten besteht, die den drei Kovarianzfunktionen
folgen. Das Summensignal folgt dann nach der Additionsregel der Kovarianzfunktion
- .
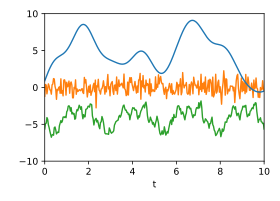
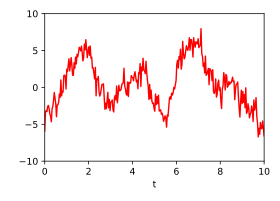
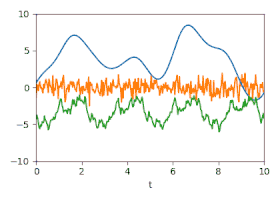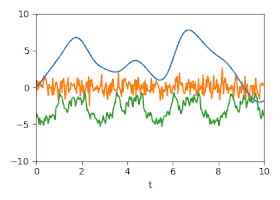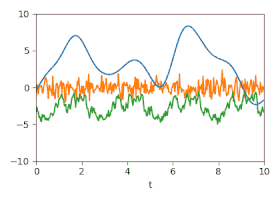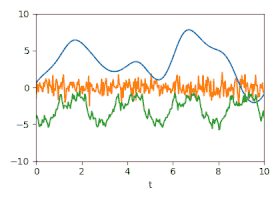
Die folgenden beiden Abbildungen zeigen drei Zufallssignale, die zur Demonstration mit diesen Kovarianzfunktionen erzeugt und addiert wurden. In der Summe der Signale kann man mit bloßem Auge kaum das darin verborgene periodische Signal erkennen, da dessen Spektralbereich mit dem der beiden anderen Komponenten überlappt.
-
Einzelsignale: Drei zufällig erzeugte Signale, die bestimmten Gaußprozessen folgen.
-
Summe: Die Summe der drei Signale.
Mithilfe der Operation Zerlegung kann die Summe wieder in die drei Komponenten
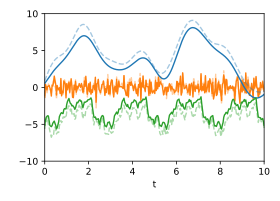
zerlegt werden, wobei . Die Schätzung der wahrscheinlichsten Zerlegung zeigt, wie gut die Trennung in diesem Fall möglich ist und wie nah die Signale an den ursprünglichen Signalen liegen. Die geschätzten Unsicherheiten unter Berücksichtigung der Kreuzkorrelationen sind in der Animation durch Zufallsfluktuationen dargestellt.
-
Zerlegung: Wahrscheinlichste Zerlegung bei Kenntnis der jeweiligen Kovarianzfunktionen. Die ursprünglichen Signale sind gestrichelt dargestellt.
-
Unsicherheit: Geschätzte Unsicherheiten dargestellt durch animierte Zufallsfluktuationen entsprechend der (Kreuz-)Kovarianzmatrizen.
Das Beispiel zeigt, wie mit diesem Verfahren sehr verschiedenartige Signale in einem Schritt getrennt werden können. Andere Filterverfahren wie gleitende Mittelung, Fourierfilterung, Polynomregression oder Splineapproximation sind dagegen auf spezielle Signaleigenschaften optimiert und liefern weder genaue Fehlerschätzungen noch Kreuzkorrelationen.
Sind die Gaußprozesse der Einzelkomponenten für ein gegebenes Signal nicht genau bekannt, dann kann in manchen Fällen eine Hypothesenprüfung mithilfe der Log-Marginal-Likelihood-Funktion durchgeführt werden, sofern hinreichend viele Daten für eine gute Konditionierung der Funktion zur Verfügung stehen. Über deren Maximierung können die Parameter der vermuteten Kovarianzfunktionen an die Messdaten angepasst werden.
Python Quellcode der Beispielrechnung
Literatur
[Bearbeiten | Quelltext bearbeiten]- C. E. Rasmussen: Gaussian Processes in Machine Learning. In: Olivier Bousquet (Hrsg.): Advanced Lectures on Machine Learning. ML 2003. (= Lecture Notes in Computer Science. vol. 3176). Springer, Berlin/Heidelberg 2004. doi:10.1007/978-3-540-28650-9_4 (cs.ubc.ca, pdf)
- C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning. MIT Press, 2006, ISBN 0-262-18253-X. (gaussianprocess.org, pdf)
- R. M. Dudley: Real Analysis and Probability. Wadsworth and Brooks/Cole, 1989.
- B. Simon: Functional Integration and Quantum Physics. Academic Press, 1979.
- M. L. Stein: Interpolation of Spatial Data: Some Theory for Kriging. Springer, 1999.
Weblinks
[Bearbeiten | Quelltext bearbeiten]Lehrmaterial
[Bearbeiten | Quelltext bearbeiten]- Gaussian Processes Web Site (Lehrbuch, Tutorials, Code etc.)
- Interaktive Demo zur Gaußprozess-Regression
- The Kernel Cookbook (Anleitung zur Konstruktion von Kovarianzfunktionen)
Software
[Bearbeiten | Quelltext bearbeiten]- GPy – Ein Gaussian processes Framework in Python
- Scikit Learn Gaussian Process – Gaußprozess-Modul der Maschinenlern-Bibliothek Scikit-learn für Python
- ooDACE – Eine flexible Matlab Toolbox.
- GPstuff – Gaussian process toolbox for Matlab and Octave
- Gaussian process Library geschrieben in C++11
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Motonobu Kanagawa, Philipp Hennig, Dino Sejdinovic, Bharath K Sriperumbudur: Gaussian Processes and Kernel Methods: A Review on Connections and Equivalences. 2018, doi:10.48550/ARXIV.1807.02582.
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning, Chapter 4.1 Preliminaries
- ↑ Topics in Probability: Gaussian Analysis, Math 7880-1, Spring 2015, University of Utah, Chapter 6 "Gaussian Processes", siehe Definition 1.7 für Stationarität und Lemma 1.8 zur Translationsinvarianz.
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning. MIT Press, 2006, ISBN 0-262-18253-X, Kapitel 4.2 Examples of Covariance Functions, Seite 85
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning. MIT Press, 2006, ISBN 0-262-18253-X, Kapitel 4.2 Examples of Covariance Functions, Seite 84.
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning MIT Press, 2006, ISBN 0-262-18253-X, Kapitel 4.2.2 Dot Product Covariance Functions. S. 89 und Table 4.1, S. 94.
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning. MIT Press, 2006, ISBN 0-262-18253-X, Kapitel 4 Covariance Functions, valide Kovarianzfunktionen sind zum Beispiel in Table 4.1 auf Seite 94 als ND aufgelistet.
- ↑ Die Herleitung der allgemeinen linearen Transformation erfolgt aus der Gleichung , indem die Matrix F als [A B] gewählt wird, als Vektor ( ) und aus entsprechenden vier Blöcken.
- ↑ Die Herleitung erfolgt mit der Kovarianz-Regel für Multiplikation und Assoziativität .
- ↑ Benjamin Noack, Joris Sijs, Uwe D. Hanebeck: Fusion Strategies for Unequal State Vectors in Distributed Kalman Filtering. In: IFAC Proceedings Volumes (= 19th IFAC World Congress). Band 47, Nr. 3, 1. Januar 2014, ISSN 1474-6670, S. 3262–3267, doi:10.3182/20140824-6-ZA-1003.02491 (sciencedirect.com).
- ↑ Bei der Umformung wird z. B. mit 1 = Σ1/Σ1 multipliziert oder 0 = Σ1-Σ1 addiert und die inversen Matrizen entsprechend gekürzt.
- ↑ Yaakov Bar-Shalom, Leon Campo: The Effect of the Common Process Noise on the Two-Sensor Fused-Track Covariance. In: IEEE Transactions on Aerospace and Electronic Systems. AES-22, Nr. 6, November 1986, ISSN 0018-9251, S. 803–805, doi:10.1109/TAES.1986.310815 (ieee.org).
- ↑ Die Strategie entspricht dem A-posteriori-Gaußprozess mit Messunsicherheiten, siehe Kapitel zur Gaußprozess-Regression im Lehrbuch C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning, Chapter 2 Regression. Auch der Kalman-Filter nutzt die Datenfusion zur Trennung von Signalen und Messunsicherheiten.
- ↑ Als Referenz für das Kapitel "Gaußprozess-Regression" dient im Wesentlichen das Lehrbuch C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning, Chapter 2 Regression
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning, Kapitel 4.2.4 Making New Kernels from Old. S. 94.
- ↑ C. E. Rasmussen, C. K. I. Williams: Gaussian Processes for Machine Learning, Kapitel 5.2 Bayesian Model Selection. S. 108.
- ↑ Siehe "occam’s razor" im Lehrbuch Rasmussen Seite 110.
- ↑ Carl Jidling, Niklas Wahlström, Adrian Wills, Thomas B. Schön: Linearly constrained Gaussian processes. In: arXiv:1703.00787 [stat]. 19. September 2017, arxiv:1703.00787.
- ↑ Die Daten sind erhältlich bei Google-Trends zum Suchbegriff „Snowboard“.
- ↑ Mit stationären Gaußprozessen: Tao Chen u. a.: Calibration of Spectroscopic Sensors with Gaussian Process and Variable Selection. IFAC Proceedings Volumes (2007), Volume 40, Nr. 5, doi:10.3182/20070606-3-MX-2915.00141
- ↑ R. Honicky: Automatic calibration of sensor-phones using gaussian processes. EECS Department, UC Berkeley, Tech. Rep. UCB/EECS-2007-34 (2007), (eecs.berkeley.edu, pdf)









![{\displaystyle k(t,t'):=\operatorname {Cov} (X_{t},X_{t'}):=\mathbb {E} \left[(X_{t}-m(t))\cdot (X_{t'}-m(t'))\right],\quad t,t'\in T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aa08ac5d45b1abae6327583cdf7187d367347ff)


















































































![{\displaystyle \left[C_{XY}\right]_{ij}=\left[\Sigma _{XY}\right]_{ij}/{\sqrt {\left[\Sigma _{X}\right]_{ii}\left[\Sigma _{Y}\right]_{jj}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73b807ad37e251fcadcf48033cfbb3335bf26414)


















![{\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(t)-m(t)\right]\cdot \left[f_{i}(t')-m(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96ecfed304ea5479c8616aafa1a8ace01e1606c2)























![{\displaystyle X_{\text{U}}\mid X_{\text{B}}\sim {\mathcal {N}}\left(\mu _{\text{U}}+\Sigma _{\text{UB}}\left[\Sigma _{\text{BB}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}(X_{\text{B}}-\mu _{\text{B}}),\Sigma _{\text{UU}}-\Sigma _{\text{UB}}\left[\Sigma _{\text{BB}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}\Sigma _{\text{BU}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44afb367c375545bb2658019ad762484746c62b1)






































![{\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{p=1}^{N}\left[f_{p}(t)-m(t)\right]\cdot \left[f_{p}(t')-m(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f23777e5161267eaf143c21be846f58c2e93399)
























![{\displaystyle k(x,x')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(x)-m(x)\right]\cdot \left[f_{i}(x')-m(x')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/113d714d79833fc992f5e4342a985b43f7c40a4e)