Blockverschlüsselung
Eine Blockverschlüsselung (auch Blockchiffre oder auf Englisch block cipher genannt) ist ein deterministisches Verschlüsselungsverfahren, das einen Klartextblock, d. h. einen Klartextabschnitt fester Länge, auf einen Geheimtext- oder Schlüsseltextblock fester (in der Regel der gleichen) Länge abbildet. Diese Abbildung wird dabei durch einen Schlüssel beeinflusst. Kennt man diesen, kann man aus dem Geheimtext wieder den Klartext berechnen, mit etwa dem gleichen Aufwand wie für das Verschlüsseln. Ohne Kenntnis des Schlüssels ist dies hingegen viel schwieriger, bei vielen modernen Blockchiffren ist dafür keine praktikable Methode bekannt.
Im Gegensatz zu einer Stromchiffre kann eine Blockchiffre nur einen Block der gegebenen Länge verschlüsseln, wobei die Blocklänge typischerweise 64 Bit bis 256 Bit beträgt. Längere Texte werden auf ein Vielfaches der Blocklänge aufgefüllt und in Blöcke geteilt, und es wird ein Betriebsmodus gewählt, der festlegt, wie die Blockchiffre darauf anzuwenden ist.
Blockchiffren werden auch als Bausteine zur Konstruktion weiterer kryptografischer Verfahren, z. B. kryptographischer Hashfunktionen, eingesetzt.
Anforderungen
[Bearbeiten | Quelltext bearbeiten]Eine Blockchiffre soll vielen Angriffsszenarien widerstehen. Wenn etwa ein Angreifer beliebig viele mit dem gleichen Schlüssel erzeugte Paare von Klar- und Geheimtextblöcken vorliegen hat, soll es ihm dennoch nicht möglich sein, den Schlüssel zu ermitteln oder auf anderem Weg einen weiteren mit diesem Schlüssel erzeugten Geheimtext zu entziffern. Dies soll sogar dann noch gelten, wenn der Angreifer die Klartextblöcke frei wählen kann, also zu jedem von ihm konstruierten Block den unter dem gegebenen Schlüssel zugehörigen Geheimtextblock erfahren kann. Auch dann, wenn der Angreifer wahlweise einen Klar- oder Geheimtextblock frei wählen kann, soll es ihm unmöglich sein, den Schlüssel herauszufinden.
Dabei geht man davon aus, dass der Angreifer den internen Aufbau der Verschlüsselung kennt. Der Schutz der Daten soll nicht von der Geheimhaltung des Verfahrens, sondern nur von der Geheimhaltung des Schlüssels abhängen (Kerckhoffs’ Prinzip).
Weder die Blockgröße noch die Schlüssellänge darf zu klein sein. Eine Blockgröße von 64 bit, die bei älteren Blockchiffren verbreitet ist, ist bereits grenzwertig. Wenn es zu wenig mögliche Blockwerte gibt (hier ), dann ist ein Codebuchangriff möglich. Ein Angreifer sammelt möglichst viele Paare von Klar- und Schlüsseltextblöcken für einen bestimmten Schlüssel, und wenn einer dieser Schlüsseltextblöcke in irgendeiner Nachricht auftaucht (und der Schlüssel nicht inzwischen geändert wurde), kennt er damit auch den Klartextblock. Ist andererseits der Schlüssel zu klein, dann ist das Durchprobieren aller möglichen Schlüssel praktikabel, um den richtigen zu finden. Moderne Verfahren verwenden mindestens 128 bit als Block- wie auch als Schlüssellänge.
Geschichte
[Bearbeiten | Quelltext bearbeiten]Lucifer gilt als die erste zivil nutzbare Blockchiffre, sie wurde im Jahr 1971 von IBM auf der Grundlage von Horst Feistels kryptographischen Arbeiten entwickelt. Eine revidierte Version von Lucifer wurde vom National Bureau of Standards (NBS) der USA (woraus 1988 das National Institute of Standards and Technology, NIST hervorging) übernommen und zum DES (Data Encryption Standard) erklärt, nachdem Änderungen vom NBS selbst und vom Geheimdienst NSA am Algorithmus vorgenommen worden waren. Der DES wurde 1976 der Öffentlichkeit vorgestellt und fand eine weit verbreitete Anwendung. Die Blockgröße des DES ist 64 Bit und die Schlüssellänge 56 Bit.
Bereits Ende der 90er Jahre konnte DES aufgrund seiner geringen Schlüssellänge durch Brute-Force-Angriffe gebrochen werden (siehe EFF DES Cracker). Für eine Übergangszeit nutzte man deshalb Modifikationen des DES, wie etwa Triple-DES. Im Jahr 2001 wurde der DES nach einer fünfjährigen Ausschreibungsphase durch den AES (Advanced Encryption Standard) ersetzt. Der Auswahlprozess des AES wird weltweit von vielen Kryptographen wegen seiner offenen Gestaltung als vorbildlich angesehen. Der Algorithmus des AES war von Joan Daemen und Vincent Rijmen unter dem Namen Rijndael entwickelt worden. Die Blockgröße beträgt 128 Bit und die Schlüssellänge 128, 192 oder 256 Bit, vom Anwender wählbar.
Mathematische Beschreibung
[Bearbeiten | Quelltext bearbeiten]Eine Blockchiffre ist eine Funktion
- ,
die einen Klartextblock auf einen Geheimtextblock abbildet, mit dem Schlüssel als Parameter. Für jeden möglichen Schlüssel muss die Verschlüsselungsfunktion injektiv sein, da genau dann eine Entschlüsselungsfunktion existiert, die zu jedem Geheimtext wieder den Klartext berechnet:
- .
Dies ist gleichbedeutend zu der Aussage, dass die Entschlüsselungsfunktion linksinvers zur Verschlüsselungsfunktion ist.
Meist ist , und die Ver- und Entschlüsselungsfunktionen sind dann für jeden Schlüssel aus S bijektiv. Heute verwendet man außerdem fast ausschließlich Bitblockchiffren, die auf Blöcken mit b Bit arbeiten: . Die Blockgröße beträgt meist 64 oder 128 Bit, aber größere Werte kommen ebenfalls vor (z. B. Threefish; bis 1024 Bit).
Eine Blockchiffre heißt involutorisch, wenn Ver- und Entschlüsselung identisch sind, also wenn gilt:
- .
Eine bijektive Abbildung von auf ist eine Permutation von Elementen. Es gibt folglich eine extrem große Zahl () verschiedener Abbildungen (siehe Fakultät).
Durch den Schlüssel einer Blockchiffre wird von den möglichen bijektiven Abbildungen genau eine ausgewählt. Da die Schlüssellänge typischer Blockchiffren weit geringer als Bits ist, wird durch die Gesamtheit aller Schlüssel nur ein kleiner Teil aller möglichen Abbildungen erfasst. Bereits bei einer Blockgröße von nur 8 Bit wäre ein 1684 Bit langer Schlüssel nötig, um alle Permutationen zu realisieren.
Entwurfsprinzipien
[Bearbeiten | Quelltext bearbeiten]Für die interne Verarbeitung der Blockdaten gibt es zwei Ziele: Durch Konfusion soll der Zusammenhang zwischen Geheim- und Klartext so komplex und undurchschaubar wie möglich gemacht werden. Diffusion soll die Information an einer Stelle des Klartextblocks über den gesamten Geheimtextblock verteilen; am Ende soll jedes Bit des Geheimtextblocks von jedem Bit des Klartextblocks und des Schlüssels abhängen. Wenn an diesen etwas geändert wird, soll sich jedes Geheimtextbit mit der Wahrscheinlichkeit 1/2 ändern. Es sollen keine Muster erkennbar sein, mit denen man aus einem Geheimtext irgendwelche Informationen über den Klartext oder den Schlüssel gewinnen könnte.
Alle modernen Blockchiffren wie AES oder DES sind als iterierte Blockchiffren konzipiert. Das bedeutet, dass die Eingabe in mehreren aufeinanderfolgenden Runden verarbeitet wird, die gleich aufgebaut sind (Rundenfunktion).
Die Schwierigkeit, eine Verschlüsselung zu entwickeln, liegt darin, eine umkehrbare Transformation zu finden, welche den kryptographischen Anforderungen (Konfusion und Diffusion) gerecht wird und mit nicht zu hohem Aufwand implementierbar und effizient ausführbar ist. Darum versucht man meist nicht, eine komplexe Funktion zu finden, die den Text in einem einzigen Schritt verschlüsselt, sondern beschränkt sich auf eine relativ einfach aufgebaute Rundenfunktion. Erst deren mehrfache Anwendung ergibt eine ausreichend komplexe Verschlüsselungsfunktion. Die Rundenfunktion bewirkt sowohl Konfusion als auch Diffusion, wodurch diese während der Verschlüsselung wirksam miteinander verzahnt werden. Es werden genügend Runden durchlaufen, um den Datenblock mehrmals vollständig zu durchmischen, meist etwa 8 bis 64 Runden. Die Rundenfunktion wird außerdem so aufgebaut, dass sich die Diffusionseigenschaften zwischen Ver- und Entschlüsselung nicht wesentlich unterscheiden und somit auch beim Entschlüsseln eine gute Diffusion besteht.
Die aufeinanderfolgenden Runden sollten nicht exakt gleich arbeiten, da das Verfahren sonst für den sogenannten Slide-Angriff (engl. slide attack) anfällig wäre.[1] Deshalb berechnet man üblicherweise aus dem Benutzerschlüssel mehrere verschiedene Rundenschlüssel, und in jeder Runde wird ein anderer davon mit dem Datenblock verknüpft, entweder als zweite Eingabe in die Rundenfunktion:
- ,
oder zwischen den Anwendungen der Rundenfunktion, z. B. durch bitweise XOR-Verknüpfung:
mit Rundennummer . Dabei ist die Rundenfunktion, der Klartext, der Geheimtext, der Benutzerschlüssel und die Schlüsseleinteilungsfunktion, die die einzelnen Rundenschlüssel liefert. Sich zyklisch alle Runden wiederholende Rundenschlüssel sollten vermieden werden, da dies ebenfalls einen Slide-Angriff ermöglichen würde.
Außerdem ist es ungünstig, wenn Abschnitte der Verschlüsselung (eine oder einige aufeinanderfolgende Runden) mit zu wenig Schlüsseldaten erfolgen, da das Verfahren dann für den Meet-in-the-middle-Angriff anfällig wäre. Das kann sich beispielsweise dadurch ergeben, dass die während der ersten Hälfte der Verschlüsselung (Runden bis ) verwendeten Rundenschlüssel nur von einer Hälfte des Benutzerschlüssels abhängen und die restlichen Rundenschlüssel ( bis ) nur von der zweiten Hälfte. Die Rundenschlüssel sollten ausreichend viele und ausreichend lang sein und jeder Rundenschlüssel sollte vom gesamten Benutzerschlüssel (statt nur von einem Teil davon) abhängen. Idealerweise ist die Schlüsseleinteilungsfunktion ein Hashprozess, der die Rundenschlüssel auf komplexe, pseudozufällige Weise aus dem Benutzerschlüssel berechnet.
Damit man die Implementierung einer Chiffre gut gegen Seitenkanalangriffe absichern kann, sollte die Art und die Reihenfolge der beim Verschlüsseln ablaufenden Operationen nicht vom Schlüssel oder vom Klartext abhängen. Nur die Werte der Operanden sollten sich jeweils ändern. Ein Angreifer, der den Ablauf von außen verfolgen kann, etwa indem er die Zeit eines Verschlüsselungsvorgangs misst, soll keine Rückschlüsse auf die verarbeiteten Daten ziehen können. Wenn zum Beispiel abhängig von einem Bit des Schlüssels (bzw. eines Rundenschlüssels) an einer Stelle entweder eine Addition oder eine Multiplikation zweier Werte erfolgt, dann ist es schwer zu vermeiden, dass diese Operation je nach Schlüsselbit unterschiedlich lange dauert und der Prozessor dabei auch unterschiedlich viel Energie verbraucht und das Schlüsselbit dadurch von einem Angreifer ermittelt werden kann.
Feistelchiffre
[Bearbeiten | Quelltext bearbeiten]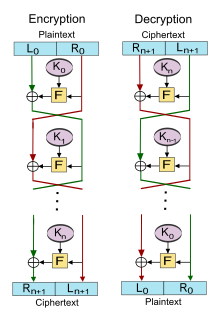
Das Feistelnetzwerk ist eine allgemeine Struktur, mit der Blockchiffren realisiert werden können. Horst Feistel, der im Jahr 1970 bei IBM an der Chiffre Lucifer arbeitete, gilt als Erfinder. Ein Klartextblock wird in zwei Teile geteilt und in mehreren Runden verarbeitet. In jeder Runde wird ein Blockteil zusammen mit einem Rundenschlüssel in die Rundenfunktion eingegeben und deren Ausgabe mit dem anderen Blockteil verknüpft. Feistelnetzwerke ermöglichen eine Entschlüsselung, ohne dass die Umkehrung der Rundenfunktion berechnet werden muss. Viele Chiffren, zum Beispiel DES, Twofish und Blowfish, sind als Feistelnetzwerke aufgebaut.
Lai-Massey-Chiffre
[Bearbeiten | Quelltext bearbeiten]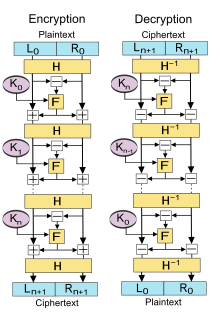
Hier nutzt man, ähnlich wie beim Feistelnetzwerk, eine Rundenfunktion auf eine Weise, dass man beim Entschlüsseln nicht ihre Umkehrung berechnen muss. Der Datenblock wird in zwei Hälften geteilt. In jeder Runde verknüpft man beide Hälften miteinander, gibt das Ergebnis in die Rundenfunktion ein und verknüpft dann deren Ausgabe mit jeder der Blockhälften:
- .
Das geschieht so, dass ist und man somit bei Wiederholung der Operation wieder die gleiche Eingabe in erhält. So ist es leicht, die Runde rückgängig zu machen. Am einfachsten geht das, indem man für und jeweils das bitweise XOR einsetzt. Eine weitere Möglichkeit ist, für die Subtraktion zu verwenden, und für beim Verschlüsseln die Addition und beim Entschlüsseln die Subtraktion (oder umgekehrt), jeweils modulo , wobei die Wortbreite in Bit ist.
Damit sich die aufeinanderfolgenden Runden beim Verschlüsseln nicht gegenseitig schwächen oder aufheben, muss der Datenblock zwischen den Runden mit einer weiteren Operation modifiziert werden. Dazu werden häufig die Bits einer Blockhälfte permutiert, z. B. durch Bitrotation.
Lai-Massey-Chiffren sind eher selten, Beispiele sind IDEA und IDEA NXT.
Substitutions-Permutations-Netzwerk
[Bearbeiten | Quelltext bearbeiten]
Die Runden eines Substitutions-Permutations-Netzwerks sind dreiteilig: Zuerst wird der Rundenschlüssel mit dem Datenblock verknüpft. Dann wird eine S‑Box auf den Datenblock angewendet, der dazu in Teile von Bit geteilt wird, die für sich substituiert werden. Danach werden die Bits des Datenblocks permutiert, so dass die Ausgabe einer S‑Box sich in der nächsten Runde auf mehrere S‑Boxen und schließlich über den ganzen Datenblock verteilt. Oft wird diese Permutation durch eine komplexere Operation ersetzt, wie z. B. bei Serpent und AES, um die Diffusion zu beschleunigen. In der letzten Runde ist die Permutation überflüssig, stattdessen wird noch einmal mit einem Rundenschlüssel verknüpft.
Zur Entschlüsselung müssen diese drei Schritte invertiert werden. Die S‑Box muss bijektiv sein, und beim Entschlüsseln muss die dazu inverse S‑Box eingesetzt werden.
Primitive
[Bearbeiten | Quelltext bearbeiten]Als Einzeloperationen in der Rundenfunktion (sog. kryptographische Primitive) werden meistens solche gewählt, die von den verbreiteten Mikroprozessoren durch einen einzigen Maschinenbefehl schnell ausführbar sind, damit sich die Verschlüsselung einfach und effizient in Software programmieren lässt:
- Addition, Subtraktion und Multiplikation von Ganzzahlen modulo , wobei die Breite eines Datenwortes in Bit ist
- bitweise boolesche Verknüpfungen: UND, ODER, XOR, NICHT
- Bitrotation
- Bitverschiebung
Bei Bitrotation und -verschiebung kann die Schiebeweite konstant, schlüsselabhängig (z. B. CAST) oder datenabhängig (RC5, RC6, MARS) sein.
Viele moderne Blockchiffren sind sogenannte ARX-Chiffren, wie etwa Threefish. Das bedeutet, sie sind nur aus Addition, Rotation mit konstanter Weite und XOR aufgebaut. Dadurch sind sie einfach implementierbar und effizient, obwohl meist viele Runden für eine ausreichende Stärke der Verschlüsselung nötig sind.
S-Boxen sind in Software weniger effizient zu implementieren, aber sie sind auch starke Konfusionserzeuger und somit kryptographisch sehr wirksam, denn man kann (weitgehend) frei bestimmen, wie die eingegebenen Bits von einer S-Box auf die Ausgabebits abgebildet werden. S-Boxen können konstant (DES, AES, CAST) oder schlüsselabhängig (Blowfish) sein.
Im Hinblick auf die Implementierung in Hardware nutzt man in vielen Chiffren auch die Permutation von Bits (reichlich z. B. bei DES), die sich hier einfach realisieren lässt, man muss nur jede Bit-Leitung an den richtigen Eingang des nachfolgenden Gatters legen. Bei Software-Implementierung sind allgemeine Bitpermutationen hingegen ungeschickt, man muss das Datenwort in einzelne Bits zerteilen, diese verschieben und neu zusammensetzen. Meist lässt sich das am einfachsten als S‑Box darstellen, die z. B. immer 8 Bit durch ein ganzes Wort ersetzt, das die eingegebenen Bits an den richtigen Positionen enthält, wonach diese Wörter durch bitweises ODER zusammengesetzt werden. Eine Substitution mit anschließender Bitpermutation kann mit dieser Technik zu einer Operation zusammengefasst werden.
Kryptographische Betriebsmodi
[Bearbeiten | Quelltext bearbeiten]Ein kryptographischer Betriebsmodus legt fest, wie sich die Verschlüsselung mehrerer Klartextblöcke vollzieht, indem er definiert, in welcher Art der Verschlüsselungsalgorithmus auf den Datenstrom angewandt wird.[2] Je nach den Anforderungen der Anwendung variiert die Fehleranfälligkeit und Sicherheit. Der internationale Standard ISO 10116 definiert für blockorientierte Verschlüsselungsalgorithmen vier verschiedenen Betriebsarten:
- Electronic Code Book (ECB): Jeder Block wird für sich verschlüsselt.
- Cipher Block Chaining (CBC): Jeder Block wird mit dem vorherigen Geheimtextblock XOR-verknüpft, bevor man ihn verschlüsselt.
- Cipher Feedback (CFB): Ein Geheimtextblock entsteht durch XOR des Klartextblocks mit dem nochmals verschlüsselten vorherigen Geheimtextblock.
- Output Feedback (OFB): Die Blockchiffre wird wie eine Stromchiffre eingesetzt, indem ein Initialisierungsvektor immer wieder überschlüsselt wird, um damit jeweils den nächsten Klartextblock per XOR zu verknüpfen.
Außerdem gibt es den Counter Mode (CTR), bei dem eine Nonce zusammen mit der Nummer eines Blocks verschlüsselt wird. Das Ergebnis wird nach Art einer Stromverschlüsselung mit diesem Block XOR-verknüpft.
Einige neuere Blockverschlüsselungen, wie z. B. Threefish, nehmen eine zusätzliche Eingabe, den sogenannten Tweak, entgegen, der die Abbildung des Klartextes auf den Schlüsseltext beeinflusst. Auf Englisch nennt man sie tweakable block ciphers; eine deutsche Übersetzung hat sich bisher nicht verbreitet. Bei Änderung des Tweak ändert sich die Permutation der Blockwerte, ebenso wie bei Änderung des Schlüssels. Während aber letztere durch die komplexe Schlüsseleinteilung vieler Chiffren aufwändig ist (ein extremes Beispiel ist Blowfish), kann der Tweak sehr einfach und schnell geändert werden. Dadurch werden weitere Betriebsmodi möglich. So kann man ECB derart modifizieren, dass jeder Block mit einem anderen Tweak (aber gleichem Schlüssel) verschlüsselt wird. Der Tweak muss nicht geheim gehalten werden, und man kann dafür z. B. einfach die laufende Nummer des Blocks verwenden. Dadurch werden gleiche Klartextblöcke nicht mehr auf gleiche Geheimtextblöcke abgebildet.
Auch Blockchiffren, die an sich nicht tweak-bar sind, können durch Wahl eines geeigneten Betriebsmodus mit einem Tweak verschlüsseln. Das nutzt man zum Beispiel bei XTS-AES.
Bekannte Blockchiffren
[Bearbeiten | Quelltext bearbeiten]Einige bekannte Blockchiffren sind:
- Camellia
- RC2
- Data Encryption Standard (DES)
- Triple-DES (3DES)
- International Data Encryption Algorithm (IDEA)
- IDEA NXT (FOX)
- RC5
- RC6
- MARS
- Serpent
- Advanced Encryption Standard (AES)
- CAST
- Blowfish
- Twofish
- Threefish
- Skipjack
- FEAL
- Tiny Encryption Algorithm (TEA)
- Extended Tiny Encryption Algorithm (XTEA)
- SEED
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Klaus Pommerening: Bitblock-Verschlüsselung. (PDF; 712 kB) Fachbereich Mathematik der Johannes-Gutenberg-Universität
- Stefan Labitzke, Sven Kampfhenkel: Sicherheitsaspekte in der Softwaretechnik. (PDF; 1,7 MB), Fakultät IV Informatik der TU Berlin
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Alex Biryukov und David Wagner über slide attacks (PDF; 196 kB)
- ↑ Bruce Schneier: Applied Cryptography. Protocols, Algorithms and Source Code in C. 2. Auflage. John Wiley & Sons, New York 1996, ISBN 0-471-11709-9, S. 206–208.








































