Eulersches Tonnetz
Die Eulerschreibweise ist nach dem Mathematiker Leonhard Euler benannt, der diese für die Feinanalyse von Musikstücken in reiner Stimmung einführte. Dabei wird schon bei der Bezeichnungsweise erkennbar, ob die vorkommenden Terzen und Quinten rein erklingen. Zum Beispiel haben die Tonika-, Subdominant- und Dominantakkorde der reinen C-Dur-Tonleiter die Darstellung c - ,e - g[1] und f-,a-c sowie g-,h-d (Durakkorde mit reiner großer und kleiner Terz sowie reiner Quinte), wobei das „Tiefkomma“ vor ,e und ,a sowie ,h besagt, dass die Töne jeweils ein syntonisches Komma tiefer erklingen als das e und a sowie h in der Reihe der reinen Quinten … f c g d a e h …
Das Eulersche Tonnetz stellt den Tonumfang der reinen Stimmung in einem zweidimensionalen Gitternetz aus reinen Quint- und Terzintervallen dar. Euler hatte sich bereits in dem 1739 erschienenen Werk Tentamen novae theoriae musicae[2] eingehend mit den mathematischen Zusammenhängen der Musik befasst. In diesem Werk suchte er eine mathematische Begründung für das Konsonanz- und Dissonanzempfinden in der Tonkunst und stellte ein Intervallverwandtschaftssystem auf der Primzahlenbasis zusammen. In einem weiteren Werk De harmoniae veris principiis per speculum musicum repraesentatis,[3] das 1773 veröffentlicht wurde, beschrieb er das Tonnetz aus Quinten und Terzen.
Das Quint-Terz-Schema[Bearbeiten | Quelltext bearbeiten]
Die Einführung der reinen Großterz (mit dem Saitenlängenverhältnis zwischen unterem und oberem Ton von 5:4) – als Ersatz und Vereinfachung des pythagoreischen Ditonus (81:64) – geht zurück auf die enharmonische Tetrachordteilung Didymos’ (etwa 100 Jahre nach Pythagoras). Allerdings ist das Tonsystem im antiken Griechenland nicht mit dem Tonsystem zu vergleichen, auf das sich Leonhard Euler bezieht. In unserem heutigen Tonsystem erstmals erwähnt wurde die reine große Terz um 1300 von Walter Odington in seiner Schrift De Speculatione Musices.[4][5]
In der abendländischen Musik wurde die Großterz (Frequenzverhältnis: 81:64) des pythagoreischen Systems als Dissonanz empfunden. Mit dem Aufkommen der Mehrstimmigkeit emanzipierte sich im 15. Jahrhundert die reine Großterz (5:4), die als Bestandteil des Dreiklanges zunehmend an musikalischer Bedeutung gewann.
Der C-Dur Akkord in der Obertonreihe?
Hierbei erhält man ein Tonsystem, das auf den Intervallen Oktave 2⁄1, Quinte 3⁄2 und Terz 5⁄4 basiert. Die anderen Intervalle des Quint-Terz-Systems lassen sich so als Vielfache dieser Intervalle darstellen.
Aus der Vielzahl von Kombination dieser Intervalle ergibt sich ein (theoretisch) unendlicher Tonraum. Dieser Tonraum wird häufig mittels eines Tonnetzes wie folgt grafisch dargestellt:
Darstellung im Tonnetz[Bearbeiten | Quelltext bearbeiten]
Da die reine Terz nicht mit Quinten darstellbar war, stellte Leonhard Euler das Beziehungsgeflecht der reinen Stimmung mit Hilfe von Quintenreihen dar, die sich jeweils um ein syntonisches Komma unterscheiden. Im folgenden Beziehungsgeflecht reihen sich die Quinten in horizontaler Richtung und die Terzen in vertikaler Richtung.
Die Schreibweise ,x („Tiefkomma x“) bzw. ’x („Hochkomma x“) – das Komma vor der Tonbezeichnung – usw. bedeutet, dass der Ton ,x bzw. ’x ein syntonisches Komma tiefer bzw. höher als der Ton x ist.[6]
Diese grafische Darstellung des Quint-Terz-Schemas versteht sich als Beziehungsgeflecht von Tonigkeiten ohne fixierte Oktavlage (auch: „Chroma“, „Toncharakter“;[7] englisch pitch class), so dass zur Berechnung konkreter Intervallverhältnisse noch das entsprechende Vielfache der Oktave 2⁄1 hinzu- oder weggenommen werden muss.
Die reinen Tonleitern haben in dieser grafischen Darstellung ein stets gleiches Erscheinungsbild. Intervallzusammenhänge sind für jede Tonleiter immer gleich:
| Tonleiter | Tonleitertöne tabellarisch aufgelistet | ||||||||||||||||
| F-Dur | f | g | ,a | b | c | ,d | ,e | f | ,d-Moll | ,d | ,e | f | ,g | ,a | b | c | ,d |
| C-Dur | c | d | ,e | f | g | ,a | ,h | c | ,a-Moll | ,a | ,h | c | ,d | ,e | f | g | ,a |
| G-Dur | g | a | ,h | c | d | ,e | ,fis | g | ,e-Moll | ,e | ,fis | g | ,a | ,h | c | d | ,e |
| x-Dur | x | x | ,x | x | x | ,x | ,x | x | x-Moll | x | x | ’x | x | x | ’x | ’x | x |
(Umfangreichere Tabelle siehe Die Tonleitern im Quintenzirkel)
Die Berechnung der zugehörigen Centwerte am Beispiel der Töne c - e - ,e mit Oktave = 1200 Cent, Quinte = 701,955 Cent und syntonisches Komma = 21,506 Cent ergibt zum Beispiel mit c = 0 Cent gerundet:
- e = c + 4 Quinten − 2 Oktave = 408 Cent und ,e = e − syntonisches Komma = 386 Cent ( = c + reine große Terz)
Die entsprechenden Frequenzwerte berechnen sich mit c = 264 Hz zu:
- .
Die Centwerte der Töne ergeben sich zu:
| Ton | Berechnung | Centwert |
|---|---|---|
| c | 0 | 0 |
| d | 2q − o | 204 |
| ,e | 4q − 2o − k | 386 |
| f | −q + o | 498 |
| g | q | 702 |
| ,a | 3q − o − k | 884 |
| ,h | 5q − 2o − k | 1088 |
| c′ | o | 1200 |
(Umfangreichere Tabelle siehe Die Tonleitern im Quintenzirkel)
Es zeigt die Tonbeziehungen der harmonisch-reinen Stimmung. Zum Beispiel erklingen die Töne ,e und ,a sowie ,h der C-Dur-Tonleiter ein syntonisches Komma tiefer als in der pythagoreischen Quintenkette. Die Akkorde c-,e-g und f-,a-c sowie g-,h-d bestehen aus reine Terzen ( 5⁄4 und 6⁄5) und reinen Quinten ( 3⁄2).[8]
Das eigentliche „Tonnetz“ wurde 1773 von Leonhard Euler als speculum musicum („Abbild der Musik“) in seiner gleichnamigen Schrift De harmoniae veris principiis per speculum musicum repraesentatis vorgestellt, und von da an – zusammen mit den von Moritz Hauptmann[9] eingeführten Bezeichnungen für bisher gleichnamige Töne, die sich um ein syntonisches Komma unterscheiden – von zahlreichen Theoretikern zu verschiedenen Zwecken abgewandelt (u. a. von Hermann v. Helmholtz[10], Arthur v. Oettingen[11] und Hugo Riemann[12]). Die unterschiedlichen Charaktere von Tönen gleichen Namens, aber verschiedener Lage im (unendlichen) Tonraum ergibt sich in harmonisch-reiner Stimmung nicht nur aus einer jeweils anderen Tonumgebung und Harmonisierung (etwa das ,e im C-dur-Akkord c-,e-g und das e im E-dur-Akkord e-,gis-h), sondern auch aus einem (minimalen) Tonhöhenunterschied zwischen den jeweiligen Tonstufen (,e und e):
In der C-Dur-Tonleiter c d ,e f g ,a ,h c ist das Intervall c-,e eine große Terz mit dem Frequenzverhältnis 5⁄4. In der Quintenreihe c-g-d-a-e ist das Intervall (zurückoktaviert) c-e eine pythagoreische Terz mit dem Frequenzverhältnis 81⁄64. Diese beiden Intervalle unterscheiden sich um das syntonische Komma mit dem Frequenzverhältnis 81⁄80.[13]
Die C-Dur-Tonleiter in harmonisch-reiner Quint-Terz Stimmung[Bearbeiten | Quelltext bearbeiten]
Die reine C-Dur-Tonleiter kann verstanden werden als Auswahl derjenigen sieben Tonstufen aus dem Quint-Terz-Schema, die zur Intonation der drei Hauptfunktionen Subdominante (S), Tonika (T) und Dominante (D) – also für die „authentische“ Kadenz benötigt werden:
C-Dur-Tonalität
Die eigentliche Skala entsteht durch Transposition dieser Tonstufen in die entsprechende Oktavlage – beispielsweise zwischen c1 und c2. Sie besteht nun – im Gegensatz zur pythagoreischen Skala – nicht mehr aus zwei, sondern aus drei Intervallschritten verschiedener Größe, dem großen Ganzton 9⁄8, dem kleinen Ganzton 10⁄9 und dem diatonischen Halbton 16⁄15 :
reine C-Dur-Tonleiter
Die These (zum Beispiel bei Sigfrid Karg-Elert), dass bei dieser siebenstufigen Tonleiter, welche die harmonisch-reine Intonation der Hauptfunktionen T, S und D erlaubt, melodisch unsauber wirkt, da die jeweiligen Terzen ,e / ,a und ,h in melodischen Zusammenhang als zu niedrig empfunden werden können, ist umstritten. Ross W. Duffin[14] belegt, dass die „Expressive Intonation“, d. h. die Verwendung von geschärften Leittönen, vor allem seit Pablo Casals (1876–1973) eine durchaus moderne Erscheinung ist. Er erwähnt etwa: Hermann von Helmholtz, der das Spiel von Joseph Joachim physikalisch untersuchte, stellte fest, dass Joachim die Terzen (fast) rein intonierte, was sich auch in seinen Schallplattenaufnahmen von 1903 – trotz technischer Mängel – bestätigt.
Anwendung des Eulerschen Tonnetzes zur musikalischen Feinanalyse[Bearbeiten | Quelltext bearbeiten]
Siehe auch Feinanalyse bei Intonationsproblemen
Beispiel 1: Dreiklang auf der II. Stufe in C-Dur[Bearbeiten | Quelltext bearbeiten]
Vergleicht man die beiden Dreiklänge
- Dreiklang auf der 2. Stufe ,d - f - ,a (Mollakkord mit reiner kleiner und großer Terz) und
- Dreiklang auf der 5. Stufe g - ,h - d (Durakkord mit reiner großer und kleiner Terz)
so erkennt man sofort, dass sich die Töne d und ,d um ein syntonisches Komma unterscheiden.
Siehe dazu auch Beispiel 3.
Beispiel 2: Unterschied Gis und As[Bearbeiten | Quelltext bearbeiten]
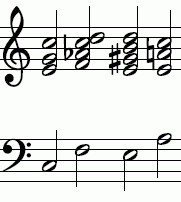
|
Akkorde (mit Frequenzen in Hertz)
C-Dur Tonika: c(132) c′(264) ,e′(330) g′(396) c″(528) C-Dur Subdominante in Moll mit Sixte ajoutée: f(176) f′(352) ’as′(422,4) c″(528) d″(594) a-Moll Dominantseptimenakkord: ,e(165) ,e′(330) ,,gis′(412,5) ,h′(495) d″(586,7) a-Moll Tonika: ,a(220) ,e′(330) ,a′(440) c″(528) As ist hier um 9,9 Hz höher als Gis mit dem Frequenzverhältnis AS/Gis = 128⁄125 (41 Cent). Bei diesem Intervall handelt es sich um die kleine Diësis.[15] |
Beispiel 3: Die „Kommafalle“[Bearbeiten | Quelltext bearbeiten]
Gerade Chöre, die besonders gut aufeinander hören, können detonieren. Dies liegt dann oft an der unterschiedlichen Intonation gleichnamiger Töne. Dies ist schon lange bekannt. Die musikalische Feinanalyse darüber, die mit Hilfe der Bezeichnungen des Eulerschen Tonnetzes leichter zu verstehen ist, gehört jedoch nicht zum musikalischen Bildungsgut.[16]
Ein klassisches Beispiel einer Kommafalle ist das Vorkommen des Akkordes der II. Stufe:
Der dritte Akkord f-,a-d klingt in C-Dur unrein. Ein Chor, bei dem die Stimmen aufeinander hören, singt das passende d ein syntonisches Komma tiefer, hier mit ,d bezeichnet. Es handelt sich ja um die Moll-Parallele zum F-Dur-Akkord und die F-Dur-Tonleiter ist f-g-,b-c-,d-,e-f. Im folgenden Akkord g-,h-d muss dann jedoch wieder das „richtige“ d von C-Dur gesungen werden.
Wird dies nicht beachtet, tappt man in die Kommafalle, wie im folgenden Hörbeispiel gezeigt wird. Nach viermaliger Wiederholung erklingt der Tonsatz fast einen halben Ton tiefer. Das viermalige Wiederholen der Kommafalle ergibt ein Detonieren um fast einen Halbton
| Tonika | ,e | g | c | |
| Subdominante | f | ,a | c | |
| Subdominantenparallele | f | ,a | ,d | |
| Dominante | ,g | ,,h | ,d | Bei gleichem ,d des Soprans ein (syntonisches) Komma zu tief |
| Tonika | ,,e | ,g | ,c | Ein Komma zu tief |
| Subdominante | ,f | ,,a | ,c | Ein Komma zu tief |
| Subdominantenparallele | ,f | ,,a | ,,d | Ein Komma zu tief |
| Dominante | ,,g | ,,,h | ,,d | Bei gleichem ,,d des Soprans nun zwei Kommata zu tief |
| Tonika | ,,,e | ,,g | ,,c | Zwei Kommata zu tief |
| Subdominante | ,,f | ,,,a | ,,c | Zwei Kommata zu tief |
| Subdominantenparallele | ,,f | ,,,a | ,,,d | Zwei Kommata zu tief |
| Dominante | ,,,g | ,,,,h | ,,,d | Bei gleichem ,,,d des Soprans nun drei Kommata zu tief |
| Tonika | ,,,,e | ,,,g | ,,,c | Drei Kommata zu tief |
| Subdominante | ,,,f | ,,,,a | ,,,c | Drei Kommata zu tief |
| Subdominantenparallele | ,,,f | ,,,,a | ,,,,d | Drei Kommata zu tief |
| Dominante | ,,,,g | ,,,,,h | ,,,,d | Bei gleichem ,,,d des Soprans nun vier Kommata zu tief |
| Tonika | ,,,,,e | ,,,,g | ,,,,c | Vier Kommata (86 Cent) zu tief |
Der Quintenzirkel im Eulerschen Tonnetz[Bearbeiten | Quelltext bearbeiten]
Zur nächsten Tonart ändern sich jeweils zwei Töne. Der chromatische Halbton mit 92,179 Cent (Frequenzverhältnis: 135⁄128) ist im Notenbild erkennbar, die Veränderung um ein syntonisches Komma mit 21,506 Cent (Frequenzverhältnis 81⁄80) ist hier an der geänderten Cent-Angabe ablesbar.
Die ♯-Tonarten im Eulerschen Tonnetz

- C-Dur: c(0) d(204) ,e(386) f(498) g(702) ,a(884) ,h(1088) c
- G-Dur: g a(906) ,h c d ,e ,fis(590) g
- D-Dur: d e(408) ,fis g a ,h ,cis(92) d
- A-Dur: a h(1110) ,cis d e ,fis ,gis(794) a
- E-Dur: e fis(612) ,gis a h ,cis ,dis(296) e
- H-Dur: h cis(114) ,dis e fis ,gis ,ais(998) h
- FIS-Dur: fis gis(816) ,ais h cis ,dis ,eis(500) fis
- CIS-Dur: cis dis(318) ,eis fis gis ,ais ,his(2) cis
Die ♭-Tonarten im Eulerschen Tonnetz (Cent-Werte in Klammern)
- C-Dur: c(0) d(204) ,e(386) f(498) g(702) ,a(884) ,h(1088) c
- F-Dur: f g ,a b(996) c ,d(182) ,e f
- B-Dur: b c ,d es(294) f ,g(680) ,a b
- Es-Dur: es f ,g as(792) b ,c(-22) ,d es
- As-Dur: as b ,c des(90) es ,f(477) ,g as
- Des-Dur: des es ,f ges(588) as ,b(975) ,c des
- Ges-Dur: ges as ,b ces(1086) des ,es(273) ,f ges
- Ces-Dur: ces des ,es fes(384) ges ,as(771) ,b ces
Schon Andreas Werckmeister stellte fest, dass die enharmonische Gleichsetzung möglich ist, wenn man von der Abweichung um ein Schisma (< 2 Cent) absieht. Er vernachlässigte dieses Intervall von unter 2 Cent, weil es auf dem Monochord „kaum einen Circulstrich“ ausmache[18]:
- ,h(1088)=ces(1086)
- ,his(2)=c(0)
- ,cis(92)=des(90)
- ,dis(296)=es(294)
- ,e(386)=fes(384)
- ,eis(500)=f(498)
- ,fis(590)=ges(588)
- ,gis(794)=as(792)
- ,ais(998)=b(996)

Bei Beschränkung auf die 15 Dur-Tonleitern von ces-Dur (7♭) bis cis-Dur (7♯) und die 3 mal 15 Molltonarten von ,as-Moll (7♭) bis ,ais-Moll (7♯) genügen die 53 bräunlich gefärbten Töne pro Oktave, um in reiner Stimmung zu spielen. Die römischen Zahlen beziffern die Stufen der Tonleiterbeispiele. Alle 60 Tonleitern ergeben sich bei horizontalem Verschieben der farbigen Gerüste innerhalb der Graphik. Die grau dargestellten und alle nicht abgebildeten Töne des unendlich fortsetzbaren Netzes werden für die 60 Tonleitern nicht benötigt.
Der Abstand von 18 Tönen zum nachsthöheren unterscheidet sich um ein Schisma (1,95 cent) (siehe Tabelle oben). Dieser Unterschied ist unhörbar klein. Die Zahl der für die reine Stimmung nötigen Töne pro Oktave verringert sich dadurch auf 53-18=35. Im Tonnetz befinden sich die 18 niederen Töne der engen Intervalle in der 3. Zeile von fes bis c und in der 2. Zeile von ,des bis ,a. Die 18 höheren Töne liegen jeweils 8 Quint-Schritte nach rechts und einen Großterz-Schritt nach oben versetzt. Der unhörbare kleine Cent-Unterschied ergibt sich mit weiteren 5 Oktavschritten abwärts.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Euler, Leonhard. In: Musik in Geschichte und Gegenwart, Band 3, 1616
- Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863 (Nachdruck: Minerva-Verlag, Frankfurt am Main 1981, ISBN 3-8102-0715-2, Auszug).
- Ludwig Riemann: Populäre Darstellung der Akustik in Beziehung zur Musik. Im Anschluss an Hermann von Helmholtz’ „Lehre von den Tonempfindungen“. Vieweg, Braunschweig 1896.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Reine Stimmung
- Reine Stimmung bei Tasteninstrumenten
- Tonstruktur (mathematische Beschreibung)
- Modulation bei reiner Stimmung
- Tonic sol-fa, dort auch der Bericht von Hermann von Helmholtz, einem Verfechter der reinen Stimmung
- Vogelsches Tonnetz, eine Erweiterung des Eulerschen Tonnetzes um Septimen
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Joachim Mohr: Die Eulerschreibweise.
- Auf der PC-Tastatur ausprobieren. Kostenloses Java-Applet
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Bei Euler c-e-g mit Unterstrich
- ↑ Leonhard Euler: Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae. St. Petersburg 1739.
- ↑ Leonhard Euler: De harmoniae veris principiis per speculum musicum repraesentatis. In: Novi Commentarii academiae scientiarum Petropolitanae, 18, St. Petersburg 1774.
- ↑ Walter Odington
- ↑ The Harvard dictionary of music. Don Michael Randel, 2003, ISBN 0-674-01163-5, S. 56, Überschrift: Arithmetic and harmonic mean, Abschnitt 2 (online).
- ↑ Häufig wird auch folgende Schreibweise verwendet: („unterstrichen x“) statt („Tiefkomma x“) und („überstrichen x“) statt ’x („Hochkomma x“)
- ↑ Jacques Handschin: Der Toncharakter. Eine Einführung in die Tonpsychologie. Zürich 1948.
- ↑ Carl Dahlhaus: Untersuchungen über die Entstehung der harmonischen Tonalität. Kassel 1965. Renate Imig: Systeme der Funktionsbezeichnung in den Harmonielehren seit Hugo Riemann. Düsseldorf 1970.
- ↑ Moritz Hauptmann: Die Natur der Harmonik und Metrik. Leipzig 1853.
- ↑ Hermann v. Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Braunschweig 1863.
- ↑ Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik. Dorpat/Leipzig 1866; überarbeitete zweite Auflage als Das duale Harmoniesystem, Leipzig 1913.
- ↑ z. B.: Hugo Riemann: Ideen zu einer „Lehre von den Tonvorstellungen“. In: Jahrbuch Peters 21/22, 1914/15
- ↑ Martin Vogel: Die Lehre von den Tonbeziehungen. Bonn - Bad Godesberg 1975, S. 103f.
- ↑ Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You Should Care). W. W. Norton & Company, New York NY 2007, ISBN 978-0-393-06227-4 (Exzerpt).
- ↑ Für den Fachmann die Berechnung der Frequenzen mit c′ = 264 Hz:
,,gis′ = Hz = 422,4 Hz,
’as′ = Hz = 412,5 Hz,
Berechnung mit Oktave = 1200·lb(2), Quinte = 1200·lb( 3⁄2), Komma = 1200·lb(81/8o) und c = 0 Cent:
,,gis = 8 Quinten − 4 Oktaven − 2 Komma = 772,627 Cent,
’as = −4 Quinten + 3 Oktaven + Komma = 813,686 Cent,
Differenz = as′ − ,,gis = 41,059 Cent - ↑ Bettina Gratzki S. 76: Die reine Intonation im Chorgesang (= Orpheus-Schriftenreihe zu Grundfragen der Musik 70). Verlag für systematische Musikwissenschaft GmbH, Bonn 1993, ISBN 3-922626-70-X (Exzerpt ( des vom 19. Februar 2014 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.).
- ↑ Mit q = 701,955 (Quinte) und t = 386,314 (Terz) errechnet sich (modulo Oktave = 1200): c = 0, g = q, d = 2q, a = 3q, e = 4q usw. f = −q, b = −2q, es = −3q usw. Mit s = 21,506 (syntonisches Komma): ,c = c − s, ,g = g − s, ,d = d − s, … ,f = f − s, ,b = ,b − s, ,es = es −s usw.
- ↑ Andreas Werkmeister: Musikalische Temperatur. Quedlinburg 1691.










