Diatonik
Diatonik (von altgriechisch διάτονος diátonos „durch Ganztöne gehend“,[1][2] zu διά „durch“ und τόνος „Anspannung, Ton“[3]), ein meist adjektivisch verwendeter Begriff der Musiktheorie, kennzeichnet bestimmte Tonbeziehungen in Tonsystemen[4][5] und Tonleitern[6]. Diatonische Tonleitern etwa sind spezielle, aus Ganzton- und Halbtonschritten zusammengesetzte, in der Regel siebenstufige Tonleitern. Seit dem frühen Mittelalter[7] bildeten diatonische Tonleitern die Grundlage der abendländischen Musik, zunächst in Form der Kirchentonarten, später als Dur-Moll-System. Um die Wende zum 20. Jahrhundert löste sich ein Teil der Komponisten von der diatonischen Dur-Moll-Tonalität.[8]
Neben dem Begriff der diatonischen Tonleiter gibt es den des diatonischen Halbtons; man spricht vom diatonischen Halbton d-es im Gegensatz zum chromatischen Halbton d-dis. Des Weiteren gibt es diatonische Tetrachorde, welche definiert sind als Viertonfolgen, bestehend aus zwei Ganztonschritten und einem Halbtonschritt.
Diatonische Tonleiter[Bearbeiten | Quelltext bearbeiten]
Definition über Stammtöne[Bearbeiten | Quelltext bearbeiten]
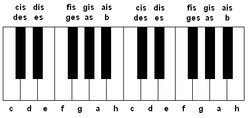

Eine diatonische Tonleiter ist eine siebenstufige (heptatonische) Tonleiter, die den Oktavraum in fünf Ganz- und zwei Halbtonschritte aufteilt und folgende Eigenschaften hat:
- Alle Tonleiterstufen sind von verschiedenen Stammtönen abgeleitet, was sich äußerlich darin spiegelt, dass ihre Bezeichnungen alle mit verschiedenen Buchstaben anfangen.
- Zwischen benachbarten Stufen treten keine übermäßigen oder verminderten Intervalle auf.
Zum Beispiel:
- C-D-E-F-G-A-H
- H-Cis-Dis-E-Fis-Gis-Ais
- Des-Es-F-Ges-As-B-C
- D-E-Fis-G-A-H-Cis-D
Keine diatonische Tonleiter nach dieser Definition wäre (da zweimal der Stammton G benutzt wird):
- D-E-Ges-G-A-H-Cis-D
Man beachte, dass bei dieser Definition die Existenz von Stammtönen, d. h. Notennamen, vorausgesetzt wird.
Klassische Definition ohne Stammtöne[Bearbeiten | Quelltext bearbeiten]
Eine diatonische Tonleiter ist eine siebenstufige Tonleiter, die den Oktavraum in fünf Ganz- und zwei Halbtonschritte aufteilt, so dass die Halbtonschritte maximal weit voneinander entfernt sind (also durch zwei oder drei Ganztonschritte voneinander getrennt sind).
Gleichwertig dazu ist:
Eine diatonische Tonleiter ist eine siebenstufige Tonleiter, die den Oktavraum in fünf Ganz- und zwei Halbtonschritte aufteilt, und zwei diatonische Tetrachorde enthält.
Im Unterschied zur Definition über Stammtöne werden keine Notennamen vorausgesetzt. Offensichtlich erfüllen die „klassischen“ diatonischen Tonleitern (Dur, Moll und die Kirchentonarten) die Bedingungen.
Erweiterte Auffassungen[Bearbeiten | Quelltext bearbeiten]
In Erweiterung dieser ursprünglichen strengen Definition werden heute manchmal auch solche Tonleitern als diatonisch bezeichnet, die lediglich die Bedingung erfüllen, die Oktave in fünf Ganz- und zwei Halbtöne zu unterteilen. Beispiele hierfür sind die akustische und die alterierte Skala.
Außerdem können nach heutigem Verständnis auch Tonleitern als diatonisch angesehen werden, die weniger als sieben Töne enthalten, wie z. B. die anhemitonisch-pentatonischen Leitern, welche den Oktavraum in drei Ganztonschritte und zwei Terzen aufteilen.[9]
Beispiele[Bearbeiten | Quelltext bearbeiten]
Die bekanntesten und wichtigsten diatonischen Tonleitern sind heute die Dur- und die (natürliche) Molltonleiter: 
mit folgender Verteilung von Ganz- und Halbtonschritten:
| C-Dur | c′ | d′ | e′ | f′ | g′ | a′ | h′ | c" | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tonschritt | Ganzton | Ganzton | Halbton | Ganzton | Ganzton | Ganzton | Halbton | |||||||||
| c-Moll | c′ | d′ | es′ | f′ | g′ | as′ | b′ | c" | ||||||||
| Tonschritt | Ganzton | Halbton | Ganzton | Ganzton | Halbton | Ganzton | Ganzton | |||||||||
Zu den diatonischen Tonleitern im engeren Sinne („klassische“ diatonische Tonleitern) gehören außerdem die Kirchentöne und die heute auf sie zurückgreifenden modalen Tonleitern.
Im weiteren Sinne (vgl. oben unter „Definition“) sind auch diese Tonleitern diatonisch:
- die melodische Molltonleiter aufwärts
- die vor allem im Jazz verwendete alterierte Skala
- die akustische Skala
- die anhemitonisch-pentatonischen Leitern
Abgrenzung[Bearbeiten | Quelltext bearbeiten]
Diese Tonleitern sind nicht diatonisch oder nicht vollständig diatonisch:
- die harmonische Molltonleiter, da sie eine übermäßige Sekunde (Hiatus) enthält
- die Zigeunertonleitern, da sie übermäßige Sekunden (Hiatus) enthalten
- die Ganztonleiter, da der letzte, zum Erreichen der Oktave benötigte Ganztonschritt in Wahrheit eine verminderte Terz (bei von c ausgehender Notation ais-c) ist
- die chromatische Tonleiter
- die Modi mit begrenzten Transpositionsmöglichkeiten von Olivier Messiaen
Diatonische Intervalle[Bearbeiten | Quelltext bearbeiten]
Diatonische Intervalle sind solche, die in einer diatonischen Tonleiter leitereigen enthalten sind. Im Einzelnen sind dies: reine Prime, Quarte, Quinte und Oktave, kleine und große Sekunden, Terzen, Sexten und Septimen. Der Tritonus ist zwar auch Bestandteil diatonischer Leitern, wird aber als übermäßige Quarte, also als chromatische Variante der reinen Quarte bestimmt und nicht zu den diatonischen Intervallen gerechnet.
Im Unterschied zu chromatischen (also übermäßigen oder verminderten) Intervallen gelten in der tonalen Musik diatonische Intervalle als unmittelbar verständlich. Für die Unterscheidung von diatonischen und chromatischen Intervallen spielt es keine Rolle, ob die beteiligten Töne Versetzungszeichen haben oder nicht. Entscheidend ist allein, ob das betreffende Intervall Bestandteil einer diatonischen Skala ist oder nicht.
Beispiele:
- Die kleine Terz c-es ist ein diatonisches Intervall, das unter anderem in c-Moll, Es-Dur oder B-Dur leitereigen vorkommt. Bei enharmonischer Umdeutung des es zum dis wird daraus ein chromatisches Intervall: die übermäßige Sekunde c-dis, die in keiner diatonischen Skala enthalten ist.
- Die kleine Sekunde c-des ist diatonisch, die übermäßige Prime c-cis ist dagegen chromatisch. Die kleine Sekunde wird auch diatonischer Halbton, die übermäßige Prime chromatischer Halbton genannt.
Die Unterscheidung zwischen chromatischen und diatonischen Intervallen ist nur bei Verwendung reiner Stimmungen akustisch real, bei der heute üblichen gleichstufigen Stimmung – ein Kompromiss in der Intonation – dagegen verschwindet der hörbare Unterschied. Er existiert dann nur noch im Notenbild, ist aber zum Verständnis musikalischer Zusammenhänge in der Dur-Moll-Tonalität unverzichtbar.
Herleitungsverfahren[Bearbeiten | Quelltext bearbeiten]

Die Bezeichnung diatonisch stellt lediglich eine Abgrenzung zur Chromatik dar; wie die Tonleitern konstruiert sind, ist damit noch nicht bestimmt. Diese können distanziell, harmonisch oder melodisch hergeleitet werden. Eine genauere engere Begriffsabgrenzung ist abhängig von der Betrachtungsweise des jeweiligen Musiktheoretikers.
Herleitung über Quintenschichtung[Bearbeiten | Quelltext bearbeiten]
Eine der möglichen Herleitungen beruht auf Quintschritten im Quintenzirkel, man spricht auch von Quintenschichtung (oder Quintschichtung). Ausgehend von C gelangt man im Quintenzirkel bei einem Schritt abwärts (gegen den Uhrzeigersinn) zu F. Aufwärts (im Uhrzeigersinn) gelangt man nacheinander zu G, D, A, E, H (siehe Bild rechts). Das sind insgesamt alle Töne der C-Dur-Tonleiter.
Diese Herleitung entspricht der pythagoreischen Stimmung (s. u.).
Herleitung über drei Dreiklänge[Bearbeiten | Quelltext bearbeiten]
Eine andere, harmonisch begründete Herleitung ist die Vereinigung von Dreiklängen auf Tonika, Subdominante (Quarte) und Dominante (Quinte). Beispielsweise ist die C-Dur Tonleiter die Vereinigung der drei Dur-Akkorde C-Dur (Tonika), F-Dur (Subdominante) und G-Dur (Dominante).
Diese Herleitung entspricht der reinen Stimmung (s. u.) bei Verwendung von reinen Dur-Akkorden (mit reiner Terz 5:4).
Herleitung über Festlegung der beiden Halbtonschritte[Bearbeiten | Quelltext bearbeiten]

Eine weitere gängige Herleitung geht von einer bestimmten Folge von Ganz- und Halbtonschritten aus, z. B. bei Dur: Ganzton – Ganzton – Halbton – Ganzton – Ganzton – Ganzton – Halbton (siehe Bild links).
Unbefriedigend bei dieser Herleitung ist die Tatsache, dass keine harmonische Begründung für die Lage der Halbtonschritte gegeben wird.
Hermann Grabners (1886–1969)[10] Definition wie auch die Definition von Johann Georg Sulzer[11] (1771) sind wesentlich ausführlicher.
Stimmungen[Bearbeiten | Quelltext bearbeiten]
In enger Beziehung zu den Herleitungsverfahren stehen die Stimmungen der siebenstufigen diatonischen Dur-Tonleiter.
Die pythagoreische Stimmung ergibt sich durch Quintenschichtung und ist die Stimmung mit den Tonstufen Q0, Q2/O, Q4/O2, Q-1O, Q1, Q3/O, Q5/O2, wobei O die Oktave und Q die Quinte bezeichnen.
Die reine Stimmung ist diejenige Stimmung, bei der die Tonstufen die Frequenzverhältnisse 1:1, 9:8, 5:4, 4:3, 3:2, 5:3, 15:8 haben.
Die gleichstufige Stimmung ist diejenige Stimmung, bei der die Tonstufen die Frequenzverhältnisse H0, H2, H4, H5, H7, H9, H11 haben, wobei H die 12. Wurzel aus 2 bezeichnet.
Geschichtliches[Bearbeiten | Quelltext bearbeiten]
Antike[Bearbeiten | Quelltext bearbeiten]
In der Musik des antiken Griechenlands traten als Tongeschlechter (wohl wegen der ausschließenden Einstimmigkeit) neben der Diatonik auch die Chromatik und die Enharmonik auf. Bei Aristoxenos sind diatonische Skalen solche, bei denen zwischen den beiden Halbtönen immer abwechselnd zwei und drei Ganztöne liegen.[12] Einige der ältesten Quellen über die Diatonik gehen auf griechische Philosophen und Mathematiker zurück. Siehe dazu auch:
- Philolaos, Abschnitt Musiktheorie
- Archytas, Abschnitt Musik
- Aristoxenos, Abschnitt Harmonik
- Euklid, Abschnitt Musiktheorie
In der Spätantike beschreibt Boëthius (um 500) die pythagoreische Tonfolge, bezeichnete aber noch oktavverwandte Töne mit verschiedenen Buchstaben.
Mittelalter[Bearbeiten | Quelltext bearbeiten]

Odo von Cluny (878 bis 942) vereinfachte die Schreibweise. Guido von Arezzo (um 1025) schrieb diese folgendermaßen.[13]
| Schreibweise nach Odo | Γ | A | B | C | D | E | F | G | a | ♭ | ♮ | c | d | e | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| heutige Schreibweise | G | A | H | c | d | e | f | g | a | b | h | c′ | d′ | e′ | … |
Es handelt sich hier um die pythagoreische Tonfolge, bei welcher der (pythagoreische) Ganzton das Frequenzverhältnis 9:8 (204 Cent) hat und der Halbton (Quarte – 2*pyth. Ganzton), auch Leimma genannt, das Frequenzverhältnis von 256:243 (90 Cent).[14][15]
Die Kirchentonarten zum Beispiel dorisch: D E F G a h c umfassten dann sieben Töne einer Oktave. Guido von Arezzo (um 1025) legte dafür die Grundlage, indem er Notenlinien und die Solmisation einführte (siehe Guidonische Hand).
Weltweite Verbreitung[Bearbeiten | Quelltext bearbeiten]
Die diatonischen Tonleitern in der Erweiterung auf zwölf Halbtönen pro Oktave setzten sich weltweit stärker durch als andere; so auch in Ägypten, Indien und China, während arabische Musik mit 24 Intervallen pro Oktave, indische mit 66 oder 22 Mikrotönen pro Oktave und pentatonische chinesische kaum im Westen zu hören ist.
Michael Schmidt-Salomon führt das mit einer evolutionär-humanistischen Begründung auf innenmusikalische Gründe zurück. Die höhere Verbreitung sei nicht die Folge von Kulturimperialismus, sondern eines Selektionsvorteils der pythagoreischen Skala, vor allem, seit das System im 17ten Jahrhundert mit der wohltemperierten, bzw. gleichstufigen Stimmung noch einmal verbessert wurde. Damit eigne sie sich besonders, um neue Stile hervorzubringen, während andere Systeme nur begrenzt ausbaufähig seien.[16]
Der Musikwissenschaftler Robert Jourdain beschreibt es folgendermaßen:
„Die Einteilung des Tonraums in zwölf Abschnitte ist offenbar genau richtig: zusätzliche Töne könnte das Gehirn nicht mehr ohne Mühe kategorisieren, und mit weniger könnte man kein differenziertes harmonisches System aufbauen.“[17]
Andere Musikwissenschaftler halten diese Vereinfachung auf 12 Halbtöne für eine grobe Missachtung der Intonation.
Ross W. Duffin[18] schreibt dazu:
„Unbeschadet, wie meisterhaft die heutigen Musiker sind, sie hören nicht mehr die schlechte große Terz der gleichstufigen Stimmung.“
Und der Cellist Pablo Casals gibt den Ratschlag:[19]
„Erschrick nicht, wenn Du eine andere Intonation als das Klavier hast. Das liegt am Klavier, das verstimmt ist. Das Klavier mit seiner gleichstufigen Stimmung ist ein Kompromiss in der Intonation.“
Diatonische Handzuginstrumente[Bearbeiten | Quelltext bearbeiten]
Der Begriff „diatonisch“ wird oft auch auf Handzuginstrumente angewendet, die auf Zug und Druck unterschiedliche Töne wiedergeben. Präziser wäre in diesem Fall „wechseltönig“, da die Wechseltönigkeit nicht diatonisch sein muss.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Zsolt Gárdonyi, Hubert Nordhoff: Harmonik. Möseler, Wolfenbüttel 2002, ISBN 3-7877-3035-4, S. 242–243.
Einzelnachweise und Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Diatonik. In: Wilibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musiklexikon. 12., völlig neubearbeitete Auflage. Sachteil: A–Z. Schott, Mainz 1967, S. 224.
- ↑ In der altgriechischen Musiktheorie wurde unter τόνος im engeren Sinne der Ganzton verstanden, deshalb διάτονος: „durch Ganztöne (gehend)“. Letzteres bezieht sich auf das diatonische Tongeschlecht bzw. den dafür maßgeblichen diatonischen Tetrachord, der das Rahmenintervall einer reinen Quarte „durch Ganztöne gehend“ auszufüllen versucht, wobei aber ein Rest in Form eines Halbtons (Diesis, später Limma genannt), übrigbleibt.
- ↑ Die Interpretation kann auch vom Verb ausgehen: von griechisch δια „durch“ und τείνω „spannen, an-, ausspannen“. Wenn man unter „Spannen“ das Aufspannen und Stimmen von Saiten einer Lyra oder Kithara versteht, so kann man διατείνω frei als „durch eine Stimmung“ bzw. „durch eine Tonart“ übersetzen.
- ↑ Tonsystem. In: Wilibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musiklexikon. 12., völlig neubearbeitete Auflage. Sachteil: A–Z. Schott, Mainz 1967, S. 970.
- ↑ Marc Honegger, Günther Massenkeil (Hrsg.): Das große Lexikon der Musik. Band 8: Štich – Zylis-Gara. Aktualisierte Sonderausgabe. Herder, Freiburg im Breisgau u. a. 1987, ISBN 3-451-20948-9, S. 148 f.
- ↑ Tonleiter. In: Wilibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musiklexikon. 12., völlig neubearbeitete Auflage. Sachteil: A–Z. Schott, Mainz 1967, S. 968.
- ↑ Zum Beispiel von Guido von Arezzo (992–1050) beschrieben.
- ↑ Im Gegensatz Brahms – Wagner wurde ein erbitterter Streit ausgetragen. Wagner behält die Diatonik im Volkstümlichen und Historischen bei, findet aber zum Beispiel im Tristan die ihm eigene chromatische Tonsprache. Die „Brahmsianer“ halten dagegen die Diatonik mit Rückgriff auf die Kirchentonarten und den Kontrapunkt bei. Die ab 1906 von Arnold Schönberg entwickelten Zwölftontechnik steht schließlich in völligem Gegensatz zur Diatonik.
- ↑ Marc Honegger, Günther Massenkeil (Hrsg.): Das große Lexikon der Musik. Band 2: C – Elmendorff. Aktualisierte Sonderausgabe. Herder, Freiburg im Breisgau u. a. 1987, ISBN 3-451-20948-9, S. 312.
- ↑ Hermann Grabner: Allgemeine Musiklehre. Bärenreiter, Kassel 2004, ISBN 3-7618-0061-4.
- ↑ Textlog: Johann Georg Sulzer: Diatonisch, gesehen 16. September 2010.
- ↑ Walter Bühler: Rechnen mit musikalischen Intervallen, Skalen und Stimmungen. PL Academic Research, 2014, ISBN 978-3-631-65059-2, §17.1.
- ↑ Mich. Hermesdorff (Hrsg.): Micrologus Guidonis de disciplina artis musicae, d. i. Kurze Abhandlung Guido’s über die Regeln der musikalischen Kunst. Grach, Trier 1876, S. 17 (Textarchiv – Internet Archive).
- ↑ Mich. Hermesdorff (Hrsg.): Micrologus Guidonis de disciplina artis musicae, d. i. Kurze Abhandlung Guido’s über die Regeln der musikalischen Kunst. Grach, Trier 1876, S. 21. Zitat: „Aus diesen Längenmaßen ergeben sich für die in der Tonreihe eingeschlossenen Intervalle folgende Verhältnisse: Kleine Secunde B-C E-F = 243:256; Große Secunde Γ-A, A-B u.s.w. 8:9; kleine Terz A-C, D-F u.s.w. = 27:32; große Terz C-E, F-a = 64:81; reine Quart Γ-C, C-F u.s.w. = 3:4; reine Quinte Γ-D, C-G u.s.w. = 2:3; kleine Sexte E-C = 81:128; große Sexte Γ-E, C-a u.s.w. = 16:27; kleine Septime Γ-F =9:16; große Septime C-♮ =128:243; Oktav Γ-G = 1:2; große Quart F-♮ =512: 729; kleine Quinte (als Umkehrung des Tritonus) = 729:1024.“
- ↑ Der Ton Γ – eine Oktave unter G – diente zur Bestimmung der Quarte von Γ nach C. Damit umging man die Konstruktion des praktisch unmöglich auszuführenden Verhältnisses c:A = 32:27 oder gar c:H = 256:243. (Textarchiv – Internet Archive).
- ↑ Michael Schmidt-Salomon: Hoffnung Mensch. Eine bessere Welt ist möglich. Piper Verlag, München 2014, S. 199–200.
- ↑ Robert Jourdain: Das wohltemperierte Gehirn: Wie Musik im Kopf entsteht und wirkt. Spektrum Verlag, Heidelberg 1998, S. 110.
- ↑ Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You Should Care). s.30 W. W. Norton & Company, New York NY 2007, ISBN 978-0-393-06227-4 (Exzerpt (Memento des vom 16. März 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.).
- ↑ The Way They Play (1972).