Prinzip von Inklusion und Exklusion
Das Prinzip von Inklusion und Exklusion (auch Prinzip der Einschließung und Ausschließung oder Einschluss-Ausschluss-Verfahren) ist eine zur Bestimmung der Mächtigkeit einer Menge hilfreiche Technik. Sie findet vor allem in der Kombinatorik, der Zahlentheorie und der Stochastik Anwendung.
Das Prinzip drückt dazu die Kardinalität einer Ursprungsmenge durch die Kardinalitäten ihrer Teilmengen aus. Diese sind in aller Regel einfacher zu bestimmen. Namensgebend ist dabei das Vorgehen, bei dem zunächst durch die Summe der Größen nicht notwendigerweise disjunkter Teilmengen die Größe von von oben abgeschätzt wird (Inklusion), anschließend jedoch durch die Subtraktion der Größe des gemeinsamen Schnittes der Teilmengen dies wieder zu korrigieren versucht wird (Exklusion).
Das Prinzip[Bearbeiten | Quelltext bearbeiten]
Es ist ein bekanntes Ergebnis, dass für je zwei endliche Mengen und
gilt. Hierbei kann man bereits das Prinzip von Inklusion und Exklusion erkennen. Durch wird zunächst die Kardinalität von von oben abgeschätzt. Diese zu hohe Zahl wird anschließend durch die Subtraktion von korrigiert. Zweck dieser Korrektur ist es, diejenigen Elemente einmal wieder abzuziehen, die sowohl in als auch in enthalten sind und somit zunächst doppelt gezählt wurden.
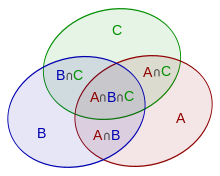
Anhand der nebenstehenden Abbildung lässt sich erkennen, dass eine Verallgemeinerung auf drei endliche Mengen
ergibt.
Im Allgemeinen wollen wir die Kardinalität der Vereinigung von endlichen Mengen
bestimmen. Als erste Näherung erhalten wir durch Inklusion die Summe der Kardinalitäten der . Diese Summe kann jedoch zu groß sein, da wir Elemente aus dem Schnitt zweier Mengen mehrfach zählen würden, es gilt also
Um dies zu korrigieren, können wir nun durch Exklusion die Summe der Kardinalitäten der Schnittmengen aller Mengenpaare wieder abziehen. Dann gilt
Denn Elemente des Schnittes dreier Mengen würden – obwohl nur zweimal zu häufig bei der Inklusion mitgezählt – durch , durch und durch dreimal wieder abgezogen. Dies nun durch Inklusion, also durch Addition der Summe der Größe aller Schnitte aus drei Mengen, zu korrigieren, ergibt
Darauf folgt durch Exklusion
und so weiter, wobei beispielsweise bedeutet, dass über alle geordneten Tripel summiert wird, die den Ungleichungen genügen.
Satz[Bearbeiten | Quelltext bearbeiten]
Es lässt sich folgende allgemeine Aussage beweisen.
Gegeben sei eine endliche Menge , die sich als Vereinigung von Teilmengen schreiben lässt, d. h. . Es bezeichne im Folgenden zu einer Indexmenge die Menge den Schnitt über alle durch die Elemente der Indexmenge bezeichneten Teilmengen, also:
- mit dem Spezialfall
Dann gilt:
oder gleichwertig auch
Mit anderen Worten: Betrachtet man alle möglichen Schnitte (außer dem leeren Schnitt ), so ist die Kardinalität von gleich der Summe der Kardinalität aller Schnitte einer ungeraden Anzahl an Teilmengen (Inklusion) minus der Summe der Kardinalität aller Schnitte einer geraden Anzahl an Teilmengen (Exklusion), formal:
Anwendung[Bearbeiten | Quelltext bearbeiten]
Eine Anwendung des Prinzips liefert die Siebformel von Poincaré und Sylvester, auch Additionssatz für Wahrscheinlichkeiten genannt:
Für die Wahrscheinlichkeit von beliebigen Ereignissen aus einem Wahrscheinlichkeitsraum gilt:
Wegen der Additivität von Maßen lässt sich der oben angegebene heuristische Beweis für das Prinzip von Inklusion und Exklusion, der mit Mitteln der elementaren Mengentheorie geführt wurde, direkt auf Wahrscheinlichkeiten übertragen.
Beispielsweise gilt für drei Ereignisse , und stets
- .
Allgemein gilt diese Aussage auch schon für endliche Inhalte auf Ringen.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Beim vorweihnachtlichen Brauch des Wichtelns beschenkt sich eine Gruppe gegenseitig. Jeder beschenkt genau eine Person und wird wiederum von genau einer Person beschenkt. Dabei wird per Los zufällig festgelegt, wer welches Geschenk erhält. Idealerweise sollte jeder das Geschenk eines anderen erhalten. Es kann jedoch passieren, dass jemand zufällig sein eigenes Geschenk bekommt. Für die betreffende Person wäre es mit der Überraschung vorbei. Doch wie wahrscheinlich ist dieser Fall bei einer Gruppe von Personen?
Mathematisch ausgedrückt möchte man die Wahrscheinlichkeit des Ereignisses A := „Mindestens eine Person erhält ihr eigenes Geschenk“ ermitteln. Dies ist äquivalent dazu, dass mindestens eines der Ereignisse Ai := „Person i erhält ihr eigenes Geschenk“ für zutrifft, wobei die Anzahl Personen ist, die am Wichteln teilnimmt. Der rechte Term der Siebformel
kann vereinfacht werden zu
-
- ,
da in diesem Beispiel die Wahrscheinlichkeiten aller Schnittmengen mit derselben Anzahl an Teilmengen gleich sind. Die Wahrscheinlichkeit, dass bestimmte Personen jeweils ihre eigenen Geschenke ziehen, beträgt
- .
Mit Hilfe der Definition des Binomialkoeffizienten erhält man somit
-
- .
Nach dem Kürzen der Brüche ergibt sich
- .
Mit der Summenschreibweise lässt sich das verkürzt als ausdrücken.
Bei großen Gruppen müssen ziemlich viele Summanden addiert werden und die Fakultät wird schnell extrem groß. In diesem Fall ist es zweckmäßig, den Grenzwert dieser Summe für zu bilden:
Bei der Reihe handelt es sich um die Auswertung der Taylorreihe mit Entwicklungsstelle der natürlichen Exponentialfunktion an der Stelle , weshalb sich die Lösung auf insgesamt vereinfacht. Dieser Wert kann als Näherung für großes betrachtet werden. In großen Gruppen beträgt die Wahrscheinlichkeit demnach etwa , dass mindestens eine Person ihr eigenes Geschenk erhält.[1][2]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. Springer Spektrum, 10. Auflage, Wiesbaden 2016, S. 70–76.
- Klaus Dohmen: Improved Bonferroni Inequalities via Abstract Tubes – Inequalities and Identities of Inclusion-Exclusion Type. Springer-Verlag, 2003, ISBN 3-540-20025-8.
- Stasys Jukna: Extremal Combinatorics. Springer, Mai 2001, ISBN 3-540-66313-4.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Sinngemäß in leicht anderer Einkleidung in: Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. Springer Spektrum, 1. Auflage, Wiesbaden 1997, S. 74–77.
- ↑ Stefan Bartz: Selbst-Bewichtelungen in 2 von 3 Spielen. In: Stochastik in der Schule. Nr. 33, 2013 (stefanbartz.de [PDF; 684 kB]).





















































