Problem der 100 Gefangenen

Das Problem der 100 Gefangenen ist ein mathematisches Problem aus der Wahrscheinlichkeitstheorie und Kombinatorik. Bei diesem Problem muss jeder von 100 durchnummerierten Gefangenen zum Überleben aller seine eigene Nummer in einer von 100 Schubladen wiederfinden, wobei jeder Gefangene nur 50 der Schubladen öffnen und mit den anderen Gefangenen nicht kommunizieren darf. In dieser zunächst aussichtslos erscheinenden Situation gibt es dennoch eine Strategie, die den Gefangenen eine gute Überlebenschance gibt. Das Problem wurde erstmals 2003 vom dänischen Informatiker Peter Bro Miltersen vorgestellt.
Problemstellung
[Bearbeiten | Quelltext bearbeiten]Für das Problem der 100 Gefangenen finden sich in der Literatur unterschiedliche Darstellungen. Die folgende Formulierung des Problems basiert auf einer Beschreibung von Philippe Flajolet und Robert Sedgewick:[1]
- „Der Leiter eines Gefängnisses gibt 100 zum Tode verurteilten Gefangenen mit den Nummern von 1 bis 100 eine letzte Chance. In einem Raum befindet sich ein Schrank mit 100 Schubladen. Der Gefängnisleiter legt in jede Schublade die Nummer genau eines Gefangenen in zufälliger Reihenfolge und schließt die Schubladen daraufhin. Die Gefangenen betreten den Raum der Reihe nach. Jeder Gefangene darf 50 Schubladen in einer beliebigen Reihenfolge öffnen und muss sie danach mit ihrem Inhalt wieder schließen. Finden dabei alle Gefangenen ihre eigene Nummer in einer der Schubladen, werden die Gefangenen begnadigt. Findet irgendein Gefangener seine Nummer nicht, müssen alle Gefangenen sterben. Bevor der erste Gefangene den Raum betritt, dürfen sich die Gefangenen beraten, danach ist jedoch keinerlei Kommunikation mehr möglich. Was ist für die Gefangenen die beste Strategie?“
Wählt jeder Gefangene seine 50 Schubladen zufällig aus, dann beträgt die Wahrscheinlichkeit, dass ein einzelner Gefangener seine Nummer findet, 50 Prozent. Die Wahrscheinlichkeit, dass alle Gefangenen ihre Nummern finden, ist dann gleich dem Produkt der Einzelwahrscheinlichkeiten und somit 0,5100 ≈ 10−30,1 ≈ 8 · 10−31 = 0,0000000000000000000000000000008, d. h. mit weniger als 1 : 1 Quintillion verschwindend gering. Die Situation erscheint aussichtslos für die Gefangenen.
Lösung
[Bearbeiten | Quelltext bearbeiten]Strategie
[Bearbeiten | Quelltext bearbeiten]Es gibt jedoch eine Strategie, mit der die Gefangenen eine Überlebenswahrscheinlichkeit von etwas mehr als 30 % erhalten. Der Schlüssel zum Erfolg liegt darin, dass die Gefangenen nicht vorab entscheiden müssen, welche Schubladen sie öffnen wollen. Jeder Gefangene kann sich bei der Entscheidung, welche Schublade er als Nächstes öffnet, auf die Informationen stützen, die er aus den von ihm bereits geöffneten Schubladen erhalten hat. Eine weitere wichtige Beobachtung ist, dass dabei der Erfolg eines Gefangenen nicht unabhängig vom Erfolg der anderen Gefangenen ist.[2]
Zunächst werden die Schubladen von den Gefangenen gedanklich mit den Zahlen von 1 bis 100 durchnummeriert, zum Beispiel zeilenweise von links oben nach rechts unten. Die Strategie lautet nun wie folgt:[3]
- Jeder Gefangene öffnet als erste die Schublade, die mit seiner eigenen Nummer gedanklich nummeriert ist.
- Befindet sich seine Nummer in dieser Schublade, dann ist er mit der Suche fertig und war erfolgreich.
- Andernfalls befindet sich in der Schublade die Nummer eines anderen Gefangenen und er öffnet als nächste die Schublade mit dieser Nummer.
- Der Gefangene wiederholt die Schritte 2 und 3 so lange, bis er seine eigene Nummer gefunden hat oder bis er 50 Schubladen geöffnet hat.
Ohne die Beschränkung auf 50 Schubladen würde sich bei diesem Vorgehen in jedem Fall ein Zyklus von Nummern ergeben, der mit der Nummer des Gefangenen beginnt und endet. Falls dieser Zyklus aus bis zu 50 Nummern besteht, war der Gefangene erfolgreich; andernfalls ist er gescheitert.
Beispiele
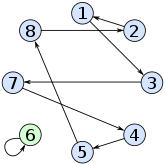
[Bearbeiten | Quelltext bearbeiten]Dass diese Strategie erfolgversprechend ist, soll an folgendem Beispiel mit acht Gefangenen und Schubladen, wobei jeder Gefangene vier Schubladen öffnen darf, illustriert werden. Der Gefängnisleiter habe die Nummern der Gefangenen wie folgt auf die Schubladen verteilt:
| Nummer der Schublade | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nummer des Gefangenen | 7 | 4 | 6 | 8 | 1 | 3 | 5 | 2 |
Die Gefangenen handeln nun wie folgt:
- Der Gefangene 1 öffnet Schublade 1 und findet dort die Nummer 7. Daraufhin öffnet er Schublade 7 und findet dort die Nummer 5. Nun öffnet er Schublade 5, findet dort seine eigene Nummer 1 und ist somit erfolgreich.
- Der Gefangene 2 öffnet die Schubladen 2, 4 und 8 in dieser Reihenfolge, wobei er in Schublade 8 seine eigene Nummer 2 findet.
- Der Gefangene 3 öffnet die Schubladen 3 und 6, wo er bereits seine eigene Nummer findet.
- Der Gefangene 4 öffnet die Schubladen 4, 8 und 2, wo er dann seine eigene Nummer findet. Dies kann auch aus den Informationen, die der zweite Gefangene erhalten hat, abgeleitet werden.
- Dass auch die Gefangenen 5 bis 8 ihre Nummern finden werden, kann ebenfalls aus den Informationen der ersten drei Gefangenen abgeleitet werden.
Die Gefangenen werden in diesem Fall also erfolgreich alle ihre Nummern finden. Allerdings ist dies nicht immer der Fall. Als zweites Beispiel habe der Gefängnisleiter die Nummern nun wie folgt verteilt:
| Nummer der Schublade | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nummer des Gefangenen | 3 | 1 | 7 | 5 | 8 | 6 | 4 | 2 |
In diesem Fall öffnet der Gefangene 1 der Reihe nach die Schubladen 1, 3, 7 und 4, wo er erfolglos abbrechen muss. Bis auf den Gefangenen 6, der direkt seine Nummer findet, wären auch alle anderen Gefangenen erfolglos.
Permutationsdarstellung
[Bearbeiten | Quelltext bearbeiten]Die von dem Gefängnisleiter vorgenommene zufällige Zuordnung von Gefangenen zu Schubladen kann mathematisch als Permutation der Zahlen von 1 bis 100 beschrieben werden. Eine solche Permutation ist eine eindeutig umkehrbare Abbildung der Menge der natürlichen Zahlen von 1 bis 100 auf sich selbst. Eine Folge von Zahlen, die durch wiederholte Anwendung einer Permutation entsteht und am Ende zur Ausgangszahl zurückkehrt, heißt Zyklus der Permutation. Jede Permutation zerfällt in disjunkte Zyklen bestehend aus unterschiedlichen Zahlen und kann durch ihren Zyklentyp beschrieben werden. Die erste Beispielpermutation des vorangegangenen Abschnitts kann in Zyklenschreibweise durch
dargestellt werden und besteht damit aus zwei Zyklen der Länge drei und einem Zyklus der Länge zwei. Die zweite Beispielpermutation hat die Darstellung
und besteht aus einem Zyklus der Länge sieben und einem der Länge eins. Die Zyklendarstellung ist dabei nicht eindeutig, denn ein Zyklus der Länge kann durch Wahl jeweils einer anderen Startzahl auf verschiedene Weisen geschrieben werden. Jeder Gefangene folgt beim Öffnen der Schubladen nun einem Zyklus, der mit seiner eigenen Nummer endet. Bei acht Gefangenen ist diese Zyklusfolgestrategie für eine beliebige Permutation genau dann erfolgreich, wenn die Länge des längsten Zyklus der Permutation höchstens vier ist. Besitzt die Permutation nämlich einen Zyklus der Länge fünf oder größer, dann werden alle Gefangenen, deren Nummern in diesem Zyklus liegen, nach vier Schritten noch nicht bei ihrer eigenen Nummer angelangt sein.
Erfolgswahrscheinlichkeit
[Bearbeiten | Quelltext bearbeiten]
Übertragen auf das ursprüngliche Problem der 100 Gefangenen werden diese mit ihrer Strategie genau dann erfolgreich sein, wenn der längste Zyklus der Permutation höchstens die Länge 50 besitzt. Die Wahrscheinlichkeit, dass die Gefangenen überleben, ist somit gleich der Wahrscheinlichkeit, dass eine zufällige Permutation der Zahlen von 1 bis 100 keinen Zyklus mit einer Länge größer als 50 enthält. Diese Wahrscheinlichkeit wird im Folgenden ermittelt.
Zunächst kann eine Permutation der Zahlen von 1 bis 100 maximal einen Zyklus mit einer Länge besitzen. Dabei gibt es genau Möglichkeiten, die Zahlen eines solchen Zyklus auszuwählen (siehe Kombination ohne Wiederholung). Diese Zahlen lassen sich innerhalb des Zyklus auf Weisen anordnen (siehe Permutation ohne Wiederholung), denn es gibt Möglichkeiten, die Startzahl des Zyklus auszuwählen. Die verbleibenden Zahlen können schließlich auf Arten angeordnet werden. Damit ist die Anzahl der Permutationen der Zahlen von 1 bis 100 mit einem Zyklus der Länge gleich
- .

Die Wahrscheinlichkeit, dass eine (gleichverteilt) zufällige Permutation keinen Zyklus mit einer Länge größer als 50 aufweist, ist mit der Formel für die Gegenwahrscheinlichkeit und der Laplace-Formel demnach
- ,
wobei die -te harmonische Zahl ist. Die Wahrscheinlichkeit, dass die Gefangenen überleben, beträgt mit der Zyklusfolgestrategie demnach erstaunliche 31 %.[3]
Grenzwertbetrachtung
[Bearbeiten | Quelltext bearbeiten]
Werden allgemein statt 100 Gefangenen Gefangene betrachtet, wobei eine beliebige natürliche Zahl ist, dann beträgt die Überlebenswahrscheinlichkeit mit der Zyklusfolgestrategie
- .
Mit der Euler-Mascheroni-Konstante gilt nun für
- ,
wodurch sich eine asymptotische Überlebenswahrscheinlichkeit von
ergibt. Da die Folge der Wahrscheinlichkeiten monoton fallend ist, überleben die Gefangenen mit der Zyklusfolgestrategie bei einer beliebigen Anzahl von Gefangenen in mehr als 30 % der Fälle.[3]
Optimalität
[Bearbeiten | Quelltext bearbeiten]Eugene Curtin und Max Warshauer gaben 2006 einen Beweis für die Optimalität der Zyklusfolgestrategie an. Der Beweis basiert auf der Herstellung einer Äquivalenz zu einem verwandten Problem, bei dem sich alle Gefangenen in dem Raum aufhalten und die Auswahl der Schubladen beobachten dürfen. Diese Äquivalenz beruht auf einer Korrespondenz zwischen der (normalisierten) Zyklenschreibweise und der Tupeldarstellung von Permutationen. In dem zweiten Problem ist die Erfolgswahrscheinlichkeit unabhängig von der gewählten Strategie und gleich der Erfolgswahrscheinlichkeit beim Ausgangsproblem mit der Zyklusfolgestrategie. Nachdem eine beliebige Strategie beim Ausgangsproblem auch in dem zweiten Problem eingesetzt werden kann, dort aber keine höhere Erfolgswahrscheinlichkeit besitzt, muss die Zyklusfolgestrategie optimal sein.[2]
Geschichte
[Bearbeiten | Quelltext bearbeiten]Das Problem der 100 Gefangenen wurde erstmals 2003 von dem dänischen Informatiker Peter Bro Miltersen betrachtet und mit Anna Gál in einem Konferenzbeitrag zum 30. International Colloquium on Automata, Languages and Programming (ICALP) veröffentlicht.[4] In ihrer Version färbt Spieler A (der Gefängnisleiter) Zettel mit den Namen der Spieler von Team B (den Gefangenen) rot oder blau und steckt diese in jeweils einen Kasten. Jeder Spieler von Team B muss, damit das Team gewinnt, die Farbe seines Zettels korrekt erraten, nachdem er die Hälfte der Kästen geöffnet hat. Anfänglich nahm Miltersen an, dass die Gewinnwahrscheinlichkeit mit der Anzahl der Spieler sehr schnell nach null strebt. Sven Skyum, ein Kollege Miltersens an der Universität Aarhus, machte ihn jedoch auf die Zyklusfolgestrategie aufmerksam. Diese Strategie zu finden, wurde in dem Konferenzbeitrag als Übungsaufgabe offengelassen. Der Beitrag wurde mit dem Best Paper Award ausgezeichnet.[2]
Das Problem erschien im Frühjahr 2004 in der Puzzlekolumne von Joe Buhler und Elwyn Berlekamp in der Zeitschrift The Emissary des Mathematical Sciences Research Institute, wobei Kästen durch Festspeicher und farbige Zettel durch vorzeichenbehaftete Zahlen ersetzt wurden. Die Autoren stellten dabei fest, dass die Gewinnwahrscheinlichkeit auch in dem Fall, dass die Teammitglieder während der Zyklusfolge ihre eigene Nummer nicht finden, erhöht werden kann. Wird in diesem Fall als Antwort das Produkt aller gefundenen Vorzeichen gegeben und ist die Länge des längsten Zyklus um eins größer als die Hälfte der (geraden) Anzahl der Spieler, dann raten die Teammitglieder, die sich in diesem Zyklus wiederfinden, entweder alle richtig oder alle falsch. Auch wenn diese Erweiterung der Strategie eine sichtbare Verbesserung bei einer kleinen Anzahl von Spielern ergibt, wird sie vernachlässigbar, wenn die Zahl der Spieler groß wird.[5]
In der Folgezeit fand das Problem Einzug in die mathematische Fachliteratur, wo es auf unterschiedliche Weise ausgekleidet wurde, zum Beispiel mit verdeckten Karten auf einem Tisch[6] oder Brieftaschen in Schließfächern (locker puzzle).[2] In der Form eines Gefangenenproblems wurde es dann 2006 von Christoph Pöppe in der Zeitschrift Spektrum der Wissenschaft und von Peter Winkler im College Mathematics Journal gestellt.[7][8] Mit leichten Abwandlungen übernahmen es in dieser Form unter anderem Philippe Flajolet, Robert Sedgewick und Richard P. Stanley in ihre Lehrbücher zur Kombinatorik.[1][3]
Varianten
[Bearbeiten | Quelltext bearbeiten]Leere Kästen
[Bearbeiten | Quelltext bearbeiten]Gál und Miltersen betrachteten in ihrem Konferenzbeitrag zunächst den Fall, dass die Anzahl der Kästen doppelt so groß wie die Anzahl der Teammitglieder ist, wobei die Hälfte der Kästen leer ist. Dies ist ein schwierigeres Problem, da leere Kästen nirgendwohin weiterleiten und die Zyklusfolgestrategie somit hier nicht eingesetzt werden kann. Es ist eine offene Frage, ob in diesem Fall die Gewinnwahrscheinlichkeit für eine wachsende Zahl von Teammitgliedern nach null strebt.[4]
Navin Goyal und Michael Saks entwickelten 2005 basierend auf der Zyklusfolgestrategie eine Strategie für Team B in einer allgemeineren Problemstellung, bei dem sowohl der Anteil leerer Kästen als auch der Anteil der Kästen, die jedes Teammitglied öffnen darf, variieren. Die Gewinnwahrscheinlichkeit strebt in diesem Fall mit wachsender Zahl von Spielern immer noch gegen null, allerdings weniger schnell als von Gál und Miltersen vermutet. Wird die Zahl der Spieler und der Anteil zu öffnender Kästen festgelassen, bleibt die Gewinnwahrscheinlichkeit echt größer als null, wenn weitere leere Kästen hinzugefügt werden.[9]
David Avis und Anne Broadbent betrachteten 2009 eine quanteninformatische Variante, bei der Team B mit Sicherheit gewinnt.[10]
Der böswillige Gefängnisleiter
[Bearbeiten | Quelltext bearbeiten]In dem Fall, dass der Gefängnisleiter die Nummern der Gefangenen nicht in zufälliger Reihenfolge in die Schubladen legen muss, kann er in Kenntnis der Nummerierung der Schubladen die Strategie der Gefangenen aushebeln. Hierzu muss er lediglich sicherstellen, dass seine Zuordnung der Nummern auf die Schubladen eine Permutation mit einem Zyklus der Länge größer als 50 darstellt. Die Gefangenen können jedoch ihre ursprüngliche Gewinnwahrscheinlichkeit wiederherstellen, indem sie ihre Nummerierung der Schubladen zufällig vornehmen.[11]
Ziegenproblem
[Bearbeiten | Quelltext bearbeiten]Adam S. Landsberg schlug 2009 folgende vereinfachte Variante des Problems vor, die sich an dem bekannten Ziegenproblem (Monty-Hall-Problem) orientiert:[12]
- „Hinter drei verschlossenen Türen befinden sich zufällig verteilt ein Auto, die Autoschlüssel und eine Ziege. Es gibt zwei Spieler: der erste Spieler muss das Auto finden, der zweite Spieler die Autoschlüssel. Nur wenn beide Spieler erfolgreich sind, dürfen sie mit dem Auto nach Hause fahren. Zunächst betritt der erste Spieler den Raum und darf nacheinander zwei der drei Türen öffnen. Ist er erfolgreich, werden die Türen wieder geschlossen und der zweite Spieler betritt den Raum. Der zweite Spieler darf ebenfalls zwei der drei Türen öffnen, kann allerdings in keiner Weise mit dem ersten Spieler kommunizieren. Wie groß ist die Gewinnwahrscheinlichkeit, wenn beide Spieler optimal handeln?“
Wählen die beiden Spieler die Türen zufällig aus, dann beträgt die Gewinnwahrscheinlichkeit lediglich 4/9 (etwa 44 %). Die optimale Strategie lautet allerdings wie folgt:
- Spieler 1 öffnet erst Tür 1. Befindet sich das Auto darin, ist er erfolgreich. Befinden sich die Schlüssel darin, öffnet er als nächstes Tür 2, ansonsten Tür 3.
- Spieler 2 öffnet erst Tür 2. Befinden sich die Schlüssel darin, ist er erfolgreich. Befindet sich die Ziege darin, öffnet er als nächstes Tür 3, ansonsten Tür 1.
Bei den sechs möglichen Verteilungen von Auto, Schlüssel und Ziege auf die drei Türen öffnen die Spieler dann die folgenden Türen (ist ein Feld grün hinterlegt, dann war der jeweilige Spieler erfolgreich):
| Auto Schlüssel Ziege |
Auto Ziege Schlüssel |
Schlüssel Auto Ziege |
Schlüssel Ziege Auto |
Ziege Auto Schlüssel |
Ziege Schlüssel Auto | |
| Spieler 1 | Tür 1: Auto | Tür 1: Auto | Tür 1: Schlüssel Tür 2: Auto |
Tür 1: Schlüssel Tür 2: Ziege |
Tür 1: Ziege Tür 3: Schlüssel |
Tür 1: Ziege Tür 3: Auto |
| Spieler 2 | Tür 2: Schlüssel | Tür 2: Ziege Tür 3: Schlüssel |
Tür 2: Auto Tür 1: Schlüssel |
(Tür 2: Ziege) (Tür 3: Auto) |
(Tür 2: Auto) (Tür 1: Ziege) |
Tür 2: Schlüssel |
Der Erfolg der Strategie besteht offenbar darin, eine Korrelation zwischen den Erfolgen beziehungsweise Misserfolgen der beiden Spieler herzustellen. Die Gewinnwahrscheinlichkeit beträgt in diesem Fall 2/3 und ist optimal, da bereits der erste Spieler keine größere Erfolgswahrscheinlichkeit besitzt.[12] Eine weitere Variante besteht darin, drei Preise hinter den drei Türen zu verstecken und drei Spieler unabhängig voneinander jeweils einen anderen vorab bestimmten Preis mit zwei Versuchen finden zu lassen. Auch hier beträgt die Gewinnwahrscheinlichkeit bei optimaler Strategie 2/3.[13]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics. Cambridge University Press, 2009, ISBN 978-1-139-47716-1.
- Richard P. Stanley: Algebraic Combinatorics: Walks, Trees, Tableaux, and More (= Undergraduate Texts in Mathematics). Springer, 2013, ISBN 978-1-4614-6998-8.
- Peter Winkler: Mathematical Mind-Benders. Taylor and Francis, 2007, ISBN 978-1-56881-336-3.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Video bei YouTube (17′11″)
- 100 Gefangene – Ein stochastisches Problem. ( vom 16. März 2016 im Internet Archive). 18. April 2009.
- Rob Heaton: Mathematicians hate civil liberties – 100 prisoners and 100 boxes. 13. Januar 2014 (englisch).
- Oliver Nash: Pity the prisoners. ( vom 18. Januar 2010 im Internet Archive). 12. Dezember 2009 (englisch).
- Jamie Mulholland: Prisoners Names in Boxes. ( vom 4. März 2016 im Internet Archive). 2011 (PDF; 204 kB; englisch).
- MinutePhysics: An Impossible Bet auf YouTube und Solution to The Impossible Bet auf YouTube. 8. Dezember 2014 (englisch).
- Edmund Weitz (HAW Hamburg): Das Problem der 100 Gefangenen auf YouTube. 21. April 2018.
- Matt Parker (standupmaths) und Alex Bellos: The unbelievable solution to the 100 prisoner puzzle auf YouTube. 4. November 2019 (englisch).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ a b Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics. Cambridge University Press, 2009, S. 124.
- ↑ a b c d Eugene Curtin, Max Warshauer: The locker puzzle. In: Mathematical Intelligencer. Nr. 28, 2006, S. 28–31, doi:10.1007/BF02986999.
- ↑ a b c d Richard P. Stanley: Algebraic Combinatorics: Walks, Trees, Tableaux, and More. Springer, 2013, S. 187–189.
- ↑ a b Anna Gál, Peter Bro Miltersen: The cell probe complexity of succinct data structures. In: Proceedings 30th International Colloquium on Automata, Languages and Programming (ICALP). 2003, S. 332–344.
- ↑ Joe Buhler, Elwyn Berlekamp: Puzzles Column. In: The Emissary. Spring. Mathematical Sciences Research Institute, 2004, S. 3 (msri.org).
- ↑ Richard E. Blahut: Cryptography and Secure Communication. Cambridge University Press, 2014, S. 29–30.
- ↑ Christoph Pöppe: Freiheit für die Kombinatoriker. Mathematische Unterhaltungen. In: Spektrum der Wissenschaft. Band 6, 2006, S. 106–108 (spektrum.de).
- ↑ Peter Winkler: Names in Boxes Puzzle. In: College Mathematics Journal. Band 37, Nr. 4, 2006, S. 260, 285, 289.
- ↑ Navin Goyal, Michael Saks: A parallel search game. In: Random Structures & Algorithms. Band 27, Nr. 2, 2005, S. 227–234.
- ↑ David Avis, Anne Broadbent: The quantum locker puzzle. In: Third International Conference on Quantum, Nano and Micro Technologies ICQNM ’09. 2009, S. 63–66.
- ↑ Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics. Cambridge University Press, 2009, S. 177.
- ↑ a b Adam S. Landsberg: The Return of Monty Hall. In: Mathematical Intelligencer. Band 31, Nr. 2, 2009, doi:10.1007/s00283-008-9016-8.
- ↑ Eric Grundwald: Re: The Locker Puzzle. In: Mathematical Intelligencer. Band 32, Nr. 2, 2010, doi:10.1007/s00283-009-9107-1.