Filter (Elektrotechnik)
Als Filter (in der Fachsprache zumeist das/ein Filter[1]) werden in der Elektrotechnik und Nachrichtentechnik Schaltungen bezeichnet, die ein elektrisches Signal abhängig von der Frequenz in der Amplitude und in der Phasenlage verändern. Dadurch können unerwünschte Signalanteile abgeschwächt oder unterdrückt werden.


Klassifizierung und Anwendungen
[Bearbeiten | Quelltext bearbeiten]Filter lassen sich nach mehreren Kriterien klassifizieren, zum Beispiel nach ihrer Komplexität, ihrem Frequenzgang, den verwendeten Bauelementen, der Schaltungsstruktur, der verwendeten Berechnungsmethode, der Trennschärfe bzw. Steilheit im Sperrbereich und der Phasenverschiebung.
Filter im klassischen Sinne, wie Tief- oder Hochpass, verändern den Frequenzgang. Sie werden auch Siebschaltungen genannt. Schaltungen und Verfahren, die komplexere Eigenschaften wie Phasenlage, Impedanz und Rauschanteile verändern, werden ebenfalls unter dem Begriff Filter zusammengefasst. In der Tontechnik werden digitale und analoge Frequenzfilter (Filter) auch als Equalizer (kurz EQ) bezeichnet und als Soundeffekte eingesetzt. Dazu gehören auch Präsenz-, Absenz-, Bandpass-, Hochpass- und Tiefpassfilter.
Bekannte Anwendungen sind:
- Hörfunk/Rundfunk: Auswahl einer bestimmten Sendefrequenz um einen Sender zu empfangen. Dabei wird nur die eingestellte Frequenz empfangen. Alle anderen Frequenzen werden ausgefiltert.
- Lautsprecherweiche: Die unterschiedlichen Frequenzen für Höhen, Tiefen und Mittelton werden aufgesplittet und an die entsprechenden Lautsprecher verteilt.
- Netzfilter: Sie unterdrücken Knackser beim Einschalten anderer Verbraucher und sonstige Störungen
- DSL-Splitter, die die niederfrequenten Telefonsignale und DSL trennen
- Messwertverarbeitung im Maschinenbau, der Automobilindustrie, Luft- und Raumfahrttechnik
- Sallen-Key-Filter, damit lassen sich einfache Schaltungen realisieren.
Geschichte
[Bearbeiten | Quelltext bearbeiten]Die Grundlagen der Theorie der elektrischen Filter wurden schon 1915 von dem deutschen Nachrichtentechniker Karl Willy Wagner und dem amerikanischen Nachrichtentechniker George Ashley Campbell entwickelt.
Frequenzfilter
[Bearbeiten | Quelltext bearbeiten]Frequenzfilter sind Schaltungen („Netzwerke“ genannt) mit vorgegebenem frequenzabhängigem Übertragungsverhalten (Frequenzgang), die bestimmte Frequenzbereiche des Eingangssignals unterdrücken (Sperrbereich) und/oder andere Bereiche bevorzugt übertragen; siehe Durchlassbereich.
Kenngrößen
[Bearbeiten | Quelltext bearbeiten]Alle Merkmale eines linearen Filters werden durch den Frequenzgang oder allgemein durch die Übertragungsfunktion beschrieben. Wesentlich ist dabei die Kennfrequenz fc (Center Frequency) und bei Bandpässen/sperren die Filtergüte Q. fc ist in den meisten Fällen nicht gleich f3, der Grenzfrequenz, bei der die Amplitude um 3 dB gesunken ist. Dies wird in Tietze/Schenk (siehe Literatur) ausführlich behandelt.
Übertragungsfunktionen von Filtern
[Bearbeiten | Quelltext bearbeiten]Unabhängig von der konkreten Realisierung des Filters (ob analog oder zeitdiskret bzw. digital) lässt sich die Funktionsweise eines Filters durch seine Übertragungsfunktion beschreiben. Diese bestimmt, wie das Eingangssignal in der Amplitude und im Phasenwinkel verändert wird.
Übertragungsfunktionen analoger Filter
[Bearbeiten | Quelltext bearbeiten]Die Filter sollten beim Entwurf anhand der gewünschten Übertragungsfunktion konzipiert werden. Bei der Wahl der Übertragungsfunktion mehrpoliger analoger Filter haben sich je nach gewünschter Filtercharakteristik verschiedene optimierte Frequenzgänge bei analogen Filtern bewährt:
| Filtercharakteristik | Eigenschaften | Vorteile | Nachteile |
|---|---|---|---|
| Butterworth-Filter | Maximal flacher Verlauf des Betragsfrequenzganges im Durchlassbereich, Dämpfung im Sperrbereich monoton verlaufend | Gutes Amplitudenverhalten im Durchlass- und Sperrbereich | Geringe Flankensteilheit im Übergangsbereich |
| Legendre-Filter | Flacher Verlauf des Betragsfrequenzganges im Durchlassbereich, Dämpfung im Sperrbereich monoton verlaufend | Kompromiss zwischen Butterworth-Filter und Tschebyscheff-Filter | |
| Tschebyscheff-Filter | Welligkeit (Ripple) im Durchlassbereich, Dämpfung im Sperrbereich monoton verlaufend | Gute Flankensteilheit im Durchlassbereich | Große Änderung der Gruppenlaufzeit, schlechtes Zeitverhalten |
| Inverse Tschebyscheff-Filter | Monotoner Verlauf im Durchlassbereich, Welligkeit im Sperrbereich | Gute Flankensteilheit im Durchlassbereich | Große Änderung der Gruppenlaufzeit, schlechtes Zeitverhalten |
| Bessel-Filter auch als Thomson-Filter bezeichnet |
Impulsformung | Konstante Gruppenlaufzeit (=lineare Phase) im Durchlassbereich | Geringe Flankensteilheit im Übergangsbereich |
| Cauer-Filter auch als elliptisches Filter bezeichnet |
Welligkeit im Durchlass- und Sperrbereich | Sehr gute Flankensteilheit im Übergangsbereich | Große Änderung der Gruppenlaufzeit, schlechtes Zeitverhalten |
| Gauß-Filter | Impulsformung | Konstante Gruppenlaufzeit im Durchlass- und Sperrbereich. Kein Überschwingen bei der Sprungantwort. Reduzierte Intersymbolinterferenz | Geringe Flankensteilheit im Übergangsbereich |
| Raised-Cosine-Filter | Impulsformung, Nyquist-Filter | Keine Intersymbolinterferenz | Geringe Flankensteilheit im Übergangsbereich |
| TBT-Filter Transitional-Butterworth-Thomson-Filter |
Impulsformung | Einheitssprungantwort zwischen Butterworth- und Thomson-Verhalten | Mehr Überschwinger als Thomson-Filter |
Adaptive Filter
[Bearbeiten | Quelltext bearbeiten]Normale Filter haben eine fest eingestellte Kennfrequenz fc (beispielsweise um Störungen durch die Netzfrequenz 50 Hz oder deren Vielfache zu eliminieren). Wenn die Störung in der Frequenz variiert, können zur Verbesserung des Signal/Rauschverhältnisses adaptive Filter eingesetzt werden.
Übertragungsfunktionen digitaler Filter
[Bearbeiten | Quelltext bearbeiten]Diese primär bei analogen Filterstrukturen angewendeten Übertragungsfunktionen können, mit kleineren Anpassungen, auch auf digitale Filter in der Struktur von IIR-Filtern übertragen werden. Die Anpassungen betreffen dabei den wesentlichen Umstand, dass digitale Filter mit zeitlich diskreten Werten und somit einer endlichen Basisbandbreite arbeiten.
Übertragungsfunktionen nicht kausaler Filter
[Bearbeiten | Quelltext bearbeiten]Daneben können weitere Übertragungsfunktionen eingesetzt werden, welche je nach Anwendung entsprechend ausgelegt sind.
Deren Übertragungsfunktion ist nicht kausal. Sie folgen einer finalen Gesetzmäßigkeit, welche nicht nur Augenblickswerte, sondern auch deren Verlauf berücksichtigt. Die Übertragungsfunktion spielt wegen ihres einfachen Aufbaus und Modellcharakters in der Filtertheorie eine wesentliche Rolle. Einfachste Beispiele sind theoretische Übertragungsfunktionen, welche sich praktisch nicht realisieren lassen, wie die des idealen Tiefpasses.
Ordnung
[Bearbeiten | Quelltext bearbeiten]Die Ordnung eines Filters beschreibt die Verstärkungsabnahme (Dämpfung und Flankensteilheit) von Frequenzen (weit) oberhalb oder unterhalb der jeweiligen Grenzfrequenz des Filters. Sie ist bei Tiefpass- oder Hochpassfilter über der Frequenz etwa n · 6 dB pro Oktave (n · 20 dB pro Dekade), wobei n die Ordnung des Filters darstellt. Für Bandpässe bzw. Bandsperren, welche Kombinationen aus Tiefpass- und Hochpassfiltern darstellen und somit zwei Filterflanken aufweisen, ist die Filterordnung als Funktion der Steilheit der Filterflanke doppelt so hoch: Ein Bandpass 4. Ordnung weist mitunter 40 dB pro Dekade auf. Maßgeblich ist die Filtergüte Q.
Filter höherer Ordnung können entweder durch Hintereinanderschaltung von Filtern niedriger Ordnung (1. und 2. Ordnung) realisiert oder durch entsprechende Schaltungen[2] erstellt werden.
Die Übertragungsfunktion lautet:
mit
- Gleichspannungsverstärkung
- Filterkoeffizienten
- mit als Grenzfrequenz
- n Ordnung des Filters
Filtertypen
[Bearbeiten | Quelltext bearbeiten]Filter und Frequenzgang, Selektionsverhalten
[Bearbeiten | Quelltext bearbeiten]
Die theoretischen Standardfälle des Selektionsverhaltens eines Filters sind:
- Ein Tiefpassfilter schwächt die hohen Frequenzen bis zu einer Grenzfrequenz und lässt alle tieferen Frequenzen praktisch ohne Abschwächung (Verstärkung = 1) passieren. Anwendung findet dieser „Tiefpass“ zum Beispiel als Anti-Aliasing-Filter (siehe Alias-Effekt) oder zur Rauschunterdrückung.
- Ein Hochpassfilter schwächt die tiefen Frequenzen bis zu einer Grenzfrequenz, während alle höheren Frequenzen (mit der Verstärkung 1) durchgelassen werden. Mit diesem „Hochpass“ lassen sich unter anderem Gleichspannungsanteile oder langsames Driften im Signal unterdrücken.
- Ein Bandpassfilter schwächt alle Frequenzen außerhalb eines Frequenzintervalls ab, das durch zwei Grenzfrequenzen festgelegt ist. Amplituden- oder frequenzmodulierte Signale tragen den Hauptanteil ihrer Information in einem begrenzten Frequenzband. Ein Bandpass lässt diesen Anteil aus Frequenzgemischen passieren und sperrt die Anteile unterhalb und oberhalb der Grenzfrequenzen. Bandpassfilter werden auch kurz Bandfilter genannt und zum Beispiel im Hochfrequenzbereich eines Superhet-Rundfunkempfängers zur Frequenzselektion der Zwischenfrequenz verwendet.
- Ein Bandstoppfilter (Saugkreis, Kerbfilter, Bandsperre) stellt die Umkehrung des Bandpassfilters dar. Nur Frequenzen innerhalb eines Frequenzintervalls, das durch zwei Grenzfrequenzen festgelegt ist, werden abgeschwächt. Störungen fester Frequenz, wie die Störungen der Netzfrequenz oder die Einstrahlung von Rundfunksendern, lassen sich aus dem Signal mehr oder weniger wirkungsvoll entfernen.
- Ein Allpassfilter lässt alle Frequenzen bei gleicher Verstärkung zum Ausgang durch. Mit Allpässen kann eine frequenzabhängige Phasenverschiebung oder eine Impedanztransformation durchgeführt werden.
- Ein Multiratenfilter (wie zum Beispiel CIC-Filter) wird in der digitalen Signalverarbeitung zur Konvertierung von Signalfolgen zwischen unterschiedlichen Abtastraten verwendet. Es dient zur Unterdrückung von Aliasing und zur Vermeidung von Spiegelspektren.
Der Idealfall einer rechteckigen bzw. stufenförmigen Übertragungsfunktion lässt sich in der Praxis allerdings nicht erreichen. Im Rahmen des Filterentwurfes zur Bestimmung der Filterparameter wird üblicherweise von einem normierten Tiefpassfilter ausgegangen. In Folge werden die ermittelten Filterkoeffizienten mittels Filter-Transformationen wie der Tiefpass-Hochpass-Transformation oder einer Tiefpass-Bandpass-Transformation auf die eigentliche Filterart des Zielsystems umgesetzt.
Entsprechende Filterarten werden sowohl im Niederfrequenzbereich (zum Beispiel Audiotechnik) als auch im Hochfrequenzbereich (zum Beispiel Rundfunktechnik) verwendet.
Parametrische Filter sind in einem oder mehreren Parametern (Frequenz, Güte) einstellbar und können meistens wahlweise als Tiefpass-, Hochpass- oder Bandpassfilter betrieben werden. Einsatzgebiete sind Mischpulte und Audiotechnik.
Lineare und nichtlineare Filter
[Bearbeiten | Quelltext bearbeiten]Lineare Filter
[Bearbeiten | Quelltext bearbeiten]Bei einem linearen Filter sind die Eigenschaften der Filterung unabhängig vom Signalpegel. Das Signal wird nicht verzerrt. Wenn man das Eingangssignal für eine bestimmte Frequenz um einen Faktor a vergrößert, so ist auch das Ausgangssignal für diese Frequenz entsprechend vergrößert. Die Form des Signals wird dabei nicht grundlegend verändert. Tiefpass, Hochpass, Bandpass, Bandsperre und Allpass werden als lineare Filter bezeichnet. Es gibt aber auch wesentlich komplexere lineare Filter. Beispielsweise ist ein Echo-Effekt oder ein Kammfilter ebenfalls linear.
Sie können als Vierpolersatzschaltbild dargestellt werden.
Der Begriff linearer Filter wird in der Regel als Synonym für einen linear zeitinvarianten Filter verwendet.
Nichtlineare Filter
[Bearbeiten | Quelltext bearbeiten]Bei einem nichtlinearen Filter sind die Eigenschaften der Filterung abhängig vom Signalpegel und vom zeitlichen Verlauf des Signals. Das Signal wird in seiner Form verzerrt. Zu den nichtlinearen Filtern gehören zum Beispiel Begrenzer, Verzerrer, Gleichrichter (Betrag) und Medianfilter.
Passive und aktive Filter
[Bearbeiten | Quelltext bearbeiten]Passive Filter
[Bearbeiten | Quelltext bearbeiten]Passive Filter basieren auf Kombinationen von Widerständen (R), Spulen (L), Kondensatoren (C) oder zum Beispiel Quarzen (Q) oder Keramikelementen. Damit sind zum Beispiel Filter aus RC-, RL-, LC-, LCQ oder RCL-Kombinationen realisierbar.
Da diese Filter ohne externe Spannungsversorgung arbeiten können, werden diese Kombinationen „passive Filter“ genannt. Je nach Aufbau des Netzwerkes wirken die Filter als Tiefpass-, Bandpass-, Hochpass-, Bandstopp- oder als Allpassfilter.
In den vielen Filteranwendungen ist ein scharfer Übergang der Übertragungsfunktion vom Durchlass- in den Sperrbereich erwünscht. Die „Schärfe“ wird durch den Gütefaktor Q des Filters angegeben. Je größer die Güte, desto größer ist die Dämpfung im Sperrbereich pro Dekade. Der Grad und Art der Übertragungsfunktion, und damit auch die Anzahl und Qualität der Bauelemente des Filters, sowie die Kosten für die Realisierung, richten sich nach der gewünschten Güte.
Passive Filter werden oft nach der Art ihrer Übertragungsfunktion bezeichnet, zum Beispiel Bessel-, Tschebyscheff-, Cauer-Filter. Sie eignen sich besonders gut für Filteraufgaben im Bereich hoher Frequenzen und hoher Leistungen sowie in allen Anwendungsfällen, bei denen es auf geringes Eigenrauschen und hohe Linearität ankommt. Eine Sonderform von passiven Filtern stellen die mit Hohlleitern realisierten Hohlleiterfilter dar, da dabei keine diskreten Bauelemente eingesetzt werden, sondern sich die Filtereigenschaft durch die Geometrie des Aufbaues ergibt.
Beispiele für die Anwendung von passiven Filtern sind:
- PLC-Filter in Hochspannungsleitungen
- Saugkreis
- Zwischenkreis
- Oberschwingungsfilter
- Netzfilter
Aktive Filter oder elektronische Filter
[Bearbeiten | Quelltext bearbeiten]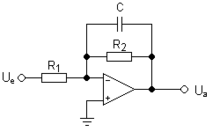
Aktive Filter bestehen neben den passiven Komponenten noch aus aktiven Komponenten wie zum Beispiel Transistoren oder Operationsverstärkern (OPV). Damit benötigen aktive Filter stets eine eigene Spannungsversorgung. Bei der Realisierung aktiver Filter werden als passive Komponenten häufig nur noch Widerstände (R) und Kondensatoren (C) eingesetzt. In diesem Fall wird ein solcher Filter auch aktiver RC-Filter genannt. Ein besonders einfacher aktiver RC-Filter zweiter Ordnung wird als Sallen-Key-Filter bezeichnet.
Mit aktiven RC-Filtern können Induktivitäten simuliert werden (Gyrator), wodurch gerade bei kleinen Frequenzen (< 1 kHz) auf große Spulen verzichtet werden kann.
Zusätzlich erlauben die aktiven Komponenten eine Verstärkung des Signales, sodass aktive Filter zugleich auch Verstärker darstellen können.
Analoge Filter
[Bearbeiten | Quelltext bearbeiten]Ein Filter wird als analoges Filter bezeichnet, wenn es die Signale zeit- und amplitudenkontinuierlich verarbeitet.
Digitale Filter und digitale Signalprozessoren (DSP)
[Bearbeiten | Quelltext bearbeiten]
Die digitalen Filter lassen sich nach der Art des Eingang- bzw. Ausgangssignales einteilen; berücksichtigt wird, ob diese analog oder digital vorliegen und weiterbearbeitet werden. Im ersten Fall muss das Eingangssignal über einen A/D-Wandler digitalisiert werden, bevor es bearbeitet werden kann. Nach der Bearbeitung muss das Signal mit Hilfe eines D/A-Wandler wieder umgesetzt werden.
Durch die Bearbeitung von digitalisierten Signalen entweder mit Signalprozessoren oder mit Computern wird eine Flexibilität erreicht, die von keinem anderen Filtertyp erreicht werden kann. Die Flexibilität liegt darin, dass das Filter durch einen Datensatz modelliert wird, der relativ einfach geändert werden kann. So können mit einem Filter alle oben genannten Filtertypen realisiert werden, ohne dass Änderungen an der Hardware vorgenommen werden müssen.
Die oft als Nachteil angeführte Latenzzeit, welche durch die AD- und DA-Wandlung verursacht wird, kann mittlerweile vernachlässigt werden, da sie bei üblichen Wandlern nur noch wenige Samples beträgt. Durch die Verwendung einer höheren Abtastrate (96 kHz) kann diese noch einmal verkürzt werden, da zum Beispiel bei DA-Wandlern ein Tiefpassfilter mit einer geringeren Steilheit zugunsten einer geringeren Latenz gewählt werden kann.
Digitale Filter können das Signal entweder im Zeitbereich bearbeiten (analog zu den anderen Filterarten) oder im Frequenzbereich.
Im Zeitbereich liegt der Vorteil der digitalen Filter in der nicht vorhandenen Bauteiltoleranz und Alterung der Bauteile.
Im Frequenzbereich können die Filter sehr flexibel gestaltet werden, insbesondere können diese Filter deutlich leichter den vorhandenen Gegebenheiten angepasst werden, da das Filter als Datensatz vorliegt.
Die Transformation zwischen dem Zeitbereich und dem Frequenzbereich (und umgekehrt) kann unter anderem mit der Fourier- oder Laplace-Transformation durchgeführt werden.
Anwendung finden digitale Filter zum Beispiel in
- Audiotechnik (zum Beispiel mit echtzeitfähigem DSP) als Effektgerät
- Videotechnik
- Funktechnik
Weiterhin kann jede Prozedur, die einem digitalen oder analogen Eingangssignal reproduzierbar ein definiertes Ausgangssignal zuordnet, als digitaler Filter verstanden werden, zum Beispiel Chiffren oder die Filterfunktionen in Audioprogrammen oder Bildbearbeitungsprogrammen.
Mit digitalen Filtern können Signale außer in Echtzeit auch zeitlich unabhängig von ihrer Verwendung berechnet werden. Zum Beispiel ist es möglich, sehr komplexe Bearbeitungen anzuwenden, um alte Schallplattenaufnahmen zu restaurieren.
Durch Faltung können einem Tonsignal Klangcharakteristiken komplexer Umgebungen aufgeprägt werden.
Siehe auch: Filter mit endlicher Impulsantwort
Andere Filter
[Bearbeiten | Quelltext bearbeiten]- Quarzfilter
- In den 1930er Jahren stellten Ingenieure fest, dass verschiedene Schwingquarze bei akustischen Frequenzen mitschwingen können. Heutzutage werden Quarze vor allem bei wesentlich höheren Frequenzen eingesetzt. Der Vorteil von Quarz gegenüber anderen harten Materialien ist der piezoelektrische Effekt, der es ermöglichte, direkt die mechanische Schwingung in elektrische umzuwandeln und umgekehrt, sie stellen daher eine Bauform eines mechanischen Filters dar. Weiterhin besitzen Quarze eine geringe thermische Ausdehnung, so dass die Frequenz über einen großen Temperaturbereich konstant bleibt. Quarzfilter besitzen eine wesentlich höhere Güte als LCR-Glieder. Wenn eine noch höhere Güte benötigt wird, können die Quarze zusätzlich temperaturstabilisiert oder auch hintereinander geschaltet werden.
- Keramikfilter
- Das Funktionsprinzip der Keramikfilter, auch dielektrische Filter genannt, gleicht dem der Quarzfilter und bestehen aus spezieller Keramik; Wie die Quarzfilter sind auch sie eine Bauform von mechanischen Filtern. Sie haben schlechtere technische Eigenschaften, sind dafür weitaus kostengünstiger herstellbar. Sie werden vorwiegend im Zwischenfrequenzbereich von analogen Funkempfängern eingesetzt.
- YIG-Filter
- Sind durch ein Magnetfeld einstellbare Filter für Mikrowellen im Bereich einiger GHz.
- Atom-Filter
- Um Filter bei sehr hohen Frequenzen zu realisieren, können die Eigenschwingungen von Atomen und Molekülen ausgenutzt werden. Dieses wird zum Beispiel bei der Atomuhr verwendet. Diese Filter besitzen extrem hohe Gütefaktoren.
- Switched-Capacitor-Filter
- Bei dem Switched-Capacitor-Filter werden mehrere Kondensatoren durch elektronische Schalter verbunden und bilden zusammen mit Widerständen ein Schaltnetz. Die Taktfrequenz, mit der die Schalter geschaltet werden, hat direkten Einfluss auf den Frequenzgang. Sie muss deutlich höher als die höchste zu filternde Frequenz liegen.
- AOW-Filter / SAW-Filter
- Akustische-Oberflächenwellen-Filter, auch AOW- oder SAW-Filter genannt, basieren auf der Interferenz von Signalen verschiedener Laufzeit, realisiert mit dem Piezoeffekt. Es sind hohe Güten erreichbar; Ausführung meist als Bandpassfilter mit einer geringen Bandbreite von wenigen MHz und finden deshalb vor allem in der mobilen Datenübertragung Anwendung.
- BAW-Filter
- BAW-Filter (englisch bulk acoustic wave) sind ebenfalls auf dem Piezoeffekt beruhende Filter, die auf CMOS-Basis hergestellt werden und gegenüber den SAW-Filtern entscheidende elektrische und physikalische Vorteile bietet.
- Raised-Cosine-Filter
- Raised-Cosine-Filter sind realisierbare Impulsformfilter mit flacher Flanke, die die erste Nyquistbedingung erfüllen und keine Intersymbolinterferenz (ISI) erzeugen.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Duden: Filter
- ↑ Gottfried Fritzsche, Volkmar Seidel: Aktive RC-Schaltungen in der Elektronik. Hüthig Verlag, Heidelberg 1981, ISBN 3-7785-0733-8.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Karl-Dirk Kammeyer: Nachrichtenübertragung. 4., neu bearbeitete und ergänzte Auflage. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8351-0179-1.
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. Filterung und Spektralanalyse. 7., erweiterte und korrigierte Auflage. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8348-0610-9.
- Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 8. Auflage. Springer-Verlag, 1986, ISBN 3-540-16720-X (mit ausführlichen Tabellen für die Filterkoeffizienten von kaskadierten Sallen-Key-Filtern bis zur 10. Ordnung)
- Adel S. Sedra, Peter O. Bracket: Filter Theory and Design: Active and Passive. Matrix Publishers, Beaverton, Oregon 1978, ISBN 0-916460-14-2.
![{\displaystyle A[P]={\frac {A_{0}}{\sum _{i=0}^{n}c_{i}P^{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/073ac4d47ca8dc9852bd67a00937efa7da24ace9)



